№59 (Воскресная заминка в воскресенье)

Предлагается завершить неделю следующей нетрудной задачей

O и H - центр описанной окружности и ортоцентр треугольника ABC соответственно. Угол A = 120 градусов.
Доказать, что OH = АВ + АC
(На картинке опечатка, отмечены не те отрезки)

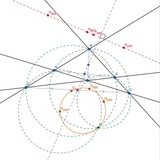
№60 (ВсОШ РЭ 2025, 11.5)

Треугольник ABC вписан в окружность Ω. Пусть прямые AD, BE и CF - его высоты, а точки M, N и P - середины сторон BC, AC и AB соответственно. Прямые AM, BN и CP пересекают описанную окружность треугольника DEF в точках I, J и K соответственно. Описанные окружности треугольников AID, BJE и CKF пересекают Ω в точках X, Y и Z, соответственно. Точки А', B' и C' - отражения точек X, Y, Z соответственно относительно M, N и P соответственно.
Доказать, что прямые AA', BB', CC' пересекаются в одной точке

Сори, перепутал

№61 (SteelBrawl Shop)

Дан остроугольный треугольник ABC. Высоты, проведенные из точек A и B, пересекаются в точке H и пересекают внешнюю биссектрису угла C в точках Y и X соответственно. Внешняя биссектриса угла AHB пересекает отрезки AX и BY в точках P и Q соответственно.
Доказать, что если PX = QY, то
AP + BQ >= 2CH.

Отдам канал в хорошие (или не очень) руки

Милая полуночная задачка. Авторство приписывают легендарному TelvCohl-ю.

Соответствующие пары точек изогонально сопряжены в треугольнике ABC, красные векторы равны. Докажите, что P — ортоцентр треугольника P_1P_2P_3.

И вдогонку пара интересных вопросов:
а) Пусть красный вектор фиксирован. Как построить чертёж к задаче в геогебре?
б) Можно ли обойтись циркулем и линейкой?

Шокирующие новости! На канале «Geometry Weekly» вышли две задачи за неделю — непорядок.

Точка G — центроид треугольника ABC. Докажите, что точки Лемуана треугольников ABC и A’B’C’ совпадают.

Да, задачу несложно посчитать в векторах/барицентрических. Но интересно подумать и над геометрическими решениями. Самое короткое из известных мне занимает, если немного слукавить, полторы строчки

Задачка попробще. Может, баян

Когда я узнал этот факт несколько лет назад, то сильно удивился. Не существованию, а тому, что не замечал его раньше — настолько классическим он выглядит

P.S. Когда-нибудь я разберусь, как писать сообщения от имени сообщества, и смогу разговаривать с подписчиками

Задача Николая Белухова из журнала KöMaL:

Четырёхугольник ABCD описан вокруг окружности ω. Окружность γ проходит через точки A, C и касается ω в точке P. Общая касательная к ω и γ в точке P пересекает диагональ BD в точке Q. Докажите, что вторая касательная из Q к ω параллельна AC.

Очередной отмыв денег в «ЛУЧШЕМ» техническом университете страны. Спонсирование лудомании под видом благой цели.

— Распоряжение бюджетом. построить 5этажный многоквартирный дом (считайте новую общагу лфишникам) стоит 150кк
платить стобалльникам 100к в 2024 + 200к в 2025 стоит 150кк.

— Инвестиция в таланты. Участник всероса << 100 баллов егэ < призёр всероса << двухстобальнтк ЕГЭ. Да даже так: возьмем человека, который написал профмат на 99 баллов в первую волну и человека, набравшего 80 в основную и 100 на пересдаче в 2025.

— НЕблагая цель. сообщение о выплатах вышло поздно, а значит не было цели популяризировать технические специальности в РФ. К тому же никогда не было избытка свободных мест на физтехе для егэшников. Гораздо лучше было бы провести такую акцию в МГТУ или МИФИ

— Гадость для страны. 100 балльник с баллом 306 переносить документы из бауманки в физтех, надеясь пройти по конкурсу и главное получить 200к. Однако все места на физтехе разобраны бвишниками. И в итоге чел вообще никуда не попал и пролетел даже на первоначальную техническую специальность. Итог: нехватка кадров

— Пропаганда списывания.
Очередной повод списать экзамен. Списать ЕГЭ теперь будут хотеть даже олимпиадники, которым к тому же нечего терять в вопросе поступления.

Таким образом, возможно:
1) на физтехе не умеют распоряжаться бюджетом. Гораздо лучше для страны было бы отправить эти деньги на СВО.
2) Банальный отмыв денег. Уже недавно всплывала новость о коррупции в данном заведении.

Наверное, стоит обратить больше внимание на МИФИ, который к тому же напрямую сотрудничает с Росатомом. Они активно развивают сейчас и IT проекты. А вот буквально несколько часов назад всплыла новость:

В МИФИ подготовят кадры для цифровой экономики РФ, фундаментом проекта станет Wildberries

Я лично сам пойду и перенесу документы с загнивающего Физтеха в расцветающий МИФИ. Советую другим олимпиадникам тоже об этом задуматься, к тому же в мифи их ценят и любят, обзванивают абитуриентов и желают успехов в поступлении, не навязывая выбор.

Я, автор канала PhysicsWeekly уже отправил претензию Мизулиной. Призываю и вас. Распространите.

Думайте.

Physics Weekly. Подписаться

Перевод названия Леммы Рыжик сделал сам. Может у вас получится лучше?

Встречайте новую лемму ARL🔥
Подробно о ней можно будет узнать на научной конференции https://turgor.ru/lktg/

Можно также задать вопросы Юсуфу и Станиславу под этим постом.
Ну а Рыжик пошел отдыхать😻

Этот ролик уже в YouTube https://youtube.com/shorts/4LCis0kBqV4?si=6IGi0LNmemEkdI6J

(Шарыгинская олимпиада 2025, 10.4)

H - ортоцентр серого треугольника
Доказать, что красная прямая проходит через H

Ой простите, я перепутал задачи. Это высшая проба 2026 11.6.

(Задача с aops…🥀🥀🥀)

M - середина BC, A’ - симметрия A относительно DE
Доказать, что DE, IO и A’M пересекаются в одной точке

Какие же вы слабые... Никто даже НЕ ПОПЫТАЛСЯ решить... И. Ф. Шарыгин как-то сказал, что геометрия - это искусство решать ВЕРНУЮ задачу на НЕВЕРНОМ чертеже. Как будто впервые видите рисунок, где прямые, которые должны пересекаться в одной точке, не пересекаются. Это многое говорит о вас...