Нарушение критерия сверхтекучести Ландау не обязательно означает реальное исчезновение сверхтекучести. Формально при сверхкритической скорости потока энергии некоторых боголюбовских возбуждений становятся отрицательными, и это приводит к затуханию сверхтекучего потока за счет их массового возбуждения.

Однако в случае сверхтекучих ферми-систем – таких как купратные сверхпроводники или гелий-3 – боголюбовские возбуждения могут просто заполнить те области импульсного пространства, где их энергии отрицательны. Они образуют свои поверхности Ферми и на этом все закончится. Как результат, из-за нарушения критерия Ландау сверхтекучая плотность уменьшается, но не до нуля.

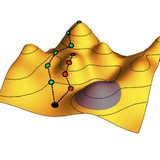
А в этой статье предложено погрузить в сверхтекучий гелий-3 решетку цилиндриков, из-за которой поверхность Ферми боголюбовских возбуждений примет форму, показанную на рисунке. При этом в некоторых местах (в окрестностях точек вырождения) боголюбовские возбуждения будут вести себя как электроны в вейлевских полуметаллах.

#сверхтекучесть

Наполовину обзор, наполовину педагогическое введение в физику неэрмитовых топологических состояний Флоке-Блоха. Это периодические в пространстве системы, которые подвергаются периодическим во времени возмущениям, обладают неэрмитовыми гамильтонианами и, вдобавок, демонстрируют нетривиальную топологию квантовых состояний.

Как показано на рисунке, здесь совмещаются сразу три популярные темы – открытые системы, состояния Флоке и топология. Из-за периодического внешнего воздействия нужно смотреть не на энергии частиц, а на их квазиэнергии, заполняющие зону Флоке – аналог периодически повторяющейся первой зоны Бриллюэна.

Классификация топологических фаз получается здесь довольно сложной, поскольку энергии, вообще говоря, являются комплексными. Из-за неэрмитовости важную роль играют исключительные точки, в которых происходит бифуркация энергий, а периодичность зоны Флоке дает возможность возникать новым видам зонных структур и краевых состояний.

#неэрмитовы_системы #топологические_материалы

А вот пример из обзора из предыдущего поста, иллюстрирующий запутанную структуру топологически нетривиальных состояний в неэрмитовых флоке-системах.

Это относительно простая модель одномерной цепочки, для которой на верхней и нижней строках графиков показаны спектры, соответственно, вещественных и мнимых частей квазиэнергии. Посчитаны они в зависимости от величины асимметрии двух подрешеток μ при слабой (левый столбец) и сильной (правый столбец) неэрмитовости.

Серые линии показывают энергии цепочки при периодических граничных условиях. Видно, что при этом энергии всегда комплексны, а на оси Re E имеются две энергетические зоны, щель между которыми может закрываться. Синие линии отвечают цепочке с открытыми граничными условиями. В этом случае энергии иногда полностью вещественны, это проявление неэрмитового скин-эффекта. Желтые круги показывают величину топологического инварианта, а красные линии указывают на краевые состояния.

#неэрмитовы_системы #топологические_материалы

Визуализация плазмонных резонансных мод на серебряном квадрате размером 850 нм при различных энергиях.

Любопытно, что вначале плазмонные моды сосредоточены преимущественно на краях, то есть являются одномерными стоячими волнами. Но затем, по мере роста энергии, они сменяются модами толщи, то есть двумерными стоячими волнами на квадрате.

https://www.youtube.com/watch?v=rnfCdhTZbJQ

#плазмоны

Связанные состояния двух притягивающихся частиц стабильны потому, что им некуда распадаться: их полная энергия опускается ниже края континуума, где отсутствуют другие состояния, в которые можно было бы перейти с сохранением энергии. Но этот же принцип можно и перевернуть: две отталкивающиеся частицы могут образовать стабильное связанное состояние, если его энергия находится выше континуума свободного движения. Для этого он должен быть ограничен сверху, что в кристаллах – обычное дело.

В модели Хаббарда энергия такого «связанного» состояния с двумя частицами в одной ячейке порядка силы отталкивания на узле U. А ширина континуума – то есть энергетической зоны кристалла – задается интегралом перескока J. При U >> J связанному состоянию некуда распадаться с сохранением энергии (если нет диссипации). Это подтверждается графиком снизу, где, как функции суммарного импульса K, посчитаны энергии связанного (черная кривая) и свободных (серый континуум) двухчастичных состояний.

#квантовая_механика #отвал_башки

Представим себе мир, в котором нет квантовых когерентностей – то есть матрицы плотности всех систем диагональны в базисе собственных векторов своих гамильтонианов. Такой мир будет застывшим и в нем будет невозможно отсчитывать время, поскольку для такого отсчета нужны осцилляции вида exp{i(E₁–E₂)t/ℏ}, возникающие только при наличии квантовых суперпозиций состояний с энергиями E₁ и E₂. Можно сказать, что наличие квантовой когерентности создает точку отсчета, нарушающую симметрию по отношению к сдвигам во времени и, тем самым, позволяющую его измерять.

Таким образом, квантовая когерентность – это важный ресурс. Он необходим не только для отсчитывания времени, но и для реализации любых когерентных операций, то есть операций, не коммутирующих с гамильтонианом и позволяющих создавать суперпозиции его собственных векторов. Пример такой операции – это преобразование Адамара, поворачивающее блоховский вектор кубита на угол π/2 и превращающее состояние |0> в суперпозицию (|0>+|1>)/√2. Реализовать его можно, в частности, облучая кубит лазерным импульсом определенной длительности, и здесь источником когерентности является когерентное состояние лазерного света – суперпозиция фоковских состояний |n> с различными числами фотонов.

Как любой ценный ресурс, когерентность может быть использована для чего-то полезного, а может быть растрачена напрасно. В любом случае, в мире диагональных матриц плотности количество имеющейся у нас когерентности не может возрастать – если только у нас нет какого-то внешнего источника такого ресурса. А в этой работе показано, что с когерентностью, в принципе, можно обращаться очень осторожно, используя ее как катализатор – ресурс, который многократно используется, но не тратится в процессе.

Автор показал, что при наличии резервуара, обладающего квантовой когерентностью (недиагональными элементами матрицы плотности), можно совершать над имеющимся у нас кубитом любые унитарные операции, в том числе когерентные. После каждой такой унитарной операции матрица плотности резервуара изменяется, но его ресурсность – способность помогать нам в совершении когерентных операций – остается прежней.

Хотя здесь имеется тонкость: состояние резервуара деградирует в том смысле, что его матрица плотности после каждого использования должна разбрасываться по все большему числу уровней энергии. К примеру, если до использования были населены уровни с номерами от n₁ до n₂, то после использования будут населены уровни с n₁–1 по n₂+1. Поскольку уровни энергии ограничены снизу, нам нужно каждый раз «регенерировать» резервуар, поднимая его как целое на один уровень энергии, чтобы в конце этого были населены уровни с n₁ по n₂+2. Для такой регенерации нужно тратить дополнительную энергию (но не когерентность).

Тем не менее, на практике возможность нарастания разброса энергии резервуара также будет ограничена, так что квантовая когерентность как катализатор может иметь хоть и долгий, но ограниченный срок службы.

#квантовая_механика #квантовая_термодинамика

Разложение электромагнитного поля по полному набору нормальных мод – собственных решений уравнений Максвелла в заданной геометрии – не всегда возможно и практично, особенно при наличии диссипации и дисперсии отклика среды.

Здесь на помощь приходят так называемые квазинормальные моды – это несколько решений уравнений Максвелла, отвечающие самым важным в контексте задачи резонансам и обладающие комплексными частотами (то есть затухающие). Они не образуют полного базиса, так что часть электромагнитного поля, не разложенная по квазинормальным модам, рассматривается как нерезонансный фон.

В этой статье дается практический рецепт численного разложения поля на квазинормальные моды и нерезонансный фон. Он основан на том, что поле при интересующей нас вещественной частоте ω (любая из черных точек на диаграмме снизу) представляется в виде интеграла Коши по комплексной плоскости ω. Вклады полюсов (крестики) отвечают квазинормальным модам, а оставшийся интеграл (по синему контуру) дает нерезонансный фон.

#фотоника

А вот пример разложения электромагнитного поля по квазинормальным модам из статьи из предыдущего поста. Дипольный источник излучения слегка погружен в цилиндр из алмаза, диэлектрическая функция которого описывается моделью Лоренца с двумя затухающими резонансами в УФ-диапазоне.

Панель (b) показывает полное электромагнитное поле, образуемое дипольным источником на одной из частот – видно, что там велик вклад вертикальной дипольной моды. А на панелях (c), (d), (e) показаны поля трех квазинормальных мод, найденные как собственные решения уравнений Максвелла с комплексными частотами.

При помощи интегрирования по комплексной плоскости поле можно разложить на сумму вкладов трех квазинормальных мод (с амплитудами, зависящими от частоты колебаний диполя ω) и оставшегося нерезонансного фона. Это позволяет посчитать, например, скорости передачи энергии от диполя к каждой моде. Их зависимости от ω, имеющие форму уширенных резонансов (что свидетельствует об эффекте Пёрселла), показаны на графике снизу.

#фотоника

В этой работе предложена концепция «фотонного холодильника» с интересным принципом работы.

Берем две фотонные моды с частотами ω₁ и ω₂. При этом мода меньшей частоты (ω₁) связана с холодным резервуаром, имеющим температуру T_c, а мода большей частоты (ω₂) связана с горячим резервуаром, имеющим температуру T_h. Вдобавок, сила взаимодействия между двумя модами модулируется с течением времени с резонансной частотой ω₂–ω₁. Ключевой момент здесь в том, что такое взаимодействие не сохраняет энергию системы – для создания внешней модуляции нужно совершать работу – но сохраняет суммарное число фотонов в обеих модах.

Авторы показывают, что при T_c/ω₁ > T_h/ω₂ система работает как холодильник, перекачивая энергию из холодного резервуара в горячий через обе моды. Это происходит, потому что фотонная населенность T_c/ω₁ первой моды превышает населенность T_h/ω₂ второй моды, так что фотонам выгоднее переходить из первой моды во вторую, хотя взаимодействие между ними полностью симметрично.

#квантовая_термодинамика

Статья из предыдущего поста удостоилась отдельной заметки в Physics Magazine на сайте Американского физического общества. И к ней приложили вот такую иллюстрацию, которая, по-видимому, должна понятным для читателей образом описывать идею фотонного холодильника.

Квантовый геометрический тензор η в кристалле определяется как скалярное произведение волновых функций при исходном k и слегка сдвинутом k+dk квазиимпульсах. Его можно разделить как η = g + iΩ, на симметричную вещественную часть g (квантовый метрический тензор, или метрика Фубини-Штуди) и антисимметричную мнимую часть Ω (тензор кривизны Берри).

Интуитивно понятно, что кривизна Ω приводит к дополнительному растяжению метрики g, помимо уже имеющегося. Двумерные материалы, в которых кривизна Берри является единственным источником неоднородной метрики, называются идеальными изоляторами Черна. Оказывается, что энергетическая зона идеального изолятора Черна эквивалентна, с точностью до калибровочного преобразования, уровню Ландау n=0, образующемуся в пространственно периодическом магнитном поле. Плоская же по энергии энергетическая зона эквивалентна случаю, в котором вариации энергии из-за неоднородности магнитного поля компенсируются периодическим потенциалом.

#уровни_Ландау #топологические_материалы

Обзор, посвященный перспективам создания электронных и оптоэлектронных устройств на основе ван-дер-ваальсовых гетероструктур, состоящих из проводящего графена, изолирующего нитрида бора, полупроводниковых дихалькогенидов переходных металлов и т.д. Устройства, интересные с прикладной точки зрения – это транзисторы, диоды, светодиоды, фотодиоды и солнечные батареи.

Главное новшество, предлагаемое гетероструктурами из двумерных материалов – это возможность создания устройств вертикальной геометрии, где мы управляем протеканием электрического тока не по горизонтали (например, вдоль канала полевого транзистора), как обычно происходит при современной планарной технологии создания интегральных схем, а по вертикали – путем туннелирования между различными слоями.

На рисунке схематически показано, чем отличаются горизонтальный транзистор от вертикального. Пока что главная техническая проблема подобных устройств – это барьеры Шоттки, возникающие на контактах с металлами.

#дихалькогениды_переходных_металлов #графен

А вот какая многослойная структура была изготовлена в этой работе и служит светодиодом, где электрон и дырки, в ходе вертикального туннелирования, рекомбинируют с испусканием фотонов.

Большое число слоев здесь нужно, чтобы электроны не туннелировали сразу через всю структуру, закорачивая ее и напрасно растрачивая электрический ток. Квантовая эффективность получившегося устройства составляет 10% – она почти достигает показателей современных полупроводниковых светодиодов.

Интересно также, что эта структура почти прозрачна и может быть нанесена на гибкую подложку.

#дихалькогениды_переходных_металлов #фотоника

Из-за продольно-поперечного расщепления на экситонные поляритоны в микрополости действует эффективное псевдомагнитное поле, вращающее их поляризацию. Это поле по модулю пропорционально квадрату импульса поляритона и совершает два оборота при обходе импульса вокруг начала координат. Однако оно не является калибровочным полем, поскольку не входит в гамильтониан посредством минимальной подстановки p → p – A.

В этой статье рассмотрели, что будет при одновременном наличии продольно-поперечного расщепления и фиксированного расщепления по поляризациям в x- и y-направлениях, существующего из-за оптической анизотропии материала микрополости. В этом случае в дисперсии поляритонов, расщепленной по поляризациям, образуются две точки вырождения, показанные на рисунке. В их окрестности на поляритоны действует суммарное псевдомагнитное поле, уже имеющее вид калибровочного.

А поскольку это поле действует на спинорную волновую функцию поляритонов как матрица, оно оказывается еще и неабелевым.

#поляритоны #фотоника

Принято считать, что электрический ток в металлах переносится электронами, но это не всегда верно. Типично «электронные» – лишь щелочные металлы, а в большинстве других сосуществуют электроны и дырки из различных карманов поверхности Ферми. Сами поверхности Ферми могут быть настолько искривленными и запутанными, что даже сложно сказать, чем именно являются квазичастицы вблизи каждой их точки – электронами, дырками или еще какими неведомыми зверьми.

Казалось бы, преимущественно электронный или дырочный характер металла можно определить по знаку эффекта Холла, который зависит от знака заряда носителей тока. Но здесь тоже не все так просто: оказывается, холловская проводимость может иметь разные знаки, не связанные напрямую с видом квазичастиц. При этом она допускает интересную геометрическую интерпретацию как поток, проходящий через некоторый контур. Об этом – в следующей небольшой статье.

https://telegra.ph/Poverhnosti-Fermi-v-metallah-i-geometricheskaya-interpretaciya-hollovskoj-provodimosti-07-20

#твердое_тело

Эксперимент с красивым наблюдением эффекта Джозефсона в атомном газе. Это газ атомов-фермионов ⁶Li, который при слабом притяжении становится сверхпроводником с конденсатом куперовских пар, а при сильном притяжении – бозе-конденсатом молекул-бозонов.

Сигарообразное атомное облако разделяется на две части туннельным барьером, созданным дополнительным лазерным лучом. Для запуска джозефсоновских осцилляций потенциал ловушки вместе с барьером резко смещаются вбок, так что в облаке создается дисбаланс химических потенциалов слева и справа (A). Сами осцилляции можно наблюдать, измеряя как населенности двух конденсатов в половинках атомного облака (B), так и разность их фаз по интерференционной картине, возникающей после выключения барьера (C).

Джозефсоновские осцилляции наблюдаются на всем протяжении кроссовера БКШ-БЭК. К примеру, графики снизу показывают осцилляции дисбаланса населенностей Z и разности фаз φ в режиме бозе-конденсации (слева) и в унитарном режиме (справа).

#атомные_газы #сверхпроводимость

Киральные метаповерхности позволяют поддерживать поверхностные плазмоны, распространяющиеся в разные стороны при противоположных циркулярных поляризациях.

Вот пример такой поверхности: это металлическая пленка, в которой вырезаны прямоугольные отверстия с меняющимися направлениями. Киральные плазмоны такой метаповерхности связываются с экситонами близлежащего слоя WS₂ в поляритоны. Из-за их киральности, авторы предлагают называть их киралитонами.

На диаграммах снизу демонстрируется, что эти поляритоны действительно киральны: при противоположных циркулярных поляризациях антипересечения плазмонной и экситонной дисперсий происходят на противоположных волновых векторах k_x. Это видно как на спектрах отражения (диаграммы сверху), так и на спектрах генерации второй гармоники (диаграмма снизу), попадающей в энергию верхнего поляритона. А из-за особенностей WS₂ получается, что в разных направлениях движутся поляритоны, содержащие экситоны из противоположных долин.

#фотоника #плазмоны #поляритоны

Инерциальный термоядерный синтез состоит в том, что материал, содержащий дейтерий или тритий, ионизуется мощными лазерами. Из-за резкого нагрева ядра разгоняются до энергий, позволяющих им преодолевать кулоновский барьер.

Но такие затеи требуют мощных лазерных установок, а в этой работе удалось достичь ядерного синтеза с использованием обычного, «настольного» фемтосекундного лазера с энергией импульса 120 мДж. Как показано на схеме, струя дейтерия распыляется в вакуум, образуя кластеры размером 50 Å. Лазерный импульс ионизует их, превращая поток кластеров в плазменную струю – она видна на интерференционной картине пропущенного через нее света.

Средняя энергия ядер дейтерия в плазме составляет 2.5 кэВ – этого хватает для преодоления кулоновского барьера с достаточно большой вероятностью, так что каждый импульс создает порядка 15000 нейтронов, испускаемых после слияния в ядро ³He. Энергия таких нейтронов должна быть равна 2.45 МэВ, и это подтверждается измеренным спектром, показанным внизу.

#ядерная_физика

Любопытные формулы для сверхтекучей плотности, которую авторы этой статьи называют «друдевским весом» D_w.

Как показано сверху, она выражается через среднюю кинетическую энергию и сумму, содержащую матричные элементы оператора тока J между основным |Ψ_0> и точными многочастичными возбужденными состояниями |Ψ_m>. Эта сумма похожа – с точностью до другой степени знаменателя – на выражение для многочастичной квантовой метрики g(0) на оси проходящего через систему магнитного потока. Если все энергии возбуждений E_m – E_0 не меньше щели ε, мы получаем неравенство, показанное снизу.

Первое слагаемое обычно отрицательно, так что g уменьшает сверхтекучую плотность по сравнению с ее максимально возможным значением. Интерпретация этого факта такова: чем выше многочастичная квантовая метрика g, тем сильнее многочастичная волновая функция системы искажается при внесении возмущения, создающего сверхтекучий ток. Это не дает системе просто ускоряться как целое, уменьшая сверхтекучий отклик.

#сверхтекучесть

Недавно я писал о том, как добавление солей нарушает скоррелированность дипольных моментов молекул воды и, тем самым, понижает ее диэлектрическую проницаемость ε. А в этой работе показано, почему у чистой воды высокая ε: действительно, она обусловлена тем, что из-за направленности водородных связей дипольные моменты соседних молекул воды направлены почти в одну сторону.

Простейшая теория линейного отклика дает формулу ε = 1 + (4π/3)<M²>/VT, где M – суммарный электрический дипольный момент всех молекул в объеме V. При этом <M²> = Nμ²G, где μ –дипольный момент каждой молекулы, G – мера их скоррелированности по направлениям, которую можно посчитать как интеграл от парной корреляционной функции c_m(r) ~ <μ(0)•μ(r)>. На графике видно, что c_m(r) имеет пик на расстоянии между ближайшими соседями – там же, где похожий пик демонстрирует корреляционная функция для атомов кислорода g_OO.

Из-за значительной сонаправленности соседних диполей G достигает 2.2 – это и есть вклад корреляций в увеличение ε.

#химия

Квантовый выход фотолюминесценции – это число фотонов, испускаемых в расчете на одну электрон-дырочную пару, образующуюся при накачке. У двумерного полупроводника MoS₂ он обычно составляет 1%. А здесь, после обработки образцов суперкислотой, его удалось повысить практически до 100%!

Сверху видно, как отличается люминесценция в только что изготовленном (синяя кривая) и в обработанном (красная кривая) образцах – по интенсивности она увеличивается в 190 раз, хотя форма спектральной линии сохраняется. Внизу показано, как квантовый выход и время жизни носителей (измеренное по сверхбыстрой люминесценции) зависят от интенсивности накачки. После обработки обе величины увеличиваются на два порядка. Но при сильной накачке они постепенно снижаются из-за образования и рекомбинации биэкситонов при высокой концентрации электрон-дырочных пар.

Авторы предполагают, что обработка суперкислотой подавляет процессы нерадиативной рекомбинации, удаляя с образца примеси и пассивируя дефекты.

#дихалькогениды_переходных_металлов