Стоит отметить, что рассмотренный выше фазовый переход является так называемым среднеполевым фазовым переходом 1-го рода. Он возникает в системе с дальними взаимодействиями, в которой не образуется пространственного разделения фаз – для нее вообще бессмысленно говорить о пространстве, поскольку все спины одинаково взаимодействуют со всеми.

Вообще, фазовые переходы 1-го рода возникают из-за невыпуклости термодинамического потенциала (b), приводящей к участку нестабильности на фазовой диаграмме (a). Но нестабильность актуальна только в случае пространственно однородной системы (для которой этот график и нарисован), потому разрешается расслоением системы на две фазы. Невыпуклость термодинамического потенциала также при этом сглаживается.

Но бывает и среднеполевой фазовый переход 1-го рода, когда в системе есть дальние взаимодействия, и на фазы расслоиться она не может. В этом случае термодинамический потенциал остается невыпуклым, и нарушается эквивалентность ансамблей.

#фазовые_переходы #объяснения

Симметрия по отношению к обращению времени (T-симметрия) нарушается в твердых телах внешним магнитным полем или магнитным упорядочением. Ее легко нарушить и при создании аналогов твердых тел на основе электрических цепей или ультрахолодных атомов в оптических решетках. Но что с механическими метаматериалами?

В этой работе был создан аналог модели Холдейна в виде механического метаматериала, состоящего из гироскопов. Здесь небольшие электродвигатели подвешены в виде решетки «пчелиные соты». Вращение небольших цилиндров нарушает T-симметрию, а отталкивание прикрепленных к ним вертикальных магнитов создает взаимодействие между соседними гироскопами. Такая система является топологически нетривиальной и поддерживает краевые моды, распространяющиеся по границе только в одном направлении. Это и показано на видео: раскачка одного из гироскопов с частотой, лежащей в щели спектра возбуждений толщи запускает однонаправленную волну, не заходящую в толщу и огибающую неровности.

#топологические_материалы #механика

Возмущения в протяженной квантовой системе с локальными взаимодействиями распространяются с определенной скоростью, называемой butterfly velocity – скоростью распространения «эффекта бабочки». В этой работе показано, что динамика распространения возмущения по квантовой системе зависит от того, отвечает ли оно сохраняющейся величине. Здесь можно провести аналогию с гидродинамикой: при локальном сохранении числа частиц и их суммарного импульса можно говорить о макроскопических потоках жидкости, характеризующихся как раз этими сохраняющимися величинами – плотностью и скоростью. Поэтому теорию квантовых систем с локально сохраняющимися операторами называют обобщенной гидродинамикой.

Динамику оператора, отвечающего локально сохраняющейся величине (например, проекции S_z в цепочке спинов, где S_z может лишь распространяться по системе, но не меняться глобально), можно описать при помощи плотности этого оператора, то есть перекрытия его гейзенберговски проэволюционировавшей версии с исходным оператором на конкретном узле (например, S_zᵢ). Важно, что не вся плотность оператора отвечает его локально сохраняющейся части: например, гейзенберговски проэволюционировавший оператор S_z₀ может содержать слагаемые, отвечающие не только локальным переворотам спина S_zᵢ на каком-то одном i-м узле, но и несколько переворотов спинов в разных местах, а это уже несохраняющаяся часть.

Вот что происходит с плотностью оператора локально сохраняющейся величины:
• Сохраняющаяся часть плотности оператора претерпевает медленную диффузию из начальной точки, демонстрируя скопление вблизи нее, ширина которого растет по обычному диффузионному закону (Dt)¹ᐟ².
• Часть плотности оператора при этом конвертируется в несохраняющуюся компоненту, которая с самого начала распространяется по системе баллистически, со скоростью «эффекта бабочки», и образует два резко очерченных волновых фронта, идущих налево и направо (в одномерной системе).
• Центральное диффузионное пятно при этом продолжает в каждый момент времени генерировать все новые несохраняющиеся компоненты, которые идут вдогонку изначальным волновым фронтам с той же скоростью, образуя за ними степенные хвосты.

Это можно сравнить с распространением тепла в системе частиц: резкое поступление энергии в какую-то ее точку создает одновременно ударную волну, распространяющуюся баллистически со скоростью звука, и идущую следом более медленную диффузию тепла. Интересно, что скорость генерации несохраняющихся компонент – то есть диссипации локально сохраняющейся величины – пропорциональна скорости потока последней, что аналогично обычной, механической диссипации. Еще один любопытный момент в том, что несохраняющиеся компоненты оператора быстро хаотизуются, становясь сильно нелокальными и приобретая высокую энтропию – это значит, что в дальнейшем их становится практически невозможно детектировать или модифицировать при помощи локальных измерений. Здесь тоже аналогия с распространением энергии: превращаясь в тепло, она рассеивается по большому числу степеней свободы, так что ее трудно после этого сконцентрировать обратно.

#квантовая_механика

Сверху на рисунке показано, как, в разные моменты времени, выглядит плотность оператора локально сохраняющейся величины, которая распространяется из начальной точки влево (пунктирные линии), либо вправо (сплошные линии).

Можно видеть постепенно расширяющееся диффузионное скопление в центре, два баллистических волновых фронта (которые, впрочем, тоже постепенно расплываются из-за диффузии) и степенные хвосты за этими фронтами.

Совсем иначе выглядит картина распространения оператора локально несохраняющейся величины, показанная снизу. Здесь диффузионное пятно отсутствует, а имеются лишь два волновых фронта. Это типичная картина распространения «эффекта бабочки» по системе, ограниченного квантовым пределом скорости.

#квантовая_механика #гидродинамика

Правила Юм-Розери (Hume-Rothery rules) помогают понять, будут ли два конкретных металла образовывать твердый раствор – сплав, в котором атомы одного элемента в случайных узлах решетки заменяются атомами другого элемента.

Эти правила следующие:
1) Радиусы атомов должны отличаться не более чем на 15% – в противном случае выстраивание разных атомов в единую решетку будет вызывать слишком сильные напряжения.
2) Кристаллические структуры обоих смешиваемых металлов должны быть похожими. Не обязательно одинаковыми – например, гранецентрированная кубическая и гексагональная плотноупакованная тоже подойдут в виду своего сходства.
3) Валентности элементов должны быть близкими – хотя подмешиваемый элемент может иметь и более высокую валентность.
4) Степени электроотрицательности элементов тоже должны быть близкими: чем они ближе, тем выше растворимость одного металла в другом. При слишком большом различии металлы образуют интерметаллическое соединение – по сути, стохиометрическое химическое соединение.

#твердое_тело

Базовые модели (foundation models) – это недавно появившийся термин, используемый для мощных нейронных сетей, которые обучаются на огромных, разнообразных массивах данных и затем доучиваются для выполнения различных частных задач. К примеру, большая языковая модель, предобученная моделировать язык – то есть угадывать следующее слово в незаконченном тексте – затем может доучиваться для выполнения задач юридических консультаций или проверки школьных домашних заданий по химии. Многие полагают, что появление базовых моделей знаменует глобальный сдвиг парадигмы в практике машинного обучения, да и вообще в сфере работы с информацией.

Считается, что базовая модель, в ходе своего обучения, улавливает важнейшие закономерности тех данных, с которыми она будет работать – например, грамматическую структуру естественного языка и семантику наиболее часто встречающихся слов. Это позволяет ей выполнять широкий спектр задач с этими данными, иногда после дополнительного дообучения. Здесь проявляется важное свойство базовых моделей – эмерджентность, то есть проявление способностей, которые при обучении не закладывались в модель в явном виде. Например, большая языковая модель, обученная моделированию языка, оказывается способной решать несложные математические задачи.

Также базовые модели зачастую демонстрируют перенос обучения, или трансферное обучение: обучение модели для выполнения одной задачи позволяет ей выполнять другие задачи или, по крайней мере, улучшает степень их выполнения. К примеру, модель, обученная распознаванию образов на статичных картинках, потом распознает действия людей на видео. Базовые модели можно условно разделить на работающие с текстами (большие языковые модели) и работающие с пространственные данными (изображения, видео, движение роботов в пространстве). Хотя сейчас популярны и мультимодальные модели, но они часто состоят из нескольких моделей разных типов, специальным образом соединяемых.

Стоит отметить и важные особенности обучения базовых моделей. Во-первых, они обучаются на гигантских и автоматизированно собираемых массивах данных. Во-вторых, они обучаются методом, который называется self-supervised learning – «самообучением». Он основан на массивах данных, которые явным образом не размечены, но их можно эффективно разметить в автоматизированном режиме. К примеру, скрывая в тексте произвольные слова, можно добиваться того, чтобы большая языковая модель их угадывала – и, в процессе обучения, награждать ее за верные угадывания и штрафовать за ошибочные.

В этом обзоре, написанным большим коллективом авторов, описываются современные области применений базовых моделей, связанные с ними проблемы и потенциальные риски, а также перспективы будущего развития.

#нейронные_сети #популярное

🥊 Машинная модель, предназначенная управлять роботом, может попытаться ударить или нокаутировать работающего с ней оператора-человека, если ее обучающие данные включали видео боксерских матчей.

#цитаты

Отдельный интересный вопрос, обсуждаемый в обзоре по базовым моделям: понимают ли нейронные сети смысл данных, с которыми они работают?

Здесь сразу стоит отметить, в чем специфика таких моделей, и почему ответ на этот вопрос в принципе может быть отрицательным. Большая языковая модель зачастую обучается методом self-supervised learning, когда ей предъявляют тексты со случайным пропущенным словом, и от нее требуется это слово правильно угадать. Таким образом, информацию о значении слова модель получает лишь косвенным образом, через контекст – по тому, какие другие слова (и на каких позициях) встречаются рядом с этим словом. А значения этих самых других слов тоже определяются косвенно, через контекст. В отличие от человека, языковая модель не получает представления о смысле слова через непосредственный опыт – визуальный, слуховой, тактильный, моторный (то есть опыт физических манипуляций с предметами). Хотя бывают и мультимодальные модели, обучающиеся совместно на визуальных и текстовых данных, но это пока редкость.

Понимают ли машинные модели смысл слов естественных языков – не совсем праздный вопрос, поскольку от ответа на него зависит, насколько мы можем доверять результатам их работы и насколько интерпретируем их процесс генерации – то есть насколько мы сами понимаем, как они работают и чем мотивированы те или иные результаты генерации. В философии существуют три основных взгляда на то, что значит «понимать язык»:
• Интернализм: понимание языка означает построение его правильного внутреннего представления в ответ на поступающую на вход текстовую информацию.
• Референциализм: субъект понимает язык, если он может оценить, являются ли конкретные предложения на нем истинными – относительно предъявленного конкретного контекста, ситуации, сценария.
• Прагматизм: субъект понимает язык, если может правильно его использовать на практике – то есть, генерировать новые предложения и использовать разговорные приемы, отвечающие принятым в языке правилам.

Для многих достаточно мощных языковых моделей уже можно сказать, что они понимают язык с точки зрения прагматизма. Но проблема в том, что факт такого понимания ничего не говорит о том, можем ли мы доверять правильности суждений модели или сами понимать логику их получения. В свою очередь, интернализм и референциализм сводятся к проблеме отображения: может ли модель неким правильным образом отображать тексты на математически-логические объекты (внутренние представления) либо на значения истина/ложь. Достаточно ли для этого обучения лишь на текстовых примерах, без дополнительного опыта в других модальностях – большой вопрос.

Можно представить себе попавшего на Землю пришельца из другой вселенной с другими законами, который изучил наш язык по огромной базе текстов и выдает себя за человека. Можем ли мы поставить его в такую ситуацию, где его знаний языка окажется недостаточно для правильной, человеческой реакции? Если сложность получаемого нами опыта столь велика, что никакой объем текстовой информации полностью его не покроет, то такие ситуации должны существовать.

#нейронные_сети #популярное

А еще авторы обзора отдельно сетуют на то, что ученые-исследователи постепенно теряют доступ к самым мощным базовым моделям. В свое время, сообщество специалистов по машинному обучению установили высокие стандарты открытости и стандартизации программного кода и публично доступных баз, которые потом проникли и в другие дисциплины.

Но с появлением базовых моделей этот позитивный тренд развернулся. Многие модели (начиная с GPT-3) и обучающие выборки для них вообще не выкладываются в открытый доступ. Коммерческие компании, такие как OpenAI и Google, имеют несравнимо больше финансовых и вычислительных ресурсов, а также возможностей доступа к огромным массивам обучающих данных, чем академические исследователи, поэтому могут обучать гораздо более мощные модели – и этот отрыв с годами только растет.

Возможный способ преодолеть этот разрыв – это крупный межгосударственный проект, наподобие телескопа «Хаббл» и Большого адронного коллайдера, но теперь в сфере искусственного интеллекта.

#нейронные_сети #популярное

Спросил у ИИ, кто ведет мой телеграм-канал - ответ на картинке.

Вообще, сейчас многие начали использовать чат-боты для фактчекинга, думая, что это некие справочные центры, в которые «заложены» большие массивы проверенных данных. Хотя в действительности это генераторы текстов, работающие по не совсем понятным нам принципам, вдобавок со значительным элементом случайности.

#цитаты

Когерентное идеальное поглощение – это обращенный во времени аналог лазера (антилазер), при котором две волны, поступающие в систему с разных сторон, полностью поглощаются без выходящих волн. В этой работе придуман и экспериментально реализован тепловой аналог когерентного идеального поглощения.

Авторы заметили, что уравнения распространения тепла в радиальном направлении похожи на задачу о рассеянии электромагнитной волны с чисто мнимым волновым вектором, если рассматривать угловую гармонику T ~ cos θ. На рисунке показаны ситуации, где в среду помещен полый цилиндр с большей (слева) или меньшей (справа) теплопроводностью. Температурные профили, ведущие себя как T ~ r или как T ~ 1/r, аналогичны волнам, падающим на цилиндр снаружи или изнутри. Как видно на разрезах снизу, в обоих случаях имеется «полное поглощение»: и снаружи, и изнутри имеются только падающие волны. Иными словами, цилиндр «невидим» для внешнего теплового потока и не нарушает однородность его температурного градиента.

#твердое_тело

🤯 Существуют сходства между распространением слухов и взрывом атомной бомбы – оба этих процесса имеют характер перколяции в мультифрактальной сети цепных реакций.

#цитаты

Недавний эксперимент, где изготовили наномеханические резонаторы с рекордной добротностью в виде натянутых алмазных нитей. Слева показан принцип их изготовления: тонкие алмазные нити, полученные химическим и плазменным травлением, подвешивались близко сведенными параллельными парами. Далее на них конденсировалась капля жидкости, сводящая две нити вместе за счет поверхностного натяжения. После испарения капли нити оставались соединенными благодаря их собственному ван-дер-ваальсовскому прилипанию.

Соединение двух нитей посредине натягивает их до напряжений 1.3 Гпа, чего сложно достичь другими методами изготовления. Сильно натянутые нити вибрируют подобно струне, причем с высокой добротностью благодаря эффекту разбавления диссипации (tension-induced dissipation dilution). На диаграмме показана добротность полученных устройств в сравнении с конкурентами – при криогенных температурах здесь достигаются величины 10¹², являющиеся рекордом для любых механических резонаторов вообще.

#механика #наноструктуры

Изготовленные в этом эксперименте алмазные нанорезонаторы настолько чувствительны, что позволяют детально исследовать источники своей диссипации и сдвига своих частот.

К примеру, по температурной зависимости скорости диссипации было обнаружено, что главный ее источник – это дефекты на поверхности алмаза, в частности, квантовые роторы в виде OH-групп. Детальные же измерения при температурах ниже 3 К показывают, что заметная часть диссипации происходит благодаря диссоциировавшим парам квантованных вихрей в пленке жидкого гелия, окружающего и охлаждающего нанорезонаторы. А показанный на графике сдвиг резонансной частоты при температурах ниже сверхтекучего перехода обусловлен, предположительно, акустическим эффектом Казимира в пленке жидкого гелия.

#наноструктуры #сверхтекучесть

В этой работе развивается телепараллельная теория дефектов в твердых телах. Она основана на телепараллельной геометрии, в которой пространство не имеет кривизны, но имеет кручение. Благодаря этому, относительные ориентации тройки базисных векторов в двух отдаленных точках пространства всегда можно соотнести между собой, проверив, параллельны ли они или повернуты друг относительно дружки – отсюда и телепараллельность (то есть параллельность на расстоянии).

#твердое_тело #математика

Газ киральных электронов в однослойном и двухслойном графене не обладает инвариантностью по отношению к преобразованиям Галилея. Причина не только в линейной дисперсии (как в однослойном графене), но и в существовании псевдоспина, связанного с двумя подрешетками. Как показано слева на рисунке (на примере однослойного графена), при сдвиге сферы Ферми, отвечающем разгону электронного газа как целого, псевдоспиновая текстура не сдвигается вместе с ней, так что разгон электронного газа не компенсируется переходом в другую систему отсчета.

Одно из следствий галилеевой неинвариантности – это многочастичная перенормировка друдевского веса, от которого зависит групповая скорость плазмонов. В этом эксперименте последняя была определена методом SNOM по наклону плазмонных мировых линий (рисунок справа). Графики снизу показывают измеренный друдевский вес как функцию уровня допирования, который отклоняется от «наивной» теории, не учитывающей его перенормировку (пунктирные кривые).

#графен #плазмоны

При квантовой телепортации энергии Алиса производит над системой измерение (тем самым вкладывая в нее энергию) и пересылает результат измерения Бобу. Эта информация служит «ключом», благодаря которому Боб может сразу извлечь из системы энергию, не дожидаясь, когда она дойдет до него естественным путем, со скоростью Либа-Робинсона.

В этой работе рассмотрена времяподобная квантовая телепортация энергии, при которой Боб ждет, когда до него доберется созданное Алисой возмущение системы, и только после этого производит над системой операцию, зависящую от информации, также полученной от Алисы. Оказывается, так можно передать от Алисы к Бобу значительно большую долю энергии, чем обычной квантовой телепортацией – например, 40% против 3% для случая цепочки Изинга. В качестве примера, на рисунке показан объем дополнительной энергии, которую Боб может извлечь с использованием информации от Алисы, как функция времени. Как видно, для этого есть как наиболее выгодный, так и невыгодные моменты.

#квантовая_механика

При обсуждении второго начала термодинамики, тепловой смерти Вселенной и причины стрелы времени еще в XIX веке был поставлен вопрос: а не может быть такое, что тепловая смерть Вселенной уже давно произошла, а мы наблюдаем вокруг себя лишь временное отклонение от нее в результате случайной флуктуации?

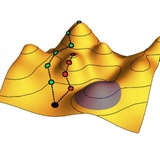
На рисунке показано типичное поведение энтропии изолированной системы с течением времени. В норме энтропия остается на своем максимальном значении – это состояние тепловой смерти. Но из-за случайных флуктуаций система может от него отступать – тогда энтропия временно уменьшается, а затем снова растет. Чем крупнее такие отступления, тем реже они встречаются, но теорема Пуанкаре о возвращении гарантирует, что за бесконечно большое время можно дождаться сколь угодно сильных отклонений энтропии от максимального значения.

Так что возникает резонный вопрос: не живем ли мы все во время одной из таких флуктуаций?

#термодинамика #популярное

На этот аргумент сразу же возникло следующее возражение. Чем крупнее флуктуация по своему масштабу, тем с меньшей вероятностью она произойдет. При этом зависимость вероятности от масштаба флуктуации экспоненциальная: каждый кубометр объема флуктуации уменьшает ее вероятность на много-много порядков, так что наиболее вероятными должны быть самые скромные флуктуации.

Представим теперь, что наблюдаемая нами Вселенная – сильно отклоняющаяся от равновесия из-за наличия плотных горячих звезд в холодном темном пространстве – возникла в результате флуктуации на фоне тепловой смерти, где все равномерно теплое и серое. Она избыточно велика: ведь для появления людей, которые могли бы удивиться неравновесности окружающего их мира и задаться вопросом о происхождении стрелы времени и причинах второго начала термодинамики, было бы достаточно одной лишь Солнечной системы.

Поэтому появление в результате флуктуации «маленькой Вселенной», где есть только Солнечная система, окруженная хаосом тепловой смерти, неимоверно более вероятно, чем та огромная Вселенная с миллиардами галактик, которую мы наблюдаем. Следовательно, и для любого разумного существа вероятность оказаться в большой Вселенной-флуктуации практически равна нулю по сравнению с вероятностью обнаружить себя в маленькой Вселенной. Таким образом, появление наблюдаемой Вселенной в результате случайной флуктуации не имеет разумного объяснения.

Можно пойти дальше, задавшись вопросом: а кто сказал, что эта самая «большая Вселенная» с миллиардами галактик действительно существует? Может быть, в результате флуктуации образовался лишь один-единственный мозг, окруженный тепловым хаосом и живущий в иллюзиях? Появление такой минимальной по масштабу системы куда более вероятно, чем даже Солнечной системы, не говоря уже о наблюдаемой нами Вселенной. Так и появилась концепция больмановского мозга: некой осознающей себя сущности, возникшей случайно из-за флуктуации и убежденной, что она живет в большой Вселенной – но на самом деле одинокой и скоротечной.

#термодинамика #популярное #объяснения

Хотя гипотеза больцмановского мозга выглядит нонсенсом, ее сложно опровергнуть. Наше появление в результате относительно небольшой флуктуации действительно куда более вероятно, чем в результате масштабной флуктуации, начавшейся с Большого взрыва. Можно поставить вопрос иначе, отойдя от обсуждения висящего в пустоте одинокого мозга: насколько вероятно то, что наша Вселенная действительно началась с Большого взрыва – то есть очень маловероятного и сильно отклоняющегося от равновесия состояния, – а не возникла секунду назад из-за случайной флуктуации в текущем состоянии, с готовыми свидетельствами прошлого и готовыми воспоминаниями в наших мозгах?

Второй вариант не только более вероятен, но и согласуется со вторым началом термодинамики. Действительно, второе начало термодинамики гласит, что энтропия изолированной системы (например, всей нашей Вселенной) должна с гораздо большей вероятностью расти с течением времени, чем убывать. И этот вывод не зависит от направления времени: энтропия с большой вероятностью должна расти как в будущее, так и в прошлое. Иными словами, если взглянуть на картинку выше с клинообразными провалами на зависимости энтропии Вселенной от времени, то всегда наиболее вероятно то, что мы находимся в точке C в самом низу провала (когда энтропия минимальна в настоящий момент и растет со временем в обе стороны), чем в точке A на его склоне, когда энтропия в прошлом была еще ниже, чем сейчас.

Брайан Грин в книге «Ткань космоса» приводит такой пример: представим себе яйцо, падающее со стола на пол и разбивающееся, тем самым перехода из более упорядоченного состояния в менее упорядоченное. Это можно считать процессом, в котором энтропия необратимо растет с течением времени, что согласуется с нашим опытом. Но что было в прошлом, до падения яйца со стола? Если мы запустим время с этого момента в сторону прошлого, то энтропия тоже должна расти: яйцо точно так же, с большой вероятностью, упадет со стола и разобьется. Запустив время в нормальную сторону, мы увидим парадоксальную ситуацию: разбитое яйцо само собой собирается с пола и запрыгивает на стол, после чего падает обратно на пол и разбивается.

Вторая половина этого процесса кажется нам нормальной, первая же – абсурдной. Ведь очевидно, что яйцо появилось на столе не самопроизвольной сборкой из лужи на полу, а его снесла курица. Но это лишь на первый взгляд, пока мы не начали оценивать вероятности. Да, спонтанная сборка яйца и запрыгивание его на стол из-за случайной флуктуации движения молекул выглядит очень маловероятной (хотя и не невозможной в принципе). Но ведь существование в прошлом курицы – гораздо более сложного и упорядоченного объекта, чем яйцо – еще менее вероятно! Аналогично, появление нашей Вселенной секунду назад в готовом виде в результате флуктуации тоже куда более вероятно, чем возникновение в отдаленном прошлом Большого взрыва.

Таким образом, гипотеза больцмановского мозга – если называть таковой наше существование в настоящий момент на самом дне случайного провала энтропии – действительно представляется весьма вероятной, если абстрагироваться от обыденного здравого смысла и рассуждать более формально. Хотя в недавней работе было замечено, что ее обоснование содержит логическую ошибку: мы выводим ее из комбинации известных нам законов природы (например, второго начала термодинамики) и наблюдаемых данных о текущем состоянии Вселенной (неравновесное и низкоэнтропийное состояние). Но законы природы сами ведь являются следствием наблюдаемых данных, а вовсе не независимым от них положением. Если учесть эту зависимость и правильно применить теорему Байеса, то вероятность справедливости гипотезы больцмановского мозга из близкой к 1 становится близкой к 0, что уже согласуется с нашим здравым смыслом.

#термодинамика #популярное