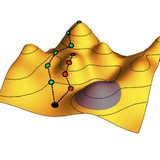
Хорошая иллюстрация из статьи по топологической фотонике, о которой я недавно писал. Она показывает, чем аналитическая функция, удовлетворяющая условиям Коши-Римана, отличается от неаналитической.

Слева показана фаза комплексной функции, полученной в результате суперпозиции 8 плоских волн со случайными амплитудами и различными волновыми векторами. Стрелочки показывают получившиеся вихри и антивихри – точки, при обходе вокруг которых фаза набегает на 2π или –2π.

Справа же показана аналитическая функция переменной z = x + iy. У нее на плоскости нет полюсов и существенно особых точек, а могут быть лишь нули. Вокруг каждого нуля z₀ функция ведет себя как z – z₀, а значит, получает набег фазы 2π при обходе против часовой стрелки.

В итоге, аналитическая функция получается в целом «закрученной» против часовой стрелки, в то время как случайная функция такой преимущественной закрученности не демонстрирует.

#объяснения

Диэлектрическая проницаемость воды ε, как показано на графике, заметно уменьшается при растворении в ней поваренной соли. С 1926-го года это объясняли диэлектрическим насыщением: молекулы воды выстраиваются вокруг ионов в гидратационные оболочки и направляются своими дипольными моментами либо к иону, либо от него (в зависимости от его заряда). Это затрудняет повороты дипольных моментов молекул воды под действием внешних полей, уменьшая ε.

В этой работе при помощи молекулярно-динамических расчетов с нейросетевыми потенциалами модель диэлектрического насыщения была опровергнута. Оказывается, причина уменьшения ε в том, что вмешательство ионов нарушает сетку водородных связей. В чистой воде благодаря этой сетке ближайшие диполи почти сонаправлены и поэтому могут откликаться на внешнее поле коллективно – сильнее, чем по отдельности. В соленой же воде они вблизи ионов могут быть почти антипараллельны (как показано синими стрелками), из-за чего коллективный отклик молекул воды подавляется.

#популярное #химия

Заполнение электронами одночастичных состояний в порядке возрастания их энергий называют принципом Ауфбау. В этой работе показывается, что такой же принцип справедлив и для неэрмитовых систем с комплексными энергиями, только одночастичные заполняются в порядке возрастания вещественных частей их энергий.

Еще один интересный момент показан на рисунке. В одномерной модели Хатано-Нельсона (с несимметричными перескоками вправо и влево) с открытыми граничными условиями частицы скапливаются возле левого края. Диаграммы показывают импульсное (слева) и координатное (справа) распределения в нескольких низших по энергии многочастичных состояниях l для системы 5 фермионов (сверху) или бозонов (снизу).

Видно, что фермионы образуют нечто вроде сферы Ферми (b) и скапливаются вблизи края, насколько позволяет принцип Паули ((a), l=1 для основного состояния). Бозоны же конденсируются как в импульсном пространстве (d), так и в координатном ((c), l=1). Этот факт авторы называют «аномальной конденсацией».

#неэрмитовы_системы

Полюсы и нули функций отклика электромагнитной системы на комплексной плоскости частот ω дают информацию, соответственно, о ее собственных модах и о точках полного поглощения.

Авторы этой статьи обращают внимание на метод численного нахождения полюсов и нулей, основанный на контурном интегрировании по комплексной плоскости. К примеру, мы рассматриваем метаповерхность в виде массива диэлектрических усеченных конусов и, численным решением уравнений Максвелла, находим ее функцию отклика, – например, коэффициент отражения q(ω), – вдоль контура комплексных частот, показанного черными точками. Посчитав интегралы от ωⁿq(ω) с разными степенями n, по ним можно найти положения нулей и полюсов внутри контура – они показаны красными и синими точками. Таким образом, не требуется решать уравнения Максвелла на всей плоскости комплексных частот.

Правда, не стоит забывать, что такой метод применим лишь в том случае, когда оптические константы материалов хорошо определены на комплексных частотах.

#фотоника

Циркулярно поляризованная электромагнитная волна заставляет электроны в облучаемом материале двигаться по кругу. В этом эксперименте показано, что это может создавать магнитное поле до 0.7 Тл, если облучать графеновые нанодиски терагерцовыми импульсами.

Импульс частотой 3.5 ТГц попадает в резонанс с дипольным плазмоном на графеновых дисках диаметром 1.2 мкм. При их облучении циркулярно поляризованным импульсом образуется суперпозиция двух перпендикулярных дипольных плазмонов, сдвинутых по фазе на π/2, то есть циркулярный плазмон с круговым током. Снизу показан результат моделирования магнитного поля, создаваемого таким током.

Его можно обнаружить по аналогу эффекта Фарадея, то есть по вращению плоскости поляризации второго, зондирующего терагерцового импульса, имеющего изначально линейную поляризацию. Даже при не очень большой интенсивности накачки угол вращения достигает 1°, что сравнимо с результатом обычного эффекта Фарадея во внешнем магнитном поле 0.7 Тл.

#плазмоны #графен

Связанные состояния в континууме – сейчас популярная тема, особенно в применении к фотонным кристаллам. Обычно это сугубо одночастичные состояния – решения уравнений Шредингера или Максвелла для одной волны. А в этой работе было численно доказано существование многочастичных связанных состояний в континууме.

Авторы взяли одномерную модель Бозе-Хаббарда с примесью – бозоны, которые перескакивают по цепочке, притягиваются друг к другу, оказавшись на одном узле, а также притягиваются к примеси в центре. На диаграмме показан численно найденный спектр энергий многочастичных состояний E как функция силы межчастичного притяжения U, а цвет дает представление о протяженности волновой функции.

Можно видеть как дискретные связанные (синие), так и континуумы протяженных (зеленых) состояний. А стрелочками указаны связанные состояния, попадающие прямо в полосы континуума. На вставке их можно видеть более четко. Это случай системы 4 частиц, но авторы нашли подобные состояния и в 6-частичной системе.

#квантовая_механика

Занятный расчет сил притяжения между двумя сверхпроводниками, основанный на теории Гинзбурга-Ландау. Авторы рассматривают сверхпроводник, взаимодействующий с электромагнитным полем, и для них выводят эффективный гамильтониан, содержащий энергию поля и сверхпроводящего тока, а также «упругую» энергию, связанную с градиентами электронной плотности.

Взяв два ступенчатых профиля плотности положительно заряженных ионов (черный пунктир), авторы посчитали распределение электронной плотности, минимизирующее полную энергию (сплошная оранжевая линия). Это ситуация двух сверхпроводящих пластин, разнесенных на расстояние L. На графиках справа показаны полная энергия и действующая между пластинами сила как функции L: видно, что между ними существует притяжение, максимальное на расстояниях порядка длины залечивания плотности ξ.

Не знаю, насколько корректен этот расчет с точки зрения теории эффекта Казимира (там много всяких тонкостей), но результат здесь, по крайней мере, получается сходящимся.

#сверхпроводимость

А вот еще интересные соотношения из статьи из предыдущего поста: рассматривая малые возмущения скорости движения электронов сверхпроводника в виде плоской волны, авторы получают их дисперсии, показанные на картинке. Они различаются, в зависимости от поляризации волны.

Продольные колебания – это возмущения плотности. В статическом пределе они спадают в пространстве на масштабах длины залечивания ξ, связанной с лондоновской глубиной проникновения λ_L и длиной когерентности λ_C. В динамике же их дисперсия выходит из плазменной частоты ω_p при k = 0 и становится квадратичной в коротковолновом пределе k → ∞.

В то же время, поперечно поляризованные колебания – это электромагнитные волны, экранированные сверхпроводником. В статике они спадают на расстоянии λ_L – это обычное лондоновское экранирование. А в коротковолновом пределе они превращаются в свободно распространяющиеся фотоны, как и должно быть при больших частотах.

#сверхпроводимость

В системах отталкивающихся бозонов иногда встречается переход между моттовским изолятором и сверхтекучестью: когда сила отталкивания на узле U превышает интеграл перескока между узлами J, система находится в состоянии моттовского изолятора, а в обратном случае – в сверхтекучем бозе-конденсированном состоянии.

В этой работе аналогичный переход предсказан для неэрмитовой модели Обри-Андре-Харпера. Это бозоны, движущиеся по одномерной цепочке с несимметричными интегралами перескока, отталкивающиеся на узле и помещенные в периодический потенциал.

Как видно на графиках, с ростом U пропадает недиагональный дальний порядок ρ_ab и появляется заметная щель Δ_ex в многочастичной спектре возбуждений. Это свидетельствует о переходе в состояние моттовского изолятора. А на диаграммах снизу видно, как распространение частиц по цепочке – несимметричное из-за неэрмитовости – идет свободно в сверхтекучей фазе (U=1) и подавляется в фазе изолятора (U=4).

#неэрмитовы_системы #сверхтекучесть

Кстати говоря, сверхтекучесть в работе из предыдущего поста авторы назвали «скин-сверхтекучестью» – по аналогии с неэрмитовым скин-эффектом, при котором из-за несимметричности перескоков частицы скапливаются у одного края образца.

Здесь частицы, как показано черной кривой, тоже скапливаются у правого края, но при этом система в целом сверхтекучая. В этом суть эффекта скин-сверхтекучести.

#неэрмитовы_системы #сверхтекучесть

Авторы этой статьи утверждают, что они распутали сложное поведение оптической проводимости σ(ω) купратных сверхпроводников. Это поведение включает загадочную линейную зависимость скорости рассеяния квазичастиц γ от ω и T, приписываемую квантовому критическому режиму, а также восстановление нормальных фермижидкостных свойств при сильном допировании.

Здесь предложена модель, согласно которой σ(ω) складывается из друдевской части, обусловленной нормальными, делокализованными квазичастицами плотностью n_eff, и лоренцевской части на ненулевой частоте, обусловленной локализованными частицами плотностью n_loc. Поведение n_eff на фазовой диаграмме показано справа.

При росте температуры происходит перенос спектрального веса от локализованных квазичастиц к делокализованным, а при увеличении уровня допирования p – еще и рост общей суммы n_eff+n_loc (как показано стрелочками слева). Это, в совокупности с нормальным поведением делокализованных квазичастиц γ ~ ω², T², объясняет все загадки.

#сверхпроводимость

Соотношение Крамерса-Кронига между амплитудой и фазой коэффициента отражения G(ω) – или любой другой причинной функции отклика – называется также соотношением Боде. Оно полезно на практике, поскольку позволяет восстановить фазу G(ω) по измеряемому коэффициенту отражения по интенсивности |G(ω)|².

Но пользоваться им следует с осторожностью: оно неприменимо, если G(ω) имеет нули, то есть точки полного поглощения, в верхней полуплоскости комплексной плоскости ω. В этом случае соотношение Боде превращается в неравенство: оно дает лишь оценку снизу для фазы φ(ω) = arg G(ω).

На рисунке показан простой пример: G(ω) в виде разности двух лоренцианов на частотах 0.5 и 1 с очень малым затуханием. Функция G(ω) имеет два полюса при ω=1 и ω=0.5 чуть ниже вещественной оси и ноль при ω=1/√2 чуть выше нее. При этом фаза φ(ω), восстановленная из соотношения Боде (черная кривая снизу), по модулю меньше, чем оригинальная фаза функции G(ω), показанная серой кривой.

#фотоника #математика

Еще комментарий насчет соотношения Боде. Любая физическая функция отклика G(ω) должна быть аналитической в верхней полуплоскости комплексной плоскости ω – это следствие принципа причинности. Это означает, что G(ω) не должна иметь в этой полуплоскости полюсов и существенно особых точек. Аналитичность позволяет провести показанное на рисунке контурное интегрирование и вывести соотношения Крамерса-Кронига.

А вот отсутствие нулей G(ω) в верхней полуплоскости принцип причинности никак не гарантирует. Они вполне могут существовать и наблюдаются в эксперименте как частоты ω, на которых отклик системы равен нулю. Почему же они портят соотношение Боде? Потому что оно выводится как частный случай соотношений Крамерса-Кронига для функции ln G(ω).

Если G(ω) аналитична в верхней полуплоскости и не имеет там нулей, то и ln G(ω) тоже там аналитична. Появление же нулей функции G(ω) дает точки ветвления логарифма, делая его неаналитичным.

#фотоника #математика

А вот эксперимент, в котором демонстрировалось нарушение соотношения Боде. Микроволны, поляризованные под углом 45º к вертикали, пропускались через «фотонный кристалл» в виде массива акриловых цилиндров. Коэффициент их пропускания измерялся при чуть меньшем (β = 40º) и чуть большем (β = 50º) углах поворота приемника.

Амплитуда коэффициента пропускания в обоих случаях ведет себя одинаково как функция частоты, как показано синими кривыми. А вот поведение фазы (красные кривые) кардинально различается: при β = 40º она демонстрирует нисходящий участок аномальной дисперсии, а при β = 50º монотонно возрастает.

Здесь мы видим наглядно, как при одной и той же амплитуде функции отклика имеются две различные зависимости фазы от частоты. Только первая из них (при β = 40º) удовлетворяет соотношению Боде. Во втором же случае (при β = 50º) прошедший сигнал запаздывает по фазе сильнее, чем предсказывает это соотношение, из-за наличия у коэффициента пропускания нуля в верхней комплексной полуплоскости частот.

#фотоника

Недавняя работа, вызвавшая множество споров среди астрофизиков, переворачивает наши представления о природе черных дыр и темной энергии. Авторы утверждают, что черные дыры увеличивают свою массу синхронно с расширением Вселенной, а таинственная темная энергия – движущая сила этого расширения – находится как раз у них внутри.

Дело в том, что традиционные решения уравнений Эйнштейна для черных дыр (решения Шварцшильда и Керра) требуют, чтобы метрика пространства-времени на бесконечности становилась плоской. Но в нашей Вселенной это не так из-за ее расширения, поэтому нужно искать другие решения. Одно из них – решение Крокера-Вайнера – подразумевает, что внутри черной дыры отсутствует сингулярность, зато она заполнена энергией вакуума. Масса же ее должна расти как M ~ a³(t), где a(t) – масштабный параметр, описывающий расширение Вселенной. Анализ масс сверхмассивных черных дыр показывает, что степень k, с которой их масса растет с течением времени, действительно очень близка к 3.

#популярное #отвал_башки

Сверхтекучая турбулентность, в отличие от обычной, тесно связана с квантованными вихрями. В трехмерной системе вихревые линии должны либо заканчиваться на краях системы, либо замыкаться в кольцо. При турбулентном течении они образуются в большом количестве и перепутываются в пространстве, давая начало масштабно инвариантному распределению импульсов 1/kⁿ. Оно тесно связано с энергетическим каскадом – процессом передачи энергии от больших масштабов к меньшим.

В этой работе показано, что сверхтекучая турбулентность в атомном газе сильно отличается от таковой в жидком гелии. Если в гелии, как показано на рисунке сверху, вихревые линии заполняют пространство более-менее равномерно, то в атомном газе, из-за его сжимаемости, вихревые линии распределены неравномерно. Как показано снизу, кольцевые линии (синие) расположены вблизи оси атомного облака, движущегося справа налево, а оканчивающиеся на границах линии (красные) тяготеют к его задней части.

#сверхтекучесть #гидродинамика

Это известный эксперимент, в котором впервые был достигнут режим сверхсильной связи между светом и веществом для электронного газа в сильном магнитном поле. Оптические переходы между уровнями Ландау – или циклотронный резонанс – связываются здесь в с электромагнитными модами резонатора в терагерцовом диапазоне.

Как показано на рисунке, резонатор представлен массивом металлических петель. Картины амплитуды электрического поля показывают две моды: m₁ (стандартные колебания в LC-контуре) и m₂ (дипольные колебания вдоль пластин конденсатора). У них не очень высокие добротности в районе 5, но для сверхсильной связи это и не нужно.

На спектре пропускания снизу видны два антипересечения мод m₁ и m₂ с циклотронным резонансом в стопке 4 квантовых ям, энергия которого пропорциональна магнитному полю. Для нижней моды m₁ видно гигантское расщепление Раби. Его отношение к энергии самой моды составляет 0.58, в то время как для режима сверхсильной связи достаточно уже 0.1-0.2.

#уровни_Ландау #фотоника

В электронном газе каждый электрон создает вокруг себя обменно-корреляционную дырку – область пониженной электронной плотности, которую также называют «шубой». Ее обменная часть, или обменная дырка, обусловлена принципом Паули: вероятность обнаружить электрон какой-либо ориентации спина снижается до нуля в точке, где уже есть другой электрон того же спина.

Корреляционная же дырка обусловлена кулоновским отталкиванием и возникает при любых ориентациях спинов. Наглядно это видно на примере двух электронов в атоме гелия. Их спины в основном состоянии антипараллельны, так что обменная дырка отсутствует, а существует только корреляционная дырка. Она не улавливается приближением Хартри-Фока, так что ее можно увидеть, сравнивая точный расчет с хартри-фоковским, как показано снизу.

Можно заметить, что корреляционная дырка слабее обменной: вероятность совместного обнаружения обоих электронов в одной точке проваливается не до нуля, а лишь на 5-10%.

#объяснения #квантовая_механика

Параксиальная оптика сейчас используется для имитации топологических материалов. Распространение света вдоль оптоволоконного массива, вырезанного в прозрачном диэлектрике, описывается аналогом уравнения Шредингера, где показатель преломления играет роль потенциала.

Если массив отповолокон, имеющий форму решетки «пчелиные соты» (синие точки на рисунках) подвергнуть искажению Кекуле (красные точки), то получится фотонный кристалл. Левый рисунок показывает однородное искажение Кекуле, а справа его направление медленно меняется на угол 2π при обходе вокруг центра. Такой дефект решетки создает внутри щели фотонного кристалла связанное состояние для света, чем-то похожее на майорановскую моду.

Такие моды являются неабелевыми энионами – после их перестановки конечное состояние зависит от порядка парных перестановок, или от топологии соответствующей косы. Две перестановки, показанные снизу, дают разные относительные фазы трех мод, локализованных на дефектах: (–,+,–) и (–,–,+).

#топологические_материалы #фотоника

А в этом эксперименте была экспериментально реализована перестановка двух неабелевых энионов, следующая теоретическому предложению, описанному в предыдущем посте. Если, по ходу распространения света, само дефектное искажение Кекуле медленно поворачивается на угол π, это оказывается эквивалентным обходу сидящей на нем моды вокруг бесконечно удаленной «референсной» моды. В итоге наша мода приобретает обменную фазу, зависящую от направления обхода – по или против часовой стрелки.

Авторы взяли одну пару массивов, в которой оба искажения поворачиваются идентично, так что обе моды приобретают одинаковые фазы и в конце интерферируют конструктивно (синие точки). В другой паре массивов искажения поворачиваются в противоположные стороны, так что обменные фазы оказываются разными, и в результате получается деструктивная интерференция (красные точки).

Это пока демонстрация приобретения энионами обменной фазы при одной парной перестановке, но не доказательство их неабелевости.

#топологические_материалы #фотоника

Нарушение критерия сверхтекучести Ландау не обязательно означает реальное исчезновение сверхтекучести. Формально при сверхкритической скорости потока энергии некоторых боголюбовских возбуждений становятся отрицательными, и это приводит к затуханию сверхтекучего потока за счет их массового возбуждения.

Однако в случае сверхтекучих ферми-систем – таких как купратные сверхпроводники или гелий-3 – боголюбовские возбуждения могут просто заполнить те области импульсного пространства, где их энергии отрицательны. Они образуют свои поверхности Ферми и на этом все закончится. Как результат, из-за нарушения критерия Ландау сверхтекучая плотность уменьшается, но не до нуля.

А в этой статье предложено погрузить в сверхтекучий гелий-3 решетку цилиндриков, из-за которой поверхность Ферми боголюбовских возбуждений примет форму, показанную на рисунке. При этом в некоторых местах (в окрестностях точек вырождения) боголюбовские возбуждения будут вести себя как электроны в вейлевских полуметаллах.

#сверхтекучесть