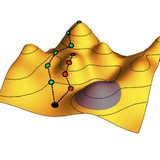
Flow equations – любопытный метод в духе ренорм-группы, позволяющий избавиться от части гамильтониана H₁, отвечающей за взаимодействие, путем перенормировки операторов O в процессе, похожем на непрерывный вариант преобразования Шриффера-Вольфа. Преобразования потока параметризуются величиной l, принимающей значения от 0 до ∞, а показанный на рисунке выбор их генератора η позволяет занулить H₁ в пределе l → ∞.

В этой работе показано, как уравнения потока применяются к задаче о сверхпроводимости. Если стартовать со среднеполевого гамильтониана БКШ, то, как показано на рисунке справа, операторы рождения и уничтожения электронов при этом подвергаются преобразованиям Боголюбова, а в спектре энергий возбуждений ξ постепенно открывается щель.

Авторы при помощи уравнений потока посчитали электромагнитный отклик сверхпроводника с заранее сформированными куперовскими парами и нашли частичный диамагнетизм, существующий в фазе псевдощели выше формальной критической температуры.

#сверхпроводимость

Эта статья Энтони Леггетта довольно часто цитируется в контексте работ о суперсолиде – кристаллической фазе, которая одновременно проявляет сверхтекучие свойства.

Статью довольно тяжело понять, но в целом в ней выводятся верхние и нижние оценки для сверхтекучей плотности ρ_s замкнутой в кольцо системы при T = 0. Результирующая формула, о которой я писал раньше, позволяет понять, будет ли сверхтекучесть существовать в пространственно неоднородной системе – в том числе, и в кристалле.

Автор показывает, что ρ_s > 0, если мы можем пройти по кольцу вдоль замкнутой траектории, на которой волновая функция всегда отлична от нуля. Это интуитивно понятно: в противном случае по обе стороны поверхности Ψ = 0 можно свободно менять относительную фазу, лишая систему глобальной фазовой жесткости. Но такому условию удовлетворяют и многие нормальные системы, поэтому, чтобы ρ_s была не просто ненулевой, а макроскопически большой, система должна обладать недиагональным дальним порядком.

#сверхтекучесть

Энтони Леггетт показывает, что в науке, если у вас нет доказательств, можно иногда ссылаться и на инстинкты.

#цитаты #сверхтекучесть

В этом эксперименте удалось добиться поглощения 95% света в однослойном дихалькогениде переходного металла WS₂. Такое сильное поглощения в настолько тонком материале возможно благодаря сочетанию факторов: экситонному резонансу самого материала и интерференционным эффектам за счет прилегающих слоев нитрида бора и золотой подложки.

На рисунке показана схема структуры и спектр поглощения при температуре 4 K: на нем, в зависимости от уровня допирования, доминируют линии экситона (черная кривая, с самым сильным пиковым поглощением), триона (розовая кривая) и квартона – комплекса трех электронов и одной дырки (зеленая кривая). Что интересно, максимальное экситонное поглощение достигается при повышенной температуре около 110 К – а вовсе не при 4 К, как можно было бы подумать. Как показывают авторы, при этой температуре сравниваются скорости радиационного и нерадиационного распада экситона, и это равенство является условием максимального поглощения.

#экситоны #дихалькогениды_переходных_металлов

Фешбаховские молекулы – это связанные состояния двух атомов, которые можно управляемым образом создавать или разваливать, медленно прогоняя внешнее магнитное поле через резонанс Фешбаха. При этом резонансе длина рассеяния проходит через полюс, говорящий о появлении нового связанного двухчастичного состояния.

Создание бозонных фешбаховских молекул, состоящих из двух одинаковых атомов-фермионов, широко используется для изучения кроссовера БКШ-БЭК. В последние годы научились создавать и гетероядерные фешбаховские молекулы: бозон-бозонную NaCs и фермион-фермионные KRb и NaK. В этом недавнем эксперименте были созданы бозонные молекулы, состоящие из атомов-фермионов ¹⁶¹Dy и ⁴⁰K. За счет магнитных атомов диспрозия и гетероядерности они обладают одновременно магнитным и электрическим дипольными моментами.

На рисунке показан экспериментальный протокол, при котором атомы соединяются в молекулы, после чего оставшиеся несвязанные атомы убираются из облака градиентом магнитного поля.

#атомные_газы #химия

Эффект Капицы-Дирака, предсказанный в 1933 году, заключается в дифракции электронов на достаточно интенсивной стоячей световой волне. Его можно считать аналогом дифракционной решетки, где свет и материя меняются ролями.

В этом эксперименте 2001 года эффект Капицы-Дирака наконец-то был продемонстрирован. Как показано на рисунке, электроны, испускаемые электронной пушкой, фокусировались и пропускались через вакуумную камеру со стоячей волной, образуемой отражением пучка мощного импульсного лазера. В отсутствие лазерного пучка на детекторе-фотоумножителе мы видим одиночное пятно (график слева), а при наличии – уже интерференционную картину (график справа), на которой различимы несколько дифракционных пиков.

Ключевые факторы, позволившие наблюдать эффект – это достаточно мощный лазер (потому что упругое рассеяние электронов на фотонах в свободном пространстве довольно слабое) и высокая степень когерентности электронного и фотонного пучков.

#фотоника #электродинамика

Как говорится, choose your fighter: «в двух экспериментах эффект отклонения электронов световой волной наблюдался, в двух других – нет».

#фотоника #цитаты

В этом эксперименте наблюдалось состояние кластеров 147 атомов натрия с отрицательной теплоемкостью – контринтуитивное явление, при котором добавление энергии к системе делает ее холоднее. Если система находится в контакте с внешним термостатом, то такое состояние не должно существовать из-за своей термодинамической неустойчивости, но в замкнутой системе, которой является небольшой кластер, это вполне возможно.

На графиках показано, как при этом зависят от энергии системы E ее энтропия S, микроканоническая температура T_μ = ∂E/∂S и распределение энергий P_T(E): как видно, S имеет вогнутость, T_m имеет нисходящий участок (а значит, отрицательную теплоемкость ∂E/∂T), а распределение P_T(E) становится двухмодовым, с двумя максимумами вместо одного. Это и наблюдалось в эксперименте, как выделено желтым на диаграмме справа: на ней статистическое распределение энергии кластера определяется по измерению энергий атомов, вылетевших из кластера в результате поглощения фотонов.

#термодинамика

В статье из предыдущего поста наблюдается еще одно аномальное явление: редкий, по нынешним временам, случай, когда авторы статьи в Physical Review Letters не просто уложились в 4 страницы, но даже не использовали этот объем до конца.

#цитаты

Параметрическая накачка (parametric pump) – это явление, при котором частицы перемещаются из одного резервуара в другой не за счет разности их потенциалов (как при протекании обычного электрического тока), а в результате циклических изменений параметров системы. По принципу действия это похоже на насос.

В этой классической работе параметрическая накачка была рассмотрена на языке теории электронного рассеяния в наноструктурах – в формализме Ландауэра-Бюттикера. В этом формализме проводимость G между двумя контактами выражается через элементы матрицы рассеяния S_αβ, где α в β – это квантовые состояния электронов, называемые каналами рассеяния.

Если состояние системы с частотой ω циклически модулируется двумя параметрами X₁ и X₂, то электрический ток I_m, протекающий через контакт m, выражается интегралом вдоль траектории на плоскости (X₁, X₂) от комбинации матрицы S и ее производных по Xᵢ. Это и есть главный результат работы, дающий «геометрическую» интерпретацию процесса накачки.

#наноструктуры

А вот простой пример параметрической накачки. Здесь два параметра X₁ и X₂, которые подвергаются циклической модуляции – это электростатический потенциал U квантовой нити, изменяемый при помощи затворного электрода, и высота γ потенциального барьера поперек нити, которым можно управлять посредством второго электрода.

Циклическое изменение параметров происходит следующим образом:
○ понижаем высоту барьера,
○ понижаем потенциал нити (так что она заполняется электронами),
○ повышаем барьер,
○ повышаем потенциал (из-за чего электроны выталкиваются в правый электрод).

Как видно, принцип перекачки электронов здесь и правда похож на насос, или даже на перистальтику кишечника. Интересно, что перекачиваемый при этом электрический ток I, посчитанный в простейшей одномерной модели, складывается из «классического» вклада (первое слагаемое в формуле на рисунке) и «квантовой» интерференционной поправки (второе слагаемое), осциллирующей в зависимости от длины нити L.

#наноструктуры

Хороший небольшой обзор о принципе максимального калибра, согласно которому существенно неравновесная статистическая система должна описываться распределением траекторий, максимизирующим свою энтропию при наложенных на него условиях, основанных на наблюдаемых данных.

Это довольно мощный принцип. В приближении линейного (по отклонениям от равновесия) отклика из него можно восстановить известные формулы Кубо-Гринвуда, соотношения взаимности Онзагера и принцип минимального производства энтропии Пригожина. Из него можно вывести и динамические законы: уравнение Фоккера-Планка и закон диффузии Фика, причем можно сразу же получить не только среднее значение потока частиц (которое дается оригинальным законом), но и его флуктуации. А для сетей химических реакций и для генных регуляторных сетей по имеющейся обрывочной информации (наблюдаемым потокам веществ, зашумленным траекториям и т.д.) можно проводить наиболее достоверное восстановление сетей и скоростей переходов.

#стохастическая_термодинамика #химия #биология

В этом эксперименте наблюдалось проникновение вихрей внутрь вращающегося бозе-конденсата атомов ²³Na. При этом бозе-конденсированное облако имеет кольцеобразную форму, а проникновение вихрей происходит через сужение кольца (weak link), образованное отдельным вращающимся лазерным лучом.

Такая система похожа по своему гамильтониану на замкнутый в кольцо сверхпроводник, пересекаемый джозефсоновским переходом, где вращение играет роль пропущенного через кольцо магнитного потока. При постепенном увеличении скорости вращения внутрь кольца последовательно проникают 1, 2 и т.д. вихрей (это видно на графиках), а при еще большей скорости вихри образуются и в самой толще кольца.

Это определяется по фотографиям атомного облака, разлетевшегося после выключения удерживающего потенциала, показанным снизу: вихрь внутри кольца дают провал плотности конденсата в центре (по размеру которого можно определить его кратность), а вихри в толще кольца дают провалы, смещенные относительно центра.

#атомные_газы #бозе_конденсация

Кстати, в статье из предыдущего поста хорошо сформулировано, почему вихри образуются не только в самом центре, но и в других местах вращающегося облака бозе-конденсата (в данном случае имеющего форму кольца): причина этого в рассогласовании поля скоростей жидкости v ~ 1/r, совершающей сверхтекучее (то есть безвихревое) течение вокруг центра, и поля скоростей жидкости v ~ r, вращающейся как единое целое вместе с сосудом.

Такие две различающиеся по форме зависимости v(r) могут быть состыкованы в небольшом диапазоне расстояний r до центра облака, то есть в узком кольце. Но в широком кольце или в сплошном облаке энергетическая цена рассогласования становится слишком высокой, и выгоднее становится образовать дополнительные вихри, расположенные уже не в центре, а в других точках облака.

#атомные_газы #бозе_конденсация #сверхтекучесть

Очень интересная статья с теоретическим исследованием того, как электроны, пролетающие мимо поверхности материала, подвергаются эффекту Ааронова-Бома (то есть искажению фазы своей квантовомеханической волны) и декогеренции (подавлению ее способностей к интерференции) за счет электромагнитного отклика материала на сам электрон. В отклик входят и флуктуации в основном состоянии поля, так что этот эффект можно назвать «дифракцией электрона на вакуумных флуктуациях».

Авторы используют два подхода – флуктуационную электродинамику, работающую с электромагнитными функциями Грина, и анализ совместной квантовой эволюции многочастичных состояний электрона и фотонов – получая одинаковые результаты. А еще они хорошо описывают процедуру квантования поля в диссипативной среде.

На графиках показан пример результатов: фазовый сдвиг χ и степень декогеренции –P, приобретаемые электроном, пролетающим путь длиной 1 мкм на расстоянии 10 нм от поверхности золота, как функции его скорости.

#фотоника #электродинамика #отвал_башки

А вот еще интересный пример того, как отклик материала влияет на волновую функцию пролетающего мимо электрона. График слева показывает, как, в зависимости от расстояния до поверхности друдевского металла, меняется фазовый сдвиг, приобретаемый электроном благодаря магнитному полю, генерируемому металлом в ответ на электрическое поле движущегося электрона. Этот фазовый сдвиг (на единицу пути) уменьшается при удалении от поверхности.

Как следствие, если электрон исходно был в состоянии волнового пакета, то он будет искажаться по мере распространения вдоль поверхности металла. Это показано – в координатном и импульсном представлениях – на графиках справа. Чем ближе к металлу, тем быстрее осциллирует волна за счет аарон-бомовского сдвига фаз, а в импульсном представлении это выражается в нарастании вклада высоких импульсов в левом направлении, что можно зарегистрировать в дальнем поле в дифракционном эксперименте.

#фотоника #электродинамика

В двухкомпонентном бозе-конденсате, имеющем взаимодействия между частицами каждой компоненты g₁₁, g₂₂ и межкомпонентное взаимодействие g₁₂, возникают две моды боголюбовских возбуждений: колебания «плотности» и «спина», при которых обе компоненты колеблются, соответственно, в фазе и в противофазе. При (g₁₂)² > g₁₁g₂₂ энергия спиновой моды при малых импульсах становится чисто мнимой, что говорит о неустойчивости основного состояния.

В этой работе утверждается, что в такой ситуации двухкомпонентный бозе-конденсат должен, тем не менее, стабилизироваться в виде самосвязанной капли определенной плотности. На простом языке механизм стабилизации можно объяснить в терминах поправки Ли-Хуанга-Янга к энергии основного состояния взаимодействующего конденсата, показанной на рисунке. А именно, поправка за счет взаимодействия, пропорциональная n⁵ᐟ², при большой плотности n должна скомпенсировать среднеполевой член gn²/2, который в двухкомпонентном случае и является причиной коллапса.

#бозе_конденсация #атомные_газы

Кстати говоря, причину неустойчивости двухкомпонентного бозе-конденсата при (g₁₂)² > g₁₁g₂₂ легко понять и на языке теории среднего поля. В однокомпонентном случае энергия взаимодействия конденсата с самим собой – получаемая, например, из уравнения Гросса-Питаевского – равна gn²/2, где n – его плотность.

В двухкомпонентном случае, где у нас есть взаимодействующие между собой конденсаты с плотностями n₁ и n₂, это выражение обобщается в виде квадратичной формы g₁₁n₁² + g₂₂n₂² + 2 g₁₂n₁n₂. Можно видеть, что при (g₁₂)² > g₁₁g₂₂ эта квадратичная форма уже не является положительно определенной, то есть не имеет глобального минимума, что говорит об отсутствии основного состояния и о неустойчивости однородного конденсата.

Но это лишь приближенная среднеполевая картина – а по-хорошему, нужно учитывать и флуктуации за ее пределами. Вот в статье из предыдущего поста и доказывается, что квантовые флуктуации должны стабилизировать бозе-конденсат, неустойчивый на «классическом» уровне.

#бозе_конденсация #атомные_газы

Любопытная работа, в которой при помощи теории информации исследуется эффективность процесса размешивания жидкостей. Сам процесс показан на рисунке сверху: жидкость помещена в кольцеобразную область, внутренний край которой вращается, увлекая за собой прилегающие слои. Даже в отсутствие вращения (Ω = 0) облако молекул жидкости расплывается за счет диффузии, но вращение (Ω > 0) ускоряет этот процесс.

В качестве меры эффективности размешивания авторы рассмотрели взаимную информацию I между множеством начальных и конечных координат частиц, совершающих диффузионные случайные блуждания в комбинации с дрейфом, обусловленным вращением. На графиках можно видеть, как I падает с течением времени при разных скоростях вращения Ω. Как видно, на малых временах I спадает логарифмически за счет диффузии, но затем этот спад становится экспоненциальным, I ~ exp(–t/τ), с характерным временем τ. В работе даже показано, как, минимизируя это время, можно искать оптимальные протоколы размешивания.

#гидродинамика #информация

Тот факт, что сверхтекучая жидкость не увлекается медленным вращением сосуда, использовался в этом эксперименте для создания чувствительного гирокомпаса. Его устройство показано на рисунке: это тороидальный сосуд со сверхтекучим гелием в виде спирального углубления в кремнии, накрытого сверху каптоновой мембраной и замыкаемого каналом снизу через узкое отверстие в центре.

Принцип действия гирокомпаса основан на том, что сверхтекучий поток гелия, не увлекаемого вращением сосуда, добавляется к осциллирующему потоку, создаваемому колебаниями мембраны (которые возбуждаются электрическим полем). Из-за этого смещается критическая амплитуда колебаний (точка P1 на графике сверху), при которой в узком отверстии происходит проскальзывание фазы, приводящее к диссипации и появлению плато на амплитудной характеристике колебаний. Как показано на графике снизу, зависимость этого смещения от ориентации контура относительно оси вращения Земли, позволяет детектировать последнее, причем с точностью 0.5%.

#сверхтекучесть

Колмогоровская сложность объекта, называемая также алгоритмической случайностью или энтропией Соломоноффа-Колмогорова-Хайтина, определяется как минимальная длина компьютерной программы, способной сгенерировать этот объект. Строго говоря, она невычислима, и ее нахождение для конкретного объекта связано с множеством неопределенностей: какая именно машина выполняет эту программу, каким объемом времени и вычислительных ресурсов она располагает, в каком месте выполнение программы должно останавливаться и т.д. Однако, несмотря на то, что колмогоровскую сложность невозможно найти точно, ее часто можно оценить – сверху, снизу, по порядку величины или с точностью до произвольной аддитивной добавки.

В этой работе Войцеха Цурека колмогоровскую сложность K(s) микроскопического состояния системы s предлагается использовать в качестве алгоритмической энтропии – аналога его термодинамической энтропии. К примеру, если микросостояние s газа в сосуде – это информация о том, какие ячейки пространства (размером с молекулу, на которые разбит сосуд) заняты молекулами газа и каковы значения их скоростей (должным образом дискретизованные), то K(s) будет минимальной длиной компьютерной программы, генерирующей этот паттерн расположения молекул и их скоростей. Все определения энтропии в статистической физике основаны на рассмотрении определенного статистического ансамбля микросостояний (канонического, микроканонического, большого канонического и т.д.), в то время как K(s) определяется для конкретного микросостояния s и не требует никакого ансамбля – в этом ее главное преимущество.

Интересно, что K(s) сильно отличается для случаев типичных и атипичных состояний системы. Атипичное состояние, при котором молекулы, например, выстроились в прямую линию, имеет невысокую колмогоровскую сложность: для «печати» прямой линии достаточно короткой программы. Типичное же состояние газа в сосуде, при котором молекулы расположены, как кажется, совершенно случайно, имеет высокую сложность. Известно, что колмогоровская сложность случайного, или типичного целого числа N приблизительно равна log N, потому что программа, в отсутствие каких-либо закономерностей в записи числа, вынуждена просто напечатать «по памяти» все его log N цифр (показатель логарифма определяется основанием системы счисления).

Так же и для типичного микросостояния термодинамической системы K(s) примерно равна логарифму полного числа доступных микросостояний Γ, и это сближает определение алгоритмической энтропии с больцмановской энтропией S = ln Γ, доказывая ее осмысленность. Более того, автор показывает, что для случая газа в сосуде K(s) типичного микросостояния дается уравнением Сакура-Тетроде – знакомой каждому формулой для энтропии идеального газа S = N[log V + (3/2)log T] + const. Это первый важный результат работы: в типичных случаях алгоритмическая энтропия совпадает с термодинамической.

Второй важный результат работы касается колмогоровской сложности K(E) статистического ансамбля E – набора микросостояний sᵢ, встречающихся с вероятностями pᵢ. Ее можно определить как минимальную длину компьютерной программы, способной напечатать весь набор микросостояний ансамбля с прилагающимися к ним значениями вероятностей. Автор обращает внимание на то, что для типичных ансамблей K(E) должна быть приближенно равна энтропии Шеннона этого ансамбля H = –∑ᵢ pᵢ log pᵢ.

Математически этот результат был доказан еще основателями теории колмогоровской сложности, а объяснить его можно при помощи теории оптимального кодирования: действительно, если микросостояния sᵢ трактовать как набор сообщений, которые мы должны передавать по каналу связи, то средняя длина оптимально закодированного сообщения как раз будет равна H. А длину сообщения можно трактовать как длину компьютерной программы, восстанавливающей каждое микросостояние ансамбля. Таким образом, и для широкого круга различных (как минимум, не патологических) статистических ансамблей алгоритмическая энтропия согласуется с традиционным термодинамическим определением.

#термодинамика #стохастическая_термодинамика #информация #отвал_башки