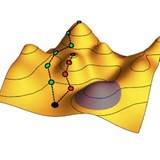
Интересный пример возникновения эффективно однонаправленного распространения электромагнитных волн в простой структуре, взятый из статьи из предыдущего поста и математически схожий со случаем топологического изолятора.

По вертикальному проводу течет ток, модулированный с волновым вектором k_z, а параллельно проводу располагается металлическая поверхность. Три строчки диаграмм показывают случаи различных k_z в единицах волнового вектора волны в свободном пространстве k_0 = ω/c. Яркость и оттенок цвета на диаграммах показывают амплитуду и фазу поля.

По мере того, как k_z приближается к k_0 снизу, происходит нечто интересное. Распределения электрического (E, первый столбец) и магнитного (h, второй столбец) полей демонстрируют распространение поверхностных плазмонов на металле. А если смотреть на поля в базисе правой и левой циркулярных поляризаций (третий и четвертый столбцы), распространение плазмонов оказывается однонаправленным, как на границе топологического изолятора.

#топологические_материалы #плазмоны

С помощью такой картинки я на лекциях пытался объяснить студентам, что фейнмановские диаграммы – это совсем не страшно. Это лишь графические схемы, на которых каждой линии отвечает функция, а все эти функции потом умножаются и интегрируются по импульсам и частотам во внутренних петлях. Но, похоже, эффект оказался обратным...

Некоторые популярные нейросети, занимающиеся генерацией изображений, такие как Midjorney, DALL-E и Stable Diffusion, работают по принципу обратной диффузии.

Этот принцип, основанный на идеях неравновесной термодинамики и методе Монте-Карло, заставляет генерируемое изображение совершать блуждания подобно точке в многомерном пространстве. Обычные случайные блуждания приводят к диффузии, то есть равномерному расплыванию множества точек во все стороны, а здесь они искусно направляются таким образом, чтобы диффузия шла не от осмысленных изображений к случайному шуму, а в обратном направлении – от случайного шума к осмысленному изображению.

В этом посте я пишу о статье 2015 года – одной из основополагающих работ, где был сформулирован метод обратной диффузии. Так что ее будет полезно почитать тем, кто хочет понять, как же работают эти штуки, рисующие картины, которыми уже завалили половину интернета.

https://telegra.ph/Metod-obratnoj-diffuzii-dlya-generativnyh-nejrosetej-07-10

#нейронные_сети #популярное

Красивая иллюстрация инвариантности системы, помещенной в магнитное поле, по отношению к магнитным трансляциям.

Векторный потенциал A(r) магнитного поля зависит от координат и поэтому меняется при сдвигах в пространстве. Если система помещена еще и в периодический потенциал V(r) = V(r + R), то наличие векторного потенциала мешает полному гамильтониану быть периодическим даже с периодом потенциала R.

Тем не менее, давно было замечено, что уравнение Шредингера оказывается инвариантным к магнитным трансляциям: сдвигу в пространстве r --> r + R с одновременным калибровочным преобразованием векторного потенциала. Если «координату» электромагнитного поля, отвечающую векторному потенциалу, обозначить как u, это будет означать, что система инвариантна к сдвигам вдоль наклонных плоскостей в расширенном пространстве (r, u). На рисунке они показаны синим цветом.

#квантовая_механика #уровни_Ландау

Волновая функция квантовой системы, находящейся в связанном состоянии, экспоненциально (или еще быстрее) убывает на больших расстояниях. Поэтому возмущения, накладываемые на систему где-то там, далеко, слабо сказываются на уровнях энергии.

Авторы этой работы посчитали, как будут сдвигаться уровни энергии, если на волновую функцию одномерной квантовой системы далеко от начала координат наложить условия Дирихле, то есть создать для частицы жесткие непроницаемые стенки. Оказывается, что сдвиг энергии, грубо говоря, обратно пропорционален интегралу от 1/ψₒ², где ψₒ – невозмущенная волновая функция. Этот интеграл берется от точки a, находящейся внутри границы и достаточно удаленной и от границы, и от ближайших нулей ψₒ, до положения границы L. Главный вклад в интеграл дается непосредственной окрестностью границы x ≈ L, поскольку именно там ψₒ минимальна.

На картинке показана формула для сдвига энергии в общем случае, когда две границы установлены в точках L₊ и L₋.

#квантовая_механика

В результате оптической накачки в полупроводнике образуются электроны и дырки, которые, после термализации, связываются в экситоны. Если плотность экситонов превышает порог Мотта, их волновые функции настолько сильно перекрываются, а электрон дырочное притяжение настолько сильно экранируется, что экситоны как таковые перестают существовать. Вместо них образуется электрон-дырочная плазма.

Этот эксперимент позволил достичь очень высоких плотностей электронов и дырок, вплоть до 4×10¹⁴ см⁻² в бислое двумерных дихалькогенидов переходных металлов WSe₂/MoSe₂. Оптическая накачка здесь является непрерывной.

Переход Мотта можно обнаружить по спектрам люминесценции: при пересечении плотностью электронов и дырок порога 3×10¹ см⁻² доминирующая спектральная линия, идущая от рекомбинации межслойных экситонов, резко уширяется. А вдобавок появляется линия внутрислойных экситонов MoSe₂, потому что выравниваются края энергетических зон двух соприкасающихся материалов.

#экситоны #дихалькогениды_переходных_металлов

Хорошая иллюстрация из статьи по топологической фотонике, о которой я недавно писал. Она показывает, чем аналитическая функция, удовлетворяющая условиям Коши-Римана, отличается от неаналитической.

Слева показана фаза комплексной функции, полученной в результате суперпозиции 8 плоских волн со случайными амплитудами и различными волновыми векторами. Стрелочки показывают получившиеся вихри и антивихри – точки, при обходе вокруг которых фаза набегает на 2π или –2π.

Справа же показана аналитическая функция переменной z = x + iy. У нее на плоскости нет полюсов и существенно особых точек, а могут быть лишь нули. Вокруг каждого нуля z₀ функция ведет себя как z – z₀, а значит, получает набег фазы 2π при обходе против часовой стрелки.

В итоге, аналитическая функция получается в целом «закрученной» против часовой стрелки, в то время как случайная функция такой преимущественной закрученности не демонстрирует.

#объяснения

Диэлектрическая проницаемость воды ε, как показано на графике, заметно уменьшается при растворении в ней поваренной соли. С 1926-го года это объясняли диэлектрическим насыщением: молекулы воды выстраиваются вокруг ионов в гидратационные оболочки и направляются своими дипольными моментами либо к иону, либо от него (в зависимости от его заряда). Это затрудняет повороты дипольных моментов молекул воды под действием внешних полей, уменьшая ε.

В этой работе при помощи молекулярно-динамических расчетов с нейросетевыми потенциалами модель диэлектрического насыщения была опровергнута. Оказывается, причина уменьшения ε в том, что вмешательство ионов нарушает сетку водородных связей. В чистой воде благодаря этой сетке ближайшие диполи почти сонаправлены и поэтому могут откликаться на внешнее поле коллективно – сильнее, чем по отдельности. В соленой же воде они вблизи ионов могут быть почти антипараллельны (как показано синими стрелками), из-за чего коллективный отклик молекул воды подавляется.

#популярное #химия

Заполнение электронами одночастичных состояний в порядке возрастания их энергий называют принципом Ауфбау. В этой работе показывается, что такой же принцип справедлив и для неэрмитовых систем с комплексными энергиями, только одночастичные заполняются в порядке возрастания вещественных частей их энергий.

Еще один интересный момент показан на рисунке. В одномерной модели Хатано-Нельсона (с несимметричными перескоками вправо и влево) с открытыми граничными условиями частицы скапливаются возле левого края. Диаграммы показывают импульсное (слева) и координатное (справа) распределения в нескольких низших по энергии многочастичных состояниях l для системы 5 фермионов (сверху) или бозонов (снизу).

Видно, что фермионы образуют нечто вроде сферы Ферми (b) и скапливаются вблизи края, насколько позволяет принцип Паули ((a), l=1 для основного состояния). Бозоны же конденсируются как в импульсном пространстве (d), так и в координатном ((c), l=1). Этот факт авторы называют «аномальной конденсацией».

#неэрмитовы_системы

Полюсы и нули функций отклика электромагнитной системы на комплексной плоскости частот ω дают информацию, соответственно, о ее собственных модах и о точках полного поглощения.

Авторы этой статьи обращают внимание на метод численного нахождения полюсов и нулей, основанный на контурном интегрировании по комплексной плоскости. К примеру, мы рассматриваем метаповерхность в виде массива диэлектрических усеченных конусов и, численным решением уравнений Максвелла, находим ее функцию отклика, – например, коэффициент отражения q(ω), – вдоль контура комплексных частот, показанного черными точками. Посчитав интегралы от ωⁿq(ω) с разными степенями n, по ним можно найти положения нулей и полюсов внутри контура – они показаны красными и синими точками. Таким образом, не требуется решать уравнения Максвелла на всей плоскости комплексных частот.

Правда, не стоит забывать, что такой метод применим лишь в том случае, когда оптические константы материалов хорошо определены на комплексных частотах.

#фотоника

Циркулярно поляризованная электромагнитная волна заставляет электроны в облучаемом материале двигаться по кругу. В этом эксперименте показано, что это может создавать магнитное поле до 0.7 Тл, если облучать графеновые нанодиски терагерцовыми импульсами.

Импульс частотой 3.5 ТГц попадает в резонанс с дипольным плазмоном на графеновых дисках диаметром 1.2 мкм. При их облучении циркулярно поляризованным импульсом образуется суперпозиция двух перпендикулярных дипольных плазмонов, сдвинутых по фазе на π/2, то есть циркулярный плазмон с круговым током. Снизу показан результат моделирования магнитного поля, создаваемого таким током.

Его можно обнаружить по аналогу эффекта Фарадея, то есть по вращению плоскости поляризации второго, зондирующего терагерцового импульса, имеющего изначально линейную поляризацию. Даже при не очень большой интенсивности накачки угол вращения достигает 1°, что сравнимо с результатом обычного эффекта Фарадея во внешнем магнитном поле 0.7 Тл.

#плазмоны #графен

Связанные состояния в континууме – сейчас популярная тема, особенно в применении к фотонным кристаллам. Обычно это сугубо одночастичные состояния – решения уравнений Шредингера или Максвелла для одной волны. А в этой работе было численно доказано существование многочастичных связанных состояний в континууме.

Авторы взяли одномерную модель Бозе-Хаббарда с примесью – бозоны, которые перескакивают по цепочке, притягиваются друг к другу, оказавшись на одном узле, а также притягиваются к примеси в центре. На диаграмме показан численно найденный спектр энергий многочастичных состояний E как функция силы межчастичного притяжения U, а цвет дает представление о протяженности волновой функции.

Можно видеть как дискретные связанные (синие), так и континуумы протяженных (зеленых) состояний. А стрелочками указаны связанные состояния, попадающие прямо в полосы континуума. На вставке их можно видеть более четко. Это случай системы 4 частиц, но авторы нашли подобные состояния и в 6-частичной системе.

#квантовая_механика

Занятный расчет сил притяжения между двумя сверхпроводниками, основанный на теории Гинзбурга-Ландау. Авторы рассматривают сверхпроводник, взаимодействующий с электромагнитным полем, и для них выводят эффективный гамильтониан, содержащий энергию поля и сверхпроводящего тока, а также «упругую» энергию, связанную с градиентами электронной плотности.

Взяв два ступенчатых профиля плотности положительно заряженных ионов (черный пунктир), авторы посчитали распределение электронной плотности, минимизирующее полную энергию (сплошная оранжевая линия). Это ситуация двух сверхпроводящих пластин, разнесенных на расстояние L. На графиках справа показаны полная энергия и действующая между пластинами сила как функции L: видно, что между ними существует притяжение, максимальное на расстояниях порядка длины залечивания плотности ξ.

Не знаю, насколько корректен этот расчет с точки зрения теории эффекта Казимира (там много всяких тонкостей), но результат здесь, по крайней мере, получается сходящимся.

#сверхпроводимость

А вот еще интересные соотношения из статьи из предыдущего поста: рассматривая малые возмущения скорости движения электронов сверхпроводника в виде плоской волны, авторы получают их дисперсии, показанные на картинке. Они различаются, в зависимости от поляризации волны.

Продольные колебания – это возмущения плотности. В статическом пределе они спадают в пространстве на масштабах длины залечивания ξ, связанной с лондоновской глубиной проникновения λ_L и длиной когерентности λ_C. В динамике же их дисперсия выходит из плазменной частоты ω_p при k = 0 и становится квадратичной в коротковолновом пределе k → ∞.

В то же время, поперечно поляризованные колебания – это электромагнитные волны, экранированные сверхпроводником. В статике они спадают на расстоянии λ_L – это обычное лондоновское экранирование. А в коротковолновом пределе они превращаются в свободно распространяющиеся фотоны, как и должно быть при больших частотах.

#сверхпроводимость

В системах отталкивающихся бозонов иногда встречается переход между моттовским изолятором и сверхтекучестью: когда сила отталкивания на узле U превышает интеграл перескока между узлами J, система находится в состоянии моттовского изолятора, а в обратном случае – в сверхтекучем бозе-конденсированном состоянии.

В этой работе аналогичный переход предсказан для неэрмитовой модели Обри-Андре-Харпера. Это бозоны, движущиеся по одномерной цепочке с несимметричными интегралами перескока, отталкивающиеся на узле и помещенные в периодический потенциал.

Как видно на графиках, с ростом U пропадает недиагональный дальний порядок ρ_ab и появляется заметная щель Δ_ex в многочастичной спектре возбуждений. Это свидетельствует о переходе в состояние моттовского изолятора. А на диаграммах снизу видно, как распространение частиц по цепочке – несимметричное из-за неэрмитовости – идет свободно в сверхтекучей фазе (U=1) и подавляется в фазе изолятора (U=4).

#неэрмитовы_системы #сверхтекучесть

Кстати говоря, сверхтекучесть в работе из предыдущего поста авторы назвали «скин-сверхтекучестью» – по аналогии с неэрмитовым скин-эффектом, при котором из-за несимметричности перескоков частицы скапливаются у одного края образца.

Здесь частицы, как показано черной кривой, тоже скапливаются у правого края, но при этом система в целом сверхтекучая. В этом суть эффекта скин-сверхтекучести.

#неэрмитовы_системы #сверхтекучесть

Авторы этой статьи утверждают, что они распутали сложное поведение оптической проводимости σ(ω) купратных сверхпроводников. Это поведение включает загадочную линейную зависимость скорости рассеяния квазичастиц γ от ω и T, приписываемую квантовому критическому режиму, а также восстановление нормальных фермижидкостных свойств при сильном допировании.

Здесь предложена модель, согласно которой σ(ω) складывается из друдевской части, обусловленной нормальными, делокализованными квазичастицами плотностью n_eff, и лоренцевской части на ненулевой частоте, обусловленной локализованными частицами плотностью n_loc. Поведение n_eff на фазовой диаграмме показано справа.

При росте температуры происходит перенос спектрального веса от локализованных квазичастиц к делокализованным, а при увеличении уровня допирования p – еще и рост общей суммы n_eff+n_loc (как показано стрелочками слева). Это, в совокупности с нормальным поведением делокализованных квазичастиц γ ~ ω², T², объясняет все загадки.

#сверхпроводимость

Соотношение Крамерса-Кронига между амплитудой и фазой коэффициента отражения G(ω) – или любой другой причинной функции отклика – называется также соотношением Боде. Оно полезно на практике, поскольку позволяет восстановить фазу G(ω) по измеряемому коэффициенту отражения по интенсивности |G(ω)|².

Но пользоваться им следует с осторожностью: оно неприменимо, если G(ω) имеет нули, то есть точки полного поглощения, в верхней полуплоскости комплексной плоскости ω. В этом случае соотношение Боде превращается в неравенство: оно дает лишь оценку снизу для фазы φ(ω) = arg G(ω).

На рисунке показан простой пример: G(ω) в виде разности двух лоренцианов на частотах 0.5 и 1 с очень малым затуханием. Функция G(ω) имеет два полюса при ω=1 и ω=0.5 чуть ниже вещественной оси и ноль при ω=1/√2 чуть выше нее. При этом фаза φ(ω), восстановленная из соотношения Боде (черная кривая снизу), по модулю меньше, чем оригинальная фаза функции G(ω), показанная серой кривой.

#фотоника #математика

Еще комментарий насчет соотношения Боде. Любая физическая функция отклика G(ω) должна быть аналитической в верхней полуплоскости комплексной плоскости ω – это следствие принципа причинности. Это означает, что G(ω) не должна иметь в этой полуплоскости полюсов и существенно особых точек. Аналитичность позволяет провести показанное на рисунке контурное интегрирование и вывести соотношения Крамерса-Кронига.

А вот отсутствие нулей G(ω) в верхней полуплоскости принцип причинности никак не гарантирует. Они вполне могут существовать и наблюдаются в эксперименте как частоты ω, на которых отклик системы равен нулю. Почему же они портят соотношение Боде? Потому что оно выводится как частный случай соотношений Крамерса-Кронига для функции ln G(ω).

Если G(ω) аналитична в верхней полуплоскости и не имеет там нулей, то и ln G(ω) тоже там аналитична. Появление же нулей функции G(ω) дает точки ветвления логарифма, делая его неаналитичным.

#фотоника #математика

А вот эксперимент, в котором демонстрировалось нарушение соотношения Боде. Микроволны, поляризованные под углом 45º к вертикали, пропускались через «фотонный кристалл» в виде массива акриловых цилиндров. Коэффициент их пропускания измерялся при чуть меньшем (β = 40º) и чуть большем (β = 50º) углах поворота приемника.

Амплитуда коэффициента пропускания в обоих случаях ведет себя одинаково как функция частоты, как показано синими кривыми. А вот поведение фазы (красные кривые) кардинально различается: при β = 40º она демонстрирует нисходящий участок аномальной дисперсии, а при β = 50º монотонно возрастает.

Здесь мы видим наглядно, как при одной и той же амплитуде функции отклика имеются две различные зависимости фазы от частоты. Только первая из них (при β = 40º) удовлетворяет соотношению Боде. Во втором же случае (при β = 50º) прошедший сигнал запаздывает по фазе сильнее, чем предсказывает это соотношение, из-за наличия у коэффициента пропускания нуля в верхней комплексной полуплоскости частот.

#фотоника

Недавняя работа, вызвавшая множество споров среди астрофизиков, переворачивает наши представления о природе черных дыр и темной энергии. Авторы утверждают, что черные дыры увеличивают свою массу синхронно с расширением Вселенной, а таинственная темная энергия – движущая сила этого расширения – находится как раз у них внутри.

Дело в том, что традиционные решения уравнений Эйнштейна для черных дыр (решения Шварцшильда и Керра) требуют, чтобы метрика пространства-времени на бесконечности становилась плоской. Но в нашей Вселенной это не так из-за ее расширения, поэтому нужно искать другие решения. Одно из них – решение Крокера-Вайнера – подразумевает, что внутри черной дыры отсутствует сингулярность, зато она заполнена энергией вакуума. Масса же ее должна расти как M ~ a³(t), где a(t) – масштабный параметр, описывающий расширение Вселенной. Анализ масс сверхмассивных черных дыр показывает, что степень k, с которой их масса растет с течением времени, действительно очень близка к 3.

#популярное #отвал_башки