Отличная статья с педагогическим введением в теорию магнетизма. Автор дает обзор основных подходов к описанию того, как магнитные свойства материалов возникают из первых принципов и какими моделями они описываются.

На самом базовом уровне электроны описываются квантовомеханическими моделями или их аппроксимациями – методом функционала плотности, динамической теорией среднего поля, моделью Хаббарда и т.д. Отсюда получаются эффективные спиновые модели, описывающие набор взаимодействующих спинов – такие, как модели Изинга и Гейзенберга. Наконец, на мезо- и макроскопическом уровне от набора спинов на решетке мы переходим к описанию намагниченности как плавно меняющегося в пространстве векторного поля, подчиняющегося уравнению Ландау-Лифшица-Гильберта. Численное решение такого уравнения называется микромагнитным моделированием: оно применяется, когда мы хотим посчитать пространственно неоднородную динамику намагниченности в образцах конечного размера (в том числе, например, перемещение доменных стенок).

Поведение магнитных материалов особенно интересно при наличии трех- или четырехспиновых взаимодействий, а также при наличии существенно анизотропных двухспиновых взаимодействий. Частным случаем последнего является взаимодействие Дзялошинского-Мория, способствующее образованию спиральных и закрученных спиновых текстур. При наличии такого взаимодействия в магнитных материалах могут образовываться устойчивые топологические возбуждения – скирмионы.

#магнетизм #объяснения

Вот как, на базовом уровне, возникает магнетизм.

Система сильно делокализованных (или «обобществленных») электронов с достаточно сильным кулоновским отталкиванием между собой склонна к ферромагнетизму. Действительно, как показано слева, при параллельной ориентации спинов принцип Паули запрещает электронам слишком сильно сближаться – это уменьшает энергию кулоновского отталкивания, а значит, выстраивание спинов параллельно энергетически выгодно.

Если же электроны перескакивают по сильно локализованным орбиталям, то возникает, наоборот, тенденция к антиферромагнетизму. Как показано в центре и справа, антипараллельная ориентация электронных спинов на соседних орбиталях позволяет им совершать виртуальные перескоки, «заходя в гости» друг к другу (что запрещено принципом Паули при параллельной ориентации). Это позволяет волновым функциям электронов распространяться по большей области пространства, понижая их кинетическую энергию – то есть, опять-таки, энергетически выгодно.

#магнетизм #объяснения #твердое_тело

В этой же статье дается хорошее объяснение того, в чем суть подхода DFT+U – метода функционала плотности, дополненного учетом отталкивания электронов на узле U, которое принципиально важно при описании сильно-коррелированных материалов.

В этом методе к энергии многоэлектронной системы добавляются два слагаемых. Первое из них повышает энергию системы на величину U, если два электрона занимают одну и ту же орбиталь (обычно здесь берутся кон-шемовские орбитали). Второе слагаемое – так называемый double counting term – вводится для того, чтобы скомпенсировать двойной учет одного и того же кулоновского взаимодействия. Потому что часть отталкивания на узле U уже содержится в исходном фукционале плотности – ее и нужно убрать.

На рисунке показаны зонная структура и плотность состояний FeO, считаемые в отсутствие (сверху) и при наличии (снизу) корреляционной добавки U. Как видно, при учете отталкивания на узле в спектре открывается щель и материал превращается в изолятор.

#объяснения #сильные_корреляции

А вот хорошая иллюстрация того, как работает взаимодействие Дзялошинского-Мория в магнетиках. К энергии системы оно добавляет слагаемое вида m∙[D∇×m], где m – вектор намагниченности, а матрица D может иметь разный вид, в зависимости от симметрии рассматриваемого материала или гетероструктуры.

На рисунке показаны три распространенных примера матриц D – диагональная, антидиагональная антисимметричная и антидиагональная симметричная. Взаимодействие Дзялошинского-Мория способствует стабилизации скирмионов – топологических возбуждений на фоне общего ферромагнитного выстраивания спинов. Разные структуры матриц D стабилизируют разные виды скирмионов.

Скирмионы не могут просто так «рассосаться» – это потребовало бы макроскопически больших затрат энергии на повороты огромного числа спинов против их ферромагнитного взаимодействия и взаимодействия Дзялошинского-Мория. Поэтому скирмионы могут лишь перемещаются по материалу под действием электрических и магнитных полей.

#магнетизм #объяснения

В этой работе рассмотрен графен в киральной электромагнитной полости – резонаторе, в котором электромагнитные моды правой и левой циркулярной поляризации взаимодействуют с электронами с разными силами или сдвинуты по частоте. При помощи преобразования Шриффера-Вольфа авторы исключили из гамильтониана системы электромагнитные моды и получили эффективный гамильтониан для электронов с модифицированной электронной дисперсией, в которой за счет полости открываются поляритонные щели.

Интересно, что можно рассмотреть не только случай пустой полости, но и полости в фоковском состоянии с определенным числом фотонов. В этом случае возникают топологические поляритоны – расщепления дисперсии с образованием топологически нетривиальных зон по обе стороны щели. А сами расщепленные дисперсии демонстрируют обмен фотонами: как показано на рисунке снизу, при движении вдоль дисперсии меняется среднее число фотонов в поляритонном состоянии, когда мы минуем точку антипересечения.

#фотоника #графен #топологические_материалы

Материал LK-99 нашумел несколько месяцев назад, когда в нем обнаружили сверхпроводимость и магнитную левитацию, существующие при комнатной температуре и исчезающие при температуре 400 К. В этом эксперименте попробовали воспроизвести синтез LK-99 и не обнаружили сверхпроводимости. Аномалии же сопротивления и магнитных свойств при 400 К, похожие на сверхпроводящий переход, оказались обусловлены структурным фазовым переходом в соединении Cu₂S, существующем в LK-99 в виде примеси.

Исследователи изготовили три образца LK-99: S1 и S2 по оригинальной методике и S3 по модифицированной схеме, исключающей подмешивание Cu₂S. Как видно на графиках сверху, S1 демонстрирует аномалии магнитной восприимчивости при 400 К, а S3 – нет. Электрическое сопротивление меняется скачком в S1 и S2 (графики в центре), причем в разную сторону, а S3 остается изолятором.

Графики снизу показывают, что похожие аномалии магнитных свойств и сопротивления наблюдаются в чистом Cu₂S, имеющемся в S1 и S2 в виде примеси.

#сверхпроводимость

Смешное: «хотя почти все эксперименты опровергли существование сверхпроводимости в LK-99, появилось множество теоретических работ, утверждающих, что сверхпроводимость в нем все-таки существует».

#сверхпроводимость #цитаты

Вот одна из ранних теоретических работ про спонтанное нарушение симметрии в PT-симметричной оптической системе при переходе через исключительную точку.

Авторы рассматривают плоский волновод, состоящий из областей с комплексно сопряженными показателями преломления n = n_w ± iαλ/4π. На графиках показано, как вещественная и мнимая часть эффективного показателя преломления N, с которым мода распространяется вдоль волновода, зависит от степени накачки в одном слое и утечки в другим α.

При α ниже критического значения имеются две моды с симметричным и антисимметричным профилями поля, как показано левой диаграммой снизу. Вдоль волновода эти моды не растут и не затухают (N вещественно), но распространяются с разными скоростями. При α выше критического значения PT-симметрия нарушается: как показано правой диаграммой снизу, одна мода смещается в область с потерями и становится затухающей, другая смещается в область с накачкой и растет по амплитуде при движении вдоль волновода.

#неэрмитовы_системы #электродинамика

Из статьи по PT-симметричной оптической системе:
«На первый взгляд, перебор всех возможных вариантов расчета мощности переданного сигнала, показанных на рисунке, неоправданно усложняет задачу. Но это не так – сами посмотрите, все становится очень просто и понятно...»

#неэрмитовы_системы #электродинамика #цитаты

Динамика электронов, заселяющих плоскую энергетическую зону, определяется ее квантовыми геометрическими свойствами. Потому что кинетическая энергия здесь равна нулю и квантовая геометрия, зависящая от структуры волновых функций – единственное, что не дает электрону мгновенно изменять свое квантовое состояние без затрат энергии.

В этой работе рассмотрено образование экситонного диэлектрика в том случае, когда зона проводимости и валентная зона являются плоскими и обладают нетривиальной квантовой геометрией. Авторы показывают, что волновая функция относительного движения электрона и дырки в составе экситона наследует эту нетривиальную геометрию: например, она обладает завихренностью, равной разности чисел Черна зоны проводимости и валентной зоны (пример такой завихренной волновой функции показан на рисунке). Конденсат таких плоскозонных экситонов должен демонстрировать холловский фототок (то есть квадратичный оптический отклик), пропорциональный этой завихренности.

#экситоны #топологические_материалы

Обзорная статья о физике квантованных вихрей в сверхпроводниках. Такие вихри мешают протеканию стабильных незатухающих токов, потому что на каждый вихрь со стороны тока действует сила Магнуса, из-за чего он начинает двигаться по сверхпроводнику. Поскольку внутри вихря имеется нормальная фаза, ее протаскивание через беспорядок приводит к потерям энергии на диссипацию и к затуханию сверхпроводящего тока.

Чтобы вихри не ползли по образцу, их нужно закреплять (пининговать) примесями, дефектами или специальными неоднородностями. Если неоднородность достаточно крупная, она может в одиночку удержать вихревую линию, а мелкие дефекты могут делать это коллективно. Иногда в сверхпроводниках делают специальные массивы отверстий, чтобы ловить в них вихри и не давать им перемещаться.

В связи с этим, моделирование поведения вихрей в заданной геометрии системы и при заданной конфигурации дефектов – это важная задача, для решения которой используют разные вычислительные методы, включая машинное обучение.

#сверхпроводимость

Принцип максимальной энтропии (MaxEnt), о котором я писал раньше, утверждает, что при наличии фрагментарной информации о статистическом распределении наиболее правильным, или несмещенным его выбором будет тот, который максимизирует энтропию Шеннона этого распределения при условии правильности имеющейся о нем информации (например, о среднем значении или дисперсии). Существует аналог этого принципа, но формулируемый для траекторий, через которые система должна проходить в течение определенного времени, называемый принципом максимального калибра (principle of maximum caliber, MaxCal).

Принцип MaxCal позволяет восстановить неизвестное нам распределение p[x(t)] траекторий x(t), через которые проходит система: если у нас имеется какая-то информация об этих траекториях или накладываемые на них ограничения, то наиболее правильным выбором распределения p[x(t)] будет такой, при котором выполняются эти ограничения и одновременно достигает максимума энтропия S = –∫Dx(t) p[x(t)] ln p[x(t)], считаемая как функциональный интеграл по всем траекториям x(t). Логика рассуждений, лежащая в основе этого принципа, такая же, как и в случае MaxEnt: если энтропия не максимальна, это значит, что при формулировке нашей гипотезы насчет распределения p[x(t)] мы, в неявном виде, учли какую-то дополнительную информацию помимо уже имеющихся фактов, исказив его форму.

Важно понимать, что принцип максимального калибра, как и принцип максимальной энтропии – это не просто философский принцип «максимизации степени нашего незнания о том, что мы действительно не знаем», а вполне рабочий инструмент, позволяющий делать проверяемые предсказания. К примеру, по имеющейся информации о траекториях статистической системы мы можем, следуя этому принципу, найти распределение p[x(t)], а потом по этому распределению посчитать другие наблюдаемые величины, характеризующие поведение системы.

Вот один из примеров работы принципа MaxCal: представим, что система с течением времени может перескакивать между набором дискретных состояний {u}, и единственное, что известно о статистике ее траекторий – это полное число переходов Nᵤᵥ, совершенных за все время из каждого состояния u в каждое состояние v в неизвестные нам моменты времени. В этом случае распределение траекторий u(t), максимизирующее энтропию при заданных Nᵤᵥ, задается марковским процессом, то есть уравнениями вида dpᵤ/dt = ∑ᵥWᵤᵥpᵥ(t) для вероятностей pᵤ(t) нахождения системы в состоянии u в каждый момент времени. Здесь мы видим, как можно обосновать часто используемое допущение о марковском характере случайных процессов: для широкого круга постановок задач это допущение действительно будет наиболее «честным» и несмещенным.

Больше о принципе максимального калибра можно узнать в этом обзоре, где подробно обсуждаются принципы MaxEnt и MaxCal, а также некоторые их реальные применения.

#стохастическая_термодинамика #информация #объяснения

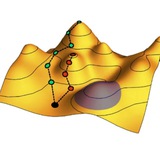
А вот эксперимент, в котором принцип максимального калибра (MaxCal) был проверен на работоспособность.

Кварцевая бусинка, плавающая в жидкости, удерживалась в двухъямном потенциале, созданном лазерными лучами. Как показано на рисунке, в ходе своего броуновского движения она случайно перескакивает между двумя ямами, так что можно измерить средние по большому числу временных шагов количества переходов из ямы a в яму b и обратно (<N_ab> и <N_ba>), а также количества временных шагов, в течение которых частица остается в прежней яме (<N_aa> и <N_bb>). По этим измеренным средним авторы подобрали модель кинетики частицы, следуя принципу MaxCal, и посчитали другие, более сложные статистические характеристики процесса.

На диаграммах показано сравнение этих величин, предсказываемых принципом MaxCal (по горизонтальным осям) и измеренных в эксперименте (по вертикальным осям). Эти величины включают в себя кумулянты высших порядков N_ab и N_ba, а также время нахождения частицы N_B в яме b.

#стохастическая_термодинамика

А эта статья – большая апология принципа максимального калибра, который предлагается в качестве основополагающего принципа, на котором должна строиться термодинамика существенно неравновесных процессов.

В равновесной термодинамике (панель (a) на рисунке) мы всегда находимся в термодинамическом равновесии, когда состояние системы описывается статистическим ансамблем, выводимым из соображений максимизации энтропии. Существующая неравновесная термодинамика описывает малые отклонения от равновесия в виде гауссовых флуктуаций (b), происходящие в системе, взаимодействующей с равновесными резервуарами.

В принципе, можно отходить и сколь угодно далеко от равновесия, если процесс стартует с равновесного состояния – сейчас это описывается многочисленными флуктуационными теоремами. Для процессов же, с самого начала находящихся далеко от равновесия (d), пока не существует общепринятого термодинамического аппарата – и он может быть основан на принципе максимального калибра.

#стохастическая_термодинамика #термодинамика

Эллиот Либ (Elliott Lieb) – математик и физик-теоретик, доказавший множество важных теорем, накладывающих точные ограничения на поведение физических систем. Эта книга представляет сборник его избранных работ, касающихся физики конденсированной материи.

Вот сильно неполный список задач, которым посвящены эти работы:
• Бозонизация фермионных систем и, в частности, точное решение одномерной модели Хаббарда.
• Доказательство того, что модель Хаббарда с притяжением должна иметь в основном состоянии нулевой спин при любом четном числе электронов.
• Знаменитая теорема Либа-Шульца-Маттиса о том, что система спинов, обладающая инвариантностью относительно вращений и трансляций, с полуцелым спином, приходящимся на одну ячейку, должна либо быть бесщелевой, либо спонтанно нарушать какую-либо из симметрий (т.е. в ней должны устанавливаться ферромагнетизм, антиферромагнетизм или иной тип магнитного упорядочения), либо быть щелевой спиновой жидкостью.
• Установление шахматного узора намагниченности в модели Фаликова-Кимбала.
• Доказательство того, что переход Пайерлса в одномерной цепочке – это единственное нарушение симметрии, способное понизить энергию системы при гармоническом взаимодействии атомов и линейной зависимости интегралов электронных перескоков от расстояния.
• Доказательство того, что энергия основного состояния системы электронов – одномерной или антиферромагнитной гейзенберговской – при заданном спине S удовлетворяет соотношению E(S) ≤ E(S+1), то есть наименьшие спины являются наиболее выгодными по энергии.
• Доказательство существования лазерной генерации в модели Дике.
• Доказательство стабильности полярона, то есть ограниченности его энергии снизу, при сколь угодно большой константе электрон-фононного взаимодействия.
• Доказательство того, что в главном порядке плотности ρ энергия N взаимодействующих бозонов в двух измерениях дается выражением E = 4πNρ/ln(ρa²), где a – длина рассеяния.
• Доказательство того, что уравнение Гросса-Питаевского для взаимодействующих бозонов становится точным в пределе N → ∞, а → 0, Na = const.
• Строгое доказательство существования бозе-конденсации в основном состоянии трехмерной системы взаимодействующих бозонов при некоторых ограничениях на потенциал взаимодействия.
• Доказательство того, что бозе-конденсация сохраняется в слабом периодическом потенциале, но исчезает при слишком большой его амплитуде.
• Расчет энтропии квадратного и кубического спинового льда.
• Операторная алгебра Темперли-Либа, которая была разработана для анализа спинового льда, а затем нашла применения в теории перколяции, задачах раскрашивания графов и других задачах геометрии и топологии.
• Альтернативное точное решение двумерной модели Изинга – физически более прозрачное, чем оригинальное решение Онзагера.

#твердое_тело #магнетизм #бозе_конденсация

Вот это очень интересная работа, в которой решена проблема 40-летней давности о том, как правильно выводить эффективно классическую динамику для подсистемы квантовой системы.

Как известно, квантовые эффекты пропадают, если стремить постоянную Планка ħ, задающую квантовый масштаб действия, к нулю. По этой причине предел ħ → 0 называется классическим пределом. Восстановление классического предела работает и на языке уравнений. Например, состояние квантовой системы можно описывать при помощи функции Вигнера W(q, p) – матрицы плотности ρ(q + r/2, q – r/2), подвергнутой преобразованию Фурье по переменной r с импульсом p. Функция Вигнера подчиняется уравнению, которое в пределе ħ → 0 превращается в классическое уравнение Лиувилля ∂W/∂t = {Н,W} со скобками Пуассона.

Важное свойство уравнения Лиувилля в том, что оно сохраняет положительную определенность функции Вигнера – таким образом, ее можно уже интерпретировать как плотность распределения состояния классической статистической системы по фазовому пространству. Исходное же квантовое уравнение для W при конечных ħ не сохраняет ее положительную определенность, делая невозможным описание динамики на классическом языке.

Однако описанная процедура получения классического уравнения для функции Вигнера в пределе ħ → 0 не работает, когда мы хотим сделать эффективно классической лишь одну из двух взаимодействующих подсистем, оставив другую квантовой. А такая процедура может быть востребованной для ряда задач, начиная с первопринципного обоснования элементарной молекулярной динамики, где движение атомных ядер считается классическим, а поведение электронов существенно квантовым. Проблема состоит в том, что даже если для «классической» подсистемы взять предел ħ → 0, так что ее внутренняя динамика будет описываться уравнением Лиувилля, сохраняющим положительную определенность функции Вигнера W, за счет взаимодействия с оставшейся «квантовой» частью системы между подсистемами постоянно генерируется квантовая запутанность. Как следствие, если в какой-то момент времени W классической подсистемы является неотрицательной, спустя небольшое время она теряет это свойство.

Для решения этой проблемы авторы предлагают учитывать декогеренцию, обусловленную взаимодействием классической подсистемы с окружением – в контексте многих задач она действительно играет важную роль при установлении классического предела. Технически это можно сделать, проецируя W(q, p) через равные промежутки времени τ на базис когерентных состояний в пространстве (q, p). Такое проецирование размазывает W(q, p) на мелких масштабах, устраняя участки ее отрицательных значений.

Оказывается, правильный классический предел для подсистемы получается при ħ → 0, τ → 0, ħ/τ = const, то есть когда мы устраняем квантовые эффекты, но и делаем характерное время потери когерентности τ бесконечно малым. Отношение же E_f = ħ/τ, имеющее смысл характерной энергии квантовых флуктуаций системы за счет окружения, должно оставаться при этом постоянным. Уравнение для функции Вигнера классической части системы и эффективный гамильтониан для оставшейся квантовой части системы имеют довольно громоздкий вид, но, тем не менее, обладают всеми нужными свойствами.

#квантовая_механика #открытые_квантовые_системы #отвал_башки

Как я писал выше, система уравнений, описывающих классическую динамику одной подсистемы и связанную с ней квантовую динамику другой подсистемы, в общем виде выглядят довольно сложно.

Но авторы рассмотрели пару простых примеров, основанных на гармонических осцилляторах. Оказывается, в пределе ħ → 0, τ → 0, E_f = ħ/τ = const функция Вигнера W классической подсистемы подчиняется уравнению Лиувилля с дополнительной квантовой диффузией. В простейшем случае оно выглядит как
∂W/∂t = {Н,W} + E_f [∂²W/∂q² + ∂²W/∂p²]/2.
Первое слагаемое в правой части – это скобки Пуассона, отвечающие за классическую динамику, а второе слагаемое придает функции W дополнительную диффузию вдоль переменных q и p, интенсивность которой пропорциональна E_f. Это квантовая диффузия, обусловленная взаимодействием системы с окружением.

Интересно, что такая форма уравнения для W согласуется с теоремой Павулы (Pawula theorem), согласно которой для сохранения положительной определенности функции W уравнение для нее не должно содержать производных более высокой степени, чем вторая. Иными словами, общее уравнение, сохраняющее положительную определенность, должно иметь вид уравнения Фоккера-Планка. Производные первого порядка по q и p здесь имеются в скобках Пуассона, второго порядка – в диффузионном члене. Исходное квантовое уравнение для W содержит производные всех порядков до бесконечности, поэтому положительную определенность не сохраняют.

Кстати говоря, оставшаяся квантовая часть системы подчиняется динамике, параметры которой зависят от состояния классической системы. Здесь интересен предел E_f → 0, отвечающий исчезающе слабой диффузии. Авторы обнаружили, что возможны два варианта поведения квантовой системы в этом пределе. В первом случае возникает когерентный контроль над квантовой системой со стороны классической: примерно как в традиционной квантовой механике, где классическое окружение выступает «сценой», на фоне которой развивается унитарная динамика квантовой системы (например, квантовая частица движется в потенциале, заданном внешними классическими силами). Во втором случае квантовая система подвергается быстрой декогеренции и ее состояние коллапсирует к вектору, определяемому текущим состоянием квантовой системы. Это случай квантового эффекта Зенона – «замораживания» динамики квантовой системы под сильным влиянием измерительного прибора. Но при каких условиях реализуется каждый из двух сценариев, в общем случае пока непонятно.

#квантовая_механика #открытые_квантовые_системы #отвал_башки

Когерентный идеальный поглотитель (или антилазер) – это оптическая система, которая, за счет комбинации диссипации и интерференции, полностью поглощает определенную моду электромагнитного излучения. Его можно рассматривать как обращение во времени лазера, работающего на пороге генерации еще в линейном режиме и испускающего излучение в эту моду.

Понять формирование идеального поглощения можно на языке S-матрицы оптической системы, элементы которой Sᵤᵥ(k) дают отношение амплитуды уходящей на бесконечность u-й моды с волновым числом k и частотой ω = ck к амплитуде падающей на систему v-й пространственной моды с той же частотой. Лазерная генерация возникает, когда при постепенном усилении накачки один из полюсов S-матрицы поднимается из нижней полуплоскости Im k < 0 и достигает вещественной оси.

Аналогично, если, при введении в систему диссипации, один из нулей S-матрицы спускается с верхней полуплоскости Im k > 0 до вещественной оси, возникает когерентное оптическое поглощение.

#электродинамика

В этой работе впервые было введено понятие когерентного идеального поглотителя (обращенного во времени лазера). Авторы придумали простой пример такой системы, основанной цилиндрическом куске кремния, помещенном внутрь оптоволокна.

На диаграмме сверху показаны положения нулей (они изображены синими крестами и красными кругами – это два способа расчета) и полюсов (синие треугольники и красные квадраты) S-матрицы на комплексной плоскости k. Как видно, один из нулей находится на вещественной оси, что отвечает когерентному идеальному поглощению. Оно проявляется как провал до нуля интенсивности рассеянной волны при λ = 945.3 нм в канале симметричных мод (синяя кривая снизу).

Что интересно, идеальное поглощение возникает здесь именно для симметричной моды: это означает, что две волны, падающие синфазно слева и справа на кремниевый цилиндр, за счет деструктивной интерференции взаимно гасят свое прохождение и отражение, запирая излучение внутри цилиндра до тех пор, пока оно полностью не поглотится.

#электродинамика

При ненулевом сверхпроводящем токе дисперсия боголюбовских квазичастиц в сверхпроводнике искажается за счет эффекта Доплера: энергия возбуждения частиц, движущихся вдоль тока, снижается, а против тока – повышается. При сверхкритическом токе доплеровское искажение становится настолько сильным, что для боголюбовских квазичастиц образуются поверхности Ферми, как показано на рисунке слева.

В этом эксперименте впервые зарегистрировано наличие таких поверхностей Ферми. Они обнаружены на поверхности пленки топологического изолятора Bi₂Te₃, где сверхпроводимость наводится эффектом близости со стороны прилегающего NbSe₂, а ток запускается магнитным полем. Картины интерференции квазичастиц (показанные справа), которые получаются преобразованием Фурье измеренной локальной плотности состояний, дают информацию об упругом рассеянии частиц на примесях с различными импульсами рассеяния. На них видны сгущения на волновых векторах, соединяющих участки поверхностей Ферми боголюбовских квазичастиц.

#сверхпроводимость

В этой статье Николааса Гугенгольца 1965 года дается обзор сложившейся на тот момент квантовой многочастичной теории конденсированной материи, в том числе аппарата функций Грина, применяемого к таким задачам, как бозе-конденсация и сверхпроводимость.

Среди прочего, автор описывает разложение Бракнера-Голдстоуна – ранний вариант диаграммной техники, в котором энергия основного состояния взаимодействующего электронного газа раскладывалась в ряд теории возмущений. На рисунке показаны поправки к энергии 1-3 порядков и отвечающие им диаграммы. Можно заметить, что поправка E₀⁽³⁾ состоит из регулярного (имеющего 3 энергетических знаменателя) и нерегулярного (являющегося произведением поправок 1-го и 2-го порядков) слагаемых, а диаграммы для нее содержат одну несвязную – распадающуюся на два отдельных куска. Бракнер, Голдстоун и Гугенгольц доказали, что в полном ряде теории возмущений вклады всех несвязных диаграмм сокращают вклады нерегулярных слагаемых, оставляя только связные регулярные диаграммы.

#твердое_тело