Авторы статьи про фотомолекулярный эффект предполагают, что открытый ими эффект может объяснить часто наблюдаемое явление, когда «солнце развеивает туман».

Действительно, капельки воды, будучи почти прозрачными, сами по себе слишком слабо поглощают свет, чтобы заметно нагреваться и испаряться в солнечных лучах. Другое дело – фотомолекулярный эффект, при котором электрическое поле световой волны вырывает кластеры молекул воды с ее поверхности. У мелких капелек тумана отношение площади поверхности к объему очень велико, поэтому поверхностные эффекты должны идти весьма интенсивно.

#электродинамика #химия #цитаты

Исключительная точка неэрмитовой системы – это точка пространства параметров, в которой происходит бифуркация собственных значений гамильтониана, а поведение системы качественно меняется. В качестве неэрмитовой можно описывать систему, взаимодействующую с термостатом и передающую ему энергию в форме релаксации.

Но ведь совокупность системы и термостата описывается эрмитовым гамильтонианом – как здесь возникает исключительная точка, когда размер термостата стремится к бесконечности? В этой статье демонстрируется процесс эффективной «потери эрмитовости» на языке величины D₁₂(T) – это дисперсия отношения амплитуд колебаний двух осцилляторов, из которых состоит система, считаемая в среднем по начальным условиям и достаточно большому времени T.

На графиках видно, как она ведет себя похожим образом при пересечении исключительной точки в неэрмитовой (слева) и в эрмитовой (справа) системах. Получается, эта величина действительно улавливает нечто общее для открытой и замкнутой квантовых систем.

#неэрмитовы_системы

Ну вот, теперь постмодернизм добрался и до термодинамики... 😐

#термодинамика #цитаты

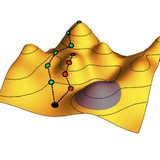
Хороший курс лекций по современной термодинамике и теории стохастических процессов. Главный фокус здесь делается на теории марковских случайных процессов – случайного блуждания либо в пространстве (это случай броуновского движения), либо на множестве дискретных состояний системы (а это уже популярный метод описания классических статистических систем и вывода законов стохастической термодинамики, которым они подчиняются).

Еще довольно неплохо и подробно, начиная с самых основ, излагается теория сетей химических реакций, появившаяся в последние годы и уже оказавшаяся полезной для описания сложных и разветвленных химических процессов (в том числе метаболизма) и их термодинамических и статистических свойств.

Уделяется место и теории мартингалов – определенных характеристик случайных процессов, позволяющих рассчитывать всякие полезные вещи типа времени достижения (first passage time).

#термодинамика #стохастическая_термодинамика

Пытаемся поймать на удочку Пуассона... Или, если не получится, то хоть что-нибудь пуассонообразное.

#стохастическая_термодинамика #цитаты

Как известно, на границе двух топологических изоляторов, отличающихся значениями топологических инвариантов, внутри энергетической щели должны существовать краевые состояния. А здесь показано, что это не совсем так: сказанное выше справедливо только в том случае, если в области плоскости, занимаемые каждым из двух изоляторов, можно поместить сколь угодно большие круги.

Первые три примера на рисунке удовлетворяют этому условию, а четвертый нет: в красную область, имеющую форму ленты, произвольно большие круги не влезут. В четвертом случае краевые состояния уже не будут полностью заполнять всю щель.

Авторы математически доказывают более общий результат: если максимальный размер круга равен R, то вблизи каждого уровня энергии внутри щели существует другой уровень энергии на расстоянии, не большем α ln R/R, где α – некоторая константа. Таким образом, чем больше размер куска топологического изолятора R, тем плотнее спектр краевых состояний внутри щели.

#топологические_материалы

Кстати говоря, круги, о которых шла речь в предыдущем посте – это не совсем круги, а то, что называется термином ℓ₁-ball, то есть круги по модулю ℓ₁. Обычные, традиционные круги – это, с точки зрения математики, круги по модулю ℓ₂.

На рисунке показаны примеры разных кругов. В целом, круг радиуса R по модулю ℓᵦ определяется как |x₁|ᵝ + |x₂|ᵝ + … = Rᵝ. При β = ∞ такой обобщенный «круг» и вовсе превращается в квадрат.

#математика #геометрия

Вот это крутая работа, в которой придуман метод экспериментального восстановления трехмерной структуры кристалла по одному-единственному (и очень короткому, длительностью 25 фс) импульсу, испускаемому рентгеновским лазером на свободных электронах.

Метод основан на детектировании линий Косселя. Они получаются следующим образом: падающий на кристалл рентгеновский импульс возбуждает его электроны, которые испускают вторичное рентгеновское излучение. Это вторичное излучение интерферирует с собой же, рассеянным на кристаллической решетке, и результат интерференции дает на экране линии Косселя – примеры показаны на рисунке справа.

Важно, что эти линии, в отличие от обычных рефлексов Лауэ, несут в себе информацию не только об амплитудах, но и о фазах пространственных фурье-гармоник электронной плотности. Поэтому их достаточно для полного восстановления трехмерной картины электронной плотности в кристалле, пример которой для арсенида галлия показан снизу.

#твердое_тело

Первое правило фемтосекундной кристаллографии: «проводите измерения до разрушения образца (не после!)»

#цитаты #твердое_тело

А вот иллюстрация, демонстрирующая актуальность первого правила фемтосекундной кристаллографии.

На образец арсенида галлия попал единственный 25-фемтосекундный импульс рентгеновского лазера на свободных электронах, что вызвало испарение материала в самом месте попадания и разрушение кристаллической структуры вокруг.

Именно поэтому столь важно уметь анализировать образец с первого же попадания импульса: рассеяние рентгеновских лучей, дающее информацию о структуре кристалла, происходит очень быстро, пока его атомы еще не успели раскачаться и материал не испарился.

#цитаты #твердое_тело

Теории скрытых параметров – это попытка расширить квантовую теорию, получив более точную модель. С практической точки зрения это означает, что знание не только волновой функции системы, но и дополнительных скрытых параметров должно давать возможность получать более точные – то есть менее случайные – предсказания результатов измерений, проводимых над квантовой системой.

Хотя локальные теории скрытых параметров были опровергнуты в знаменитых экспериментах Алана Аспе, остаются, в принципе, возможности и других расширений квантовой механики. В этой работе доказывается, что, никакие расширения квантовой механики, увеличивающие ее предсказательную силу, невозможны – при выполнении некоторых разумных условий. Иными словами, существующая квантовая механика – это наиболее полная теория. Хотя она не дает, во многих случаях, предсказаний того, какой именно результат квантового измерения будет получен, а предсказывает лишь вероятности получения разных результатов, никакими расширениями квантовой механики невозможно получить более точные предсказания.

Если квантовая система находится в каком-то чистом состоянии с заданной волновой функцией, то при различных установках измерительного прибора A мы можем получать случайные результаты измерений X с вероятностью P(X|A). К примеру, X = ±1/2 – это случайно получаемые проекции спина на направление, задаваемое набором параметров A. Первое из упомянутых выше условий, которое должно выполняться – это условие свободы выбора, то есть возможность свободного, не зависящего от состояния квантовой системы, выбора параметров измерений A. Как и в экспериментах по исключению лазейки свободного выбора, это можно сделать, выбирая A случайно в точке, отделенной пространственноподобным интервалом от точки приготовления квантового состояния системы. Тогда никакие скрытые сигналы от измеряемой системы, распространяющиеся не быстрее скорости света, не смогут повлиять на наш выбор A.

Второе условие – это справедливость стандартной квантовой механики. Оно вполне логично: ведь мы пытаемся расширить квантовую механику, а не опровергнуть ее, поэтому на правах, гипотетически, менее точной теории, она тоже должна работать. Авторы доказывают, что при выполнении этих двух условий никакая дополнительная информация Ξ, даваемая «расширенной» теорией, не может улучшить точность предсказанной статистики P(X|A) при заданной волновой функции системы. Математически это можно представить так: статистика X зависит от Ξ только через посредство величины A. То есть информация Ξ, в принципе, может повлиять на A, которая, в свою очередь, может повлиять на X, но непосредственно, в обход величины A, информация Ξ не может повлиять на статистику X. Таким образом, знание Ξ не дает нам никакой дополнительной полезной информации, помимо уже имеющегося у нас знания параметров измерений A.

Насколько я понял, доказательство основано на моногамии квантовых корреляций: если представить, что мы проводим измерения над максимально запутанной парой квантовых подсистем, то их состояние не может быть скоррелировано ни с какими другими дополнительными системами (которые, гипотетически, могут нести информацию Ξ). Поэтому не существует никакой дополнительной информации Ξ, которая может быть связана с результатами измерений над максимально запутанными подсистемами. Затем этот результат распространяется уже на обычные квантовые системы, не находящиеся в максимально запутанном состоянии.

Как и в случае лазейки свободы выбора, доказанная в этой работе теорема не исключает сценария полного детерминизма: если предположить, что вся история нашей Вселенной предопределена, то знание параметров этой предопределенности Ξ позволит предсказать результаты всех квантовых измерений, которые когда-либо будут проведены. Но в этом случае нарушается условие свободы выбора, потому что выбор параметров измерений A тоже будет предопределен и уже не может считаться свободным. Другие варианты нелокальных скрытых параметров – например, теория де-Бройля-Бома – также нарушают это условия.

#квантовая_механика #отвал_башки

Марковские модели популярны для описания термодинамических процессов. В таких моделях мы предполагаем, что система может находиться в одном из дискретных состояний, между которыми происходят случайные переходы с матрицей скоростей W. Вероятности нахождения системы в состояниях с разными энергиями εᵢ меняются с течением времени, как показано формулой (1) на рисунке.

Если система находится в контакте с термостатом, то именно он индуцирует переходы между состояниями. Тогда элементы матрицы W связаны условием детального равновесия (2), в котором фигурирует обратная температура термостата β.

Если же система находится в контакте с несколькими термостатами разных температур, скорости индуцированных ими переходов принято складывать, как показано формулой (3). Автор этой работы показывает, что это неправильно: если каждая из матриц Wᵘ подчиняются своему условию детального равновесия со своей обратной температурой βᵤ, то система уравнений (1) становится внутренне противоречивой.

#стохастическая_термодинамика

Отличная статья с педагогическим введением в теорию магнетизма. Автор дает обзор основных подходов к описанию того, как магнитные свойства материалов возникают из первых принципов и какими моделями они описываются.

На самом базовом уровне электроны описываются квантовомеханическими моделями или их аппроксимациями – методом функционала плотности, динамической теорией среднего поля, моделью Хаббарда и т.д. Отсюда получаются эффективные спиновые модели, описывающие набор взаимодействующих спинов – такие, как модели Изинга и Гейзенберга. Наконец, на мезо- и макроскопическом уровне от набора спинов на решетке мы переходим к описанию намагниченности как плавно меняющегося в пространстве векторного поля, подчиняющегося уравнению Ландау-Лифшица-Гильберта. Численное решение такого уравнения называется микромагнитным моделированием: оно применяется, когда мы хотим посчитать пространственно неоднородную динамику намагниченности в образцах конечного размера (в том числе, например, перемещение доменных стенок).

Поведение магнитных материалов особенно интересно при наличии трех- или четырехспиновых взаимодействий, а также при наличии существенно анизотропных двухспиновых взаимодействий. Частным случаем последнего является взаимодействие Дзялошинского-Мория, способствующее образованию спиральных и закрученных спиновых текстур. При наличии такого взаимодействия в магнитных материалах могут образовываться устойчивые топологические возбуждения – скирмионы.

#магнетизм #объяснения

Вот как, на базовом уровне, возникает магнетизм.

Система сильно делокализованных (или «обобществленных») электронов с достаточно сильным кулоновским отталкиванием между собой склонна к ферромагнетизму. Действительно, как показано слева, при параллельной ориентации спинов принцип Паули запрещает электронам слишком сильно сближаться – это уменьшает энергию кулоновского отталкивания, а значит, выстраивание спинов параллельно энергетически выгодно.

Если же электроны перескакивают по сильно локализованным орбиталям, то возникает, наоборот, тенденция к антиферромагнетизму. Как показано в центре и справа, антипараллельная ориентация электронных спинов на соседних орбиталях позволяет им совершать виртуальные перескоки, «заходя в гости» друг к другу (что запрещено принципом Паули при параллельной ориентации). Это позволяет волновым функциям электронов распространяться по большей области пространства, понижая их кинетическую энергию – то есть, опять-таки, энергетически выгодно.

#магнетизм #объяснения #твердое_тело

В этой же статье дается хорошее объяснение того, в чем суть подхода DFT+U – метода функционала плотности, дополненного учетом отталкивания электронов на узле U, которое принципиально важно при описании сильно-коррелированных материалов.

В этом методе к энергии многоэлектронной системы добавляются два слагаемых. Первое из них повышает энергию системы на величину U, если два электрона занимают одну и ту же орбиталь (обычно здесь берутся кон-шемовские орбитали). Второе слагаемое – так называемый double counting term – вводится для того, чтобы скомпенсировать двойной учет одного и того же кулоновского взаимодействия. Потому что часть отталкивания на узле U уже содержится в исходном фукционале плотности – ее и нужно убрать.

На рисунке показаны зонная структура и плотность состояний FeO, считаемые в отсутствие (сверху) и при наличии (снизу) корреляционной добавки U. Как видно, при учете отталкивания на узле в спектре открывается щель и материал превращается в изолятор.

#объяснения #сильные_корреляции

А вот хорошая иллюстрация того, как работает взаимодействие Дзялошинского-Мория в магнетиках. К энергии системы оно добавляет слагаемое вида m∙[D∇×m], где m – вектор намагниченности, а матрица D может иметь разный вид, в зависимости от симметрии рассматриваемого материала или гетероструктуры.

На рисунке показаны три распространенных примера матриц D – диагональная, антидиагональная антисимметричная и антидиагональная симметричная. Взаимодействие Дзялошинского-Мория способствует стабилизации скирмионов – топологических возбуждений на фоне общего ферромагнитного выстраивания спинов. Разные структуры матриц D стабилизируют разные виды скирмионов.

Скирмионы не могут просто так «рассосаться» – это потребовало бы макроскопически больших затрат энергии на повороты огромного числа спинов против их ферромагнитного взаимодействия и взаимодействия Дзялошинского-Мория. Поэтому скирмионы могут лишь перемещаются по материалу под действием электрических и магнитных полей.

#магнетизм #объяснения

В этой работе рассмотрен графен в киральной электромагнитной полости – резонаторе, в котором электромагнитные моды правой и левой циркулярной поляризации взаимодействуют с электронами с разными силами или сдвинуты по частоте. При помощи преобразования Шриффера-Вольфа авторы исключили из гамильтониана системы электромагнитные моды и получили эффективный гамильтониан для электронов с модифицированной электронной дисперсией, в которой за счет полости открываются поляритонные щели.

Интересно, что можно рассмотреть не только случай пустой полости, но и полости в фоковском состоянии с определенным числом фотонов. В этом случае возникают топологические поляритоны – расщепления дисперсии с образованием топологически нетривиальных зон по обе стороны щели. А сами расщепленные дисперсии демонстрируют обмен фотонами: как показано на рисунке снизу, при движении вдоль дисперсии меняется среднее число фотонов в поляритонном состоянии, когда мы минуем точку антипересечения.

#фотоника #графен #топологические_материалы

Материал LK-99 нашумел несколько месяцев назад, когда в нем обнаружили сверхпроводимость и магнитную левитацию, существующие при комнатной температуре и исчезающие при температуре 400 К. В этом эксперименте попробовали воспроизвести синтез LK-99 и не обнаружили сверхпроводимости. Аномалии же сопротивления и магнитных свойств при 400 К, похожие на сверхпроводящий переход, оказались обусловлены структурным фазовым переходом в соединении Cu₂S, существующем в LK-99 в виде примеси.

Исследователи изготовили три образца LK-99: S1 и S2 по оригинальной методике и S3 по модифицированной схеме, исключающей подмешивание Cu₂S. Как видно на графиках сверху, S1 демонстрирует аномалии магнитной восприимчивости при 400 К, а S3 – нет. Электрическое сопротивление меняется скачком в S1 и S2 (графики в центре), причем в разную сторону, а S3 остается изолятором.

Графики снизу показывают, что похожие аномалии магнитных свойств и сопротивления наблюдаются в чистом Cu₂S, имеющемся в S1 и S2 в виде примеси.

#сверхпроводимость

Смешное: «хотя почти все эксперименты опровергли существование сверхпроводимости в LK-99, появилось множество теоретических работ, утверждающих, что сверхпроводимость в нем все-таки существует».

#сверхпроводимость #цитаты

Вот одна из ранних теоретических работ про спонтанное нарушение симметрии в PT-симметричной оптической системе при переходе через исключительную точку.

Авторы рассматривают плоский волновод, состоящий из областей с комплексно сопряженными показателями преломления n = n_w ± iαλ/4π. На графиках показано, как вещественная и мнимая часть эффективного показателя преломления N, с которым мода распространяется вдоль волновода, зависит от степени накачки в одном слое и утечки в другим α.

При α ниже критического значения имеются две моды с симметричным и антисимметричным профилями поля, как показано левой диаграммой снизу. Вдоль волновода эти моды не растут и не затухают (N вещественно), но распространяются с разными скоростями. При α выше критического значения PT-симметрия нарушается: как показано правой диаграммой снизу, одна мода смещается в область с потерями и становится затухающей, другая смещается в область с накачкой и растет по амплитуде при движении вдоль волновода.

#неэрмитовы_системы #электродинамика

Из статьи по PT-симметричной оптической системе:
«На первый взгляд, перебор всех возможных вариантов расчета мощности переданного сигнала, показанных на рисунке, неоправданно усложняет задачу. Но это не так – сами посмотрите, все становится очень просто и понятно...»

#неэрмитовы_системы #электродинамика #цитаты