Кадры из фильма «Дивергент» (2014 г.), на которых изображается повседневная жизнь фракции «эрудиция», отвечающей в тамошнем обществе за науку и знания. Нам показывают людей, которые носят пробирки, что-то обсуждают и смотрят в микроскопы – действительно, чем же еще в принципе могут заниматься ученые, кроме смотрения в микроскопы? Теоретиков ведь не существует. Сами ученые все, как на подбор, модельной внешности и одеты в элегантные деловые костюмы.

При этом – что странно! – они сидят, буквально упираясь друг в друга локтями, в скученном помещении, по которому бродят толпы народа. Выглядит это все как авральная работа какого-то медико-биологического десанта высокоразвитой цивилизации, который высадили вблизи очага эпидемии, поместили в наспех импровизированную лабораторию и заставили срочно брать анализы у зараженных и пытаться создать вакцину от зомби-вируса.

#цитаты #биология

Сканирующая туннельная спектроскопия позволяет определять плотность электронных состояний в материале при помощи измерения туннельного тока между образцом и иглой микроскопа. В простейшем случае дифференциальный туннельный ток dI/dV (производная тока I по напряжению смещения V между иглой и образцом) должен быть пропорционален плотности состояний. Однако иногда с этим возникает проблема: если электронам для попадания в образец нужно приобрести довольно большой импульс – например, попасть в долины K, Kʹ графена или дихалькогенидов переходных металлов – туннелирование сильно подавляется.

В случае двумерного MoSe₂ такая ситуация показана на рисунке зеленой кривой: в точках K_V и K_C мы должны уже натыкаться на потолок валентной зоны и дно зоны проводимости полупроводникового материала, где плотность состояний должна резко подниматься от нуля внутри щели до ненулевого значения. Но измеряемый дифференциальный туннельный ток dI/dV такого не демонстрирует.

#дихалькогениды_переходных_металлов #твердое_тело

В этой работе был придуман интересный метод, позволяющий справиться с проблемой подавления туннельного тока из-за несогласованности импульсов электрона в игле микроскопа и в образце при сканирующей туннельной спектроскопии (о которой шла речь в предыдущем посте).

Авторы проводили спектроскопию MoSe₂ с варьированием расстояния Z между иглой и образцом таким образом, чтобы туннельный ток I оставался постоянным. На рисунке синими кривыми показан дифференциальный туннельный ток dI/dV, посчитанный при постоянном I: как видно, он дает более честную картину пиков плотности состояний на границах энергетических зон, чем традиционное измерение при постоянном расстоянии Z, показанное зеленой кривой.

Величина κ = –½(∂ln I/∂Z), показанная черными кривыми, тоже дает интересную информацию. Это скорость экспоненциального спада туннельного тока с увеличением расстояния, пропорциональная [2mФ + (∆k)²]¹ᐟ², где Ф – высота туннельного барьера, ∆k – несогласованность импульсов электрона.

#дихалькогениды_переходных_металлов

А в этом эксперименте по сканирующей туннельной спектроскопии двумерного MoS₂ на поверхности графита наблюдалась красивая картина изгиба энергетических зон, типичная для полупроводниковых гетероструктур.

На панели (a) показаны картины плотности состояний, измеренные в разных точках траектории, изображенной на панели (b). Сначала мы находимся в толще MoS₂, где видна типичная полупроводниковая щель (кривые 01-19), но по мере приближения к краю образца она поднимается по энергии. На самом крае (кривая 21) мы видим, в соответствии с предсказаниями теории, металлические краевые состояния, частично заполняющие щель.

Если собрать информацию о положении краев валентной зоны и зоны проводимости MoS₂ как функций расстояния до края, мы увидим изгиб зон, показанный на панели (с) и простирающийся примерно на 5 нм. Он обусловлен пинингом уровня Ферми металлических краевых состояний к уровню Ферми окружающего графита и уровню Ферми толщи MoS₂.

#дихалькогениды_переходных_металлов #твердое_тело

С точки зрения теории информации, «разность между памятью и предсказательной способностью – это бесполезная ностальгия, то есть мера неэффективности модели».

#информация #цитаты

Интересная теоретическая работа, где выводится связь между эффективностью системы как термодинамической машины и ее же способностью к предсказаниям: оказывается, что одно немыслимо без другого!

Авторы рассматривают очень простую модель: система в дискретные моменты времени t принимает состояния s⁰, s¹, s² и так далее, причем делает это по некоторому вероятностному правилу p(sᵗ|sᵗ⁻¹, xᵗ). Как видно, новое состояние системы sᵗ зависит только от ее предыдущего состояния sᵗ⁻¹ (что подразумевает марковскую динамику) и от текущего состояния окружения xᵗ. Окружение тоже проходит через последовательность состояний x⁰, x¹, x², ..., но система на них никак не влияет (нет обратной связи) – они просто такие, какие есть, со своей заданной скоррелированной статистикой p(x⁰, x¹, x², …).

С термодинамической точки зрения, при каждом изменении состояния окружения xᵗ → xᵗ⁺¹ и текущем, фиксированном состоянии системы sᵗ окружение совершает над системой среднюю работу <Wᵗ>. С другой стороны, при обновлении состояния системы sᵗ⁻¹ → sᵗ по указанному выше вероятностному правилу и фиксированном состоянии окружения xᵗ она подвергается процессам внутренней релаксации с передачей тепла наружу. Помимо средней работы, можно ввести диссипировавшую работу <Wᵗ_diss> = <Wᵗ> – ∆Fᵗ_neq. Это важная величина, равная той части работы окружения над системой, которая не пошла на увеличение ∆Fᵗ_neq ее неравновесной свободной энергии (которую потом, в принципе, можно извлечь из системы обратно), а была потрачена впустую на диссипацию и затем превратилась в тепло. Иными словами, <Wᵗ_diss> служит мерой неэффективности системы как тепловой машины и термодинамической необратимости протекающих с ней процессов.

Чтобы связать термодинамические характеристики системы с ее предсказательной способностью, авторы две информационные величины. Первая из них Iᵗ_mem = I(sᵗ, xᵗ) – это мгновенная память, равная взаимной информации I(…) между текущим состоянием системы sᵗ и текущим состоянием окружения xᵗ. Это степень того, насколько сильно состояние системы оказывается прямым следствием состояния окружения, которое только что на нее повлияло. Вторая величина Iᵗ_pred = I(sᵗ, xᵗ⁺¹) – это мгновенная предсказательная способность, равная взаимной информации между текущим состоянием системы sᵗ и последующим состоянием окружения xᵗ⁺¹. Это мера того, насколько сильно наша система «готова» к непосредственному будущему.

При помощи несложных выкладок в работе выводится интересная формула, которая выглядит так:
< Wᵗ_diss >/T ≥ Iᵗ_mem – Iᵗ_pred,
где T – температура термостата, с которым взаимодействует система, отдавая ему тепло (и используемая, например, при расчете ∆Fᵗ_neq). Это неравенство говорит о том, что величина диссипировавшей работы не может быть меньше разности мгновенной памяти и мгновенной предсказательной способности.

Смысл его таков: чем хуже система предсказывает последующее состояние окружения (по сравнению с запоминанием его прошлых состояний), тем больше энергии она будет тратить впустую. Или, иными словами, любая система, обладающая памятью об окружающих событиях, должна учиться предсказывать будущее для того, чтобы иметь наибольшую термодинамическую эффективность и тратить меньше энергии на диссипацию.

#стохастическая_термодинамика #информация #отвал_башки

Динамическая теория среднего поля (dynamical mean-field theory, DMFT) – это метод, популярный для теоретического анализа сильно-коррелированных систем, где взаимодействия между частицами настолько сильны, что качественно меняют поведение системы и потому не могут учитываться по теории возмущений.

Согласно своему названию, DMFT учитывает динамические эффекты, но игнорирует эффекты пространственных корреляций (отсюда «среднее поле»). Иными словами, вместо функции Грина электронов G(k,ω), зависящей от импульса и частоты, мы рассматриваем локальную функцию Грина G_loc(ω), равную G(k,ω), просуммированной по импульсам k. Локальной эта функция G_loc(ω) называется потому, что она описывает запаздывающий (потому что он зависит от ω) отклик системы электронов в какой-нибудь точке r на помещение или удаление электрона в этой же точке r.

Записав, в каком-нибудь диаграммном приближении, уравнение Дайсона для G_loc(ω) и решив его, можно понять усредненные по импульсам свойства сильно-коррелированной системы. То есть DMFT позволяет учесть непертурбативным образом локальную часть сильных корреляций. Например, в рамках модели Хаббарда при половинном заполнении – канонической модели в физике сильно-коррелированных систем – этот метод прекрасно воспроизводит расщепление сплошной энергетической зоны на верхнюю и нижнюю зоны Хаббарда, разделенные существенно многочастичной щелью. А если взять нормальные и аномальные функции Грина, то можно решать и задачи сверхпроводимости в сильно-коррелированных материалах – таких, как высокотемпературные сверхпроводники на основе оксида меди.

В последние годы развиваются и нелокальные обобщения DMFT, где делается отход от локальности для учета пространственных корреляций. Например, локальной можно считать только двухчастичную функцию Грина, а одночастичную функцию Грина G(k,ω), считаемую диаграммно на основе двухчастичной, можно считать уже зависящей от импульса. В этой статье дается большой обзор нелокальных обобщений DMFT.

#сильные_корреляции #объяснения

Куча красивых диаграммок из обзора по нелокальным обобщения динамической теории среднего поля (DMFT).

#цитаты #сильные_корреляции

Принцип наименьшего действия – красивая штука, показывающая, как природа «выбирает» оптимальную траекторию движения из бесконечного множества возможных. Но на практике его используют лишь как математический инструмент для аналитического нахождения уравнений движения или самой траектории.

Авторы этой работы попытались применить принцип наименьшего действия, так сказать, по прямому назначению: для того, чтобы реально найти минимизирующую действие траекторию численно, методом градиентного спуска.

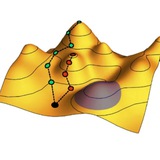
На рисунке показаны несколько примеров, рассмотренных авторами: свободное падение тела, колебания маятника и двойного маятника, гравитационная задача трех тел, движение 50 молекул, взаимодействующих посредством потенциала Ленарда-Джонса, и движение Земли по орбите вокруг Солнца.

На диаграммах показан процесс оптимизации траекторий, а на графиках черные, красные и синие кривые показывают, как в ходе оптимизации ведут себя действие S = ∫(T – V)dt и его кинетическая ∫Tdt и потенциальная –∫Vdt части.

#механика

Вот это крутая работа, в которой при помощи экспериментов на квантовом компьютере исследовалось возникновение так называемого измерительного фазового перехода (measurement-induced phase transition). Его можно понимать как переход между «квантовым» режимом, при котором наши измерительные приборы слишком слабы, чтобы дать достоверную информацию о состоянии системы, и «классическим» режимом, когда воздействие измерительных приборов на систему приводит к коллапсу ее волновой функции и получению точных результатов измерения, однозначно характеризующих состояние системы. Это совсем недавно появившаяся область исследований, ставшая возможной только благодаря появлению достаточно мощных квантовых компьютеров.

Если более конкретно, то измерительный фазовый переход возникает в следующей постановке задачи:
• У нас имеется квантовая система, которая подвергается поочередно то унитарной квантовой эволюции, то слабым измерениям. В ходе последовательности слабых измерений мы записываем историю их результатов M.
• Слабые измерения, при которых детектор лишь частично влияет на вектор состояния системы (а не резко проецирует его на собственные векторы оператора измеряемой величины, как при обычных проекционных измерениях), характеризуются параметром своей силы 0 ≤ γ ≤ 1.
• Оказывается, что при стремлении размера системы к бесконечности (в термодинамическом пределе) возникает резкое разграничение двух режимов: когда γ < γ_c, история результатов измерений M либо сильно флуктуирует, либо не дает никакой полезной информации о реальном состоянии системы. А при γ > γ_c история результатов М уже воспроизводима и дает достоверную информацию о состоянии системы.
• Как любой фазовый переход, в конечной системе измерительный переход размывается, то есть вместо резкого порога γ = γ_c мы получаем плавный переход, когда при увеличении γ информация M постепенно становится все более полезной.

В этой работе обнаружение измерительного фазового перехода рассматривается как задача познания: допустим, в каждом запуске эксперимента Ева получает последовательность результатов M, вставляет их в какую-нибудь модель (которая может обучаться на основе предшествующих успехов или ошибок) и пытается при помощи этой модели предсказать «настоящее» состояние системы, которое в самом конце ее эволюции определяется уже обычным, проекционным измерением. В зависимости от силы измерений γ возникают два режима: при γ < γ_c любая, даже самая гибкая и совершенная модель дает все худшие предсказания по мере того, как растет размер системы, и в термодинамическом пределе точность предсказаний падает до нуля. При γ > γ_c точность предсказаний модели, напротив, повышается с ростом размера системы (если модель достаточно гибкая и адекватна реальной динамике системы), а в термодинамическом пределе точность предсказаний стремится к 100%.

В качестве квантовой системы авторы взяли квантовый компьютер Quantinuum System Model H1, основанный на ионах в ловушках, а в качестве обучаемых моделей взяли три варианта: квантовую модель (симулирующую настоящую квантовую динамику, но затратную по вычислительным ресурсам), классическую статистическую модель (учитывающую вероятностный характер состояний, но упускающую квантовую когерентность) и нейронную сеть. Постепенно увеличивая число кубитов в системе до 14, им удалось наблюдать некие намеки на фазовый переход. Но для точного его наблюдения, конечно, нужны гораздо большие квантовые системы и большие вычислительные ресурсы для предсказывающей модели.

#квантовые_вычисления #квантовая_механика #отвал_башки

Вот картинка из статьи, показывающая схему и результаты эксперимента по наблюдению измерительного фазового перехода.

Как видно сверху, квантовая система – набор кубитов на ионах – подвергается действию двухкубитных гейтов (голубых блоков) и слабых измерений (оранжевых кружочков). В самом начале она приготавливается в суперпозиции двух «зарядов» Q = (1 + Z)/2, отличающихся на 1. Двухкубитные гейты генерируют хаотическую, но сохраняющую Q квантовую динамику, а последовательные измерения «склоняют» нашу систему к какому-то определенному значению Q (если они достаточно сильны), либо оставляют Q существенно неопределенным (если они слишком слабы), так что предсказать его значение становится очень сложно.

Как видно на графиках снизу, где-то в точке фазового перехода точность предсказаний С резко растет при увеличении силы измерений γ, а дисперсия этой точности демонстрирует пик. Увеличение числа кубитов L делает пик более острым, а его положение сходится к точке γ = 0.4.

#квантовые_вычисления #квантовая_механика

Еще любопытный факт из этой статьи: нейронную сеть (NN) можно, в принципе, достаточно легко – с обучающей выборкой, размер которой полиномиально растет с ростом размера системы L – обучить воспроизводить результаты классической статистической модели. А вот если пытаться обучить ее воспроизводить результаты модели квантовой динамики (PostBQP), то для этого требуются уже экспоненциально большие по L обучающие выборки.

В общем, чудес не бывает: нейронные сети, будучи универсальными аппроксиматорами, конечно же, могут уловить особенности квантовой динамики и потом их воспроизводить. Но для такого моделирования квантовой системы классической требуются экспоненциально большие вычислительные ресурсы.

#квантовые_вычисления #нейронные_сети

В недавнем эксперименте наблюдалось стимулированное усиление спиновых волн в ферромагнетике – эффект, который можно назвать магнонным аналогом лазера.

Тонкая полоска железо-иттриевого граната (YIG) показана на рисунке фиолетовым цветом. При помощи микроволн, подаваемых на полосковую линию слева, в ней возбуждаются магноны, которые распространяются вправо, проходя через центральную область. Именно она служит активной средой: на нее, через тонкий слой диэлектрика, подается резкий импульс напряжения, нагревающий пленку и создающий в ней неравновесное распределение магнонов с инверсией населенностей.

Измерение интенсивности магнонов, прошедших через активную область, производится справа при помощи бриллюэновского рассеяния света. Как показано на графике, после накачки импульсом напряжения поток магнонов оказывается в разы сильнее (синяя кривая), чем без нее (красная). Эффект усиления оказывается максимальным, когда магноны прибывают в активную область спустя 20-30 нс после импульса напряжения.

#магнетизм

Эксперименты показывают, что наше осязание гораздо более чувствительно, чем кажется на первый взгляд. Когда мы проводим пальцем по поверхности, мы ощущаем вибрации от фрикционного шума частотой до 1000 герц, делая по ним вывод о материале поверхности и ее структуре. Такие осязательные ощущения можно еще и усилить при помощи инструментов, обладающих высокой жесткостью и потому хорошо передающих вибрации: например, стоматологический зонд дает возможность врачу находить дефекты зубов на ощупь.

Передача вибраций важна и для создания протезов с хорошей тактильной обратной связью. Например, остеоперцепция – чувствительность костей к механическим вибрациям и нагрузкам – может использоваться для создания имитации осязания человеку с протезом руки. Для этого нужно, чтобы протез ввинчивался прямо в кость и передавал ей механические сигналы от кончиков пальцев в полосе частот до одного или нескольких килогерц – либо напрямую, через механический контакт, либо при помощи электроники.

#биология #популярное

В связи с тем, что для полноценного осязания нужно передавать вибрации частотой, как минимум, до 1000 герц, возникает вопрос создания подходящих для этой задачи материалов. Подобно тому, как материалы, прозрачные для света или для звука в нужной нам полосе частот, необходимы для обеспечения нам точного, неискаженного зрения или слуха, для осязания требуется создание легких и тонких материалов, «прозрачных» для механических вибраций.

Авторы этой работы смоделировали изготовили сэндвич-панели, состоящие из трехмерной полимерной структуры, напечатанной на 3D-принтере и помещенной между двумя слоями ткани из углеродного волокна. Такой выбор конструкции и материалов позволяет сделать структуру легкой и при этом жесткой как на растяжение/сжатие, так и на изгиб. Примеры измеренных спектров механического отклика, показанных на рисунке, демонстрируют, что на частотах до 1000 герц отклик остается почти постоянным – это значит, что структура должна «честно» передавать осязательные сигналы.

#механика #популярное

Помимо сэндвич-панелей, авторы этой работы попробовали сконструировать материалы для неискаженной передачи осязательных сигналов «с нуля», при помощи алгоритмической оптимизации. Алгоритмам, умеющим оптимизировать топологию и точную форму структуры, давалась задача максимально уменьшить ее массу, поддерживая при этом наименьшую из частот механических резонансов на уровне не ниже 1500 Гц.

На панелях A и B показан процесс оптимизации структуры, а на панели C видно, как при этом уменьшалась ее масса, а частота первого резонанса поддерживалась на уровне 1500 Гц. Оптимальная структура (панель D), напоминающая по виду уже что-то из живой природы, была изготовлена на 3D-принтере и исследована экспериментально. Спектр ее механического отклика, показанный на панели E, действительно удовлетворяет наложенным требованиям.

Кстати говоря, созданная компьютером структура оказалась на 19% легче и на 16% жестче, чем наилучшая по характеристикам сэндвич-панель, о которых шла речь в предыдущем посте.

#механика #популярное

Любопытная теоретическая работа, в которой рассчитано взаимодействие между возбуждениями вещества, обусловленное электромагнитными модами полости.

Как показано на рисунке, авторы рассматривают возбуждения вещества, взаимодействующие с электрическим полем полости своими дипольными моментами μ. Если считать, что частоты всех мод полости (начинающиеся с какой-то минимальной) много больше энергий возбуждения вещества, то моды полости можно исключить из задачи, получив для вещества эффективный гамильтониан, в котором дипольные моменты μ взаимодействуют уже непосредственно друг с другом. Самое интересное, что величина взаимодействия λ между диполями дается функцией Грина G электромагнитного поля в полости, посчитанной в статическом пределе ω = 0.

Таким образом, учет всех высокочастотных мод, переносящих взаимодействие между диполями, сводится к их электростатическому взаимодействию – результат, кажущийся очевидным, но доказанный точно на основе спектральных свойств функции Грина.

#электродинамика #фотоника

Чистая вода почти прозрачна для света в видимом диапазоне, поэтому нагревание воды при ее освещении, приводящее к испарению – довольно слабо идущий процесс. Однако есть множество указаний на то, что в реальности испарение воды идет сильнее, чем можно было бы ожидать на основе поглощения света.

В этой работе при помощи 13 (!) экспериментов было доказано, что такой эффект действительно существует. Оказывается, при облучении воды светом вблизи ее поверхности образуется градиент электрического поля, который, действуя на квадрупольный момент молекул, вырывает с поверхности целые кластеры воды. Энергии одного фотона как раз хватает для разрыва множества водородных связей. В зависимости от условий, эти кластеры потом могут окончательно испариться, а могут попадать в воду обратно.

Интересно, что такой фотомолекулярный эффект возникает только при облучении воды светом TM-поляризации, потому что у него имеется компонента поля, направленная перпендикулярно поверхности.

#химия #электродинамика #отвал_башки

Авторы статьи про фотомолекулярный эффект предполагают, что открытый ими эффект может объяснить часто наблюдаемое явление, когда «солнце развеивает туман».

Действительно, капельки воды, будучи почти прозрачными, сами по себе слишком слабо поглощают свет, чтобы заметно нагреваться и испаряться в солнечных лучах. Другое дело – фотомолекулярный эффект, при котором электрическое поле световой волны вырывает кластеры молекул воды с ее поверхности. У мелких капелек тумана отношение площади поверхности к объему очень велико, поэтому поверхностные эффекты должны идти весьма интенсивно.

#электродинамика #химия #цитаты

Исключительная точка неэрмитовой системы – это точка пространства параметров, в которой происходит бифуркация собственных значений гамильтониана, а поведение системы качественно меняется. В качестве неэрмитовой можно описывать систему, взаимодействующую с термостатом и передающую ему энергию в форме релаксации.

Но ведь совокупность системы и термостата описывается эрмитовым гамильтонианом – как здесь возникает исключительная точка, когда размер термостата стремится к бесконечности? В этой статье демонстрируется процесс эффективной «потери эрмитовости» на языке величины D₁₂(T) – это дисперсия отношения амплитуд колебаний двух осцилляторов, из которых состоит система, считаемая в среднем по начальным условиям и достаточно большому времени T.

На графиках видно, как она ведет себя похожим образом при пересечении исключительной точки в неэрмитовой (слева) и в эрмитовой (справа) системах. Получается, эта величина действительно улавливает нечто общее для открытой и замкнутой квантовых систем.

#неэрмитовы_системы

Ну вот, теперь постмодернизм добрался и до термодинамики... 😐

#термодинамика #цитаты