Пишу о статьях по физике и другим темам, которые показались мне интересными.

Список тегов:
#популярное 👀
#объяснения 🧑🏻‍🏫
#отвал_башки 🤯

#акустика
#астрофизика
#атомные_газы
#биология
#бозе_конденсация
#геометрия
#геофизика
#гидродинамика
#графен
#дихалькогениды_переходных_металлов
#информация
#квантовая_механика
#квантовая_термодинамика
#квантовые_вычисления
#магнетизм
#математика
#механика
#Монте_Карло
#мягкая_материя
#наноструктуры
#нейронные_сети
#неэрмитовы_системы
#общество
#оптимизация
#открытые_квантовые_системы
#плазмоны
#поляритоны
#самоорганизация
#сверхпроводимость
#сверхтекучесть
#сильные_корреляции
#состояния_Флоке
#стекла
#стохастическая_термодинамика
#суперсолид
#твердое_тело
#термодинамика
#топологические_материалы
#уровни_Ландау
#фазовые_переходы
#фононы
#фотоника
#фракталы
#хаос
#химия
#цитаты
#экситоны
#электродинамика
#электроника
#элементарные_частицы
#ядерная_физика

Познавательная статья, дающая педагогическое введение в тему квантового броуновского движения. Это движение частицы, взаимодействующей с термостатом – как правило, набором большого числа независимых гармонических осцилляторов.

Сначала авторы подробно описывают классическое броуновское движение, показывая, как из связанных уравнений динамики самой частицы и частиц термостата можно исключить термостат, получив – при некоторых допущениях – уравнение Ланжевена. Роль термостата сводится к воздействию на частицу двух сил: силы трения и случайной силы, отвечающей за тепловое движение. Важный момент здесь – флуктуационно-диссипационная теорема, связывающая между собой величину трения, интенсивность случайной силы и температуру термостата.

Затем описывается уже квантовое броуновское движение. Здесь все похоже, только воздействие термостата выражается уже операторами. А еще из-за бозе-статистики осцилляторов термостата во многих выражениях, характеризующих его воздействие на частоте ω, появляются множители вида cth(ω/2T). Авторы отдельно обсуждают квантовую теорему о равнораспределении энергии по степеням свободы, которая, из-за комбинации квантовых эффектов и диссипации, имеет не совсем тривиальный вид.

Еще одна любопытная штука – диссипативный диамагнетизм, возникающий при двумерном квантовом броуновском движении в магнитном поле. Взаимодействие заряженной частицы с термостатом приводит к дополнительному вкладу в ее магнитный отклик. Полезно и то, что в статье проводятся связи между квантовым броуновским движением и современными темами, такими как стохастическая термодинамика и флуктуационные теоремы.

#объяснения #открытые_квантовые_системы

Красивая экспериментальная работа, в которой был реализован топологический изолятор Андерсона – материал, который становится топологически нетривиальным лишь под влиянием достаточно сильного беспорядка. Это одна из первых реализаций материалов такого класса.

https://telegra.ph/Topologicheskij-izolyator-Andersona-dlya-fotonov-07-03

#топологические_материалы #фотоника

Работа из разряда «техника на грани фантастики»: автономная лаборатория «Ада», которая самостоятельно занимается поиском оптимальных технологических процессов синтеза материалов. Лаборатория состоит из компьютерной системы и роботизированной платформы, способной подбирать реагенты, изготавливать образцы материала и исследовать их свойства. На один образец у нее уходит 20-30 минут, нужно только поставлять ей расходники.

В предыдущей работе эта лаборатория училась создавать тонкие пленки органического полупроводника с дырочной проводимостью. Ее целью было добиться наибольшей подвижности дырок при варьировании степени допирования материала и времени его отжига. Меньше чем за сутки она полностью без вмешательства человека нашла оптимальные условия, повысив исходную подвижность дырок на 1-2 порядка.

Здесь «Ада» подбирала условия изготовления тонких проводящих пленок палладия на полимерной подложке. Ее целью было определить парето-фронт: кривую в пространстве свойств материала – в данном случае проводимости пленки и температуры отжига, – показывающую достижимый на практике компромисс между ними (чем больше нужна проводимость пленки, тем более высокой должна быть температура).

Ей удалось найти не только оптимальные технологии процессов для уже известных раньше пленок, изготавливаемых при температуре 250 °C, но и открыть новые методы, требующие более низкой температуры 190 °C и расширяющие диапазон полимеров, которые можно использовать в качестве подложки.

Особая ценность таких автономных лабораторий в том, что они могут довольно быстро и эффективно проводить поиск в многомерном пространстве параметров, характеризующих технологический процесс (концентрации легирующих примесей, температуры и длительности отжига, времена напыления и т.д.). Человеку же довольно тяжело ориентироваться в пространствах таких размерностей, удерживая в голове множество факторов одновременно.

Результат получается почти как в компьютерной игре, когда ты нажимаешь исследовать апгрейд брони своих юнитов, и через некоторое время получаешь технологию «броня +1» без необходимости самому заниматься материаловедением и лабораторными экспериментами.

#популярное #отвал_башки

Достаточно очевидно, что турбулентность, со своей фрактальной структурой потоков и завихрений, должна демонстрировать масштабную инвариантность, то есть выглядеть одинаково при равномерном растяжении или сжатии системы. Конформная же инвариантность – это более сильное свойство, состоящее в неизменности статистических свойств при неравномерных растяжениях или сжатиях, сохраняющих углы. Такое свойство двумерной турбулентности было проверено в экспериментах.

https://telegra.ph/Poznavatelnaya-statya-dayushchaya-pedagogicheskoe-vvedenie-v-temu-kvantovogo-brounovskogo-dvizheniya-EHto-dvizhenie-chasticy-vza-07-03

#гидродинамика #фракталы

А вот недавняя работа, тоже посвященная конформной инвариантности двумерного турбулентного движения, но не обычного, а сверхтекучего. Здесь был проведен эксперимент с бозе-конденсатом экситонных поляритонов.

Особенность сверхтекучей турбулентности в том, что она завязана на дискретные единицы – квантованные вихри, из-за чего ее масштабная инвариантность слегка нарушается. Тем не менее, на масштабах длины залечивания конденсата картина завихренности, показанная слева, демонстрирует все свойства, характерные для конформной инвариантности – в том числе, степенное распределение размеров с показателем 96/91. Графики же справа демонстрируют масштабную инвариантность на больших расстояниях: статистическое распределение циркуляций скорости, посчитанных вдоль квадратных петель различных размеров R (превышающих длину залечивания 2.3 мкм), ложится на одну и ту же кривую. Причем кривая эта степенная, а не гауссова – что тоже свидетельствует об отсутствии характерного масштаба.

#гидродинамика #сверхтекучесть #поляритоны

Полезная диаграмма из небольшого обзора по сверхбыстрой динамике электронов, дырок и экситонов в гетероструктурах двумерных дихалькогенидов переходных металлов. На этой диаграмме для каждого материала показано расположение валентной зоны и зоны проводимости, найденное при помощи функционала плотности PBE (синие полоски) и метода GoWo (розовые полоски). Поскольку функционал плотности часто ошибается насчет щели в полупроводниках, розовые полоски дают более надежные результаты.

Из этой диаграммы видно, что при контакте практически любой пары материалов возникает выравнивание зон II-го типа: когда в общую энергетическую щель частично залазит валентная зона одного материала и зона проводимости другого материала. В таком случае низшим по энергии возбуждением будет межслойный экситон.

#дихалькогениды_переходных_металлов #экситоны

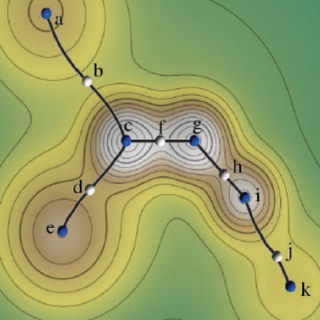
Любопытная работа, в которой не только описывается простая модель биологического видообразования, но и проводятся интересные физические параллели: разделение популяции на отдельные виды во многом похоже на нарушение симметрии реплик в спиновом стекле – застревании системы в одном из бассейнов эргодичности.

https://telegra.ph/Vidoobrazovanie-v-modeli-spinovogo-stekla-07-04

#стекла #биология #фазовые_переходы #популярное

Вот это очень крутая работа фундаментального уровня, устанавливающая взаимосвязь между краевыми модами топологического изолятора и квантовыми состояниями неэрмитовой системы.

Давно было замечено, что магнитные краевые каналы, распространяющиеся лишь в одну сторону вдоль границы двумерной системы (электронного газа в магнитном поле либо модели Холдейна), очень похожи на состояния частиц в неэрмитовой модели Хатано-Нельсона. Это одномерная цепочка с перескоками между соседними узлами, имеющими разные амплитуды в направлениях влево и вправо. Из-за такой асимметрии состояния, движущиеся в одном направлении, экспоненциально усиливаются, а в другом направлении – наоборот, затухают. Если мы рассмотрим динамику на больших временах, когда выживают лишь состояния, движущиеся «по течению», эффективно получается аналог однонаправленной краевой моды.

Авторы этой работы показывают, что такая параллель – не просто случайное совпадение. Краевая мода любого эрмитового (d+1)-мерного топологического изолятора, эквивалентна – в смысле динамики на больших временах – некоторой d-мерной системе с неэрмитовым гамильтонианом. При этом класс симметрии топологического изолятора (один из 10 классов Алтланда-Цирнбауэра) однозначно связан с классом симметрии неэрмитовой системы (одним из 38 классов Бернарда-ЛеКлера). А необычные свойства краевых мод – такие, как невзаимность, безмассовость или киральность – естественным образом воспроизводятся и неэрмитовой моделью, имеющей на единицу меньшую размерность.

#объяснения #топологические_материалы #неэрмитовы_системы

Загадочные каббалистические диаграммы из статьи из предыдущего поста.

То, что чаще всего называют соотношением неопределенностей Гейзенберга, на самом деле является либо соотношением неопределенностей Кеннарда-Вейля, либо соотношением неопределенностей Робертсона-Шредингера. Сам же Гейзенберг сформулировал лишь качественный принцип неопределенности.

Вот табличка, помогающая не запутаться во всех этих неопределенностях.

#объяснения #квантовая_механика