«Смотрите, стайка голубьёв!» Эти видео демонстрируют, как определялись иерархии в стае голубей. На первом видео – видеозапись приема пищи, на которой положение каждого голубя отслеживает по прикрепленному к нему флагу цветному идентификатору. Доминирование определяется по тому, как один голубь блокирует доступ другого к кормушке.
Второе видео демонстрирует иерархию, проявляющуюся в избегании столкновений: доминирующий голубь движется на подчиненного, а тот пытается избежать сближения. Это можно определить автоматически по взаимным координатам голубей и векторам их скоростей. Доминирование же, проявляющееся в том, кто кого клюет и кто на кого нападает, люди определяли вручную, путем просмотра примерно половины видеозаписей.
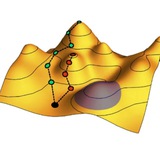
На третьем видео показано, как определяется иерархия лидерства при стайном полете: если один голубь меняет направление полета первым, а другой делает это чуть позже, то первый считается лидером по сравнению со вторым.
#биология #популярное #общество
Второе видео демонстрирует иерархию, проявляющуюся в избегании столкновений: доминирующий голубь движется на подчиненного, а тот пытается избежать сближения. Это можно определить автоматически по взаимным координатам голубей и векторам их скоростей. Доминирование же, проявляющееся в том, кто кого клюет и кто на кого нападает, люди определяли вручную, путем просмотра примерно половины видеозаписей.
На третьем видео показано, как определяется иерархия лидерства при стайном полете: если один голубь меняет направление полета первым, а другой делает это чуть позже, то первый считается лидером по сравнению со вторым.
#биология #популярное #общество
Еще несколько фактов насчет иерархий в стае голубей:
• Блокирование приема пищи демонстрирует довольно сильную степень взаимности: если голубь A систематически блокирует доступ голубя B к кормушке (и, таким образом является доминирующим), то голубь B тоже довольно часто (хотя и в меньшем числе случаев) будет блокировать доступ голубю A.
• Все изученные иерархические отношения – приема пищи, избегания сближений, драк и клевания, лидерства в полете – у голубей оказались транзитивными. Это значит, что если голубь A доминирует (или лидирует) над голубем B, а голубь B доминирует над голубем C, то A доминирует над C. Иными словами, иерархические отношения не имеют замкнутых циклов вида A → B → C → A, при которых угнетение могло бы идти по кругу.
• То, что иерархии силового доминирования и лидерства в полете у голубей независимы – нетривиальный факт. Например, у волков и павианов эти две иерархии почти совпадают: самые сильные доминирующие особи являются одновременно и лидерами при стайном перемещении. Вероятно, особенность голубей здесь в том, что в полете невозможно устраивать драки и прочие взаимодействия, на которых строится силовое доминирование, поэтому на первый план выступают другие компетенции – знание местности, способность ориентироваться и хорошая память.
#биология #популярное #общество
• Блокирование приема пищи демонстрирует довольно сильную степень взаимности: если голубь A систематически блокирует доступ голубя B к кормушке (и, таким образом является доминирующим), то голубь B тоже довольно часто (хотя и в меньшем числе случаев) будет блокировать доступ голубю A.
• Все изученные иерархические отношения – приема пищи, избегания сближений, драк и клевания, лидерства в полете – у голубей оказались транзитивными. Это значит, что если голубь A доминирует (или лидирует) над голубем B, а голубь B доминирует над голубем C, то A доминирует над C. Иными словами, иерархические отношения не имеют замкнутых циклов вида A → B → C → A, при которых угнетение могло бы идти по кругу.
• То, что иерархии силового доминирования и лидерства в полете у голубей независимы – нетривиальный факт. Например, у волков и павианов эти две иерархии почти совпадают: самые сильные доминирующие особи являются одновременно и лидерами при стайном перемещении. Вероятно, особенность голубей здесь в том, что в полете невозможно устраивать драки и прочие взаимодействия, на которых строится силовое доминирование, поэтому на первый план выступают другие компетенции – знание местности, способность ориентироваться и хорошая память.
#биология #популярное #общество
PNAS
Context-dependent hierarchies in pigeons | PNAS
Hierarchical organization is widespread in the societies of humans and other animals,
both in social structure and in decision-making contexts. In ...
both in social structure and in decision-making contexts. In ...
Вот одно из проявлений универсальности фазовых переходов. Как мы знаем, плотность жидкости и плотность полученного из нее пара сильно различаются, даже когда они находятся во взаимном равновесии, при одной и той же температуре.
Однако, когда температура превышает критическую (для воды, к примеру, это около 374 °C), различие между жидкостью и газом пропадает. Если нарисовать плотности ρ жидкости и пара как функции температуры T, причем плотности взять в единицах плотности ρ_c в критической точке, а температуру – в единицах критической температуры T_c, то все зависимости для разных жидкостей укладываются на одну и ту же кривую.
Причина такой универсальности – независимости от химического состава, деталей свойств и взаимодействий молекул жидкостей – в том, что в точке фазового перехода между жидкостью и газом ключевую роль играет предельно крупномасштабное поведение системы, а не ее микроскопические детали.
#термодинамика #популярное #объяснения
Однако, когда температура превышает критическую (для воды, к примеру, это около 374 °C), различие между жидкостью и газом пропадает. Если нарисовать плотности ρ жидкости и пара как функции температуры T, причем плотности взять в единицах плотности ρ_c в критической точке, а температуру – в единицах критической температуры T_c, то все зависимости для разных жидкостей укладываются на одну и ту же кривую.
Причина такой универсальности – независимости от химического состава, деталей свойств и взаимодействий молекул жидкостей – в том, что в точке фазового перехода между жидкостью и газом ключевую роль играет предельно крупномасштабное поведение системы, а не ее микроскопические детали.
#термодинамика #популярное #объяснения
👍2
Любопытное теоретическое исследование активной материи в виде множества вытянутых стержней, самостоятельно движущихся вдоль своей оси и помещенных на поверхность сферы.
Сверху на рисунке представлена фазовая диаграмма системы в переменных плотности стержней (по горизонтали) и их пропорций – отношения длины к ширине (по вертикали). Структура фаз проиллюстрирована снизу. Помимо обычных газа и жидкости, существует фаза изолированных скоплений, специфичная именно для активных частиц: двигаясь вдоль своей оси, стержни сталкиваются и застревают, образуя скопления. При большей плотности сгустки соединяются в единый кристалл-нематик, но в нем неизбежно присутствуют дефекты: из за «теоремы о причесывании ежа» на сфере невозможно создать выровненную структуру без топологических дефектов.
Стекло – тоже интересная фаза в случае активной материи. Хотя стержни запутываются в полностью аморфную структуру, из-за комбинация движущих сил заставляет ее вращаться как единое целое вокруг оси сферы.
#самоорганизация #стекла
Сверху на рисунке представлена фазовая диаграмма системы в переменных плотности стержней (по горизонтали) и их пропорций – отношения длины к ширине (по вертикали). Структура фаз проиллюстрирована снизу. Помимо обычных газа и жидкости, существует фаза изолированных скоплений, специфичная именно для активных частиц: двигаясь вдоль своей оси, стержни сталкиваются и застревают, образуя скопления. При большей плотности сгустки соединяются в единый кристалл-нематик, но в нем неизбежно присутствуют дефекты: из за «теоремы о причесывании ежа» на сфере невозможно создать выровненную структуру без топологических дефектов.
Стекло – тоже интересная фаза в случае активной материи. Хотя стержни запутываются в полностью аморфную структуру, из-за комбинация движущих сил заставляет ее вращаться как единое целое вокруг оси сферы.
#самоорганизация #стекла
👍3
А вот, для сравнения, что происходит в случае таких же активных частиц в форме вытянутых стержней, но помещенных на плоскую поверхность. Главное отличие от системы, описанной в предыдущем посте – это существование выстроенной фазы, называемой здесь словом “laning”.
Это фаза, в которой стержни выстроены в параллельные ряды, причем разные ряды движутся в случайных направлениях – похоже на многополосную автомобильную дорогу, отсюда и название. На сфере, в отличие от плоской поверхности, такая фаза невозможна из-за «теоремы о причесывании ежа».
#самоорганизация #стекла
Это фаза, в которой стержни выстроены в параллельные ряды, причем разные ряды движутся в случайных направлениях – похоже на многополосную автомобильную дорогу, отсюда и название. На сфере, в отличие от плоской поверхности, такая фаза невозможна из-за «теоремы о причесывании ежа».
#самоорганизация #стекла
👍1
Полезная статья о том, как квантовые геометрические эффекты влияют на функции отклика сверхпроводников. Как я писал раньше, сильнее всего квантовая геометрия проявляется в случае плоских энергетических зон, когда геометрические вклады, например, в сверхтекучую плотность – единственное, что остается отличным от нуля. В общем случае нужно рассматривать как традиционные вклады, обусловленные дисперсией, так и геометрические вклады, обусловленные структурой волновых функций.
Авторы проводят расчеты, отталкиваясь от среднеполевого гамильтониана сверхпроводника, содержащего спаривающий потенциал – члены, пропорциональные cc и c⁺c⁺. Нетривиальная геометрия электронных состояний меняет и структуру такого потенциала, что отражается на последующих расчетах термодинамического потенциала и функций отклика.
На рисунке показан простой пример формул для термодинамического потенциала сверхпроводника Ω, состоящего из обычных пара- и диамагнитных вкладов, и дополнительного геометрического вклада.
#сверхпроводимость
Авторы проводят расчеты, отталкиваясь от среднеполевого гамильтониана сверхпроводника, содержащего спаривающий потенциал – члены, пропорциональные cc и c⁺c⁺. Нетривиальная геометрия электронных состояний меняет и структуру такого потенциала, что отражается на последующих расчетах термодинамического потенциала и функций отклика.
На рисунке показан простой пример формул для термодинамического потенциала сверхпроводника Ω, состоящего из обычных пара- и диамагнитных вкладов, и дополнительного геометрического вклада.
#сверхпроводимость
👍4
Сингулярности Ван Хова – это особенности (изломы, разрывы и интегрируемые сингулярности) зависимости плотности состояний от энергии, возникающие в кристалле из-за критических точек, то есть точек в пространстве квазиимпульса, где первая производная электронной дисперсии обращается в ноль. В зависимости от поведения матрицы вторых производных, в них имеются максимумы, минимумы или седловые точки дисперсии.
Но бывают сингулярности Ван Хова высшего порядка, где обращаются в ноль не только первые, но и вторые производные. К примеру, в двумерном материале седловая точка (обычная сингулярность Ван Хова) дает логарифмический пик в плотности состояний ρ(E) ~ ln|E – Eₒ|, а сингулярность Ван Хова высшего порядка дает более сильный, степенной пик ρ(E) ~ |E – Eₒ|⁻¹ᐟ⁴.
В этой работе показано, что зонная структура электронов на поверхности Sr₂RuO₄, подвергающейся кристаллической реконструкции, довольно близка к появлению сингулярности Ван Хова высшего порядка на уровне Ферми.
#твердое_тело
Но бывают сингулярности Ван Хова высшего порядка, где обращаются в ноль не только первые, но и вторые производные. К примеру, в двумерном материале седловая точка (обычная сингулярность Ван Хова) дает логарифмический пик в плотности состояний ρ(E) ~ ln|E – Eₒ|, а сингулярность Ван Хова высшего порядка дает более сильный, степенной пик ρ(E) ~ |E – Eₒ|⁻¹ᐟ⁴.
В этой работе показано, что зонная структура электронов на поверхности Sr₂RuO₄, подвергающейся кристаллической реконструкции, довольно близка к появлению сингулярности Ван Хова высшего порядка на уровне Ферми.
#твердое_тело
Хорошая иллюстрация того, что происходит с химическим потенциалом и концентрацией электронов в допированном полупроводнике при разных температурах .
Химический потенциал μ определяется подгонкой суммарного числа электронов под распределение Ферми-Дирака 1/{exp[(E – μ)/T] + 1}, умноженное на плотность состояний и проинтегрированное по энергии. При низких температурах T → 0 химический потенциал превращается в уровень Ферми μ = E_F, и в случае полупроводника n-типа он располагается между заполненными энергетическими уровнями донорных примесей E_D и краем незаполненной зоны проводимости E_C.
При промежуточных температурах E_C – E_D << T < E_g примеси ионизуются, за счет чего в зоне проводимости образуется почти постоянная концентрация электронов n. При высоких температурах T >> E_g, превышающих щель, химический потенциал располагается уже внутри основной щели (как в недопированном полупроводнике), а концентрация электронов n растет благодаря их тепловой активации из валентной зоны.
#твердое_тело #объяснения
Химический потенциал μ определяется подгонкой суммарного числа электронов под распределение Ферми-Дирака 1/{exp[(E – μ)/T] + 1}, умноженное на плотность состояний и проинтегрированное по энергии. При низких температурах T → 0 химический потенциал превращается в уровень Ферми μ = E_F, и в случае полупроводника n-типа он располагается между заполненными энергетическими уровнями донорных примесей E_D и краем незаполненной зоны проводимости E_C.
При промежуточных температурах E_C – E_D << T < E_g примеси ионизуются, за счет чего в зоне проводимости образуется почти постоянная концентрация электронов n. При высоких температурах T >> E_g, превышающих щель, химический потенциал располагается уже внутри основной щели (как в недопированном полупроводнике), а концентрация электронов n растет благодаря их тепловой активации из валентной зоны.
#твердое_тело #объяснения
В этой работе предложен интересный способ измерения невзаимного электромагнитного отклика материалов и наноструктур. Авторы предлагают помещать исследуемый образец на перекрестье двух электромагнитных резонаторов, так что недиагональные компоненты его диэлектрической восприимчивости χ_xy и проводимости σ_xy связывают фотонные моды в этих резонаторах между собой.
От операторов фотонов a и b в двух резонаторах при помощи преобразования Швингера можно перейти к эффективным операторам спина S_x = ½(a⁺b + b⁺a), S_x = ½(ia⁺b – ib⁺a), S_z = ½(a⁺a – b⁺b), длина которого сохраняется при сохранении полного числа фотонов a⁺a + b⁺b. Такой спин, в ходе своей эволюции с течением времени, подвергается действию эффективного магнитного поля с компонентами {χ_xy, σ_xy, Δω}, где Δω – расстройка частот резонаторов. Поэтому, приготавливая заданные квантовые состояния фотонов в двух резонаторах и регистрируя их эволюцию за определенный промежуток времени, можно проводить очень точные измерения χ_xy и σ_xy.
#фотоника
От операторов фотонов a и b в двух резонаторах при помощи преобразования Швингера можно перейти к эффективным операторам спина S_x = ½(a⁺b + b⁺a), S_x = ½(ia⁺b – ib⁺a), S_z = ½(a⁺a – b⁺b), длина которого сохраняется при сохранении полного числа фотонов a⁺a + b⁺b. Такой спин, в ходе своей эволюции с течением времени, подвергается действию эффективного магнитного поля с компонентами {χ_xy, σ_xy, Δω}, где Δω – расстройка частот резонаторов. Поэтому, приготавливая заданные квантовые состояния фотонов в двух резонаторах и регистрируя их эволюцию за определенный промежуток времени, можно проводить очень точные измерения χ_xy и σ_xy.
#фотоника
👍2
Для того, чтобы методом обратной диффузии генерировать изображения, принадлежащие к определенному классу, можно использовать направление при помощи классификатора или направление без классификатора – второй способ сейчас является общепринятым.
Но как генерировать изображения, не принадлежащие к одному из нескольких жестко разделенных классов, а по текстовому описанию свободного формата? Общий принцип здесь примерно такой же, как при направлении обратной диффузии без использования классификатора: в ходе обучения нейросети мы подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она могла воспроизводить случайный гауссов шум при любых значениях аргументов – текущего изображения x, метки его класса y и номера шага диффузии t. Только вместо дискретных меток класса y можно использовать любой результат «переваривания» текстовых фраз языковой моделью – отдельной нейросетью, превращающей текстовую фразу z в высокоуровневую информацию y о ее содержании, называемую вложением (embedding).
Таким образом, процесс обучения нейросети, генерирующей изображения по текстовому описанию, выглядит, в общих чертах, следующим образом:
• Берем предварительно обученную языковую модель-кодировщик, умеющую превращать любую текстовую строку z в ее переработанное вложение y.
• Берем нейросеть, позволяющую достаточно гибко подгонять функцию ϵ_θ(x, y, t) трех аргументов – x (изображения), y (вложения текстовой фразы) и t (номера шага диффузии).
• Добываем библиотеку обучающих примеров – пар изображений xᵢ⁽⁰⁾ и прилагающихся к ним текстовых описаний zᵢ.
• Используя эту библиотеку, подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она минимизировала ошибку ||ϵ_θ(x, y, t) – ϵ||² – отклонение от случайного гауссового шума ϵ, при этом аргументы x и y строятся на элементах обучающей выборки: x является линейной комбинацией xᵢ⁽⁰⁾ и ϵ с коэффициентами, зависящими от t, а y вычисляется языковой моделью на основе zᵢ.
• После того, как функция ϵ_θ(x, y, t) обучена, нейросеть готова к работе: по любому новому текстовому описанию z языковая модель генерирует его вложение y, а затем с этим аргументом функция ϵ_θ(x, y, t) используется для «отмены» шума на каждом шаге обратной диффузии.
Нейросеть
#нейронные_сети #популярное
Но как генерировать изображения, не принадлежащие к одному из нескольких жестко разделенных классов, а по текстовому описанию свободного формата? Общий принцип здесь примерно такой же, как при направлении обратной диффузии без использования классификатора: в ходе обучения нейросети мы подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она могла воспроизводить случайный гауссов шум при любых значениях аргументов – текущего изображения x, метки его класса y и номера шага диффузии t. Только вместо дискретных меток класса y можно использовать любой результат «переваривания» текстовых фраз языковой моделью – отдельной нейросетью, превращающей текстовую фразу z в высокоуровневую информацию y о ее содержании, называемую вложением (embedding).
Таким образом, процесс обучения нейросети, генерирующей изображения по текстовому описанию, выглядит, в общих чертах, следующим образом:
• Берем предварительно обученную языковую модель-кодировщик, умеющую превращать любую текстовую строку z в ее переработанное вложение y.
• Берем нейросеть, позволяющую достаточно гибко подгонять функцию ϵ_θ(x, y, t) трех аргументов – x (изображения), y (вложения текстовой фразы) и t (номера шага диффузии).
• Добываем библиотеку обучающих примеров – пар изображений xᵢ⁽⁰⁾ и прилагающихся к ним текстовых описаний zᵢ.
• Используя эту библиотеку, подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она минимизировала ошибку ||ϵ_θ(x, y, t) – ϵ||² – отклонение от случайного гауссового шума ϵ, при этом аргументы x и y строятся на элементах обучающей выборки: x является линейной комбинацией xᵢ⁽⁰⁾ и ϵ с коэффициентами, зависящими от t, а y вычисляется языковой моделью на основе zᵢ.
• После того, как функция ϵ_θ(x, y, t) обучена, нейросеть готова к работе: по любому новому текстовому описанию z языковая модель генерирует его вложение y, а затем с этим аргументом функция ϵ_θ(x, y, t) используется для «отмены» шума на каждом шаге обратной диффузии.
Нейросеть
Imagen от корпорации Google использует такой метод генерации изображения на основе текстовой модели T5. Другая нейросеть – ее конкурент GLIDE от компании OpenAI – используeт вместо этого CLIP-вложения. А именно, в качестве аргумента y используется не просто результат переработки текстовой строки, а ее перекрытие с результатом переработки текущего изображения x. Похожим образом работает нейросеть unCLIP, также от компании OpenAI. Нейросеть eDiff-I от корпорации Nvidia для направления обратной диффузии применяет комбинацию текстовой модели T5 и CLIP-вложений: первая в большей степени используется на ранних этапах генерации, вторая – с большим весом на поздних этапах.#нейронные_сети #популярное
Telegram
Бассейн эргодичности
Некоторые популярные нейросети, занимающиеся генерацией изображений, такие как Midjorney, DALL-E и Stable Diffusion, работают по принципу обратной диффузии.
Этот принцип, основанный на идеях неравновесной термодинамики и методе Монте-Карло, заставляет генерируемое…
Этот принцип, основанный на идеях неравновесной термодинамики и методе Монте-Карло, заставляет генерируемое…
Напоминаю, что у каждого моего поста есть теги, по которым можно смотреть посты определенной тематики, которая вас интересует: например
#сверхпроводимость
#экситоны
#нейронные_сети
#атомные_газы
и так далее. Полный список тегов указан в закрепленном посте.
Тегом #популярное я помечаю посты, для понимания которых не требуется быть специалистом-физиком, хотя некоторые из них содержат формулы. Тегом #объяснения помечены посты, которые могут быть полезны в образовательных целях.
#сверхпроводимость
#экситоны
#нейронные_сети
#атомные_газы
и так далее. Полный список тегов указан в закрепленном посте.
Тегом #популярное я помечаю посты, для понимания которых не требуется быть специалистом-физиком, хотя некоторые из них содержат формулы. Тегом #объяснения помечены посты, которые могут быть полезны в образовательных целях.
👍11
Принцип максимальной энтропии Эдвина Джейнса, называемый также MaxEnt, формулируется следующим образом: при наличии какой-либо информации (условий для средних значений, ограничений, симметрий и т.д.) о распределении вероятности случайной величины p(x) наименее искаженным его выбором является распределение, удовлетворяющее этим условиям и одновременно дающее максимальную энтропию Шеннона S = –∫dx p(x) ln(x).
«Наименее искаженный» здесь означает не только «наиболее правильный с теоретических позиций», но и «наилучшим образом согласующийся с экспериментальными данными». Принцип максимальной энтропии не следует путать со вторым началом термодинамики, где тоже говорится о стремлении энтропии к максимуму, но в другом контексте.
Неформально принцип MaxEnt можно сформулировать так: у нас имеется какая-то фрагментарная информация о статистическом распределении – например, мы знаем только его среднее значение или какие-нибудь симметрии. Следовательно, нам нужно наложить на распределение ограничения, вытекающие из этой информации, а по всем остальным параметрам распределения максимизировать наше незнание о нем, то есть энтропию S. Если же энтропия будет не максимальной, то это будет означать, что мы, при задании распределения p(x), фактически использовали некую дополнительную информацию о нем – на что не имели оснований! – а значит, исказили его форму.
Если наложенные на p(x) условия линейны по самому распределению, то оно может быть легко найдено максимизацией S как функционала p(x) с наложением условий методом неопределенных множителей Лагранжа. В частности, при задании только среднего значения <x> максимальную энтропию имеет экспоненциальное распределение p(x) ~ exp(–ax). Если известны среднее значение и дисперсия, оптимальным является гауссово распределение.
Важно, что MaxEnt – не просто философский принцип, указывающей нам, «как правильно мыслить», а вполне рабочий инструмент. Часто бывает, что о статистике величины или группы связанных величин мы имеем лишь обрывочную информацию, а нужно посчитать производные этой статистики, требующие знания полного распределения. Здесь принцип максимальной энтропии дает рецепт того, как действовать, чтобы меньше всего ошибиться.
Вот пример: в методике оценки ошибок экспериментов, которой учат на 1-м курсе физфака, используется как раз принцип MaxEnt. А именно, когда по данным многократных измерений величины мы узнаем ее среднее значение и дисперсию, мы в дальнейшем считаем ее гауссово распределенной с этими же средним и дисперсией. Почему выбирается именно гауссово распределение? Такой выбор можно обосновать центральной предельной теоремой: если на результат измерения оказывает влияние большое число независимых факторов, то распределение должно быть гауссовым. Но далеко не факт, что условия применимости этой теоремы выполняются в каждом конкретном случае. Здесь нам на помощь приходит принцип MaxEnt: если считать, что, кроме среднего и дисперсии, другой информации о случайной величине у нас нет, то гауссово распределение будет наиболее правильным выбором.
#объяснения #математика #стохастическая_термодинамика
«Наименее искаженный» здесь означает не только «наиболее правильный с теоретических позиций», но и «наилучшим образом согласующийся с экспериментальными данными». Принцип максимальной энтропии не следует путать со вторым началом термодинамики, где тоже говорится о стремлении энтропии к максимуму, но в другом контексте.
Неформально принцип MaxEnt можно сформулировать так: у нас имеется какая-то фрагментарная информация о статистическом распределении – например, мы знаем только его среднее значение или какие-нибудь симметрии. Следовательно, нам нужно наложить на распределение ограничения, вытекающие из этой информации, а по всем остальным параметрам распределения максимизировать наше незнание о нем, то есть энтропию S. Если же энтропия будет не максимальной, то это будет означать, что мы, при задании распределения p(x), фактически использовали некую дополнительную информацию о нем – на что не имели оснований! – а значит, исказили его форму.
Если наложенные на p(x) условия линейны по самому распределению, то оно может быть легко найдено максимизацией S как функционала p(x) с наложением условий методом неопределенных множителей Лагранжа. В частности, при задании только среднего значения <x> максимальную энтропию имеет экспоненциальное распределение p(x) ~ exp(–ax). Если известны среднее значение и дисперсия, оптимальным является гауссово распределение.
Важно, что MaxEnt – не просто философский принцип, указывающей нам, «как правильно мыслить», а вполне рабочий инструмент. Часто бывает, что о статистике величины или группы связанных величин мы имеем лишь обрывочную информацию, а нужно посчитать производные этой статистики, требующие знания полного распределения. Здесь принцип максимальной энтропии дает рецепт того, как действовать, чтобы меньше всего ошибиться.
Вот пример: в методике оценки ошибок экспериментов, которой учат на 1-м курсе физфака, используется как раз принцип MaxEnt. А именно, когда по данным многократных измерений величины мы узнаем ее среднее значение и дисперсию, мы в дальнейшем считаем ее гауссово распределенной с этими же средним и дисперсией. Почему выбирается именно гауссово распределение? Такой выбор можно обосновать центральной предельной теоремой: если на результат измерения оказывает влияние большое число независимых факторов, то распределение должно быть гауссовым. Но далеко не факт, что условия применимости этой теоремы выполняются в каждом конкретном случае. Здесь нам на помощь приходит принцип MaxEnt: если считать, что, кроме среднего и дисперсии, другой информации о случайной величине у нас нет, то гауссово распределение будет наиболее правильным выбором.
#объяснения #математика #стохастическая_термодинамика
🔥1
Вот простейшие примеры использования принципа MaxEnt для вывода распределений дискретной величины в тех случаях, когда известны либо ее среднее значение, либо среднее значение и дисперсия.
Мы устремляем к максимуму энтропию Шеннона S распределения, накладывая при этом дополнительные условия: нормировки суммы вероятностей на единицу, а также равенства среднего значения (и, при необходимости, дисперсии) заданным величинам. Делая это при помощи метода неопределенных множителей Лагранжа, мы находим экстремум расширенного функционала Ω = S – (сумма наложенных условий, умноженных на соответствующие неопределенные множители λ).
В рассматриваемых случаях все наложенные условия линейны по вероятностям, поэтому экстремум Ω находится очень просто, и мы сразу получаем явные выражения для распределений.
#объяснения #математика #стохастическая_термодинамика
Мы устремляем к максимуму энтропию Шеннона S распределения, накладывая при этом дополнительные условия: нормировки суммы вероятностей на единицу, а также равенства среднего значения (и, при необходимости, дисперсии) заданным величинам. Делая это при помощи метода неопределенных множителей Лагранжа, мы находим экстремум расширенного функционала Ω = S – (сумма наложенных условий, умноженных на соответствующие неопределенные множители λ).
В рассматриваемых случаях все наложенные условия линейны по вероятностям, поэтому экстремум Ω находится очень просто, и мы сразу получаем явные выражения для распределений.
#объяснения #математика #стохастическая_термодинамика
Стоит отметить, что принцип MaxEnt является обобщением принципа недостаточного основания Лапласа.
Принцип недостаточного основания Лапласа, называемый также principle of indifference, можно сформулировать так: в отсутствие какой-либо информации о случайном событии все его варианты нужно считать равновероятными.
Пример использования такого принципа можно встретить в известном анекдоте «про блондинку и динозавра», где утверждается, что вероятность встретить на улице динозавра равна 1/2, потому что мы его «либо встретим, либо не встретим». Казалось бы, это абсурдное предсказание, не согласующееся с повседневной практикой, потому что на самом деле вероятность встретить динозавра на улице исчезающе мала.
Но, если подумать, откуда мы делаем вывод о малости такой вероятности? Такой вывод мы делаем на основании массы информации: мы знаем, кто такие динозавры; что они жили когда-то давно на Земле, но потом вымерли; а если они вымерли, то сами собой обратно не воскреснут; и так далее. Считая, что количество такой информации равно N бит (причем N >> 1), вероятность встретить динозавра можно оценить как 2⁻ᴺ – это и правда очень маленькая величина. Если же мы вообще ничего не знаем о динозаврах, то ответ 1/2 будет наиболее правильным.
Есть и более серьезные примеры использования принципа недостаточного основания Лапласа. Например, почему мы считаем, что вероятности выпадения орла и решки при бросании «честной» монетки равны 1/2? Потому что такая монетка симметрична, так что у нас нет никакой информации, позволяющей предпочесть орла решке или наоборот. Следовательно, наиболее правильным выбором вероятностей будет 1/2 и 1/2. То же самое касается вероятностей выпадения различных чисел на игральном кубике: коль скоро он симметричен, у нас нет никакой информации о распределении вероятностей помимо условия нормировки суммы 6 вероятностей на единицу. Поэтому мы должны считать, что все эти вероятности равны между собой и составляют 1/6. И что самое интересное, предсказания принципа Лапласа действительно согласуются с экспериментами.
Принцип MaxEnt отличается от принципа Лапласа в том смысле, что он отвечает на вопрос: а что делать, если какая-то информация о распределении вероятностей у нас таки есть? В этом случае наиболее непредвзятым будет распределение вероятностей, совместимое с имеющейся информацией и одновременно максимизирующее энтропию. Использование распределения с меньшей энтропией будет означать, что, фактически, мы сделали дополнительные предположения о его природе, для которых у нас нет оснований.
#объяснения #математика #стохастическая_термодинамика
Принцип недостаточного основания Лапласа, называемый также principle of indifference, можно сформулировать так: в отсутствие какой-либо информации о случайном событии все его варианты нужно считать равновероятными.
Пример использования такого принципа можно встретить в известном анекдоте «про блондинку и динозавра», где утверждается, что вероятность встретить на улице динозавра равна 1/2, потому что мы его «либо встретим, либо не встретим». Казалось бы, это абсурдное предсказание, не согласующееся с повседневной практикой, потому что на самом деле вероятность встретить динозавра на улице исчезающе мала.
Но, если подумать, откуда мы делаем вывод о малости такой вероятности? Такой вывод мы делаем на основании массы информации: мы знаем, кто такие динозавры; что они жили когда-то давно на Земле, но потом вымерли; а если они вымерли, то сами собой обратно не воскреснут; и так далее. Считая, что количество такой информации равно N бит (причем N >> 1), вероятность встретить динозавра можно оценить как 2⁻ᴺ – это и правда очень маленькая величина. Если же мы вообще ничего не знаем о динозаврах, то ответ 1/2 будет наиболее правильным.
Есть и более серьезные примеры использования принципа недостаточного основания Лапласа. Например, почему мы считаем, что вероятности выпадения орла и решки при бросании «честной» монетки равны 1/2? Потому что такая монетка симметрична, так что у нас нет никакой информации, позволяющей предпочесть орла решке или наоборот. Следовательно, наиболее правильным выбором вероятностей будет 1/2 и 1/2. То же самое касается вероятностей выпадения различных чисел на игральном кубике: коль скоро он симметричен, у нас нет никакой информации о распределении вероятностей помимо условия нормировки суммы 6 вероятностей на единицу. Поэтому мы должны считать, что все эти вероятности равны между собой и составляют 1/6. И что самое интересное, предсказания принципа Лапласа действительно согласуются с экспериментами.
Принцип MaxEnt отличается от принципа Лапласа в том смысле, что он отвечает на вопрос: а что делать, если какая-то информация о распределении вероятностей у нас таки есть? В этом случае наиболее непредвзятым будет распределение вероятностей, совместимое с имеющейся информацией и одновременно максимизирующее энтропию. Использование распределения с меньшей энтропией будет означать, что, фактически, мы сделали дополнительные предположения о его природе, для которых у нас нет оснований.
#объяснения #математика #стохастическая_термодинамика
Wikipedia
Principle of indifference
in probability theory, a rule for assigning epistemic probabilities
Как-то раз я решил почитать книжку Эли Картана – мне ее рекомендовали как весьма полезную и просвещающую в области дифференциальной геометрии.
Однако мое чтение закончилось на первом же предложении...
#математика #цитаты
Однако мое чтение закончилось на первом же предложении...
#математика #цитаты
😁5🔥2
Экспериментальные исследования графена на различных подложках, имеющих разные величины диэлектрической константы – это интересный метод, позволяющий выявить роль многочастичных эффектов. Подложки с большими диэлектрическими константами сильнее экранируют кулоновское взаимодействие между собственными электронами графена – поэтому, если какие-то наблюдаемые величины меняются при замене подложек, причина их изменения кроется в эффектах взаимодействия.
В этом эксперименте изучалось влияние подложек на спектр рамановского рассеяния графена. Как видно на графике слева, G-линия на спектре рамановского рассеяния нечувствительна к вставке монослоя WSe₂ рядом с графеном, инкаспулированным в гексагональный нитрид бора, а 2D-линия приобретает заметное синее смещение. Справа видно, что это не случайность: при замене окружения графена на все более сильно экранирующие 2D-линия систематически увеличивает свою частоту. Значит, это явно многочастичный эффект, в котором замешано кулоновское взаимодействие.
#графен #фононы
В этом эксперименте изучалось влияние подложек на спектр рамановского рассеяния графена. Как видно на графике слева, G-линия на спектре рамановского рассеяния нечувствительна к вставке монослоя WSe₂ рядом с графеном, инкаспулированным в гексагональный нитрид бора, а 2D-линия приобретает заметное синее смещение. Справа видно, что это не случайность: при замене окружения графена на все более сильно экранирующие 2D-линия систематически увеличивает свою частоту. Значит, это явно многочастичный эффект, в котором замешано кулоновское взаимодействие.
#графен #фононы
👍3
А вот объяснение того, почему (как описано в предыдущем посте) G-линия спектра рамановского рассеяния графена нечувствительна к диэлектрическому окружению, а 2D-линия демонстрирует синее смещение при усилении экранирования кулоновского взаимодействия.
Дело в том, что G-линия появляется благодаря испусканию оптических фононов, имеющих импульс Γ (то есть близкий к нулю) и псевдовекторную симметрию, как показано на рисунке слева. Векторность таких фононов роднит их с электрическим током, который в квантовой электродинамике является сохраняющейся величиной и поэтому не перенормируется за счет взаимодействий.
В то же время, 2D-линия обусловлена двукратным испусканием оптических фононов с импульсами ±K (они перебрасывают электрон в противоположную долину), имеющими скалярную и псевдоскалярную симметрии, как показано на рисунке справа. Имея другую симметрию, такие фононы уже не защищены от перенормировок частот за счет взаимодействий. Поэтому замена подложки приводит к сдвигу их частот.
#графен #фононы
Дело в том, что G-линия появляется благодаря испусканию оптических фононов, имеющих импульс Γ (то есть близкий к нулю) и псевдовекторную симметрию, как показано на рисунке слева. Векторность таких фононов роднит их с электрическим током, который в квантовой электродинамике является сохраняющейся величиной и поэтому не перенормируется за счет взаимодействий.
В то же время, 2D-линия обусловлена двукратным испусканием оптических фононов с импульсами ±K (они перебрасывают электрон в противоположную долину), имеющими скалярную и псевдоскалярную симметрии, как показано на рисунке справа. Имея другую симметрию, такие фононы уже не защищены от перенормировок частот за счет взаимодействий. Поэтому замена подложки приводит к сдвигу их частот.
#графен #фононы
Интересный эксперимент, в котором обнаружен существенно нелинейный и невзаимный кулоновский дрэг (или эффект увлечения) между электронами в двух полупроводниковых квантовых нитях. Как показано на рисунке сверху, квантовые нити образуются выталкиванием электронов из полупроводниковой квантовой ямы наложенными сверху затворными электродами (верхним, нижним и центральным), на которые подается отрицательный потенциал. При этом, изменяя потенциалы верхнего и нижнего затворов, можно управлять уровнями Ферми в каждой нити.
Невзаимность продемонстрирована на диаграммах снизу: когда нижняя нить является активной (через нее пропускается ток), а верхняя пассивной (в ней измеряется напряжение, обусловленное увлечением электронов током активной нити), мы наблюдаем одну картину зависимости величины дрэга от двух затворных напряжений, показанную слева. При перестановке активной и пассивной нитей картина резко меняется, как показано справа.
#твердое_тело #наноструктуры
Невзаимность продемонстрирована на диаграммах снизу: когда нижняя нить является активной (через нее пропускается ток), а верхняя пассивной (в ней измеряется напряжение, обусловленное увлечением электронов током активной нити), мы наблюдаем одну картину зависимости величины дрэга от двух затворных напряжений, показанную слева. При перестановке активной и пассивной нитей картина резко меняется, как показано справа.
#твердое_тело #наноструктуры