Краевые дислокации – это дефекты кристаллической структуры в виде линий, на которых одна из атомных плоскостей резко обрывается. Будучи топологическими дефектами, линии дислокаций не могут просто так рассосаться, но зато могут перемещаться по кристаллу. Как видно на рисунке, проход дислокации от одного края кристалла до другого приводит к его сдвиговой деформации – вот почему наличие дислокаций заметно снижает прочность металлов, делая их текучими под нагрузкой.

Казалось бы, самый очевидный способ сделать металл более упругим и менее текучим – это попытаться избавиться от дислокаций. Но технически это очень сложно. Поэтому испокон веков кузнецы для упрочнения металлов применяли противоположный подход: создать в кристаллической решетке как можно больше дислокаций и запутать их. Линии дислокаций отталкиваются друг от дружки – поэтому, множество раз деформируя металлическую полоску, расплющивая ее и складывая, можно добиться того, что дислокации перепутаются и лишатся подвижности.

#твердое_тело #популярное

Параксиальное распространение света через материал с показателем преломления, медленно меняющимся вдоль направления распространения, позволяет реализовывать аналог эволюции волновой функции согласно уравнению Шредингера, где роль времени играет координата вдоль светового пучка.

Если материал обладает кубической оптической нелинейностью, то вместо уравнения Шредингера можно реализовывать нелинейное уравнение Гросса-Питаевского, где волна взаимодействует сама с собой. Точнее, мы имеем дело с системой двух связанных уравнений Гросса-Питаевского для волн разных поляризаций. В этой работе теоретически показано, что если материал обладает неоднородностью спиральной формы, это заставляет волновой пакет вращаться, как если бы система была помещена во вращающийся сосуд.

На диаграммах для поляризации и фазы волновой функции можно видеть, как при таком вращении образуются квантованные вихри. Получается, что полностью оптическая система демонстрирует черты сверхтекучего поведения.

#фотоника #сверхтекучесть

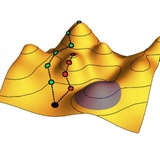
Это пример решетки взаимодействующих кубитов, реализующих поверхностный код (surface code) – метод коррекции ошибок, оптимизированный для расположения кубитов на плоскости.

Основные кубиты, несущие информацию, показаны здесь зелеными кругами, а синими треугольниками и красными крестиками обозначены вспомогательные кубиты, служащие для контроля четности числа возбуждений и относительных фаз. А именно, каждый кубит контроля четности числа возбуждений (треугольник) несет в себе информацию о величине <Z₁Z₂> двух соединенных с ним основных кубитов. Если величина Z у одного из них перевернется, это можно будет отследить по состоянию вспомогательного кубита и потом скорректировать. Аналогично, кубит контроля относительной фазы (крестик) несет информацию о величине < X₁X₂>, которая изменится при случайном перевороте относительной фазы двух основных кубитов.

Серыми областями на рисунке показаны схемы проведенных экспериментов, где отрабатывалась коррекция ошибок при помощи поверхностного кода.

#квантовые_вычисления

Красивый эксперимент, в котором двумерный бозе-конденсат атомов размешивался лазерным лучом и по тому, нагрелся ли он за счет диссипации, делался вывод о наличии или отсутствии в нем сверхтекучести.

Как видно на графиках, при начальной температуре атомного облака выше критической его температура после размешивания повышается – причем тем сильнее, чем выше скорость вращения лазерного луча. Это проявление обычного трения, переводящего работу лазерного луча в тепло. Если же начальная температура была ниже критической, то до определенного порога скорости температура не повышается, потому что атомное облако, будучи сверхтекучим, не увлекается лучом и не поддерживает диссипацию энергии. Только при превышении критической скорости температура начинает повышаться.

Кстати говоря, нормальная компонента – поддерживающая обычную диссипацию – во втором случае тоже присутствует, но не проявляется из-за того, что оттеснена на периферию облака, куда лазерный луч не достает.

#атомные_газы #сверхтекучесть

А здесь можно полюбоваться на зонную структуру оксида индия In₂O₃.

Слева – зонная структура, посчитанная методом функционала плотности с учетом U-члена (локального отталкивания электронов на узле) и спин-орбитального взаимодействия. Справа найденная отсюда теоретическая плотность электронных состояний сравнивается с экспериментами по фотоэлектронной спектроскопии.

Включение U-члена и спин-орбитального взаимодействия оказывается очень важным для правильного воспроизведения экспериментальных данных: без них не происходит нужной гибридизации 2s-электронов кислорода и 4d-электронов индия, дающей относительно малую щель между двумя нижними зонами.

#твердое_тело

Иерархия доминирования в стаей голубей определяется тем, кто в какой очередности они принимают пищу, кто кого гоняет (доминирующий голубь движется на подчиненного, а тот пытается избежать сближения) и кто кого клюет. Но у них есть и вторая, параллельная иерархия лидерства, проявляющаяся при полете: лидирующие голуби задают направление полета стаи, а остальные за ними следуют.

В этой работе изучили иерархии доминирования и лидерства в трех стаях голубей при помощи автоматического трекинга и программной обработки видеозаписей. Оказалось, что иерархии доминирования и лидерства никак не связаны между собой и существуют параллельно – видимо, потому, что они требуют от голубей разных, не связанных друг с другом компетенций. Это демонстрируется на диаграммах снизу, где красным и зеленым цветом показано доминирование – иерархии приема пищи и клевания, – а синим цветом показана иерархия лидерства в полете. Как видно, красно-зеленая структура никак не скоррелирована с синей.

#биология #популярное #общество

Еще несколько фактов насчет иерархий в стае голубей:

• Блокирование приема пищи демонстрирует довольно сильную степень взаимности: если голубь A систематически блокирует доступ голубя B к кормушке (и, таким образом является доминирующим), то голубь B тоже довольно часто (хотя и в меньшем числе случаев) будет блокировать доступ голубю A.

• Все изученные иерархические отношения – приема пищи, избегания сближений, драк и клевания, лидерства в полете – у голубей оказались транзитивными. Это значит, что если голубь A доминирует (или лидирует) над голубем B, а голубь B доминирует над голубем C, то A доминирует над C. Иными словами, иерархические отношения не имеют замкнутых циклов вида A → B → C → A, при которых угнетение могло бы идти по кругу.

• То, что иерархии силового доминирования и лидерства в полете у голубей независимы – нетривиальный факт. Например, у волков и павианов эти две иерархии почти совпадают: самые сильные доминирующие особи являются одновременно и лидерами при стайном перемещении. Вероятно, особенность голубей здесь в том, что в полете невозможно устраивать драки и прочие взаимодействия, на которых строится силовое доминирование, поэтому на первый план выступают другие компетенции – знание местности, способность ориентироваться и хорошая память.

#биология #популярное #общество

Вот одно из проявлений универсальности фазовых переходов. Как мы знаем, плотность жидкости и плотность полученного из нее пара сильно различаются, даже когда они находятся во взаимном равновесии, при одной и той же температуре.

Однако, когда температура превышает критическую (для воды, к примеру, это около 374 °C), различие между жидкостью и газом пропадает. Если нарисовать плотности ρ жидкости и пара как функции температуры T, причем плотности взять в единицах плотности ρ_c в критической точке, а температуру – в единицах критической температуры T_c, то все зависимости для разных жидкостей укладываются на одну и ту же кривую.

Причина такой универсальности – независимости от химического состава, деталей свойств и взаимодействий молекул жидкостей – в том, что в точке фазового перехода между жидкостью и газом ключевую роль играет предельно крупномасштабное поведение системы, а не ее микроскопические детали.

#термодинамика #популярное #объяснения

Любопытное теоретическое исследование активной материи в виде множества вытянутых стержней, самостоятельно движущихся вдоль своей оси и помещенных на поверхность сферы.

Сверху на рисунке представлена фазовая диаграмма системы в переменных плотности стержней (по горизонтали) и их пропорций – отношения длины к ширине (по вертикали). Структура фаз проиллюстрирована снизу. Помимо обычных газа и жидкости, существует фаза изолированных скоплений, специфичная именно для активных частиц: двигаясь вдоль своей оси, стержни сталкиваются и застревают, образуя скопления. При большей плотности сгустки соединяются в единый кристалл-нематик, но в нем неизбежно присутствуют дефекты: из за «теоремы о причесывании ежа» на сфере невозможно создать выровненную структуру без топологических дефектов.

Стекло – тоже интересная фаза в случае активной материи. Хотя стержни запутываются в полностью аморфную структуру, из-за комбинация движущих сил заставляет ее вращаться как единое целое вокруг оси сферы.

#самоорганизация #стекла

А вот, для сравнения, что происходит в случае таких же активных частиц в форме вытянутых стержней, но помещенных на плоскую поверхность. Главное отличие от системы, описанной в предыдущем посте – это существование выстроенной фазы, называемой здесь словом “laning”.

Это фаза, в которой стержни выстроены в параллельные ряды, причем разные ряды движутся в случайных направлениях – похоже на многополосную автомобильную дорогу, отсюда и название. На сфере, в отличие от плоской поверхности, такая фаза невозможна из-за «теоремы о причесывании ежа».

#самоорганизация #стекла

Полезная статья о том, как квантовые геометрические эффекты влияют на функции отклика сверхпроводников. Как я писал раньше, сильнее всего квантовая геометрия проявляется в случае плоских энергетических зон, когда геометрические вклады, например, в сверхтекучую плотность – единственное, что остается отличным от нуля. В общем случае нужно рассматривать как традиционные вклады, обусловленные дисперсией, так и геометрические вклады, обусловленные структурой волновых функций.

Авторы проводят расчеты, отталкиваясь от среднеполевого гамильтониана сверхпроводника, содержащего спаривающий потенциал – члены, пропорциональные cc и c⁺c⁺. Нетривиальная геометрия электронных состояний меняет и структуру такого потенциала, что отражается на последующих расчетах термодинамического потенциала и функций отклика.

На рисунке показан простой пример формул для термодинамического потенциала сверхпроводника Ω, состоящего из обычных пара- и диамагнитных вкладов, и дополнительного геометрического вклада.

#сверхпроводимость

Ничего себе, сколько грантов в благодарностях всего у двух авторов статьи! А у нас требуют, чтобы каждая статья была поддержана только одним грантом, иначе не засчитывают ее при отчете...

#цитаты

Сингулярности Ван Хова – это особенности (изломы, разрывы и интегрируемые сингулярности) зависимости плотности состояний от энергии, возникающие в кристалле из-за критических точек, то есть точек в пространстве квазиимпульса, где первая производная электронной дисперсии обращается в ноль. В зависимости от поведения матрицы вторых производных, в них имеются максимумы, минимумы или седловые точки дисперсии.

Но бывают сингулярности Ван Хова высшего порядка, где обращаются в ноль не только первые, но и вторые производные. К примеру, в двумерном материале седловая точка (обычная сингулярность Ван Хова) дает логарифмический пик в плотности состояний ρ(E) ~ ln|E – Eₒ|, а сингулярность Ван Хова высшего порядка дает более сильный, степенной пик ρ(E) ~ |E – Eₒ|⁻¹ᐟ⁴.

В этой работе показано, что зонная структура электронов на поверхности Sr₂RuO₄, подвергающейся кристаллической реконструкции, довольно близка к появлению сингулярности Ван Хова высшего порядка на уровне Ферми.

#твердое_тело

Хорошая иллюстрация того, что происходит с химическим потенциалом и концентрацией электронов в допированном полупроводнике при разных температурах .

Химический потенциал μ определяется подгонкой суммарного числа электронов под распределение Ферми-Дирака 1/{exp[(E – μ)/T] + 1}, умноженное на плотность состояний и проинтегрированное по энергии. При низких температурах T → 0 химический потенциал превращается в уровень Ферми μ = E_F, и в случае полупроводника n-типа он располагается между заполненными энергетическими уровнями донорных примесей E_D и краем незаполненной зоны проводимости E_C.

При промежуточных температурах E_C – E_D << T < E_g примеси ионизуются, за счет чего в зоне проводимости образуется почти постоянная концентрация электронов n. При высоких температурах T >> E_g, превышающих щель, химический потенциал располагается уже внутри основной щели (как в недопированном полупроводнике), а концентрация электронов n растет благодаря их тепловой активации из валентной зоны.

#твердое_тело #объяснения

В этой работе предложен интересный способ измерения невзаимного электромагнитного отклика материалов и наноструктур. Авторы предлагают помещать исследуемый образец на перекрестье двух электромагнитных резонаторов, так что недиагональные компоненты его диэлектрической восприимчивости χ_xy и проводимости σ_xy связывают фотонные моды в этих резонаторах между собой.

От операторов фотонов a и b в двух резонаторах при помощи преобразования Швингера можно перейти к эффективным операторам спина S_x = ½(a⁺b + b⁺a), S_x = ½(ia⁺b – ib⁺a), S_z = ½(a⁺a – b⁺b), длина которого сохраняется при сохранении полного числа фотонов a⁺a + b⁺b. Такой спин, в ходе своей эволюции с течением времени, подвергается действию эффективного магнитного поля с компонентами {χ_xy, σ_xy, Δω}, где Δω – расстройка частот резонаторов. Поэтому, приготавливая заданные квантовые состояния фотонов в двух резонаторах и регистрируя их эволюцию за определенный промежуток времени, можно проводить очень точные измерения χ_xy и σ_xy.

#фотоника

Для того, чтобы методом обратной диффузии генерировать изображения, принадлежащие к определенному классу, можно использовать направление при помощи классификатора или направление без классификатора – второй способ сейчас является общепринятым.

Но как генерировать изображения, не принадлежащие к одному из нескольких жестко разделенных классов, а по текстовому описанию свободного формата? Общий принцип здесь примерно такой же, как при направлении обратной диффузии без использования классификатора: в ходе обучения нейросети мы подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она могла воспроизводить случайный гауссов шум при любых значениях аргументов – текущего изображения x, метки его класса y и номера шага диффузии t. Только вместо дискретных меток класса y можно использовать любой результат «переваривания» текстовых фраз языковой моделью – отдельной нейросетью, превращающей текстовую фразу z в высокоуровневую информацию y о ее содержании, называемую вложением (embedding).

Таким образом, процесс обучения нейросети, генерирующей изображения по текстовому описанию, выглядит, в общих чертах, следующим образом:
• Берем предварительно обученную языковую модель-кодировщик, умеющую превращать любую текстовую строку z в ее переработанное вложение y.
• Берем нейросеть, позволяющую достаточно гибко подгонять функцию ϵ_θ(x, y, t) трех аргументов – x (изображения), y (вложения текстовой фразы) и t (номера шага диффузии).
• Добываем библиотеку обучающих примеров – пар изображений xᵢ⁽⁰⁾ и прилагающихся к ним текстовых описаний zᵢ.
• Используя эту библиотеку, подгоняем функцию ϵ_θ(x, y, t) таким образом, чтобы она минимизировала ошибку ||ϵ_θ(x, y, t) – ϵ||² – отклонение от случайного гауссового шума ϵ, при этом аргументы x и y строятся на элементах обучающей выборки: x является линейной комбинацией xᵢ⁽⁰⁾ и ϵ с коэффициентами, зависящими от t, а y вычисляется языковой моделью на основе zᵢ.
• После того, как функция ϵ_θ(x, y, t) обучена, нейросеть готова к работе: по любому новому текстовому описанию z языковая модель генерирует его вложение y, а затем с этим аргументом функция ϵ_θ(x, y, t) используется для «отмены» шума на каждом шаге обратной диффузии.

Нейросеть Imagen от корпорации Google использует такой метод генерации изображения на основе текстовой модели T5. Другая нейросеть – ее конкурент GLIDE от компании OpenAI – используeт вместо этого CLIP-вложения. А именно, в качестве аргумента y используется не просто результат переработки текстовой строки, а ее перекрытие с результатом переработки текущего изображения x. Похожим образом работает нейросеть unCLIP, также от компании OpenAI. Нейросеть eDiff-I от корпорации Nvidia для направления обратной диффузии применяет комбинацию текстовой модели T5 и CLIP-вложений: первая в большей степени используется на ранних этапах генерации, вторая – с большим весом на поздних этапах.

#нейронные_сети #популярное

Напоминаю, что у каждого моего поста есть теги, по которым можно смотреть посты определенной тематики, которая вас интересует: например
#сверхпроводимость
#экситоны
#нейронные_сети
#атомные_газы
и так далее. Полный список тегов указан в закрепленном посте.

Тегом #популярное я помечаю посты, для понимания которых не требуется быть специалистом-физиком, хотя некоторые из них содержат формулы. Тегом #объяснения помечены посты, которые могут быть полезны в образовательных целях.

Принцип максимальной энтропии Эдвина Джейнса, называемый также MaxEnt, формулируется следующим образом: при наличии какой-либо информации (условий для средних значений, ограничений, симметрий и т.д.) о распределении вероятности случайной величины p(x) наименее искаженным его выбором является распределение, удовлетворяющее этим условиям и одновременно дающее максимальную энтропию Шеннона S = –∫dx p(x) ln(x).

«Наименее искаженный» здесь означает не только «наиболее правильный с теоретических позиций», но и «наилучшим образом согласующийся с экспериментальными данными». Принцип максимальной энтропии не следует путать со вторым началом термодинамики, где тоже говорится о стремлении энтропии к максимуму, но в другом контексте.

Неформально принцип MaxEnt можно сформулировать так: у нас имеется какая-то фрагментарная информация о статистическом распределении – например, мы знаем только его среднее значение или какие-нибудь симметрии. Следовательно, нам нужно наложить на распределение ограничения, вытекающие из этой информации, а по всем остальным параметрам распределения максимизировать наше незнание о нем, то есть энтропию S. Если же энтропия будет не максимальной, то это будет означать, что мы, при задании распределения p(x), фактически использовали некую дополнительную информацию о нем – на что не имели оснований! – а значит, исказили его форму.

Если наложенные на p(x) условия линейны по самому распределению, то оно может быть легко найдено максимизацией S как функционала p(x) с наложением условий методом неопределенных множителей Лагранжа. В частности, при задании только среднего значения <x> максимальную энтропию имеет экспоненциальное распределение p(x) ~ exp(–ax). Если известны среднее значение и дисперсия, оптимальным является гауссово распределение.

Важно, что MaxEnt – не просто философский принцип, указывающей нам, «как правильно мыслить», а вполне рабочий инструмент. Часто бывает, что о статистике величины или группы связанных величин мы имеем лишь обрывочную информацию, а нужно посчитать производные этой статистики, требующие знания полного распределения. Здесь принцип максимальной энтропии дает рецепт того, как действовать, чтобы меньше всего ошибиться.

Вот пример: в методике оценки ошибок экспериментов, которой учат на 1-м курсе физфака, используется как раз принцип MaxEnt. А именно, когда по данным многократных измерений величины мы узнаем ее среднее значение и дисперсию, мы в дальнейшем считаем ее гауссово распределенной с этими же средним и дисперсией. Почему выбирается именно гауссово распределение? Такой выбор можно обосновать центральной предельной теоремой: если на результат измерения оказывает влияние большое число независимых факторов, то распределение должно быть гауссовым. Но далеко не факт, что условия применимости этой теоремы выполняются в каждом конкретном случае. Здесь нам на помощь приходит принцип MaxEnt: если считать, что, кроме среднего и дисперсии, другой информации о случайной величине у нас нет, то гауссово распределение будет наиболее правильным выбором.

#объяснения #математика #стохастическая_термодинамика