Статья о социальной термодинамике 2.0, посвященная памяти Карла Маркса.
При помощи уравнения Ван-дер-Ваальса автор описывает переход от капитализма к коммунизму по мере развития производительных сил. При низком уровне их развития (что отвечает низкой температуре) у нас сосуществуют два общественных класса – пролетариат и буржуазия, – что отвечает разделению жидкой и газообразной фаз. При высоком же уровне развития производительных сил противоречия между классами стираются и наступает коммунизм, подобно тому, как при сверхкритической температуре исчезает различие между жидкостью и газом.
#термодинамика #общество #цитаты
При помощи уравнения Ван-дер-Ваальса автор описывает переход от капитализма к коммунизму по мере развития производительных сил. При низком уровне их развития (что отвечает низкой температуре) у нас сосуществуют два общественных класса – пролетариат и буржуазия, – что отвечает разделению жидкой и газообразной фаз. При высоком же уровне развития производительных сил противоречия между классами стираются и наступает коммунизм, подобно тому, как при сверхкритической температуре исчезает различие между жидкостью и газом.
#термодинамика #общество #цитаты
😁5🌚3
Квазиклассическое квантование Бора-Зоммерфельда подразумевает, что действие вдоль замкнутой траектории должно квантоваться как ∮p•dr = 2πħ(n+1/2), откуда можно найти квантованные энергии. В этой работе квазиклассическое квантование обобщено на системы с неэрмитовым гамильтонианом H и комплексным спектром энергий.
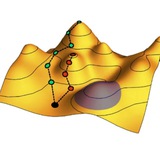
При этом классическая траектория движения, задаваемая вторым законом Ньютона d²r/dt² = –∂H/∂p, будет также комплексной. Авторы показывают, что для того, чтобы такая траектория – хоть и комплексная – была замкнутой, шаги во времени dt тоже должны быть комплексными. Найдя замкнутую траекторию в комплексном пространстве r, проходимую системой за комплексный период времени, можно найти квазиклассический спектр комплексных же энергий.
На рисунке показан пример комплексного осциллятора с комплексной частотой колебаний: при движении в комплексном времени (слева) траектория может быть сделана замкнутой, а при движении в вещественном времени (справа) замкнуть ее невозможно.
#неэрмитовы_системы
При этом классическая траектория движения, задаваемая вторым законом Ньютона d²r/dt² = –∂H/∂p, будет также комплексной. Авторы показывают, что для того, чтобы такая траектория – хоть и комплексная – была замкнутой, шаги во времени dt тоже должны быть комплексными. Найдя замкнутую траекторию в комплексном пространстве r, проходимую системой за комплексный период времени, можно найти квазиклассический спектр комплексных же энергий.
На рисунке показан пример комплексного осциллятора с комплексной частотой колебаний: при движении в комплексном времени (слева) траектория может быть сделана замкнутой, а при движении в вещественном времени (справа) замкнуть ее невозможно.
#неэрмитовы_системы
👍2
Статистика энергий ε = ħ²k²/2m и импульсов k частиц в идеальном бозе- или ферми-газе описывается распределениями Бозе-Эйнштейна и Ферми-Дирака n(k) = [exp{(ħ²k²/2m – μ)/T} ∓ 1]⁻¹, которые подразумевают очень быстрое (гауссово) убывание в пределе больших импульсов k → ∞. Но в газе взаимодействующих частиц это уже не так: если взаимодействие, как часто бывает в атомных газах, является короткодействующим и описывается эффективной длиной рассеяния, то асимптотика чисел заполнения при k → ∞ имеет вид n(k) = С/k⁴.
Коэффициент пропорциональности C называется контактом Тана (Tan’s contact). Примечательно, что он связан с производной полной энергии газа по длине рассеяния аналогом теоремы вириала. В этом эксперименте асимптотика чисел заполнения и, соответственно, контакт Тана для бозе-конденсата атомов в ловушке были измерены с довольно высокой точностью. На графике можно видеть сравнение между теорией и экспериментом для ловушек разной формы и разных методов измерения.
#атомные_газы #бозе_конденсация
Коэффициент пропорциональности C называется контактом Тана (Tan’s contact). Примечательно, что он связан с производной полной энергии газа по длине рассеяния аналогом теоремы вириала. В этом эксперименте асимптотика чисел заполнения и, соответственно, контакт Тана для бозе-конденсата атомов в ловушке были измерены с довольно высокой точностью. На графике можно видеть сравнение между теорией и экспериментом для ловушек разной формы и разных методов измерения.
#атомные_газы #бозе_конденсация
В этой работе метод обратной диффузии был сформулирован в виде задачи предсказания шума – именно в таком виде он сейчас широко используется для генерации изображений нейронными сетями.
В ходе прямой диффузии x_(t–1) → x_t вектор изображения совершает случайный шаг и одновременно сжимается в меру коэффициента √α_t. Как показано на рисунке, за t шагов эти сжатия и случайные шаги ϵ (то есть шум) накапливаются: начиная c исходной точки x₀, которая берется из библиотеки изображений q(x₀), мы оказываемся в точке x_t.
Дальше идея такая: мы подгоняем функцию ϵ_θ(x_t, t), которая достаточно гибкая и генерируется нейросетью, таким образом, чтобы при всех x₀ из обучающей выборки и при любых количествах шагов t она предсказывала случайный гауссов шум ϵ. Для этого при обучении минимизируется функция ошибок L_simple. При обратной же диффузии (sampling) на каждом шаге x_t → x_(t–1) мы осуществляем перемасштабирование и вычитаем ϵ_θ(x_t, t), отменяя шум – это называется словом denoising.
#нейронные_сети #объяснения
В ходе прямой диффузии x_(t–1) → x_t вектор изображения совершает случайный шаг и одновременно сжимается в меру коэффициента √α_t. Как показано на рисунке, за t шагов эти сжатия и случайные шаги ϵ (то есть шум) накапливаются: начиная c исходной точки x₀, которая берется из библиотеки изображений q(x₀), мы оказываемся в точке x_t.
Дальше идея такая: мы подгоняем функцию ϵ_θ(x_t, t), которая достаточно гибкая и генерируется нейросетью, таким образом, чтобы при всех x₀ из обучающей выборки и при любых количествах шагов t она предсказывала случайный гауссов шум ϵ. Для этого при обучении минимизируется функция ошибок L_simple. При обратной же диффузии (sampling) на каждом шаге x_t → x_(t–1) мы осуществляем перемасштабирование и вычитаем ϵ_θ(x_t, t), отменяя шум – это называется словом denoising.
#нейронные_сети #объяснения
Для обучения нейросетей генерации изображений по текстовым описаниям нужны большие библиотеки референсов: готовых изображений с прилагающимся к ним текстами.
Здесь исследователи проанализировали одну из таких новых библиотек и пришли в ужас: посмотрите сами, какие изображения в этой библиотеке привязаны к фразам "best president" и "worst president"!
#цитаты #нейронные_сети
Здесь исследователи проанализировали одну из таких новых библиотек и пришли в ужас: посмотрите сами, какие изображения в этой библиотеке привязаны к фразам "best president" и "worst president"!
#цитаты #нейронные_сети
Вот это крутой эксперимент, в котором реализованы короткие пути к адиабатичности – невозможный в классической термодинамике способ быстро изменить состояние квантовой системы без потери энергий на диссипацию.
Газ атомов-фермионов ⁶Li помещался в вытянутую гармоническую ловушку, которая затем быстро сжималась в 4 раза до сферической формы. Обычно при этом происходит возбуждение атомного газа с совершением дополнительной работы. Но если частоты ловушки в направлении сжатия ω_x и в двух других направлениях ω_y = ω_z менять по определенному протоколу, показанному на графиках синими точками, то возбуждения газа удается избежать. Здесь помогает масштабная инвариантность ферми-газа в унитарном режиме.
На графике снизу показана измеренная неадиабатическая работа Q* – превышение реально совершаемой работы над идеальным адиабатическим пределом. При использовании короткого пути к адиабатичности в конце протокола она зануляется, а при наивном сжатии (коричневые точки) – нет.
#атомные_газы #квантовая_термодинамика
Газ атомов-фермионов ⁶Li помещался в вытянутую гармоническую ловушку, которая затем быстро сжималась в 4 раза до сферической формы. Обычно при этом происходит возбуждение атомного газа с совершением дополнительной работы. Но если частоты ловушки в направлении сжатия ω_x и в двух других направлениях ω_y = ω_z менять по определенному протоколу, показанному на графиках синими точками, то возбуждения газа удается избежать. Здесь помогает масштабная инвариантность ферми-газа в унитарном режиме.
На графике снизу показана измеренная неадиабатическая работа Q* – превышение реально совершаемой работы над идеальным адиабатическим пределом. При использовании короткого пути к адиабатичности в конце протокола она зануляется, а при наивном сжатии (коричневые точки) – нет.
#атомные_газы #квантовая_термодинамика
Интересная работа по теории обучения нейросетей, в которой обсуждается недавно открытый закон степенного скейлинга, возникающий в больших языковых моделях – таких, как GPT-3, LaMDA и Palm.
Этот закон состоит в том, что минимальная величина функции ошибок на тестовой выборке, достигаемая в ходе обучения и характеризующая эффективность работы нейросети, спадает степенным образом как функция либо числа элементов обучающей выборки T, либо числа параметров нейросети N – в зависимости от того, какая из этих величин является «бутылочным горлышком». Иллюстрация такой зависимости показана на рисунке: при росте объема обучающих данных T величина ошибки L падает степенным образом, пока не упрется в плато. А величина такого плато сама зависит от числа параметров нейросети N, степенным образом снижаясь при его увеличении.
Закон можно использовать для прогнозирования того, насколько сильно нам нужно увеличивать или объем данных, или размер сети, если мы хотим добиться улучшения качества ее работы.
#нейронные_сети
Этот закон состоит в том, что минимальная величина функции ошибок на тестовой выборке, достигаемая в ходе обучения и характеризующая эффективность работы нейросети, спадает степенным образом как функция либо числа элементов обучающей выборки T, либо числа параметров нейросети N – в зависимости от того, какая из этих величин является «бутылочным горлышком». Иллюстрация такой зависимости показана на рисунке: при росте объема обучающих данных T величина ошибки L падает степенным образом, пока не упрется в плато. А величина такого плато сама зависит от числа параметров нейросети N, степенным образом снижаясь при его увеличении.
Закон можно использовать для прогнозирования того, насколько сильно нам нужно увеличивать или объем данных, или размер сети, если мы хотим добиться улучшения качества ее работы.
#нейронные_сети
👍3
Одна из причин возникновения закона степенного скейлинга для эффективности работы нейросетей состоит в масштабно-инвариантной структуре обучающих данных.
Представим, что у нас есть массив данных – набор точек в многомерном пространстве – которые мы хотим подвергнуть анализу главных компонент, чтобы выделить в нем существенную часть. Для этого мы считаем ковариационную матрицу массива данных и смотрим на спектр ее собственных значений λ, говорящих о том, насколько сильно данные варьируются в различных направлениях многомерного пространства. Если несколько λ особенно велики, а остальные гораздо меньше, то данные располагаются приблизительно на гиперплоскости – линейной оболочке собственных векторов, отвечающей большим λ.
Оказывается, что для естественных больших данных это не так: как видно на рисунке, спектры λ для картинок CIFAR-10 и для текстов из Википедии являются степенными и не демонстрируют щелей. При росте объема выборки T протяженность этой степенной зависимости увеличивается.
#нейронные_сети
Представим, что у нас есть массив данных – набор точек в многомерном пространстве – которые мы хотим подвергнуть анализу главных компонент, чтобы выделить в нем существенную часть. Для этого мы считаем ковариационную матрицу массива данных и смотрим на спектр ее собственных значений λ, говорящих о том, насколько сильно данные варьируются в различных направлениях многомерного пространства. Если несколько λ особенно велики, а остальные гораздо меньше, то данные располагаются приблизительно на гиперплоскости – линейной оболочке собственных векторов, отвечающей большим λ.
Оказывается, что для естественных больших данных это не так: как видно на рисунке, спектры λ для картинок CIFAR-10 и для текстов из Википедии являются степенными и не демонстрируют щелей. При росте объема выборки T протяженность этой степенной зависимости увеличивается.
#нейронные_сети
🤔2
Как было описано в предыдущем посте, одна из причин возникновения закона степенного скейлинга – в том, что обучающие данные имеют масштабно-инвариантную (фрактальную) структуру. Поэтому, чем больше объем обучающих данных T, тем больше информации о них нейросеть может уловить, причем при T → ∞ предел роста эффективности обучения на больших данных не просматривается.
Откуда тогда возникает степенной скейлинг еще и по N – числу параметров нейросети? Авторы показывают, что если повторить анализ спектра собственных значений λ ковариационной матрицы, но не для исходных обучающих данных, а для данных, пропущенных через случайные нелинейные функции, то можно продлить степенной хвост спектра λ. Как показано на двух примерах на рисунке, при росте числа нелинейных функций N этот хвост продлевается все дальше.
Таким образом, пропускание данных через нелинейные функции, осуществляемое нейросетью при формировании их скрытых представлений, позволяет еще сильнее расширить их естественное разнообразие.
#нейронные_сети
Откуда тогда возникает степенной скейлинг еще и по N – числу параметров нейросети? Авторы показывают, что если повторить анализ спектра собственных значений λ ковариационной матрицы, но не для исходных обучающих данных, а для данных, пропущенных через случайные нелинейные функции, то можно продлить степенной хвост спектра λ. Как показано на двух примерах на рисунке, при росте числа нелинейных функций N этот хвост продлевается все дальше.
Таким образом, пропускание данных через нелинейные функции, осуществляемое нейросетью при формировании их скрытых представлений, позволяет еще сильнее расширить их естественное разнообразие.
#нейронные_сети
👍2
В этой теоретической работе показан удивительный результат: оказывается, движение атома гелия через углеродную нанотрубку структуры (5, 5) удовлетворяет критерию сверхтекучести Ландау – даже без всякой бозе-конденсации, для единственного атома!
Вдоль оси нанотрубки система является пространственно периодической, так что авторы рассматривают зонную структуру возможных возбуждений – фононов и плазмонов. Как показано на графике снизу, даже с учетом процессов переброса (Umklapp scattering) существует небольшая область импульсов атома гелия kᵢ (синяя полоса), в которой не находится доступных возбуждений, отвечающих рассеяниям на различные m-е векторы обратной решетки (красные линии).
Критическая скорость здесь относительно невелика – 200 м/с, что отвечает температуре 20 К. Однако даже при комнатной температуре оказывается, что плотность нормальной компоненты составляет порядка 0.1%. То есть даже при комнатной температуре атомы гелия могут проходить через нанотрубки почти без трения.
#сверхтекучесть #отвал_башки
Вдоль оси нанотрубки система является пространственно периодической, так что авторы рассматривают зонную структуру возможных возбуждений – фононов и плазмонов. Как показано на графике снизу, даже с учетом процессов переброса (Umklapp scattering) существует небольшая область импульсов атома гелия kᵢ (синяя полоса), в которой не находится доступных возбуждений, отвечающих рассеяниям на различные m-е векторы обратной решетки (красные линии).
Критическая скорость здесь относительно невелика – 200 м/с, что отвечает температуре 20 К. Однако даже при комнатной температуре оказывается, что плотность нормальной компоненты составляет порядка 0.1%. То есть даже при комнатной температуре атомы гелия могут проходить через нанотрубки почти без трения.
#сверхтекучесть #отвал_башки
👀4🤨1
Соотношение неопределенностей Робертсона-Шредингера σ(X)σ(Z) ≥ ½|<ψ|[X,Z]|ψ>|, более известное как соотношение неопределенностей Гейзенберга, говорят о невозможности одновременно точно определить две несовместимые между собой наблюдаемые величины, представленные некоммутирующими операторами X и Z.
Иногда эта несовместимость формулируется как принцип дополнительности Бора: на классическом уровне, доступном для коммуникации исследователям, мы можем описывать квантовую систему в рамках одной из двух дополнительных картин (например, пространственно-координатной и импульсно-энергетической), но не обеими одновременно.
Несмотря на свои многочисленные применения, соотношение неопределенностей Робертсона-Шредингера не очень-то годится на роль математического выражения принципа дополнительности, потому что завязано на спектры операторов наблюдаемых величин. Если мы трактуем принцип дополнительности как невозможность полного определения и передачи информации о значениях двух несовместимых величин, то здесь важны лишь вероятности, связанные с вектором состояния квантовой системы и собственными векторами операторов X и Z. А вот собственные значения операторов X и Z – это, с точки зрения теории информации, всего лишь метки, которые можно переобозначать без изменения информационного содержания. Но в соотношение неопределенностей Робертсона-Шредингера они входят, что излишне.
Еще один недостаток этого соотношения – контринтуитивное (опять-таки, с точки зрения теории информации) поведение стандартных отклонений σ(X) и σ(Z). Вот пример: допустим, что величина X в текущем состоянии системы принимает значения +1, 0, –1, каждое c вероятностями 1/3. В этом случае σ(X) = √<(X – <X>)²> = 1/√3. Если мы спроецируем нашу систему на собственный вектор |φ₀><φ₀| оператора X, отвечающий собственному значению 0 (то есть измерим наблюдаемую, отвечающую на вопрос «принимает ли X значение 0?») и получим отрицательный ответ, то после измерения величина X будет принимать уже два оставшихся значения +1 и –1 с равными вероятностями 1/2. В этом состоянии σ(X) = 1/√2 – это больше, чем предыдущее значение 1/√3.
Получается парадоксальная штука: мы провели над системой измерений, получили некоторую информацию о ее состоянии (а именно, что X ≠ 0), а стандартное отклонение σ(X) не уменьшилось, а возросло. Поэтому σ(X) не является мерой неопределенности величины X, хорошо определенной с точки зрения теории информации. А значит, и соотношение неопределенностей Робертсона-Шредингера с информационной точки зрения не особенно осмысленно.
#квантовая_механика #информация #объяснения
Иногда эта несовместимость формулируется как принцип дополнительности Бора: на классическом уровне, доступном для коммуникации исследователям, мы можем описывать квантовую систему в рамках одной из двух дополнительных картин (например, пространственно-координатной и импульсно-энергетической), но не обеими одновременно.
Несмотря на свои многочисленные применения, соотношение неопределенностей Робертсона-Шредингера не очень-то годится на роль математического выражения принципа дополнительности, потому что завязано на спектры операторов наблюдаемых величин. Если мы трактуем принцип дополнительности как невозможность полного определения и передачи информации о значениях двух несовместимых величин, то здесь важны лишь вероятности, связанные с вектором состояния квантовой системы и собственными векторами операторов X и Z. А вот собственные значения операторов X и Z – это, с точки зрения теории информации, всего лишь метки, которые можно переобозначать без изменения информационного содержания. Но в соотношение неопределенностей Робертсона-Шредингера они входят, что излишне.
Еще один недостаток этого соотношения – контринтуитивное (опять-таки, с точки зрения теории информации) поведение стандартных отклонений σ(X) и σ(Z). Вот пример: допустим, что величина X в текущем состоянии системы принимает значения +1, 0, –1, каждое c вероятностями 1/3. В этом случае σ(X) = √<(X – <X>)²> = 1/√3. Если мы спроецируем нашу систему на собственный вектор |φ₀><φ₀| оператора X, отвечающий собственному значению 0 (то есть измерим наблюдаемую, отвечающую на вопрос «принимает ли X значение 0?») и получим отрицательный ответ, то после измерения величина X будет принимать уже два оставшихся значения +1 и –1 с равными вероятностями 1/2. В этом состоянии σ(X) = 1/√2 – это больше, чем предыдущее значение 1/√3.
Получается парадоксальная штука: мы провели над системой измерений, получили некоторую информацию о ее состоянии (а именно, что X ≠ 0), а стандартное отклонение σ(X) не уменьшилось, а возросло. Поэтому σ(X) не является мерой неопределенности величины X, хорошо определенной с точки зрения теории информации. А значит, и соотношение неопределенностей Робертсона-Шредингера с информационной точки зрения не особенно осмысленно.
#квантовая_механика #информация #объяснения
Как говорилось в предыдущем посте, соотношение неопределенностей Робертсона-Шредингера не особо полезно с точки зрения теории информации. Его альтернативой являются энтропийные соотношения неопределенностей, имеющие дело не со стандартными отклонениями, а с энтропиями измеряемых величин.
Простейший вариант таких соотношений показан на рисунке: сумма энтропий Шеннона H(X) и H(Z) результатов измерений двух наблюдаемых X и Z ограничена снизу убывающей функцией log(1/c) величины c. Эта величина определяется как максимальное перекрытие |X> и |Z> (собственных векторов X и Z), то есть максимальный квадрат модуля их попарных скалярных произведений.
Если наборы собственных векторов X и Z почти совпадают, то c ≈ 1, так что log(1/c) ≈ 0, и наблюдаемые X, Z могут быть измерены одновременно с почти нулевой энтропией. Если же их направления максимально не совпадают, то log(1/c) достигает верхнего предела log(d), где d – размерность гильбертова пространства системы.
#квантовая_механика #информация #объяснения
Простейший вариант таких соотношений показан на рисунке: сумма энтропий Шеннона H(X) и H(Z) результатов измерений двух наблюдаемых X и Z ограничена снизу убывающей функцией log(1/c) величины c. Эта величина определяется как максимальное перекрытие |X> и |Z> (собственных векторов X и Z), то есть максимальный квадрат модуля их попарных скалярных произведений.
Если наборы собственных векторов X и Z почти совпадают, то c ≈ 1, так что log(1/c) ≈ 0, и наблюдаемые X, Z могут быть измерены одновременно с почти нулевой энтропией. Если же их направления максимально не совпадают, то log(1/c) достигает верхнего предела log(d), где d – размерность гильбертова пространства системы.
#квантовая_механика #информация #объяснения
Судя по списку авторов, в этой статье уже произошло квантовое запутывание с генерацией нелокальной информации.
#цитаты #квантовая_механика #информация
#цитаты #квантовая_механика #информация
Теория квантовой информации позволяет посмотреть свежим взглядом на школьную арифметику:
оказывается, 2 – это не 1 плюс 1, а 1 или 1.
Например, если Маша дает Пете 2 яблока, это означает, что Петя может взять себе и скушать только одно из этих яблок, но не оба сразу.
#цитаты #квантовая_механика #квантовые_вычисления #информация
оказывается, 2 – это не 1 плюс 1, а 1 или 1.
Например, если Маша дает Пете 2 яблока, это означает, что Петя может взять себе и скушать только одно из этих яблок, но не оба сразу.
#цитаты #квантовая_механика #квантовые_вычисления #информация
👍3
Интересная работа, в которой описывается и доказывается математически принцип дополнительности для локальной и нелокальной информации о квантовых системах. Его можно считать некоторым аналогом принципа дополнительности Бора: утверждения о том, что любую квантовую систему мы можем описывать в рамках одной из двух дополнительных картин (например, координатной и импульсной), но не двумя одновременно.
«Описывать» в данном случае подразумевает определение статистики наблюдаемых величин и дальнейшее использование полученной информации в нашей классической жизни: передача ее по классическим каналам связи от одних исследователей к другим, публикация полученных результатов, использование информации для извлечения работы, для решения вычислительных задач и т.д. Действительно, поскольку операторы координаты и импульса не коммутируют, мы не можем работать одновременно с полной совместной статистикой этих величин, а должны ограничиваться одной из них (или неким компромиссом между ними, как это делается в представлении когерентных состояний).
В этой работе показано, что, похожим образом, дополнительными – то есть взаимно несовместимыми – являются локальная и нелокальная информация об одной и той же квантовой системе, состоящей из двух или большего числа пространственно разнесенных подсистем (parties). Локальная информация – это та информация, которая может быть получена в результате набора локальных операций (унитарных преобразований над каждой подсистемой и проведения локальных измерений над ними) и классических коммуникаций (передачи сигналов по классическим каналам связи о результатах локальных измерений).
Более точно ее можно определить как I_l – число бит информации, которую можно получить в результате набора локальных операций и классических коммуникаций. Иными словами, это число получаемых чистых сепарабельных кубитов. Локальная информация имеет важный практический смысл: к примеру, ее можно использовать для того, чтобы превращать теплоту в работу, потому что при доступе к термостату с температурой T каждый бит локальной информации позволяет извлечь T ln 2 работы. Можно ввести еще такую величину, как I_cor = I_l – I_LO – разность между локальной информацией I_l и той информацией I_LO, которую мы можем получить только локальными операциями, без классических коммуникаций между подсистемами. То есть I_cor – это та локальная информация, которую мы можем извлечь из существующих корреляций между подсистемами.
Нелокальную информацию можно определить как число E_D синглетных максимально запутанных пар кубитов (|0>₁|1>₂ – |0>₁|1>₂)√2, распределенных по разным подсистемам, которые мы можем очистить, то есть получить в чистом виде в результате набора локальных операций и классических коммуникаций. Величина E_D имеет важный практический смысл: это число кубитов, которые мы можем подвергнуть квантовой телепортации, используя текущее состояние нашей системы как ресурс, который будет использован в ходе телепортации.
Авторы доказывают следующее неравенство: I_cor(P) + E_D(P) ≤ n/2, где n – полное число кубитов в системе. Неравенство говорит о том, что сумма локальной информации I_cor(P) и нелокальной информации E_D(P), получаемых в ходе одного и того же набора P локальных операций и классических коммуникаций, не может превышать универсального предела n/2. Таким образом, локальная и нелокальная информация взаимно дополнительны: в ходе любого набора операций P мы можем получить максимум локальной информации (использовав ее, например, для превращения тепла в работу), но тогда потеряем нелокальную информацию. А можем, наоборот, получить максимум нелокальной информации (потратив ее на телепортацию), но тогда потеряем локальную информацию. Одновременно получить максимум и локальной информации, и нелокальной информации невозможно.
#квантовая_механика #квантовые_вычисления #информация #отвал_башки
«Описывать» в данном случае подразумевает определение статистики наблюдаемых величин и дальнейшее использование полученной информации в нашей классической жизни: передача ее по классическим каналам связи от одних исследователей к другим, публикация полученных результатов, использование информации для извлечения работы, для решения вычислительных задач и т.д. Действительно, поскольку операторы координаты и импульса не коммутируют, мы не можем работать одновременно с полной совместной статистикой этих величин, а должны ограничиваться одной из них (или неким компромиссом между ними, как это делается в представлении когерентных состояний).
В этой работе показано, что, похожим образом, дополнительными – то есть взаимно несовместимыми – являются локальная и нелокальная информация об одной и той же квантовой системе, состоящей из двух или большего числа пространственно разнесенных подсистем (parties). Локальная информация – это та информация, которая может быть получена в результате набора локальных операций (унитарных преобразований над каждой подсистемой и проведения локальных измерений над ними) и классических коммуникаций (передачи сигналов по классическим каналам связи о результатах локальных измерений).
Более точно ее можно определить как I_l – число бит информации, которую можно получить в результате набора локальных операций и классических коммуникаций. Иными словами, это число получаемых чистых сепарабельных кубитов. Локальная информация имеет важный практический смысл: к примеру, ее можно использовать для того, чтобы превращать теплоту в работу, потому что при доступе к термостату с температурой T каждый бит локальной информации позволяет извлечь T ln 2 работы. Можно ввести еще такую величину, как I_cor = I_l – I_LO – разность между локальной информацией I_l и той информацией I_LO, которую мы можем получить только локальными операциями, без классических коммуникаций между подсистемами. То есть I_cor – это та локальная информация, которую мы можем извлечь из существующих корреляций между подсистемами.
Нелокальную информацию можно определить как число E_D синглетных максимально запутанных пар кубитов (|0>₁|1>₂ – |0>₁|1>₂)√2, распределенных по разным подсистемам, которые мы можем очистить, то есть получить в чистом виде в результате набора локальных операций и классических коммуникаций. Величина E_D имеет важный практический смысл: это число кубитов, которые мы можем подвергнуть квантовой телепортации, используя текущее состояние нашей системы как ресурс, который будет использован в ходе телепортации.
Авторы доказывают следующее неравенство: I_cor(P) + E_D(P) ≤ n/2, где n – полное число кубитов в системе. Неравенство говорит о том, что сумма локальной информации I_cor(P) и нелокальной информации E_D(P), получаемых в ходе одного и того же набора P локальных операций и классических коммуникаций, не может превышать универсального предела n/2. Таким образом, локальная и нелокальная информация взаимно дополнительны: в ходе любого набора операций P мы можем получить максимум локальной информации (использовав ее, например, для превращения тепла в работу), но тогда потеряем нелокальную информацию. А можем, наоборот, получить максимум нелокальной информации (потратив ее на телепортацию), но тогда потеряем локальную информацию. Одновременно получить максимум и локальной информации, и нелокальной информации невозможно.
#квантовая_механика #квантовые_вычисления #информация #отвал_башки
Physical Review A
Mutually exclusive aspects of information carried by physical systems: Complementarity between local and nonlocal information
Complex physical systems contain information which, under some well-defined processes can differentiate between local and nonlocal information. Both these fundamental aspects of information are defined operationally. Local information is locally accessible…
Простейший пример взаимной дополнительности локальной и нелокальной информации, описанной в предыдущем посте, возникает в случае двух максимально запутанных кубитов.
Если у нас имеется белловская пара в состоянии (|0>₁|1>₂ – |0>₁|1>₂)√2, то мы можем извлечь из нее 1 бит локальной информации. Например, Алиса измеряет состояние своего кубита и отправляет результат Бобу по классическому каналу связи, а Боб инвертирует свой кубит, если у Алисы получилось состояние |0>, и не трогает его в противном случае. Таким образом, у Боба окажется кубит, достоверно находящийся в состоянии |0>. Его можно потом использовать – например, привести в максимально смешанное состояние, превратив благодаря этому теплоту в работу.
Это пример протокола, в котором мы, в ходе набора локальных операций и классических коммуникаций, получаем 1 бит локальной информации, но полностью теряем нелокальную информацию: после пересылки результата измерения по классическому каналу связи квантовая запутанность кубитов разрушается. Но можем, напротив, использовать исходное состояние двух кубитов для извлечения нелокальной информации – а именно, для стандартной квантовой телепортации одного кубита. Можно показать, что после этого состояния двух исходных кубитов, использованных в качестве ресурса для осуществления телепортации, будут максимально смешанными, так что из них уже нельзя будет извлечь никакой локальной информации. Оба этих случая попадают под описанное выше неравенство I_cor(P) + E_D(P) ≤ n/2 = 1 для системы n = 2 кубитов. В первом случае 1 + 0 ≤ 1, во втором 0 + 1 ≤ 1.
Примечательно, что если вся совместная квантовая система находится в чистом состоянии, то это вместо этого неравенства можно записать равенство max[I_cor] + max[E_D] = I_M, где I_M – взаимная информация подсистем, а максимумы берутся по всем возможным протоколам P. В случае белловской пары кубитов I_M = 2, и это часто трактуется в таком духе, что взаимная информация складывается из «классической» части (1 бита, обусловленного скоррелированностью состояний кубитов) и существенно квантовой части (1 бита, содержащего информацию об относительной фазе двух кубитов). Указанное выше равенство 1 + 1 = 2 выражает такую трактовку на математическом уровне.
Но любопытно, что на практике, используя лишь локальные операции и классические коммуникации, мы не можем использовать оба этих бита взаимной информации одновременно. Мы извлекаем лишь первый из них (локальную информацию), либо второй (нелокальную информацию). В этом смысл утверждения авторов о том, что 2 – это не 1 + 1, а 1 или 1.
#квантовая_механика #квантовые_вычисления #информация #отвал_башки
Если у нас имеется белловская пара в состоянии (|0>₁|1>₂ – |0>₁|1>₂)√2, то мы можем извлечь из нее 1 бит локальной информации. Например, Алиса измеряет состояние своего кубита и отправляет результат Бобу по классическому каналу связи, а Боб инвертирует свой кубит, если у Алисы получилось состояние |0>, и не трогает его в противном случае. Таким образом, у Боба окажется кубит, достоверно находящийся в состоянии |0>. Его можно потом использовать – например, привести в максимально смешанное состояние, превратив благодаря этому теплоту в работу.
Это пример протокола, в котором мы, в ходе набора локальных операций и классических коммуникаций, получаем 1 бит локальной информации, но полностью теряем нелокальную информацию: после пересылки результата измерения по классическому каналу связи квантовая запутанность кубитов разрушается. Но можем, напротив, использовать исходное состояние двух кубитов для извлечения нелокальной информации – а именно, для стандартной квантовой телепортации одного кубита. Можно показать, что после этого состояния двух исходных кубитов, использованных в качестве ресурса для осуществления телепортации, будут максимально смешанными, так что из них уже нельзя будет извлечь никакой локальной информации. Оба этих случая попадают под описанное выше неравенство I_cor(P) + E_D(P) ≤ n/2 = 1 для системы n = 2 кубитов. В первом случае 1 + 0 ≤ 1, во втором 0 + 1 ≤ 1.
Примечательно, что если вся совместная квантовая система находится в чистом состоянии, то это вместо этого неравенства можно записать равенство max[I_cor] + max[E_D] = I_M, где I_M – взаимная информация подсистем, а максимумы берутся по всем возможным протоколам P. В случае белловской пары кубитов I_M = 2, и это часто трактуется в таком духе, что взаимная информация складывается из «классической» части (1 бита, обусловленного скоррелированностью состояний кубитов) и существенно квантовой части (1 бита, содержащего информацию об относительной фазе двух кубитов). Указанное выше равенство 1 + 1 = 2 выражает такую трактовку на математическом уровне.
Но любопытно, что на практике, используя лишь локальные операции и классические коммуникации, мы не можем использовать оба этих бита взаимной информации одновременно. Мы извлекаем лишь первый из них (локальную информацию), либо второй (нелокальную информацию). В этом смысл утверждения авторов о том, что 2 – это не 1 + 1, а 1 или 1.
#квантовая_механика #квантовые_вычисления #информация #отвал_башки
Physical Review A
Mutually exclusive aspects of information carried by physical systems: Complementarity between local and nonlocal information
Complex physical systems contain information which, under some well-defined processes can differentiate between local and nonlocal information. Both these fundamental aspects of information are defined operationally. Local information is locally accessible…
В некоторых материалах и диапазонах частот групповая скорость распространяющейся в ней волны оказывается отрицательной. Казалось бы, это противоречит принципу причинности: волновой пакет как целое будет распространяться не вперед, а назад, так что на выходе сигнал появится раньше, чем на входе.
В этой работе рассматривается электронный аналог подобного вещества: соединенные последовательно полосовые усилители, каждый из которых в большей части спектра дает отрицательную групповую задержку проходящего через него волнового пакета. При пропускании через такую систему волновых пакетов их «центры масс» на выходе оказываются опережающими таковые на входе, потому что передняя часть пакета усиливается сильнее задней.
Это и есть проявление отрицательной групповой скорости: как видно на графиках справа, в среднем пакет выходит из системы раньше, чем входит. Но начальный фронт сигнала появляется на выходе одновременно со входным, так что принцип причинности здесь не нарушается.
#электродинамика #объяснения
В этой работе рассматривается электронный аналог подобного вещества: соединенные последовательно полосовые усилители, каждый из которых в большей части спектра дает отрицательную групповую задержку проходящего через него волнового пакета. При пропускании через такую систему волновых пакетов их «центры масс» на выходе оказываются опережающими таковые на входе, потому что передняя часть пакета усиливается сильнее задней.
Это и есть проявление отрицательной групповой скорости: как видно на графиках справа, в среднем пакет выходит из системы раньше, чем входит. Но начальный фронт сигнала появляется на выходе одновременно со входным, так что принцип причинности здесь не нарушается.
#электродинамика #объяснения
👍2
Как мы все помним из курса оптики, вблизи частоты резонансного поглощения нормальная дисперсия, то есть растущая n(ω), сменяется аномальной, то есть убывающей n(ω), а затем снова нормальной. Это означает, что групповая скорость отрицательна вблизи резонанса, положительна вдали от него и два раза переходит через ±∞ между этими областями.
Как я писал в предыдущем посте, аномальное поведение групповой скорости не противоречит принципу причинности. Групповая скорость определяет лишь скорость распространения «центра масс» волнового пакета, а начальный фронт импульса никогда не распространяется быстрее скорости света. Если групповая скорость отрицательна, время средней задержки импульса при прохождении через вещество тоже отрицательно, если же уходит в ±∞, то время задержки зануляется.
Вот эксперимент с допированным фосфидом галлия, где хорошо видно, как ведет себя измеренная задержка импульса вблизи экситонного резонанса – ровно так, как описывается теорией.
#электродинамика #объяснения
Как я писал в предыдущем посте, аномальное поведение групповой скорости не противоречит принципу причинности. Групповая скорость определяет лишь скорость распространения «центра масс» волнового пакета, а начальный фронт импульса никогда не распространяется быстрее скорости света. Если групповая скорость отрицательна, время средней задержки импульса при прохождении через вещество тоже отрицательно, если же уходит в ±∞, то время задержки зануляется.
Вот эксперимент с допированным фосфидом галлия, где хорошо видно, как ведет себя измеренная задержка импульса вблизи экситонного резонанса – ровно так, как описывается теорией.
#электродинамика #объяснения
👍2
Еще насчет групповой скорости: ситуация, при которой она оказывается отрицательной и обеспечивает «сверхсветовой» режим распространения импульсов – не что-то атипичное и патологическое. Напротив, существование областей частот, в которой групповая скорость ведет себя аномально, неизбежно вытекает из принципа причинности.
В этой работе при помощи соотношений Крамерса-Кронига доказываются две теоремы. Согласно первой теореме, в любой среде с линейным откликом – неважно, поглощающей, активной или смешанной – должны существовать значения частот, при которых групповая скорость v_g либо превышает скорость света, либо уходит в бесконечность, либо отрицательна. Вторая теорема гласит, что при той частоте, где поглощение достигает абсолютного максимума, групповая скорость обязана быть отрицательной. Интуитивно это понятно, поскольку в пике поглощения мы имеем аномальную дисперсию.
Hа рисунке показан пример поведения групповой задержки L/v_g в материале с полосами поглощения и усиления.
#электродинамика #объяснения
В этой работе при помощи соотношений Крамерса-Кронига доказываются две теоремы. Согласно первой теореме, в любой среде с линейным откликом – неважно, поглощающей, активной или смешанной – должны существовать значения частот, при которых групповая скорость v_g либо превышает скорость света, либо уходит в бесконечность, либо отрицательна. Вторая теорема гласит, что при той частоте, где поглощение достигает абсолютного максимума, групповая скорость обязана быть отрицательной. Интуитивно это понятно, поскольку в пике поглощения мы имеем аномальную дисперсию.
Hа рисунке показан пример поведения групповой задержки L/v_g в материале с полосами поглощения и усиления.
#электродинамика #объяснения
👍2
В этой работе теоретически рассмотрен магнонный спиновый конденсатор – аналог конденсатора, в котором на обкладках вместо противоположных электрических зарядов накапливаются магноны с противоположными спинами.
Он состоит из двух ферромагнетиков, играющих роль обкладок и связанных обменным XXZ-взаимодействием между электронными спинами. Спиновые токи, поступающие на них из прилегающих электродов, накапливаются и создают разность химических потенциалов магнонов, аналогичную напряжению на конденсаторе.
Как в случае обычного конденсатора, емкость магнонного конденсатора складывается из классической и квантовой емкости. Квантовая емкость обусловлена сжимаемостью магнонного газа в каждой обкладке, а классическая – XXZ-взаимодействием обкладок (в то время как в обычном конденсаторе она обусловлена электростатическим взаимодействием). Интересно, что у магнонного конденсатора классическая емкость обратно пропорциональна площади обкладок, а еще она может быть как положительной, так и отрицательной.
#магнетизм
Он состоит из двух ферромагнетиков, играющих роль обкладок и связанных обменным XXZ-взаимодействием между электронными спинами. Спиновые токи, поступающие на них из прилегающих электродов, накапливаются и создают разность химических потенциалов магнонов, аналогичную напряжению на конденсаторе.
Как в случае обычного конденсатора, емкость магнонного конденсатора складывается из классической и квантовой емкости. Квантовая емкость обусловлена сжимаемостью магнонного газа в каждой обкладке, а классическая – XXZ-взаимодействием обкладок (в то время как в обычном конденсаторе она обусловлена электростатическим взаимодействием). Интересно, что у магнонного конденсатора классическая емкость обратно пропорциональна площади обкладок, а еще она может быть как положительной, так и отрицательной.
#магнетизм
Какой статистикой описываются величины весов w межнейронных связей в большой обученной нейронной сети? Авторы этой работы подходят к такой задаче с точки зрения экономической теории игр: число связей с одним и тем же модулем весов |w| определяется компромиссом между выгодой (минимизацей функции потерь) от существования таких связей, издержками на их поддержание и соревнованием между связями. В равновесии Нэша суммарная полезность всех величин |w| достигает максимума.
Простейшая модель для полезности и издержек показывает, что в равновесии модули |w| должны следовать логнормальному распределению – то есть логарифм ln |w| должен иметь гауссово распределение. Как показано на графиках, эмпирическая статистика весов в современных больших нейронных сетях действительно описывается логнормальным распределением.
Интересно, что такая статистика проявляется, только когда число связей действительно большое – как минимум, несколько десятков тысяч, что можно считать аналогом термодинамического предела.
#нейронные_сети
Простейшая модель для полезности и издержек показывает, что в равновесии модули |w| должны следовать логнормальному распределению – то есть логарифм ln |w| должен иметь гауссово распределение. Как показано на графиках, эмпирическая статистика весов в современных больших нейронных сетях действительно описывается логнормальным распределением.
Интересно, что такая статистика проявляется, только когда число связей действительно большое – как минимум, несколько десятков тысяч, что можно считать аналогом термодинамического предела.
#нейронные_сети