С ума сойти, у этой статьи сотрудников Google про использование долгой краткосрочной памяти для машинного перевода 23664 цитирования, набравшихся меньше чем за 10 лет.
Для сравнения:
- У эпохальной статьи Бардина, Купера и Шриффера по теории сверхпроводимости (1957 г.) всего 9265 цитирований.
- Статья Фано о резонансах Фано (1961 г.), называемая в Википедии одной из самых цитируемых работ по физике, имеет 9432 цитирования.
- Статья Хоэнберга и Кона, где сообщается об изобретении метода функционала плотности (1964 г.), имеет 38993 цитирования.
#цитаты
Для сравнения:
- У эпохальной статьи Бардина, Купера и Шриффера по теории сверхпроводимости (1957 г.) всего 9265 цитирований.
- Статья Фано о резонансах Фано (1961 г.), называемая в Википедии одной из самых цитируемых работ по физике, имеет 9432 цитирования.
- Статья Хоэнберга и Кона, где сообщается об изобретении метода функционала плотности (1964 г.), имеет 38993 цитирования.
#цитаты
👍7
В этой работе долгая краткосрочная память была использована в комбинации с механизмом внимания для обучения нейронной сети задачам понимания текстов.
От обычной архитектуры с долгой кратковременной памятью отличие здесь в том, что нейросеть сопоставляет текущее слово x(t), которое поступает ей на вход, с о всеми предыдущими выходными сигналами h(t–1), h(t–2), … и использует для расчета значений вентилей и обновления состояния памяти c(t) только те предыдущие состояния памяти и те предыдущие выходные сигналы, которые хорошо «резонируют» с текущим словом. Иными словами, при анализе каждого слова нейросеть обращает внимание на результаты обработки предшествующих слов, проводя между разными словами в предложении смысловые связи.
На рисунке показана пара примеров того, при решении задачи о том, выражает ли предложение положительное или отрицательное отношение к описываемому объекту, нейросеть в первую очередь связывает между собой важные по смыслу ключевые слова.
#нейронные_сети #популярное
От обычной архитектуры с долгой кратковременной памятью отличие здесь в том, что нейросеть сопоставляет текущее слово x(t), которое поступает ей на вход, с о всеми предыдущими выходными сигналами h(t–1), h(t–2), … и использует для расчета значений вентилей и обновления состояния памяти c(t) только те предыдущие состояния памяти и те предыдущие выходные сигналы, которые хорошо «резонируют» с текущим словом. Иными словами, при анализе каждого слова нейросеть обращает внимание на результаты обработки предшествующих слов, проводя между разными словами в предложении смысловые связи.
На рисунке показана пара примеров того, при решении задачи о том, выражает ли предложение положительное или отрицательное отношение к описываемому объекту, нейросеть в первую очередь связывает между собой важные по смыслу ключевые слова.
#нейронные_сети #популярное
Небольшой обзорчик по нанофотонике – всевозможным усилиям, направленным на то, чтобы сжать свет, имеющий длину волны порядка микрона, на размеры десятков нанометров или меньше, и при помощи этого реализовывать эффекты, невозможные в традиционной оптике.
Сжатие света можно осуществлять при помощи дефектов или щелей в фотонных кристаллах (A), металлических пластин (B) или наночастиц (C). При сжатии электрическое поле света усиливается на порядки, так что можно усиливать его взаимодействие с веществом. К примеру, в экспериментах достигнуто более чем 1000-кратное усиление поглощения и испускания фотонов молекулами, расположенными вблизи наночастиц.
Еще одна возможность, открываемая манипуляциями светом на наномасштабах – это создание эффективного магнитного отклика на основе чисто электрического при помощи киральных металлических структур (D). Отдельно интересны метаповерхности (E): они дают возможность манипулировать светом и при этом слабо его поглощают благодаря малой толщине.
#фотоника #электродинамика
Сжатие света можно осуществлять при помощи дефектов или щелей в фотонных кристаллах (A), металлических пластин (B) или наночастиц (C). При сжатии электрическое поле света усиливается на порядки, так что можно усиливать его взаимодействие с веществом. К примеру, в экспериментах достигнуто более чем 1000-кратное усиление поглощения и испускания фотонов молекулами, расположенными вблизи наночастиц.
Еще одна возможность, открываемая манипуляциями светом на наномасштабах – это создание эффективного магнитного отклика на основе чисто электрического при помощи киральных металлических структур (D). Отдельно интересны метаповерхности (E): они дают возможность манипулировать светом и при этом слабо его поглощают благодаря малой толщине.
#фотоника #электродинамика
Интересный эксперимент, где на примере одномерного атомного газа было продемонстрировано, что в квантовой многочастичной системе термализация – установление теплового равновесия – распространяется в пространстве с конечной скоростью.
Вытянутый в нить бозе-конденсированный газ атомов рубидия аккуратно расщеплялся на две параллельные нити, квантовые состояния которых с течением времени начинают расходиться из-за хаотичности идущей в них термализации.
Интерференционными измерениями можно отслеживать, как с течением времени спадает корреляционная функция C = Re<exp{iφ(z,t) – iφ(z′,t)}> относительной фазы φ = θ₁ – θ₂ двух конденсатов.
Как видно на рисунке, ростом расстояния z – z′ она спадает экспоненциально до какого-то предельного расстояния d, после чего выходит на константу. А само это предельное расстояние d = 2ct линейно растет с течением времени t, прошедшего после разделения нитей, с удвоенной характерной скоростью возбуждений c, образующихся в ходе термализации.
#атомные_газы #квантовая_термодинамика
Вытянутый в нить бозе-конденсированный газ атомов рубидия аккуратно расщеплялся на две параллельные нити, квантовые состояния которых с течением времени начинают расходиться из-за хаотичности идущей в них термализации.
Интерференционными измерениями можно отслеживать, как с течением времени спадает корреляционная функция C = Re<exp{iφ(z,t) – iφ(z′,t)}> относительной фазы φ = θ₁ – θ₂ двух конденсатов.
Как видно на рисунке, ростом расстояния z – z′ она спадает экспоненциально до какого-то предельного расстояния d, после чего выходит на константу. А само это предельное расстояние d = 2ct линейно растет с течением времени t, прошедшего после разделения нитей, с удвоенной характерной скоростью возбуждений c, образующихся в ходе термализации.
#атомные_газы #квантовая_термодинамика
В этом эксперименте обнаружена спонтанная генерация циркулирующих токов экситон-поляритонного бозе-конденсата при нерезонансной накачке.
Луч накачки имеет форму кольца, которое для бозе-конденсата служит источником новых поляритонов и одновременно отталкивающим потенциалом. Как показано на первой строке диаграмм для амплитуды и фазы люминесцентного излучения, фазовый профиль образовавшегося облака конденсата внутри кольца имеет странный вид со скачком фазы на величину π вдоль диаметра. Но амплитуда конденсата в этом месте не проваливается до нуля (как должно быть на топологическом дефекте). Как считают авторы, это свидетельствует о том, что наблюдаемый скачок фазы – это результат усреднения токов, случайно меняющих свое направление.
Если добавить к лучу накачки еще один небольшой лазерный луч сбоку, то круговая симметрия системы нарушается, давая начало спонтанно вращающемуся конденсату: либо по часовой стрелке (вторая строка диаграмм), либо против часовой (третья строка).
#поляритоны #бозе_конденсация
Луч накачки имеет форму кольца, которое для бозе-конденсата служит источником новых поляритонов и одновременно отталкивающим потенциалом. Как показано на первой строке диаграмм для амплитуды и фазы люминесцентного излучения, фазовый профиль образовавшегося облака конденсата внутри кольца имеет странный вид со скачком фазы на величину π вдоль диаметра. Но амплитуда конденсата в этом месте не проваливается до нуля (как должно быть на топологическом дефекте). Как считают авторы, это свидетельствует о том, что наблюдаемый скачок фазы – это результат усреднения токов, случайно меняющих свое направление.
Если добавить к лучу накачки еще один небольшой лазерный луч сбоку, то круговая симметрия системы нарушается, давая начало спонтанно вращающемуся конденсату: либо по часовой стрелке (вторая строка диаграмм), либо против часовой (третья строка).
#поляритоны #бозе_конденсация
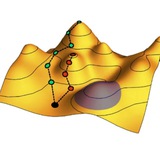
Познавательная статья с небольшим обзором о связи между NP-трудными вычислительными задачами и теорией спиновых стекол, а также теорией обучения нейронных сетей.
Действительно, задачи комбинаторной оптимизации – например, задача коммивояжера, поиск максимальной клики или максимального разреза графа – сводятся к поиску глобального минимума функции ошибок в некотором многомерном пространстве. Математически это эквивалентно поиску основного состояния спинового стекла – большого числа классических спинов, соединенных случайными ферро- и антиферромагнитными взаимодействиями. Задача обучения нейросети – тоже поиск минимума функции ошибок в пространстве ее параметров.
Как и в случае спинового стекла, в задачах оптимизации существует фазовый переход между «упорядоченным» состоянием, где поиск глобального минимума сравнительно прост, и «аморфной» (или трудной) фазой, где потенциальный ландшафт становится сильно изрезанным с большим числом локальных минимумов, разделенных высокими барьерами.
#стекла #оптимизация
Действительно, задачи комбинаторной оптимизации – например, задача коммивояжера, поиск максимальной клики или максимального разреза графа – сводятся к поиску глобального минимума функции ошибок в некотором многомерном пространстве. Математически это эквивалентно поиску основного состояния спинового стекла – большого числа классических спинов, соединенных случайными ферро- и антиферромагнитными взаимодействиями. Задача обучения нейросети – тоже поиск минимума функции ошибок в пространстве ее параметров.
Как и в случае спинового стекла, в задачах оптимизации существует фазовый переход между «упорядоченным» состоянием, где поиск глобального минимума сравнительно прост, и «аморфной» (или трудной) фазой, где потенциальный ландшафт становится сильно изрезанным с большим числом локальных минимумов, разделенных высокими барьерами.
#стекла #оптимизация
👍2
А в этой работе обсуждается щель между перекрытиями (overlap gap) – свойство трудных оптимизационных задач, налагающее фундаментальные ограничения на эффективность многих направленных на их решение эвристических алгоритмов.
Это свойство заключается в следующим: рассмотрим функцию потерь трудной оптимизационной задачи L(σ) σ. Конфигурации, для которых L(σ) ≤ L* + μ, где L* – типичное положение глобального минимума функции потерь на множестве случайных примеров задач данного класса, μ > 0, можно назвать μ-оптимальными, то есть они не хуже «наилучшей» лишь на величину μ. Тогда расстояние d(σ, ξ) между любыми двумя μ-оптимальными конфигурациями σ и ξ, должно быть либо меньше ν₁, либо больше ν₂, где ν₂ > ν₁.
Графически это свойство показано на рисунке: оно говорит о том, что близкие к оптимуму конфигурации разбиваются на кластеры: любые две из них либо близки и попадают в один кластер (когда d(σ, ξ) < ν₁), либо далеки и попадают в разные кластеры (d(σ, ξ) > ν₂).
#стекла #оптимизация
Это свойство заключается в следующим: рассмотрим функцию потерь трудной оптимизационной задачи L(σ) σ. Конфигурации, для которых L(σ) ≤ L* + μ, где L* – типичное положение глобального минимума функции потерь на множестве случайных примеров задач данного класса, μ > 0, можно назвать μ-оптимальными, то есть они не хуже «наилучшей» лишь на величину μ. Тогда расстояние d(σ, ξ) между любыми двумя μ-оптимальными конфигурациями σ и ξ, должно быть либо меньше ν₁, либо больше ν₂, где ν₂ > ν₁.
Графически это свойство показано на рисунке: оно говорит о том, что близкие к оптимуму конфигурации разбиваются на кластеры: любые две из них либо близки и попадают в один кластер (когда d(σ, ξ) < ν₁), либо далеки и попадают в разные кластеры (d(σ, ξ) > ν₂).
#стекла #оптимизация
Щель между перекрытиями, о которой говорилось в предыдущем посте, налагает ограничения на эффективность быстрых эвристических алгоритмов, призванных решать трудные оптимизационные задачи.
Действительно, многие быстрые алгоритмы полиномиальной трудоемкости являются стабильными: то есть даваемые ими решения задачи слабо меняются при слабых изменениях условии задачи (например, при удалении единственного ребра большого графа, в котором нужно найти максимальную клику). Кластеризация же решений задачи, вытекающая из существования щели между перекрытиями, говорит о том, что не только наилучшее (тот самый единственный глобальный минимум функции потерь), но и близкие к наилучшему решения могут резко и непредсказуемо меняться при изменении условий задачи. Быстрый эвристический алгоритм, попадающий в кластер почти оптимальных решений и потому дающий хороший результат на одном экземпляре задачи, может дать куда худший результат при слегка измененных условиях задачи – потому что этот кластер может уже стать сильно неоптимальным.
С этим свойством, вероятно, связано и наблюдающийся в некоторых оптимизационных задачах существенный разрыв между типичным и алгоритмическим оптимумами. Что это такое, можно понять на примере задачи поиска максимальной клики (подмножества узлов, которые все попарно соединены между собой) в случайном графе Эрдёша-Реньи, где любые два узла соединены или не соединены ребром с вероятностью 1/2. Известно, что при общем числе узлов N >> 1 типичный размер максимальной клики в таком графе должен быть порядка 2log₂N. Это доказывается неконструктивным образом, то есть доказательство этого факта показывает, что клика такого размера с вероятностью, стремящейся к 1, должна существовать в достаточно большом графе, но не показывает, как эту клику найти. В то же время, типичный полиномиально быстрый алгоритм – например, алгоритм Карпа – находит клику лишь с максимальным размером порядка log₂N.
Как видно, существует разрыв между типичным оптимумом log₂N, даваемым быстрым алгоритмом, и типичным глобальным оптимумом задачи 2log₂N, причем этот разрыв существенен: с ростом размера задачи N он лишь увеличивается. Это свидетельствует о том, что быстрый алгоритм, как правило, ведет нас отнюдь не в те области конфигурационного пространства, где находятся близкие к оптимальному решения.
#стекла #оптимизация
Действительно, многие быстрые алгоритмы полиномиальной трудоемкости являются стабильными: то есть даваемые ими решения задачи слабо меняются при слабых изменениях условии задачи (например, при удалении единственного ребра большого графа, в котором нужно найти максимальную клику). Кластеризация же решений задачи, вытекающая из существования щели между перекрытиями, говорит о том, что не только наилучшее (тот самый единственный глобальный минимум функции потерь), но и близкие к наилучшему решения могут резко и непредсказуемо меняться при изменении условий задачи. Быстрый эвристический алгоритм, попадающий в кластер почти оптимальных решений и потому дающий хороший результат на одном экземпляре задачи, может дать куда худший результат при слегка измененных условиях задачи – потому что этот кластер может уже стать сильно неоптимальным.
С этим свойством, вероятно, связано и наблюдающийся в некоторых оптимизационных задачах существенный разрыв между типичным и алгоритмическим оптимумами. Что это такое, можно понять на примере задачи поиска максимальной клики (подмножества узлов, которые все попарно соединены между собой) в случайном графе Эрдёша-Реньи, где любые два узла соединены или не соединены ребром с вероятностью 1/2. Известно, что при общем числе узлов N >> 1 типичный размер максимальной клики в таком графе должен быть порядка 2log₂N. Это доказывается неконструктивным образом, то есть доказательство этого факта показывает, что клика такого размера с вероятностью, стремящейся к 1, должна существовать в достаточно большом графе, но не показывает, как эту клику найти. В то же время, типичный полиномиально быстрый алгоритм – например, алгоритм Карпа – находит клику лишь с максимальным размером порядка log₂N.
Как видно, существует разрыв между типичным оптимумом log₂N, даваемым быстрым алгоритмом, и типичным глобальным оптимумом задачи 2log₂N, причем этот разрыв существенен: с ростом размера задачи N он лишь увеличивается. Это свидетельствует о том, что быстрый алгоритм, как правило, ведет нас отнюдь не в те области конфигурационного пространства, где находятся близкие к оптимальному решения.
#стекла #оптимизация
PNAS
The overlap gap property: A topological barrier to optimizing over random structures | Proceedings of the National Academy of Sciences
The problem of optimizing over random structures emerges in many areas of science
and engineering, ranging from statistical physics to machine lear...
and engineering, ranging from statistical physics to machine lear...
Очень интересная работа, в которой предлагается новый взгляд на закон Ципфа, позволяющий не только понять механизмы его формирования, но и делать важные практические выводы. Например, при помощи анализа статистики можно понять – произошло ли уже самое крупное из возможных землетрясений в определенной местности, или оно еще предстоит в будущем?
Как я писал подробнее раньше, закон Ципфа, определяющий степенную зависимость размеров объектов s (населенностей городов, чисел просмотров веб-страниц, частот встречаемости слов в тексте и т.д.) от их ранга k, или номера по убыванию размера, часто выполняется в виде обобщенного закона Ципфа-Мандельброта s ~ 1/(k + Q)ᵞ. Параметр Q > 0 служит мерой отклонения наблюдаемой статистики от «настоящего» степенного закона Ципфа s ~ 1/kᵞ. С математической точки зрения, он не дает размерам s самых крупных объектов (k = 1,2,3,…) расти слишком быстро и устанавливает верхний предел размеров s_max.
Авторы работы предлагают посмотреть на то, как параметр Q меняется в динамике, по мере постепенного расширения статистики. Например, размеры городов в США в 1790-м году описывались законом Ципфа-Мандельброта с Q = 5.2, а в 1900-м году – уже с Q = 0.3, то есть с течением времени статистика становится все более ципфовской. Напротив, для землетрясений в Италии, случившихся с 1950-го по 2000-й годы, Q = 0, а для более обширной статистики землетрясений с 1000-го по 2000-й годы Q = 7.1. Получается, что статистика землетрясений в Италии, по мере включения в нее все большего числа данных с более широких промежутков времени, становится все менее ципфовской.
О чем свидетельствует уменьшение либо увеличение параметра Q в динамике? Как говорилось выше, он устанавливает верхний предел s_max для размеров объектов, которые будут встречаться нам на практике в заданный временной период. И если Q постепенно растет, это значит, что изучаемая система уже достигла максимального предела размера объектов s_max, которые она способна произвести. По мере включения в статистику новых объектов (появления новых городов, возникновения новых землетрясений и т.д.) их размеры s не будут превышать s_max, что будет приводить к росту Q, как можно показать при помощи масштабного анализа распределения. Напротив, если Q постепенно уменьшается, стремясь к нулю, это означает, что система воспроизводит все более крупные объекты, постепенно сдвигая максимальный размер s_max вверх.
Это ключевой момент работы: анализ закона Ципфа в динамике – а именно, анализ поведения параметра Q – позволяет понять, «выдохлась» ли изучаемая система, уже продемонстрировав нам максимальные по размерам объекты, или же она еще может нас удивить новыми рекордами. То, что происходит во втором случае, называется словом undersampling: наблюдаемая выборка объектов разных размеров (их вероятностная генерация называется словом sampling) еще слишком мала и не дает представления обо всем диапазоне размеров, от минимального до максимального. Иными словами, размер выборки в динамике растет медленнее размера вероятностного пространства.
Динамический анализ закона Ципфа позволяет делать важные выводы. Например, увеличение Q для статистики землетрясений в Италии говорит о том, что самое крупное землетрясение в этом регионе, вероятно, уже произошло. И те землетрясения, которые возможны в будущем, весьма вероятно, не будут превышать по масштабу уже случившиеся. А вот размеры городов в США еще не дошли до максимума: в будущем они будут еще расти, потому что параметр Q для них с течением времени уменьшается.
В принципе, можно применять такой анализ и к другого рода событиям: например, можно попытаться ответить на вопрос, столкнется ли человечество в будущем с войной еще большего масштаба, чем Вторая мировая, или настолько масштабной резни уже никогда не будет? Возможно, подобный анализ похож на гадание, но если закон Ципфа действительно улавливает в обобщенном виде закономерности поведения сложных самоорганизующихся систем, механизмы которых мы еще не до конца понимаем, то и его анализ позволит делать реальные прогнозы.
#популярное #отвал_башки #самоорганизация #общество
Как я писал подробнее раньше, закон Ципфа, определяющий степенную зависимость размеров объектов s (населенностей городов, чисел просмотров веб-страниц, частот встречаемости слов в тексте и т.д.) от их ранга k, или номера по убыванию размера, часто выполняется в виде обобщенного закона Ципфа-Мандельброта s ~ 1/(k + Q)ᵞ. Параметр Q > 0 служит мерой отклонения наблюдаемой статистики от «настоящего» степенного закона Ципфа s ~ 1/kᵞ. С математической точки зрения, он не дает размерам s самых крупных объектов (k = 1,2,3,…) расти слишком быстро и устанавливает верхний предел размеров s_max.
Авторы работы предлагают посмотреть на то, как параметр Q меняется в динамике, по мере постепенного расширения статистики. Например, размеры городов в США в 1790-м году описывались законом Ципфа-Мандельброта с Q = 5.2, а в 1900-м году – уже с Q = 0.3, то есть с течением времени статистика становится все более ципфовской. Напротив, для землетрясений в Италии, случившихся с 1950-го по 2000-й годы, Q = 0, а для более обширной статистики землетрясений с 1000-го по 2000-й годы Q = 7.1. Получается, что статистика землетрясений в Италии, по мере включения в нее все большего числа данных с более широких промежутков времени, становится все менее ципфовской.
О чем свидетельствует уменьшение либо увеличение параметра Q в динамике? Как говорилось выше, он устанавливает верхний предел s_max для размеров объектов, которые будут встречаться нам на практике в заданный временной период. И если Q постепенно растет, это значит, что изучаемая система уже достигла максимального предела размера объектов s_max, которые она способна произвести. По мере включения в статистику новых объектов (появления новых городов, возникновения новых землетрясений и т.д.) их размеры s не будут превышать s_max, что будет приводить к росту Q, как можно показать при помощи масштабного анализа распределения. Напротив, если Q постепенно уменьшается, стремясь к нулю, это означает, что система воспроизводит все более крупные объекты, постепенно сдвигая максимальный размер s_max вверх.
Это ключевой момент работы: анализ закона Ципфа в динамике – а именно, анализ поведения параметра Q – позволяет понять, «выдохлась» ли изучаемая система, уже продемонстрировав нам максимальные по размерам объекты, или же она еще может нас удивить новыми рекордами. То, что происходит во втором случае, называется словом undersampling: наблюдаемая выборка объектов разных размеров (их вероятностная генерация называется словом sampling) еще слишком мала и не дает представления обо всем диапазоне размеров, от минимального до максимального. Иными словами, размер выборки в динамике растет медленнее размера вероятностного пространства.
Динамический анализ закона Ципфа позволяет делать важные выводы. Например, увеличение Q для статистики землетрясений в Италии говорит о том, что самое крупное землетрясение в этом регионе, вероятно, уже произошло. И те землетрясения, которые возможны в будущем, весьма вероятно, не будут превышать по масштабу уже случившиеся. А вот размеры городов в США еще не дошли до максимума: в будущем они будут еще расти, потому что параметр Q для них с течением времени уменьшается.
В принципе, можно применять такой анализ и к другого рода событиям: например, можно попытаться ответить на вопрос, столкнется ли человечество в будущем с войной еще большего масштаба, чем Вторая мировая, или настолько масштабной резни уже никогда не будет? Возможно, подобный анализ похож на гадание, но если закон Ципфа действительно улавливает в обобщенном виде закономерности поведения сложных самоорганизующихся систем, механизмы которых мы еще не до конца понимаем, то и его анализ позволит делать реальные прогнозы.
#популярное #отвал_башки #самоорганизация #общество
Physical Review Research
Dynamical approach to Zipf's law
The authors show that Zipf's law can be understood only by a dynamical approach and that deviations from Zipf's law unveil physical properties of systems.
👍4❤3
А вот пара иллюстраций из статьи о динамическом анализе закона Ципфа.
На верхних графиках показана статистика магнитуд землетрясений в Италии, статистика частот встречаемости слов в романе «Моби Дик» и статистика населенностей городов в США. Верхняя строка графиков показывает их подгон под закон Ципфа-Мандельброта s ~ 1/(k + Q)ᵞ с меньшей выборкой, а нижняя – с большим размером выборки (с более широкой статистикой). В случае «идеального» закона Ципфа s ~ 1/kᵞ на графиках должна быть прямая, а параметр Q загибает ее при больших размерах s и небольших рангах k.
По тому, растет ли параметр Q или убывает, можно сделать, исчерпала ли система свою ципфовскую статистику или еще нет. А график снизу показывает, как параметр Q меняется для разных систем – как реально наблюдаемых, так и модельных. Можно видеть, какие из них уже достигли пределов роста размеров Q, а какие еще продолжают ставить рекорды, постепенно приближаясь к идеальному закону Ципфа.
#популярное #отвал_башки #самоорганизация #общество
На верхних графиках показана статистика магнитуд землетрясений в Италии, статистика частот встречаемости слов в романе «Моби Дик» и статистика населенностей городов в США. Верхняя строка графиков показывает их подгон под закон Ципфа-Мандельброта s ~ 1/(k + Q)ᵞ с меньшей выборкой, а нижняя – с большим размером выборки (с более широкой статистикой). В случае «идеального» закона Ципфа s ~ 1/kᵞ на графиках должна быть прямая, а параметр Q загибает ее при больших размерах s и небольших рангах k.
По тому, растет ли параметр Q или убывает, можно сделать, исчерпала ли система свою ципфовскую статистику или еще нет. А график снизу показывает, как параметр Q меняется для разных систем – как реально наблюдаемых, так и модельных. Можно видеть, какие из них уже достигли пределов роста размеров Q, а какие еще продолжают ставить рекорды, постепенно приближаясь к идеальному закону Ципфа.
#популярное #отвал_башки #самоорганизация #общество
И еще пара интересных примеров, позволяющих сделать практические выводы из анализа закона Ципфа.
Статистика магнитуд землетрясений в Калифорнии за 1769-2000 годы описываются законом Ципфа-Мандельброта с довольно большим Q = 9, в то время как за промежуток времени 1930-1990 годов статистика почти идеально ципфовская с Q ≈ 0 (этот случай на рисунке не показан). Отсюда можно сделать вывод, что самое сильное землетрясение в Калифорнии, вероятно, уже произошло, и в будущем не нужно ожидать землетрясений более крупных, чем с магнитудой 7.9, в которую упирается график при минимальном ранге k = 1.
А вот статистика размеров цунами (высот поднимающейся волны) совсем другая: за максимально широкий, доступный для анализа, период с древних времен до сегодняшнего времени она все еще идеально степенная с Q ≈ 0. Это означает, что в будущем нужно готовиться к цунами еще более крупным, чем уже случившиеся.
#популярное #отвал_башки #самоорганизация #общество
Статистика магнитуд землетрясений в Калифорнии за 1769-2000 годы описываются законом Ципфа-Мандельброта с довольно большим Q = 9, в то время как за промежуток времени 1930-1990 годов статистика почти идеально ципфовская с Q ≈ 0 (этот случай на рисунке не показан). Отсюда можно сделать вывод, что самое сильное землетрясение в Калифорнии, вероятно, уже произошло, и в будущем не нужно ожидать землетрясений более крупных, чем с магнитудой 7.9, в которую упирается график при минимальном ранге k = 1.
А вот статистика размеров цунами (высот поднимающейся волны) совсем другая: за максимально широкий, доступный для анализа, период с древних времен до сегодняшнего времени она все еще идеально степенная с Q ≈ 0. Это означает, что в будущем нужно готовиться к цунами еще более крупным, чем уже случившиеся.
#популярное #отвал_башки #самоорганизация #общество
😱2🤯1
Еще одно интересное обстоятельство, связанное с законом Ципфа, состоит в том, что этот закон неаддитивен. А именно, если у нас имеются две выборки объектов, каждая из которых подчиняется закону Ципфа, то объединенная выборка уже не обязательно будет им описываться.
К примеру, населенности городов в США подчиняются закону Ципфа, как уже говорилось выше. А вот статистика населенности городов по всему миру этому закону уже не подчиняется. На графике показано, как растет параметр Q по мере включения в статистику все новых городов как функция суммарного населения n, и рост Q свидетельствует о существенно неципфовской статистике.
Это означает, что города в США еще не достигли пределов роста своего размера, а города по всему миру этого предела уже достигли. Экстраполяция данных показывает, что предел населения одного города составляет около 41 млн. человек, что близко к текущему населению городской агломерации Токио, составляющей примерно 37 млн. человек.
#популярное #самоорганизация #общество
К примеру, населенности городов в США подчиняются закону Ципфа, как уже говорилось выше. А вот статистика населенности городов по всему миру этому закону уже не подчиняется. На графике показано, как растет параметр Q по мере включения в статистику все новых городов как функция суммарного населения n, и рост Q свидетельствует о существенно неципфовской статистике.
Это означает, что города в США еще не достигли пределов роста своего размера, а города по всему миру этого предела уже достигли. Экстраполяция данных показывает, что предел населения одного города составляет около 41 млн. человек, что близко к текущему населению городской агломерации Токио, составляющей примерно 37 млн. человек.
#популярное #самоорганизация #общество
Материалы с близкой к нулю диэлектрической проницаемостью ε (epsilon-near-zero-, или ENZ-материалы) обладают необычными оптическими свойствами: длина волны в них становится близкой к бесконечности, а значит, и фаза волны «растекается» по материалу однородно. Как следствие, помещенные а такой материал объекты становятся почти невидимыми, поскольку свет обтекает их, не меняя фазу волны.
Этот эксперимент подтверждает теоретические ожидания. Сверху показан двухщелевой эксперимент двумерной оптики, в котором между металлическими слоями помещен тонкий слой SiO₂. По мере увеличения свободной длины волны света λ наблюдаемые на выходе интерференционные линии становятся реже и шире, и в пределе λ = 1.29 мкм, где ε(SiO₂) ≈ 0, они уширяются до бесконечности.
Снизу показан эксперимент с обтеканием препятствия: по мере увеличения λ, наблюдаемая на выходе тень от препятствия сначала сменятся пятном Пуассона, а затем исчезает. Таким образом, при ε ≈ 0 свет игнорирует препятствие.
#фотоника #электродинамика
Этот эксперимент подтверждает теоретические ожидания. Сверху показан двухщелевой эксперимент двумерной оптики, в котором между металлическими слоями помещен тонкий слой SiO₂. По мере увеличения свободной длины волны света λ наблюдаемые на выходе интерференционные линии становятся реже и шире, и в пределе λ = 1.29 мкм, где ε(SiO₂) ≈ 0, они уширяются до бесконечности.
Снизу показан эксперимент с обтеканием препятствия: по мере увеличения λ, наблюдаемая на выходе тень от препятствия сначала сменятся пятном Пуассона, а затем исчезает. Таким образом, при ε ≈ 0 свет игнорирует препятствие.
#фотоника #электродинамика
👍3
Как мы знаем, дифракция в дальнем поле дает картину пространственного фурье-образа изучаемого объекта. Этот же принцип, в целом, работает и для дифракции электронов на кристаллах: электроны, рассеиваясь на периодическом электростатическом потенциале, дают фурье-образ в виде дискретных рефлексов, отвечающих изменениям электронного волнового вектора на векторы обратной решетки.
Но это справедливо только если электроны претерпевают преимущественно однократное рассеяние – такое приближение называется кинематической теорией дифракции. Для плотных и относительно толстых мишеней нужно пользоваться динамической теорией дифракции, учитывая многократное рассеяние электронов, – или, фактически, решая уравнение Шредингера для распространяющейся в потенциале кристалла электронной волны.
В этой работе демонстрируется, как динамическая теория дифракции согласуется с экспериментами по электронной дифракции на монокристаллах золота на порядок лучше (отклонение 2.1%), чем кинематическая (с отклонением 21%).
#твердое_тело
Но это справедливо только если электроны претерпевают преимущественно однократное рассеяние – такое приближение называется кинематической теорией дифракции. Для плотных и относительно толстых мишеней нужно пользоваться динамической теорией дифракции, учитывая многократное рассеяние электронов, – или, фактически, решая уравнение Шредингера для распространяющейся в потенциале кристалла электронной волны.
В этой работе демонстрируется, как динамическая теория дифракции согласуется с экспериментами по электронной дифракции на монокристаллах золота на порядок лучше (отклонение 2.1%), чем кинематическая (с отклонением 21%).
#твердое_тело
👍3
Динамика спина описывается дифференциальными уравнениями первого порядка (для скорости), в отличие от уравнений второго порядка (для ускорения), описывающих движение массивных тел. Это значит, что спин не имеет инерции.
Тем не менее, многие эксперименты по спиновой динамике показывают, что она демонстрирует эффективную инерцию, происхождение которой приписывается взаимодействию спина с окружением. Авторы этой теоретической работы рассмотрели макроскопически большой спин, взаимодействующий с термостатом Кальдейры-Леггетта (набором независимых осцилляторов) и вывели для него квазиклассические уравнения движения.
В результате им удалось показать, что появление инерции у спина – это универсальное явление, обусловленное высокочастотной асимптотикой его взаимодействия с термостатом (точнее, спектральной плотности термостата, показанной на рисунке). Низкочастотная же – линейная по частоте – асимптотика спектральной плотности (зеленая линия) дает затухание Гильберта.
#твердое_тело #открытые_квантовые_системы
Тем не менее, многие эксперименты по спиновой динамике показывают, что она демонстрирует эффективную инерцию, происхождение которой приписывается взаимодействию спина с окружением. Авторы этой теоретической работы рассмотрели макроскопически большой спин, взаимодействующий с термостатом Кальдейры-Леггетта (набором независимых осцилляторов) и вывели для него квазиклассические уравнения движения.
В результате им удалось показать, что появление инерции у спина – это универсальное явление, обусловленное высокочастотной асимптотикой его взаимодействия с термостатом (точнее, спектральной плотности термостата, показанной на рисунке). Низкочастотная же – линейная по частоте – асимптотика спектральной плотности (зеленая линия) дает затухание Гильберта.
#твердое_тело #открытые_квантовые_системы
👍2❤1
В этой работе сотрудников OpenAI описывается довольно сложно устроенная нейросеть, генерирующая изображения при помощи метода обратной диффузии, направляемой на основе высокоуровневой информации о каком-то уже существующем изображении (она называется здесь CLIP embedding) в комбинации (если нужно) с текстовым описанием.
Помимо обычной генерации изображений по текстовому описанию, она может решать и другие задачи:
▪️ Высокоуровневое варьирование заданного изображения.
▪️ Плавная интерполяция между двумя изображениями.
▪️ Плавное изменение заданного изображения в сторону заданного текстового описания.
На рисунке показаны примеры интерполяции между парами изображений, причем для каждой интерполяция можно создавать бесконечное число вариантов. Интерполяция проводится в пространстве скрытого представления изображения, содержащего иерархически структурированную информацию о его содержании и стиле, поэтому и сами изображения плавно меняются и по общей структуре, и по мелким деталям.
#нейронные_сети #популярное
Помимо обычной генерации изображений по текстовому описанию, она может решать и другие задачи:
▪️ Высокоуровневое варьирование заданного изображения.
▪️ Плавная интерполяция между двумя изображениями.
▪️ Плавное изменение заданного изображения в сторону заданного текстового описания.
На рисунке показаны примеры интерполяции между парами изображений, причем для каждой интерполяция можно создавать бесконечное число вариантов. Интерполяция проводится в пространстве скрытого представления изображения, содержащего иерархически структурированную информацию о его содержании и стиле, поэтому и сами изображения плавно меняются и по общей структуре, и по мелким деталям.
#нейронные_сети #популярное
Типографическая атака.png
3.3 MB
На этом рисунке иллюстрируется, как нейросеть из статьи из предыдущего поста справляется с так называемыми типографическими атаками – попытками запутать нейросеть, распознающую изображение или производящую его варьирование, поместив на фоне изображения одного объекта надпись с названием чего-то другого.
Здесь нейросети предъявляются изображения, показанные сверху, и дается задание сгенерировать их слегка измененные варианты. Результаты такой генерации показаны снизу: в большинстве случаев нейросеть оказывается устойчивой к типографическим атакам, рисуя именно яблоко с надписями “iPod” и “pizza” (или чем-то похожим), а не сами айпод или пиццу.
Что парадоксально, та часть нейросети, которая распознает исходное изображения, генерируя его структурированное скрытое представление, в случае второй картинки определяет его как айпод, а не яблоко сорта “Granny Smith” – но все равно создает потом варианты картины с яблоком.
#нейронные_сети #популярное
Здесь нейросети предъявляются изображения, показанные сверху, и дается задание сгенерировать их слегка измененные варианты. Результаты такой генерации показаны снизу: в большинстве случаев нейросеть оказывается устойчивой к типографическим атакам, рисуя именно яблоко с надписями “iPod” и “pizza” (или чем-то похожим), а не сами айпод или пиццу.
Что парадоксально, та часть нейросети, которая распознает исходное изображения, генерируя его структурированное скрытое представление, в случае второй картинки определяет его как айпод, а не яблоко сорта “Granny Smith” – но все равно создает потом варианты картины с яблоком.
#нейронные_сети #популярное
❤1
image_2023-10-11_14-28-45.png
2.5 MB
А вот еще любопытный пример: нейросети предъявляются изображения, показанные справа, и дается задание сгенерировать что-то похожее на них. При этом исходное изображение нейросеть сначала превращает в структурированное представление, называемое CLIP embedding, на основе которого производится генерация нового изображения.
Здесь авторы обрезают 2048-мерный вектор этого представления, беря только 20, 30, 40, 80, 120, 160, 200 и 320 самых значащих его компонент (которые определяются методом анализа главных компонент). Сгенерированные изображения, показанные слева направо, воспроизводят все больше деталей оригинала по мере того, как мы увеличиваем количество учитываемых компонент структурированного представления.
К примеру, в верхней строке картинок сначала воспроизводится базовая информация о том, что на изображении должны быть хоть какая-то еда и тарелка, а на поздних стадиях появляется уже информация о бутылке и деревянном столе внизу.
#нейронные_сети #популярное
Здесь авторы обрезают 2048-мерный вектор этого представления, беря только 20, 30, 40, 80, 120, 160, 200 и 320 самых значащих его компонент (которые определяются методом анализа главных компонент). Сгенерированные изображения, показанные слева направо, воспроизводят все больше деталей оригинала по мере того, как мы увеличиваем количество учитываемых компонент структурированного представления.
К примеру, в верхней строке картинок сначала воспроизводится базовая информация о том, что на изображении должны быть хоть какая-то еда и тарелка, а на поздних стадиях появляется уже информация о бутылке и деревянном столе внизу.
#нейронные_сети #популярное
Diep-Deep: вот так нейросеть пытается справиться с задачей генерации изображения по текстовому описанию "A sign that says deep learning".
Неплохая попытка, но в целом задача оказывается невыполненной, что авторы приписывают недостаточной разрешающей способности скрытого CLIP-представления, на основе которого производится генерация.
#нейронные_сети #цитаты
Неплохая попытка, но в целом задача оказывается невыполненной, что авторы приписывают недостаточной разрешающей способности скрытого CLIP-представления, на основе которого производится генерация.
#нейронные_сети #цитаты
Статья о социальной термодинамике 2.0, посвященная памяти Карла Маркса.
При помощи уравнения Ван-дер-Ваальса автор описывает переход от капитализма к коммунизму по мере развития производительных сил. При низком уровне их развития (что отвечает низкой температуре) у нас сосуществуют два общественных класса – пролетариат и буржуазия, – что отвечает разделению жидкой и газообразной фаз. При высоком же уровне развития производительных сил противоречия между классами стираются и наступает коммунизм, подобно тому, как при сверхкритической температуре исчезает различие между жидкостью и газом.
#термодинамика #общество #цитаты
При помощи уравнения Ван-дер-Ваальса автор описывает переход от капитализма к коммунизму по мере развития производительных сил. При низком уровне их развития (что отвечает низкой температуре) у нас сосуществуют два общественных класса – пролетариат и буржуазия, – что отвечает разделению жидкой и газообразной фаз. При высоком же уровне развития производительных сил противоречия между классами стираются и наступает коммунизм, подобно тому, как при сверхкритической температуре исчезает различие между жидкостью и газом.
#термодинамика #общество #цитаты
😁5🌚3
Квазиклассическое квантование Бора-Зоммерфельда подразумевает, что действие вдоль замкнутой траектории должно квантоваться как ∮p•dr = 2πħ(n+1/2), откуда можно найти квантованные энергии. В этой работе квазиклассическое квантование обобщено на системы с неэрмитовым гамильтонианом H и комплексным спектром энергий.
При этом классическая траектория движения, задаваемая вторым законом Ньютона d²r/dt² = –∂H/∂p, будет также комплексной. Авторы показывают, что для того, чтобы такая траектория – хоть и комплексная – была замкнутой, шаги во времени dt тоже должны быть комплексными. Найдя замкнутую траекторию в комплексном пространстве r, проходимую системой за комплексный период времени, можно найти квазиклассический спектр комплексных же энергий.
На рисунке показан пример комплексного осциллятора с комплексной частотой колебаний: при движении в комплексном времени (слева) траектория может быть сделана замкнутой, а при движении в вещественном времени (справа) замкнуть ее невозможно.
#неэрмитовы_системы
При этом классическая траектория движения, задаваемая вторым законом Ньютона d²r/dt² = –∂H/∂p, будет также комплексной. Авторы показывают, что для того, чтобы такая траектория – хоть и комплексная – была замкнутой, шаги во времени dt тоже должны быть комплексными. Найдя замкнутую траекторию в комплексном пространстве r, проходимую системой за комплексный период времени, можно найти квазиклассический спектр комплексных же энергий.
На рисунке показан пример комплексного осциллятора с комплексной частотой колебаний: при движении в комплексном времени (слева) траектория может быть сделана замкнутой, а при движении в вещественном времени (справа) замкнуть ее невозможно.
#неэрмитовы_системы
👍2