Авторы этой статьи сделали попытку описать возникновение эпистемологической стрелы времени на формально-математическом уровне. Они вводят три типа устройств, которые могут функционировать в качестве памяти, отличающиеся ролью, которую играет состояние самой памяти и части окружающего ее мира для восстановления информации о прошлом (или о будущем).
Память 1-го типа позволяет сделать выводы о состоянии окружающего мира w₁ в момент времени t₁ на основе знания о состоянии памяти m₀ в текущий момент времени t₀. Фраза «позволяет сделать выводы» означает большую величину взаимной информации между статистическими распределениями состояний w₁ и m₀. Это, в принципе, интуитивно понятно: наблюдая определенные состояния памяти в данный момент времени, мы сразу же делаем вывод о том, каково вероятное состояние окружающего мира в другой момент времени.
Память 2-го типа отличается тем, что для получения выводов о состоянии окружающего мира w₁ нам нужно знать не только текущее состояние памяти m₀, но и быть уверенными в том, что текущее состояние окружающего мира w₀ попадает в определенное подмножество состояний. Пример такой памяти появляется в компьютерах. Если мы знаем, что компьютер выполняет определенную программу (программа – это состояние w₀ части окружающего мира, внешней по отношению к памяти), то текущее состояние памяти позволяет понять, какими являются состояния компьютера в другие моменты времени. Примечательно, что память 2-го типа симметрична во времени: зная устройство программы, мы по текущему состоянию компьютерной памяти можем восстановить ход вычислений как в направлении прошлого, так и в направлении будущего. Еще пример памяти 2-го типа – Солнечная система, тоже эволюционирующая по «запрограммированным» законам небесной механики, где по текущему положению планет, их спутников и астероидов мы можем восстановить их положения как в прошлые моменты времени, так и в будущее.
Что же касается памяти 1-го типа, то единственная ее разновидность, которая реально может работать как память – это особый случай, который авторы называют памятью 3-го типа. Она отличается наложением дополнительных условий на состояние памяти m₁ в момент времени t₁ – тот самый момент, когда окружающий мир еще не провзаимодействовал с нашей памятью (взаимодействие произойдет в какой-то другой момент времени, промежуточный между t₁ и t₀). Если вспомнить лунные кратеры как пример памяти, то дополнительное условие состоит в том, что поверхность Луны в момент времени t₁ должна быть ровной – тогда наличие кратера (состояние «памяти») в текущий момент времени t₀ свидетельствует о взаимодействии Луны с метеоритом («окружающем миром») в момент времени, лежащий между t₁ и t₀.
Я не совсем понял смысл математических условий, наложенных на состояние памяти m₁, но в общих чертах они сводятся к тому, что состояние m₁ должно быть приготовлено в процессе сокращения числа состояний (state space collapse), превращающего более широкое множество состояний памяти в более узкое множество. По сути, это процесс инициализации памяти, приведения ее в «стертое» состояние, готовое к записи новой информации. Применительно к поверхности Луны это ее выравнивание: множество различных неровных конфигураций превращаются в единственную ровную. Как известно из термодинамики, процесс сокращения числа состояний памяти (то есть уменьшения ее энтропии) должен сопровождаться ростом энтропии остальной части Вселенной.
Таким образом, память 3-го типа может работать только в том случае, если ее «исходное» состояние в момент времени t₁ было приготовлено в ходе процесса, увеличивающего энтропию Вселенной. Это приводит к определенной направленности работы памяти – той самой эпистемологической стреле времени. Если процессы увеличения энтропии Вселенной идут преимущественно в одном направлении – в сторону увеличения переменной t, – то и память 3-го типа будет работать тоже лишь в этом направлении.
#популярное #объяснения #информация #термодинамика
Память 1-го типа позволяет сделать выводы о состоянии окружающего мира w₁ в момент времени t₁ на основе знания о состоянии памяти m₀ в текущий момент времени t₀. Фраза «позволяет сделать выводы» означает большую величину взаимной информации между статистическими распределениями состояний w₁ и m₀. Это, в принципе, интуитивно понятно: наблюдая определенные состояния памяти в данный момент времени, мы сразу же делаем вывод о том, каково вероятное состояние окружающего мира в другой момент времени.
Память 2-го типа отличается тем, что для получения выводов о состоянии окружающего мира w₁ нам нужно знать не только текущее состояние памяти m₀, но и быть уверенными в том, что текущее состояние окружающего мира w₀ попадает в определенное подмножество состояний. Пример такой памяти появляется в компьютерах. Если мы знаем, что компьютер выполняет определенную программу (программа – это состояние w₀ части окружающего мира, внешней по отношению к памяти), то текущее состояние памяти позволяет понять, какими являются состояния компьютера в другие моменты времени. Примечательно, что память 2-го типа симметрична во времени: зная устройство программы, мы по текущему состоянию компьютерной памяти можем восстановить ход вычислений как в направлении прошлого, так и в направлении будущего. Еще пример памяти 2-го типа – Солнечная система, тоже эволюционирующая по «запрограммированным» законам небесной механики, где по текущему положению планет, их спутников и астероидов мы можем восстановить их положения как в прошлые моменты времени, так и в будущее.
Что же касается памяти 1-го типа, то единственная ее разновидность, которая реально может работать как память – это особый случай, который авторы называют памятью 3-го типа. Она отличается наложением дополнительных условий на состояние памяти m₁ в момент времени t₁ – тот самый момент, когда окружающий мир еще не провзаимодействовал с нашей памятью (взаимодействие произойдет в какой-то другой момент времени, промежуточный между t₁ и t₀). Если вспомнить лунные кратеры как пример памяти, то дополнительное условие состоит в том, что поверхность Луны в момент времени t₁ должна быть ровной – тогда наличие кратера (состояние «памяти») в текущий момент времени t₀ свидетельствует о взаимодействии Луны с метеоритом («окружающем миром») в момент времени, лежащий между t₁ и t₀.
Я не совсем понял смысл математических условий, наложенных на состояние памяти m₁, но в общих чертах они сводятся к тому, что состояние m₁ должно быть приготовлено в процессе сокращения числа состояний (state space collapse), превращающего более широкое множество состояний памяти в более узкое множество. По сути, это процесс инициализации памяти, приведения ее в «стертое» состояние, готовое к записи новой информации. Применительно к поверхности Луны это ее выравнивание: множество различных неровных конфигураций превращаются в единственную ровную. Как известно из термодинамики, процесс сокращения числа состояний памяти (то есть уменьшения ее энтропии) должен сопровождаться ростом энтропии остальной части Вселенной.
Таким образом, память 3-го типа может работать только в том случае, если ее «исходное» состояние в момент времени t₁ было приготовлено в ходе процесса, увеличивающего энтропию Вселенной. Это приводит к определенной направленности работы памяти – той самой эпистемологической стреле времени. Если процессы увеличения энтропии Вселенной идут преимущественно в одном направлении – в сторону увеличения переменной t, – то и память 3-го типа будет работать тоже лишь в этом направлении.
#популярное #объяснения #информация #термодинамика
arXiv.org
Memory Systems, the Epistemic Arrow of Time, and the Second Law
The epistemic arrow of time is the fact that our knowledge of the past seems to be both of a different kind and more detailed than our knowledge of the future. Just like with the other arrows of...
В этой работе теоретически рассмотрены поверхностные плазмоны на графене, помещенном между двумя диэлектрическими средами, одна из которых пассивна (обладает диссипацией, Im ε > 0), а другая активна (обладает противоположной по знаку Im ε). Если сам графен не имеет диссипации, то вся система оказывается PT-симметричной, потому что ее активные и пассивные области меняются местами при пространственной инверсии.
Неэрмитовы PT-симметричные системы примечательны своими исключительными точками в пространстве параметров, где два чисто вещественных значения энергии смыкаются и превращаются в два комплексно сопряженных. Аналог этого явления виден и на графиках для вещественной kₓ´ и мнимой kₓ´´ частей волнового вектора как функции частоты ω: по мере роста ω два комплексно сопряженных волновых вектора kₓ (точки C и D) превращаются в два чисто вещественных (A и B), а затем снова в два комплексно сопряженных (E и F). Таким образом, на оси ω мы наблюдаем две исключительные точки.
#неэрмитовы_системы #графен #плазмоны
Неэрмитовы PT-симметричные системы примечательны своими исключительными точками в пространстве параметров, где два чисто вещественных значения энергии смыкаются и превращаются в два комплексно сопряженных. Аналог этого явления виден и на графиках для вещественной kₓ´ и мнимой kₓ´´ частей волнового вектора как функции частоты ω: по мере роста ω два комплексно сопряженных волновых вектора kₓ (точки C и D) превращаются в два чисто вещественных (A и B), а затем снова в два комплексно сопряженных (E и F). Таким образом, на оси ω мы наблюдаем две исключительные точки.
#неэрмитовы_системы #графен #плазмоны
👍1
Предел Либа-Робинсона – это один из квантовых пределов скорости, налагающих ограничения на скорости, с которыми квантовые системы могут менять свои состояния.
Как известно, в одномерной цепочке, где частицы могут перескакивать между соседними узлами, разделенными расстоянием a, с интегралом перескока J, дисперсия волн имеет вид E(k) = –2J cos(ka). Это означает, что групповая скорость возбуждений ∂E/ħ∂k = (2Ja/ħ)sin(ka) в такой системе не может превышать верхний предел 2Ja/ħ. Следовательно, любые сигналы не могут распространяться по цепочке быстрее некоторой предельной скорости, равной Ja/ħ по порядку величины– это и есть предел Либа-Робинсона.
В этой статье дается обзор всевозможных разновидностей пределов скорости для квантовых многочастичных систем: для распространения энергии, информации, квантовой запутанности и других корреляций. Примечательно, что они могут применяться и в статических задачах, давая, например, ограничения на протяженность квантовой запутанности в пространстве.
#квантовая_механика
Как известно, в одномерной цепочке, где частицы могут перескакивать между соседними узлами, разделенными расстоянием a, с интегралом перескока J, дисперсия волн имеет вид E(k) = –2J cos(ka). Это означает, что групповая скорость возбуждений ∂E/ħ∂k = (2Ja/ħ)sin(ka) в такой системе не может превышать верхний предел 2Ja/ħ. Следовательно, любые сигналы не могут распространяться по цепочке быстрее некоторой предельной скорости, равной Ja/ħ по порядку величины– это и есть предел Либа-Робинсона.
В этой статье дается обзор всевозможных разновидностей пределов скорости для квантовых многочастичных систем: для распространения энергии, информации, квантовой запутанности и других корреляций. Примечательно, что они могут применяться и в статических задачах, давая, например, ограничения на протяженность квантовой запутанности в пространстве.
#квантовая_механика
Любопытная работа, где предсказывается кооперативное усиление мощности и эффективности работы тепловой машины, состоящей из двух гармонических осцилляторов, взаимодействующих с одними и теми же термостатами.
Термостаты описываются моделью Кальдейры-Леггетта (это система большого числа невзаимодействующих осцилляторов), а цикл работы тепловой машины задается периодическими модуляциями силы связи обоих осцилляторов, составляющих рабочее тело, с горячим термостатом. Если приближенно исключить термостаты, динамика осцилляторов описывается системой уравнений, связанных диссипативным членом γ₂ через термостаты (прямая связь между осцилляторами отсутствует). В такой системе возникает коллективная мода, затухание которой парадоксальным образом исчезает в пределе сильной диссипации γ₂ → ∞.
Именно благодаря ей мощность тепловой машины при больших γ₂ оказывается гораздо выше, чем в случае совокупности двух независимых тепловых машин, как показано на рисунке сравнением красных и синих точек.
#квантовая_термодинамика
Термостаты описываются моделью Кальдейры-Леггетта (это система большого числа невзаимодействующих осцилляторов), а цикл работы тепловой машины задается периодическими модуляциями силы связи обоих осцилляторов, составляющих рабочее тело, с горячим термостатом. Если приближенно исключить термостаты, динамика осцилляторов описывается системой уравнений, связанных диссипативным членом γ₂ через термостаты (прямая связь между осцилляторами отсутствует). В такой системе возникает коллективная мода, затухание которой парадоксальным образом исчезает в пределе сильной диссипации γ₂ → ∞.
Именно благодаря ей мощность тепловой машины при больших γ₂ оказывается гораздо выше, чем в случае совокупности двух независимых тепловых машин, как показано на рисунке сравнением красных и синих точек.
#квантовая_термодинамика
А вот еще картинка из статьи из предыдущего поста: здесь для изученной тепловой машины авторы находили фронт Парето в пространстве выделяемой ей мощности P и КПД ее работы η.
Фронтом Парето называется множество таких точек в пространстве характеристик системы, где для увеличения одной из них обязательно придется уменьшить другую. То есть это множество оптимальных комбинаций, демонстрирующих пределы эффективности, за которые уже не перешагнуть.
На рисунке показаны положения фронта Парето на плоскости (η, P) при разных отношениях частот двух осцилляторов. Каждая точка фронта, демонстрирующая компромисс между мощностью и КПД, была получена оптимизацией по всем возможным циклам, то есть всем возможным периодическим зависимостям сил связи каждого осциллятора с каждым термостатом от времени. Можно видеть, что в случае кооперативной системы (синие точки) фронт Парето продвигается значительно дальше, чем в случае системы двух отдельных, несвязанных осцилляторов (оранжевые точки).
#квантовая_термодинамика
Фронтом Парето называется множество таких точек в пространстве характеристик системы, где для увеличения одной из них обязательно придется уменьшить другую. То есть это множество оптимальных комбинаций, демонстрирующих пределы эффективности, за которые уже не перешагнуть.
На рисунке показаны положения фронта Парето на плоскости (η, P) при разных отношениях частот двух осцилляторов. Каждая точка фронта, демонстрирующая компромисс между мощностью и КПД, была получена оптимизацией по всем возможным циклам, то есть всем возможным периодическим зависимостям сил связи каждого осциллятора с каждым термостатом от времени. Можно видеть, что в случае кооперативной системы (синие точки) фронт Парето продвигается значительно дальше, чем в случае системы двух отдельных, несвязанных осцилляторов (оранжевые точки).
#квантовая_термодинамика
Формула Онзагера-Мэчлапа (Onsager-Machlup formula) – это некий аналог фейнмановского интеграла по путям, только для процесса классической диффузии частиц, или броуновского движения.
Рассмотрим безынерционное (overdamped) движение частицы, описываемое уравнением Ланжевена, показанным на рисунке сверху. На частицу действует зависящая от координат сила F (не обязательно потенциальная) и зависящая от времени сила случайного шума, масштабированная на коэффициент диффузии D. Тогда вероятность реализации пути r(t) будет задаваться интегралом вдоль этого пути, показанным внизу.
Первое слагаемое в экспоненте заставляет частицу двигаться со скоростью вдоль силы F и штрафует за отклонения – тем слабее, чем больше коэффициент диффузии D. Второе слагаемое штрафует путь (делает его менее вероятным) за посещение областей с положительной дивергенцией F, потому что div F > 0 означает, что сила F выталкивает частицу из такой области наружу.
#стохастическая_термодинамика #объяснения
Рассмотрим безынерционное (overdamped) движение частицы, описываемое уравнением Ланжевена, показанным на рисунке сверху. На частицу действует зависящая от координат сила F (не обязательно потенциальная) и зависящая от времени сила случайного шума, масштабированная на коэффициент диффузии D. Тогда вероятность реализации пути r(t) будет задаваться интегралом вдоль этого пути, показанным внизу.
Первое слагаемое в экспоненте заставляет частицу двигаться со скоростью вдоль силы F и штрафует за отклонения – тем слабее, чем больше коэффициент диффузии D. Второе слагаемое штрафует путь (делает его менее вероятным) за посещение областей с положительной дивергенцией F, потому что div F > 0 означает, что сила F выталкивает частицу из такой области наружу.
#стохастическая_термодинамика #объяснения
🔥2👍1
Стильно выглядящая солнечная батарея: она изготовлена с использованием так называемого черного кремния: обычного кремния, поверхность которого покрыта массивом кремниевых же наночастиц. Образующаяся метаповерхность хорошо поглощает свет в значительной части видимого диапазона.
#фотоника
#фотоника
А это – в представлении художника – плазмоэлектрический эффект: возникновение разности потенциалов при облучении светом метаповерхности с массивом отверстий в металле, обусловленное возбуждением плазмонов.
#плазмоны
#плазмоны
🔥1
Изобретение долгой краткосрочной памяти (long short-term memory), сделанное в 1997 году, произвело настоящую революцию в практике создания рекуррентных нейронных сетей, работающих с длинными последовательностями сигналов: текстами, речью и другими звуками, видеопотоками и т.д.
В отличие от сетей прямого распространения (feedforward network), через которую сигналы проходят только один раз и в одну сторону от входа к выходу, рекуррентная нейронная сеть допускает распространение сигналов в любые стороны, как в человеческом мозге. Так можно заставлять нейросеть обрабатывать входные данные, которые не имеют определенной размерности (как, например, единственная пиксельная картинка, которую нужно распознать), а последовательно поступают в течение длительного времени. Простейшая организация нейросети для такой задачи – это замыкание ее в цикл, когда выходные сигналы h нейросети подаются обратно на ее вход вместе со входными данными x. Тогда на каждом шаге времени t нейронная сеть будет обрабатывать совокупность входных данных x(t) и выходных данных h(t–1) – результатов «переваривания» всех предшествующих входных данных x(t–1), x(t–2) и т.д., формируя новые выходные данные h(t) = f(x(t), h(t–1)), которые на следующем шаге снова поступят на ее вход.
Проблема такого подхода в сложности обучения получившейся сети. Для подгонки параметров сети w – весов межнейронных связей и смещений – с целью уменьшения функции ошибок L нужно вычислять градиент ∂L/∂w. Это делается при помощи алгоритма обратного распространения ошибки: вектор величины ошибок последовательно прогоняется от выходного слоя нейронов к входному задом наперед, на каждом шаге умножаясь на некие матрицы. В случае описанной выше рекуррентной архитектуры этот проход через нейросеть задом наперед нужно повторять множество раз – точно так же, как при работе сети сами сигналы многократно проходят через одну и ту же последовательность нейронных слоев. Фактически получается умножение вектора ошибок на одну и ту же совокупность матриц M, возведенную в большую степень: а это приводит к тому, что ошибки либо улетают на бесконечность (если мы попали на собственный вектор M с собственным значением больше 1), либо экспоненциально падают почти до нуля (если собственное значение меньше 1). Это называется проблемой взрывающихся градиентов и проблемой исчезающих градиентов.
Долгая краткосрочная память позволяет решить эту проблему путем распутывания сигналов данных и сигналов ошибок. Этот метод основан на включении в нейронную сеть ячеек памяти, входы и выходы которых связаны с остальными слоями нейронов мультипликативными вентилями – операциями поэлементного умножения. А именно:
– Вектор значений c(t) в ячейках памяти частично складывается из входного сигнала i(t), умноженного поэлементно на значения входного вентиля g(t).
– Другая часть вектора c(t) формируется старым содержимым памяти c(t–1), умноженным на значения вентиля забывания f(t).
– На выход ячейки памяти – который, в простейшем случае, дает выходной сигнал h(t) всей сети – подается ее содержимое c(t), умноженное на значение выходного вентиля o(t).
При этом все значения на вентилях g(t), f(t), o(t) вычисляются отдельными слоями нейронов, на основе сигналов x(t) и h(t–1), поступающих на вход всей сети.
При вычислении градиента функции ошибок в такой архитектуре сети некоторые производные искусственно зануляются: а именно, считается, что ошибки сигналов на выходе каждого мультипликативного вентиля обусловлены только ошибками значения самого вентиля (g(t), f(t) либо o(t)), а не того входного сигнала, который на него умножается. Это позволяет избежать проблемы взрывающихся и исчезающих градиентов, потому что бесконечный цикл прохода ошибок по одним и тем же слоям нейронов размыкается. Создается так называемая «карусель ошибок», при которой ошибка продолжает циркулировать внутри ячейки памяти и через вентили, но ее величина остается стабильной. По крайней мере, так я понял довольно тяжеловесные объяснения авторов оригинальной работы.
#нейронные_сети #объяснения #популярное
В отличие от сетей прямого распространения (feedforward network), через которую сигналы проходят только один раз и в одну сторону от входа к выходу, рекуррентная нейронная сеть допускает распространение сигналов в любые стороны, как в человеческом мозге. Так можно заставлять нейросеть обрабатывать входные данные, которые не имеют определенной размерности (как, например, единственная пиксельная картинка, которую нужно распознать), а последовательно поступают в течение длительного времени. Простейшая организация нейросети для такой задачи – это замыкание ее в цикл, когда выходные сигналы h нейросети подаются обратно на ее вход вместе со входными данными x. Тогда на каждом шаге времени t нейронная сеть будет обрабатывать совокупность входных данных x(t) и выходных данных h(t–1) – результатов «переваривания» всех предшествующих входных данных x(t–1), x(t–2) и т.д., формируя новые выходные данные h(t) = f(x(t), h(t–1)), которые на следующем шаге снова поступят на ее вход.
Проблема такого подхода в сложности обучения получившейся сети. Для подгонки параметров сети w – весов межнейронных связей и смещений – с целью уменьшения функции ошибок L нужно вычислять градиент ∂L/∂w. Это делается при помощи алгоритма обратного распространения ошибки: вектор величины ошибок последовательно прогоняется от выходного слоя нейронов к входному задом наперед, на каждом шаге умножаясь на некие матрицы. В случае описанной выше рекуррентной архитектуры этот проход через нейросеть задом наперед нужно повторять множество раз – точно так же, как при работе сети сами сигналы многократно проходят через одну и ту же последовательность нейронных слоев. Фактически получается умножение вектора ошибок на одну и ту же совокупность матриц M, возведенную в большую степень: а это приводит к тому, что ошибки либо улетают на бесконечность (если мы попали на собственный вектор M с собственным значением больше 1), либо экспоненциально падают почти до нуля (если собственное значение меньше 1). Это называется проблемой взрывающихся градиентов и проблемой исчезающих градиентов.
Долгая краткосрочная память позволяет решить эту проблему путем распутывания сигналов данных и сигналов ошибок. Этот метод основан на включении в нейронную сеть ячеек памяти, входы и выходы которых связаны с остальными слоями нейронов мультипликативными вентилями – операциями поэлементного умножения. А именно:
– Вектор значений c(t) в ячейках памяти частично складывается из входного сигнала i(t), умноженного поэлементно на значения входного вентиля g(t).
– Другая часть вектора c(t) формируется старым содержимым памяти c(t–1), умноженным на значения вентиля забывания f(t).
– На выход ячейки памяти – который, в простейшем случае, дает выходной сигнал h(t) всей сети – подается ее содержимое c(t), умноженное на значение выходного вентиля o(t).
При этом все значения на вентилях g(t), f(t), o(t) вычисляются отдельными слоями нейронов, на основе сигналов x(t) и h(t–1), поступающих на вход всей сети.
При вычислении градиента функции ошибок в такой архитектуре сети некоторые производные искусственно зануляются: а именно, считается, что ошибки сигналов на выходе каждого мультипликативного вентиля обусловлены только ошибками значения самого вентиля (g(t), f(t) либо o(t)), а не того входного сигнала, который на него умножается. Это позволяет избежать проблемы взрывающихся и исчезающих градиентов, потому что бесконечный цикл прохода ошибок по одним и тем же слоям нейронов размыкается. Создается так называемая «карусель ошибок», при которой ошибка продолжает циркулировать внутри ячейки памяти и через вентили, но ее величина остается стабильной. По крайней мере, так я понял довольно тяжеловесные объяснения авторов оригинальной работы.
#нейронные_сети #объяснения #популярное
MIT Press
Long Short-Term Memory
Abstract. Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address…
👍3🤨1
А вот картинка и формулы, иллюстрирующие работу долгой краткосрочной памяти, которая на словах описывалась в предыдущем посте.
Каждый кружочек g, f, o – это слой нейронов, на который подаются входные данные x, поступившие на текущем временном шаге, и выходные данные h с предыдущего шага. Так формируются значения вентилей от 0 до 1, которые поэлементно умножаются (крестики) на другие сигналы: обработанный входной сигнал i, а также значения c ячейки памяти, поступающие как на выход сети (вправо), так и обратно в память (снизу).
Вентили позволяют нейросети управляемым образом открывать ячейку памяти для записи новых значений (через входной вентиль g), сохранять значения в памяти либо стирать их (через вентиль забывания f) и выводить значения из памяти наружу (выходной вентиль o). Таким образом, сеть может долгое время удерживать в памяти результаты обработки данных, поступивших ей на вход давным-давно, если они вдруг понадобятся, «срезонировав» с текущими данными.
#нейронные_сети #объяснения #популярное
Каждый кружочек g, f, o – это слой нейронов, на который подаются входные данные x, поступившие на текущем временном шаге, и выходные данные h с предыдущего шага. Так формируются значения вентилей от 0 до 1, которые поэлементно умножаются (крестики) на другие сигналы: обработанный входной сигнал i, а также значения c ячейки памяти, поступающие как на выход сети (вправо), так и обратно в память (снизу).
Вентили позволяют нейросети управляемым образом открывать ячейку памяти для записи новых значений (через входной вентиль g), сохранять значения в памяти либо стирать их (через вентиль забывания f) и выводить значения из памяти наружу (выходной вентиль o). Таким образом, сеть может долгое время удерживать в памяти результаты обработки данных, поступивших ей на вход давным-давно, если они вдруг понадобятся, «срезонировав» с текущими данными.
#нейронные_сети #объяснения #популярное
А вот некоторые результаты, которые изобретатели долгой краткосрочной памяти – Зепп Хохрайтер и Юрген Шмидхубер – сразу же продемонстрировали на практике.
▪️ Нейросеть в виде ячейки долгой краткосрочной памяти заставляли предсказывать следующую букву грамматики Ребера по предшествующим буквам. Здесь не требуется долгое удержание значений в памяти, поскольку грамматика Ребера содержит лишь близкие корреляции, но это популярная модель для тестирования методов машинного обучения. Новая нейросеть успешно справилась с задачей угадывая символы более чем в 97% случаях, в отличие от других рекуррентных архитектур.
▪️ Наборы символов, разделенные длинными последовательностями: нейросеть учат распознавать последовательности символов вида (x … x), (y … y), (e, x … e, x), (b, y … b, y), где многоточия обозначают несколько сотен «отвлекающих» символов – либо каждый раз одних и тех же, либо случайно меняющихся. Нейросеть должна сопоставить символы в самом начале последовательности с символами в самом ее конце, проигнорировав все промежуточные. Это значит, что начальные символы она должна очень долго удерживать в памяти. Новая архитектура отлично справилась с этими задачами на 100%, в то время как другие варианты сетей справлялись с ними лишь с вероятностью успеха 22-78%, а некоторые вообще не справились.
▪️ Задачи условного сложения и умножения, которые никогда раньше не решались рекуррентными сетями: на вход подается последовательность пар чисел (xᵢ, yᵢ), и нейросеть должна посчитать либо сумму всех xᵢ, либо произведение всех xᵢ, для которых yᵢ = 1. Как видно, здесь требуются весьма нетривиальные операции с комбинациями входных чисел и содержимым памяти.
#нейронные_сети #популярное
▪️ Нейросеть в виде ячейки долгой краткосрочной памяти заставляли предсказывать следующую букву грамматики Ребера по предшествующим буквам. Здесь не требуется долгое удержание значений в памяти, поскольку грамматика Ребера содержит лишь близкие корреляции, но это популярная модель для тестирования методов машинного обучения. Новая нейросеть успешно справилась с задачей угадывая символы более чем в 97% случаях, в отличие от других рекуррентных архитектур.
▪️ Наборы символов, разделенные длинными последовательностями: нейросеть учат распознавать последовательности символов вида (x … x), (y … y), (e, x … e, x), (b, y … b, y), где многоточия обозначают несколько сотен «отвлекающих» символов – либо каждый раз одних и тех же, либо случайно меняющихся. Нейросеть должна сопоставить символы в самом начале последовательности с символами в самом ее конце, проигнорировав все промежуточные. Это значит, что начальные символы она должна очень долго удерживать в памяти. Новая архитектура отлично справилась с этими задачами на 100%, в то время как другие варианты сетей справлялись с ними лишь с вероятностью успеха 22-78%, а некоторые вообще не справились.
▪️ Задачи условного сложения и умножения, которые никогда раньше не решались рекуррентными сетями: на вход подается последовательность пар чисел (xᵢ, yᵢ), и нейросеть должна посчитать либо сумму всех xᵢ, либо произведение всех xᵢ, для которых yᵢ = 1. Как видно, здесь требуются весьма нетривиальные операции с комбинациями входных чисел и содержимым памяти.
#нейронные_сети #популярное
MIT Press
Long Short-Term Memory
Abstract. Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address…
В этой работе сотрудников Google 2014 года долгая краткосрочная память использовалась для машинного перевода предложений с английского языка на французский. В принципе, ответы на вопросы – это похожая по структуре задача, где последовательности входных слов нужно сопоставить последовательность выходных слов. Так что эту работу можно считать ранней стадией разработки нейросети ChatGPT.
Архитектура нейросети довольно простая: она состоит из двух ячеек долгой краткосрочной памяти, хотя и не простой, а так называемой глубокой памяти: внутри ячейки сигналы проходят через 4 слоя по 1000 нейронов каждый. Размерность сигнала 1000 отвечает размерности пространства, на которое отображается каждое из слов английского и французского языков. На первую ячейку памяти подается исходное предложение на английском, та ее переваривает и выдает окончательный сигнал – «скрытое представление» предложения, содержащее его смысл в виде вектора в 1000-мерном пространстве. Этот сигнал затем поступает на вторую ячейку памяти, которая, циклически работая, выдает переведенное предложение на английском – слово за словом, пока не выдаст специальный символ конца предложения. Долгая краткосрочная память особенно удобна здесь тем, что она может работать с последовательностями слов произвольной длины.
Построенная модель показала в целом заметно лучшие результаты, чем другие методы машинного перевода. Интересно, что результаты получились гораздо лучше при обращении порядка слов во входном предложении: если подавать на нейросеть последовательность CBA вместо исходной последовательности слов ABC, то ей легче связывать слово A, которое окажется последним на входе, с его переведенным аналогом, который окажется на выходе первым и т.д.
#нейронные_сети #популярное
Архитектура нейросети довольно простая: она состоит из двух ячеек долгой краткосрочной памяти, хотя и не простой, а так называемой глубокой памяти: внутри ячейки сигналы проходят через 4 слоя по 1000 нейронов каждый. Размерность сигнала 1000 отвечает размерности пространства, на которое отображается каждое из слов английского и французского языков. На первую ячейку памяти подается исходное предложение на английском, та ее переваривает и выдает окончательный сигнал – «скрытое представление» предложения, содержащее его смысл в виде вектора в 1000-мерном пространстве. Этот сигнал затем поступает на вторую ячейку памяти, которая, циклически работая, выдает переведенное предложение на английском – слово за словом, пока не выдаст специальный символ конца предложения. Долгая краткосрочная память особенно удобна здесь тем, что она может работать с последовательностями слов произвольной длины.
Построенная модель показала в целом заметно лучшие результаты, чем другие методы машинного перевода. Интересно, что результаты получились гораздо лучше при обращении порядка слов во входном предложении: если подавать на нейросеть последовательность CBA вместо исходной последовательности слов ABC, то ей легче связывать слово A, которое окажется последним на входе, с его переведенным аналогом, который окажется на выходе первым и т.д.
#нейронные_сети #популярное
arXiv.org
Sequence to Sequence Learning with Neural Networks
Deep Neural Networks (DNNs) are powerful models that have achieved excellent performance on difficult learning tasks. Although DNNs work well whenever large labeled training sets are available,...
Еще интересное из статьи из предыдущего поста: можно попробовать посмотреть, а как в принципе выглядит скрытое представление исходного предложения, которое нейросеть прочитала и «поняла», чтобы затем на его основе сгенерировать перевод.
Это точка в 1000 мерном пространстве, но набор нескольких таких точек можно попытаться спроецировать на двумерную плоскость (сделав для них, фактически, анализ главных компонент). На рисунке показано, как выглядят такие проекции наборов точек, описывающих понятый нейросетью «смысл» наборов предложений, отличающихся заменой слов на синонимы либо перестановкой слов.
Видно, что нейросеть правильно сгруппировала предложения, имеющие близкий смысл (например, сверху, где Мэри любит или уважает Джона) и отдельно сгруппировала предложения, имеющие противоположный смысл (Джон любит или уважает Мэри) и полученные из первых простой перестановкой слов. Таким образом, модель правильно учитывает не только сами слова, но и порядок их расположения.
#нейронные_сети #популярное
Это точка в 1000 мерном пространстве, но набор нескольких таких точек можно попытаться спроецировать на двумерную плоскость (сделав для них, фактически, анализ главных компонент). На рисунке показано, как выглядят такие проекции наборов точек, описывающих понятый нейросетью «смысл» наборов предложений, отличающихся заменой слов на синонимы либо перестановкой слов.
Видно, что нейросеть правильно сгруппировала предложения, имеющие близкий смысл (например, сверху, где Мэри любит или уважает Джона) и отдельно сгруппировала предложения, имеющие противоположный смысл (Джон любит или уважает Мэри) и полученные из первых простой перестановкой слов. Таким образом, модель правильно учитывает не только сами слова, но и порядок их расположения.
#нейронные_сети #популярное
С ума сойти, у этой статьи сотрудников Google про использование долгой краткосрочной памяти для машинного перевода 23664 цитирования, набравшихся меньше чем за 10 лет.
Для сравнения:
- У эпохальной статьи Бардина, Купера и Шриффера по теории сверхпроводимости (1957 г.) всего 9265 цитирований.
- Статья Фано о резонансах Фано (1961 г.), называемая в Википедии одной из самых цитируемых работ по физике, имеет 9432 цитирования.
- Статья Хоэнберга и Кона, где сообщается об изобретении метода функционала плотности (1964 г.), имеет 38993 цитирования.
#цитаты
Для сравнения:
- У эпохальной статьи Бардина, Купера и Шриффера по теории сверхпроводимости (1957 г.) всего 9265 цитирований.
- Статья Фано о резонансах Фано (1961 г.), называемая в Википедии одной из самых цитируемых работ по физике, имеет 9432 цитирования.
- Статья Хоэнберга и Кона, где сообщается об изобретении метода функционала плотности (1964 г.), имеет 38993 цитирования.
#цитаты
👍7
В этой работе долгая краткосрочная память была использована в комбинации с механизмом внимания для обучения нейронной сети задачам понимания текстов.
От обычной архитектуры с долгой кратковременной памятью отличие здесь в том, что нейросеть сопоставляет текущее слово x(t), которое поступает ей на вход, с о всеми предыдущими выходными сигналами h(t–1), h(t–2), … и использует для расчета значений вентилей и обновления состояния памяти c(t) только те предыдущие состояния памяти и те предыдущие выходные сигналы, которые хорошо «резонируют» с текущим словом. Иными словами, при анализе каждого слова нейросеть обращает внимание на результаты обработки предшествующих слов, проводя между разными словами в предложении смысловые связи.
На рисунке показана пара примеров того, при решении задачи о том, выражает ли предложение положительное или отрицательное отношение к описываемому объекту, нейросеть в первую очередь связывает между собой важные по смыслу ключевые слова.
#нейронные_сети #популярное
От обычной архитектуры с долгой кратковременной памятью отличие здесь в том, что нейросеть сопоставляет текущее слово x(t), которое поступает ей на вход, с о всеми предыдущими выходными сигналами h(t–1), h(t–2), … и использует для расчета значений вентилей и обновления состояния памяти c(t) только те предыдущие состояния памяти и те предыдущие выходные сигналы, которые хорошо «резонируют» с текущим словом. Иными словами, при анализе каждого слова нейросеть обращает внимание на результаты обработки предшествующих слов, проводя между разными словами в предложении смысловые связи.
На рисунке показана пара примеров того, при решении задачи о том, выражает ли предложение положительное или отрицательное отношение к описываемому объекту, нейросеть в первую очередь связывает между собой важные по смыслу ключевые слова.
#нейронные_сети #популярное
Небольшой обзорчик по нанофотонике – всевозможным усилиям, направленным на то, чтобы сжать свет, имеющий длину волны порядка микрона, на размеры десятков нанометров или меньше, и при помощи этого реализовывать эффекты, невозможные в традиционной оптике.
Сжатие света можно осуществлять при помощи дефектов или щелей в фотонных кристаллах (A), металлических пластин (B) или наночастиц (C). При сжатии электрическое поле света усиливается на порядки, так что можно усиливать его взаимодействие с веществом. К примеру, в экспериментах достигнуто более чем 1000-кратное усиление поглощения и испускания фотонов молекулами, расположенными вблизи наночастиц.
Еще одна возможность, открываемая манипуляциями светом на наномасштабах – это создание эффективного магнитного отклика на основе чисто электрического при помощи киральных металлических структур (D). Отдельно интересны метаповерхности (E): они дают возможность манипулировать светом и при этом слабо его поглощают благодаря малой толщине.
#фотоника #электродинамика
Сжатие света можно осуществлять при помощи дефектов или щелей в фотонных кристаллах (A), металлических пластин (B) или наночастиц (C). При сжатии электрическое поле света усиливается на порядки, так что можно усиливать его взаимодействие с веществом. К примеру, в экспериментах достигнуто более чем 1000-кратное усиление поглощения и испускания фотонов молекулами, расположенными вблизи наночастиц.
Еще одна возможность, открываемая манипуляциями светом на наномасштабах – это создание эффективного магнитного отклика на основе чисто электрического при помощи киральных металлических структур (D). Отдельно интересны метаповерхности (E): они дают возможность манипулировать светом и при этом слабо его поглощают благодаря малой толщине.
#фотоника #электродинамика
Интересный эксперимент, где на примере одномерного атомного газа было продемонстрировано, что в квантовой многочастичной системе термализация – установление теплового равновесия – распространяется в пространстве с конечной скоростью.
Вытянутый в нить бозе-конденсированный газ атомов рубидия аккуратно расщеплялся на две параллельные нити, квантовые состояния которых с течением времени начинают расходиться из-за хаотичности идущей в них термализации.
Интерференционными измерениями можно отслеживать, как с течением времени спадает корреляционная функция C = Re<exp{iφ(z,t) – iφ(z′,t)}> относительной фазы φ = θ₁ – θ₂ двух конденсатов.
Как видно на рисунке, ростом расстояния z – z′ она спадает экспоненциально до какого-то предельного расстояния d, после чего выходит на константу. А само это предельное расстояние d = 2ct линейно растет с течением времени t, прошедшего после разделения нитей, с удвоенной характерной скоростью возбуждений c, образующихся в ходе термализации.
#атомные_газы #квантовая_термодинамика
Вытянутый в нить бозе-конденсированный газ атомов рубидия аккуратно расщеплялся на две параллельные нити, квантовые состояния которых с течением времени начинают расходиться из-за хаотичности идущей в них термализации.
Интерференционными измерениями можно отслеживать, как с течением времени спадает корреляционная функция C = Re<exp{iφ(z,t) – iφ(z′,t)}> относительной фазы φ = θ₁ – θ₂ двух конденсатов.
Как видно на рисунке, ростом расстояния z – z′ она спадает экспоненциально до какого-то предельного расстояния d, после чего выходит на константу. А само это предельное расстояние d = 2ct линейно растет с течением времени t, прошедшего после разделения нитей, с удвоенной характерной скоростью возбуждений c, образующихся в ходе термализации.
#атомные_газы #квантовая_термодинамика
В этом эксперименте обнаружена спонтанная генерация циркулирующих токов экситон-поляритонного бозе-конденсата при нерезонансной накачке.
Луч накачки имеет форму кольца, которое для бозе-конденсата служит источником новых поляритонов и одновременно отталкивающим потенциалом. Как показано на первой строке диаграмм для амплитуды и фазы люминесцентного излучения, фазовый профиль образовавшегося облака конденсата внутри кольца имеет странный вид со скачком фазы на величину π вдоль диаметра. Но амплитуда конденсата в этом месте не проваливается до нуля (как должно быть на топологическом дефекте). Как считают авторы, это свидетельствует о том, что наблюдаемый скачок фазы – это результат усреднения токов, случайно меняющих свое направление.
Если добавить к лучу накачки еще один небольшой лазерный луч сбоку, то круговая симметрия системы нарушается, давая начало спонтанно вращающемуся конденсату: либо по часовой стрелке (вторая строка диаграмм), либо против часовой (третья строка).
#поляритоны #бозе_конденсация
Луч накачки имеет форму кольца, которое для бозе-конденсата служит источником новых поляритонов и одновременно отталкивающим потенциалом. Как показано на первой строке диаграмм для амплитуды и фазы люминесцентного излучения, фазовый профиль образовавшегося облака конденсата внутри кольца имеет странный вид со скачком фазы на величину π вдоль диаметра. Но амплитуда конденсата в этом месте не проваливается до нуля (как должно быть на топологическом дефекте). Как считают авторы, это свидетельствует о том, что наблюдаемый скачок фазы – это результат усреднения токов, случайно меняющих свое направление.
Если добавить к лучу накачки еще один небольшой лазерный луч сбоку, то круговая симметрия системы нарушается, давая начало спонтанно вращающемуся конденсату: либо по часовой стрелке (вторая строка диаграмм), либо против часовой (третья строка).
#поляритоны #бозе_конденсация
Познавательная статья с небольшим обзором о связи между NP-трудными вычислительными задачами и теорией спиновых стекол, а также теорией обучения нейронных сетей.
Действительно, задачи комбинаторной оптимизации – например, задача коммивояжера, поиск максимальной клики или максимального разреза графа – сводятся к поиску глобального минимума функции ошибок в некотором многомерном пространстве. Математически это эквивалентно поиску основного состояния спинового стекла – большого числа классических спинов, соединенных случайными ферро- и антиферромагнитными взаимодействиями. Задача обучения нейросети – тоже поиск минимума функции ошибок в пространстве ее параметров.
Как и в случае спинового стекла, в задачах оптимизации существует фазовый переход между «упорядоченным» состоянием, где поиск глобального минимума сравнительно прост, и «аморфной» (или трудной) фазой, где потенциальный ландшафт становится сильно изрезанным с большим числом локальных минимумов, разделенных высокими барьерами.
#стекла #оптимизация
Действительно, задачи комбинаторной оптимизации – например, задача коммивояжера, поиск максимальной клики или максимального разреза графа – сводятся к поиску глобального минимума функции ошибок в некотором многомерном пространстве. Математически это эквивалентно поиску основного состояния спинового стекла – большого числа классических спинов, соединенных случайными ферро- и антиферромагнитными взаимодействиями. Задача обучения нейросети – тоже поиск минимума функции ошибок в пространстве ее параметров.
Как и в случае спинового стекла, в задачах оптимизации существует фазовый переход между «упорядоченным» состоянием, где поиск глобального минимума сравнительно прост, и «аморфной» (или трудной) фазой, где потенциальный ландшафт становится сильно изрезанным с большим числом локальных минимумов, разделенных высокими барьерами.
#стекла #оптимизация
👍2
А в этой работе обсуждается щель между перекрытиями (overlap gap) – свойство трудных оптимизационных задач, налагающее фундаментальные ограничения на эффективность многих направленных на их решение эвристических алгоритмов.
Это свойство заключается в следующим: рассмотрим функцию потерь трудной оптимизационной задачи L(σ) σ. Конфигурации, для которых L(σ) ≤ L* + μ, где L* – типичное положение глобального минимума функции потерь на множестве случайных примеров задач данного класса, μ > 0, можно назвать μ-оптимальными, то есть они не хуже «наилучшей» лишь на величину μ. Тогда расстояние d(σ, ξ) между любыми двумя μ-оптимальными конфигурациями σ и ξ, должно быть либо меньше ν₁, либо больше ν₂, где ν₂ > ν₁.
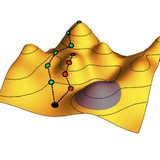
Графически это свойство показано на рисунке: оно говорит о том, что близкие к оптимуму конфигурации разбиваются на кластеры: любые две из них либо близки и попадают в один кластер (когда d(σ, ξ) < ν₁), либо далеки и попадают в разные кластеры (d(σ, ξ) > ν₂).
#стекла #оптимизация
Это свойство заключается в следующим: рассмотрим функцию потерь трудной оптимизационной задачи L(σ) σ. Конфигурации, для которых L(σ) ≤ L* + μ, где L* – типичное положение глобального минимума функции потерь на множестве случайных примеров задач данного класса, μ > 0, можно назвать μ-оптимальными, то есть они не хуже «наилучшей» лишь на величину μ. Тогда расстояние d(σ, ξ) между любыми двумя μ-оптимальными конфигурациями σ и ξ, должно быть либо меньше ν₁, либо больше ν₂, где ν₂ > ν₁.
Графически это свойство показано на рисунке: оно говорит о том, что близкие к оптимуму конфигурации разбиваются на кластеры: любые две из них либо близки и попадают в один кластер (когда d(σ, ξ) < ν₁), либо далеки и попадают в разные кластеры (d(σ, ξ) > ν₂).
#стекла #оптимизация
Щель между перекрытиями, о которой говорилось в предыдущем посте, налагает ограничения на эффективность быстрых эвристических алгоритмов, призванных решать трудные оптимизационные задачи.
Действительно, многие быстрые алгоритмы полиномиальной трудоемкости являются стабильными: то есть даваемые ими решения задачи слабо меняются при слабых изменениях условии задачи (например, при удалении единственного ребра большого графа, в котором нужно найти максимальную клику). Кластеризация же решений задачи, вытекающая из существования щели между перекрытиями, говорит о том, что не только наилучшее (тот самый единственный глобальный минимум функции потерь), но и близкие к наилучшему решения могут резко и непредсказуемо меняться при изменении условий задачи. Быстрый эвристический алгоритм, попадающий в кластер почти оптимальных решений и потому дающий хороший результат на одном экземпляре задачи, может дать куда худший результат при слегка измененных условиях задачи – потому что этот кластер может уже стать сильно неоптимальным.
С этим свойством, вероятно, связано и наблюдающийся в некоторых оптимизационных задачах существенный разрыв между типичным и алгоритмическим оптимумами. Что это такое, можно понять на примере задачи поиска максимальной клики (подмножества узлов, которые все попарно соединены между собой) в случайном графе Эрдёша-Реньи, где любые два узла соединены или не соединены ребром с вероятностью 1/2. Известно, что при общем числе узлов N >> 1 типичный размер максимальной клики в таком графе должен быть порядка 2log₂N. Это доказывается неконструктивным образом, то есть доказательство этого факта показывает, что клика такого размера с вероятностью, стремящейся к 1, должна существовать в достаточно большом графе, но не показывает, как эту клику найти. В то же время, типичный полиномиально быстрый алгоритм – например, алгоритм Карпа – находит клику лишь с максимальным размером порядка log₂N.
Как видно, существует разрыв между типичным оптимумом log₂N, даваемым быстрым алгоритмом, и типичным глобальным оптимумом задачи 2log₂N, причем этот разрыв существенен: с ростом размера задачи N он лишь увеличивается. Это свидетельствует о том, что быстрый алгоритм, как правило, ведет нас отнюдь не в те области конфигурационного пространства, где находятся близкие к оптимальному решения.
#стекла #оптимизация
Действительно, многие быстрые алгоритмы полиномиальной трудоемкости являются стабильными: то есть даваемые ими решения задачи слабо меняются при слабых изменениях условии задачи (например, при удалении единственного ребра большого графа, в котором нужно найти максимальную клику). Кластеризация же решений задачи, вытекающая из существования щели между перекрытиями, говорит о том, что не только наилучшее (тот самый единственный глобальный минимум функции потерь), но и близкие к наилучшему решения могут резко и непредсказуемо меняться при изменении условий задачи. Быстрый эвристический алгоритм, попадающий в кластер почти оптимальных решений и потому дающий хороший результат на одном экземпляре задачи, может дать куда худший результат при слегка измененных условиях задачи – потому что этот кластер может уже стать сильно неоптимальным.
С этим свойством, вероятно, связано и наблюдающийся в некоторых оптимизационных задачах существенный разрыв между типичным и алгоритмическим оптимумами. Что это такое, можно понять на примере задачи поиска максимальной клики (подмножества узлов, которые все попарно соединены между собой) в случайном графе Эрдёша-Реньи, где любые два узла соединены или не соединены ребром с вероятностью 1/2. Известно, что при общем числе узлов N >> 1 типичный размер максимальной клики в таком графе должен быть порядка 2log₂N. Это доказывается неконструктивным образом, то есть доказательство этого факта показывает, что клика такого размера с вероятностью, стремящейся к 1, должна существовать в достаточно большом графе, но не показывает, как эту клику найти. В то же время, типичный полиномиально быстрый алгоритм – например, алгоритм Карпа – находит клику лишь с максимальным размером порядка log₂N.
Как видно, существует разрыв между типичным оптимумом log₂N, даваемым быстрым алгоритмом, и типичным глобальным оптимумом задачи 2log₂N, причем этот разрыв существенен: с ростом размера задачи N он лишь увеличивается. Это свидетельствует о том, что быстрый алгоритм, как правило, ведет нас отнюдь не в те области конфигурационного пространства, где находятся близкие к оптимальному решения.
#стекла #оптимизация
PNAS
The overlap gap property: A topological barrier to optimizing over random structures | Proceedings of the National Academy of Sciences
The problem of optimizing over random structures emerges in many areas of science
and engineering, ranging from statistical physics to machine lear...
and engineering, ranging from statistical physics to machine lear...