Вот пара примеров, демонстрирующих возникновение асимптотики функции распределения p(s) ≈ exp(–nI(s)), описываемой теорией больших отклонений.

Функцию Крамера I(s) можно определить как предел функции –(1/n)ln p(s) при n → ∞. На графиках сверху показано, как ведут себя плотности распределения p(s) среднего арифметического n одинаковых гауссовых случайных величин и полученные из них комбинации –(1/n)ln p(s). Видно, что последние стремятся к конечному пределу – параболе I(s) = (s–1)²/2, которая и является функцией Крамера. Хотя сами функции распределения p(s) продолжают меняться при увеличении n, становясь все более острыми, их поведение можно описать универсальной асимптотикой.

На графиках снизу показано то же самое для распределения Бернулли, где с вероятностями α и 1– α выпадают 1 или 0. В пределе n → ∞ среднее арифметическое всех n выпавших величин становится непрерывной величиной, описываемой функцией Крамера I(s) = s ln(s/α) + (1 – s)ln[(1 – s)/(1 – α)].

#математика #стохастическая_термодинамика

Универсальная фраза, которую можно добавить в любую статью.

#цитаты

А вот статья с довольно математизированным описанием применений теории больших отклонений в статистической физике. Основной посыл статьи в том, что возможны три уровня описания статистических систем, перекочевывающие и в теорию больших отклонений.

1-й уровень описания – это расчет средних по статистическому ансамблю значений наблюдаемых величин. Теория больших отклонений на этом уровне дает информацию о том, как именно и с какой скоростью флуктуирующие значения наблюдаемых сосредотачиваются вокруг своих средних при росте числа частиц, объема или с ростом времени – по мере того, как система стремится к термодинамическому равновесию.

2-й уровень описания – рассмотрение всего статистического распределения случайной величины. Теория больших отклонений показывает здесь, как распределение стремится к своей предельной форме – например, к распределению Гиббса для энергии или к гауссовому распределению для флуктуаций параметра порядка. Здесь возникают такие величины, как расхождение Кульбака-Лейблера, энтропия Шеннона и другие величины, сближающие статистическую физику с теорией информации.

Наконец, 3-й уровень описания – это распределение траекторий системы, то есть не просто статистического ансамбля, а его эволюции с течением времени. Здесь теория больших отклонений позволяет исследовать общие закономерности поведения системы с течением времени. Например, хаотическую динамику, обусловленную ростом энтропии Колмогорова-Синая.

#стохастическая_термодинамика #термодинамика

«Продемонстрировать, что статистическая система действительно подчиняется принципу больших отклонений – это очень сложная задача (особенно для физиков)»

#цитаты #стохастическая_термодинамика

Теорема Санова проводит интересную связь между расхождением Кульбака-Лейблера и теорией больших отклонений.

Представим, что мы N раз подряд выбрасываем одну и ту же случайную величину, описываемую априорным распределением вероятностей {qᵢ}. Подсчитывая, в какой доле испытаний у нас выпало каждое значение i в реальности, мы получаем эмпирическое распределение вероятностей {pᵢ}.

Мы знаем, что в пределе большого числа испытаний N → ∞ эмпирические вероятности должны сходиться к априорным. Но с какой скоростью это будет происходить? На этот вопрос отвечает теорема Санова: она утверждает, что вероятность получить эмпирические частоты {pᵢ} при большом числе испытаний N в главном (экспоненциальном по N) порядке ведет себя как exp{–ND(p|q)}, где D(p|q) = ∑ᵢpᵢln(pᵢ/qᵢ) – расхождение Кульбака-Лейблера между распределениями {pᵢ} и {qᵢ}.

Как видно, это формулировка, типичная для теории больших отклонений. В пределе N → ∞ ненулевая вероятность остается только у варианта pᵢ = qᵢ, для которого D(p|q) = 0. Это закон больших чисел: при наборе большой статистике эмпирические частоты стремятся к априорным. Но теорема Санова позволяет легко оценить и отклонения от закона больших чисел: например, можно в одну строчку, без громоздкого подсчета числа комбинаций, оценить, какова (по порядку величины) вероятность выпадения 48 орлов и 52 решек при 100 бросаниях монеты.

Отсюда же виден и статистический смысл расхождения Кульбака-Лейблера D(p|q): оно показывает, насколько маловероятно в реальности отклонение реальных частот {pᵢ} от идеальных {qᵢ}, получаемых лишь в пределе N →∞. Это согласуется и с информационным смыслом расхождения Кульбака-Лейблера: оно показывает, какое количество информации мы теряем при аппроксимации правильного статистического распределения {qᵢ} приближенным распределением {pᵢ}.

#математика #объяснения #информация

Любопытное теоретическое предсказание спонтанного образования вихрей в экситон-поляритонном бозе-конденсате, вращающихся по кругу подобно часовой стрелке. Для этого полупроводниковую квантовую яму нужно подвергать нерезонансной накачке лазерным лучом, имеющим C-образную форму и создающим для поляритонов такой же формы отталкивающий потенциал.

На рисунке показаны два стабильных состояния, образующихся при такой накачке. В первом состоянии (возникающем в определенном диапазоне мощностей накачки) один из квантованных вихрей находится внутри буквы C, а другой бегает по ее внешнему периметру с почти постоянной угловой скоростью. Во втором состоянии (при больших мощностях накачки) по периметру бегают уже два вихря, находящиеся в диаметрально противоположных точках.

Авторы предполагают, что таким образом можно создавать тактовые генераторы, работающие на частотах в десятки гигагерц и требующие сравнительно небольшой мощности для своей работы.

#поляритоны #бозе_конденсация

Недавний эксперимент, в котором наблюдали идеальный эффект увлечения электронов в двумерном MoSe₂ дырками в WSe₂, обусловленный межслойным экситонным спариванием.

На диаграммах в центре показано, что при определенных комбинациях затворных напряжений V_b и V_g существует pn-область, в которой полупроводниковый слой MoSe₂ допирован электронами, а слой WSe₂ допирован дырками. В небольшой части этой области, где концентрации электронов и дырок почти равны, система является несжимаемой (левая диаграмма для емкости), а в верхнем слое возникает электрический ток увлечения I_drag, обусловленный пропусканием тока I_drive через нижний слой.

Как видно на графике снизу, в этой области наблюдается идеальное увлечение электронов в одном слое дырками в другом слое: токи I_drive и I_drag равны по величине и противоположны по направлениям. Причина этого – в связывании электронов и дырок в межслойные экситоны, возникающем при температурах ниже 20 К.

#экситоны #дихалькогениды_переходных_металлов

Эпистемологическая, или психологическая стрела времени заключается в том, что мы помним события прошлого, но не способны точно так же «вспоминать» будущее – хотя, казалось бы, законы физики, управляющие поведением нашего мозга, должны работать одинаково при обоих направлениях течения времени. То же самое касается и других систем, работающих в качестве памяти – бумаги с надписями и рисунками, жестких дисков, картин и даже лунных кратеров, хранящих «память» о прошлых попаданиях метеоритов. Все эти системы работают во времени лишь в одну сторону. В принципе, иногда мы можем «вспоминать» события будущего – то есть делать прогнозы – но это дело гораздо более сложное и, как правило, требующее гораздо больших вычислительных ресурсов, чем восстановление событий прошлого.

Самое распространенное объяснение эпистемологической стрелы времени сводит ее к космологической стреле времени – общей направленности большинства процессов в нашей Вселенной от более упорядоченных состояний в прошлом к более разупорядоченным состояниям в будущем, сопровождающихся ростом энтропии. Проще всего это понять на примере лунных кратеров: наблюдая поверхность Луны в текущий момент времени t₀ и видя на ней неровность в форме кратера, мы заключаем, что в какой-то предшествующий момент времени t₁ < t₀ произошло столкновение Луны с метеоритом. Для формулировки такого вывода мы привлекаем дополнительную информацию: знание определенных законов природы, знания о том, что такое метеориты и т.д.

Почему мы уверены, что удар метеорита произошел именно в предшествующий момент времени, а не произойдет в будущем? Откуда возникает временная асимметрия работы поверхности Луны как устройства памяти? Потому что мы уверены, что в еще более отдаленный момент прошлого t₂ < t₁ поверхность Луны была ровной. А сами собой неровности на ней не возникают (здесь, опять-таки, привлекается знание симметричных во времени законов природы) – поэтому где-то в момент времени t₁, лежащий между моментами t₂ и t₀, должен был произойти удар метеорита, память о котором и хранится. Тот факт, что t₂ < t₀, делает лунный кратер примером памяти о событии прошлого.

В принципе, можно представить себе другую ситуацию: допустим, мы уверены, что в какой-то момент t₂ > t₀ в будущем поверхность Луны будет ровной, а в текущий момент времени t₀ видим на ней кратер. Зная законы природы, мы можем сделать вывод, что где-то в будущем, между моментами t₀ и t₂ (в промежуточный момент времени t₀ < t₁ < t₂) произойдет что-то, выравнивающее поверхность Луны: например, на нее упадет метеорит, уничтожающий кратер. Как видно, при t₂ > t₀, лунные кратеры становятся уже не памятью о событиях прошлого, а свидетельством событий, которые обязательно произойдут в будущем.

Таким образом, асимметрия работы поверхности Луны как устройства памяти сводится к вопросу о том, почему мы уверены в том, что эта поверхность была ровной именно в отдаленном прошлом, а не будет такой в отдаленном будущем. А это уже проявление общей направленности космологической эволюции: мы знаем, что Луна образовалась из расплавленных горных пород, которые при остывании сформировали ровный шар. А ровным он оказался из-за затухания волн, бегавших по его жидкой поверхности, которые передали свою энергию теплу, рассеявшемуся в дальнейшем в космическое пространство. Это процесс, сопровождавшийся ростом энтропии и протекавший вполне естественно при тогдашнем (да и нынешнем тоже) состоянии Вселенной. Если бы эволюция Вселенной шла как-то иначе – например, космическое пространство было бы не холодным и пустым, а нагретым и плотно заполненным веществом, – то ровная поверхность Луны вряд ли могла бы сформироваться.

Хотя мы не знаем пока во всех деталях, как именно формируются воспоминания, хранимые нашим мозгом, можно предположить, что механизм возникновения асимметрии времени здесь похожий. Наш мозг, как биологическая система, потребляет питательные вещества и выделяет тепло – то есть постоянно увеличивает энтропию Вселенной, приготавливая «выровненные» состояния, готовые к записи воспоминаний.

#популярное #объяснения

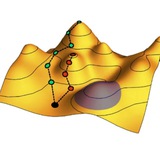
Кстати говоря, объяснения того, как эпистемологическая стрела времени связана с общей направленностью эволюции нашей Вселенной в сторону увеличения энтропии, можно наглядно представить в терминах ветвящейся структуры.

Рост энтропии – то есть нарастание степени нашего незнания о точном состоянии системы – состоит в разбрасывании состояний системы по все большему и большему числу различных вариантов с течением времени. К примеру, координаты молекул газа, необратимо разлетевшегося в пустоту, имеют гораздо большую степень неопределенности, чем когда он был в сосуде.

Представим, что мы находимся в определенной точке древовидной структуры всех предельно конкретных (но неизвестных нам доподлинно) состояний Вселенной. Тогда, зная симметричные во времени законы природы (определенным образом стыкующие ветви между собой), мы можем сказать гораздо больше определенного о предшествующих состояниях Вселенной (лежащих выше ветвях), чем о будущем.

#популярное #объяснения

Авторы этой статьи сделали попытку описать возникновение эпистемологической стрелы времени на формально-математическом уровне. Они вводят три типа устройств, которые могут функционировать в качестве памяти, отличающиеся ролью, которую играет состояние самой памяти и части окружающего ее мира для восстановления информации о прошлом (или о будущем).

Память 1-го типа позволяет сделать выводы о состоянии окружающего мира w₁ в момент времени t₁ на основе знания о состоянии памяти m₀ в текущий момент времени t₀. Фраза «позволяет сделать выводы» означает большую величину взаимной информации между статистическими распределениями состояний w₁ и m₀. Это, в принципе, интуитивно понятно: наблюдая определенные состояния памяти в данный момент времени, мы сразу же делаем вывод о том, каково вероятное состояние окружающего мира в другой момент времени.

Память 2-го типа отличается тем, что для получения выводов о состоянии окружающего мира w₁ нам нужно знать не только текущее состояние памяти m₀, но и быть уверенными в том, что текущее состояние окружающего мира w₀ попадает в определенное подмножество состояний. Пример такой памяти появляется в компьютерах. Если мы знаем, что компьютер выполняет определенную программу (программа – это состояние w₀ части окружающего мира, внешней по отношению к памяти), то текущее состояние памяти позволяет понять, какими являются состояния компьютера в другие моменты времени. Примечательно, что память 2-го типа симметрична во времени: зная устройство программы, мы по текущему состоянию компьютерной памяти можем восстановить ход вычислений как в направлении прошлого, так и в направлении будущего. Еще пример памяти 2-го типа – Солнечная система, тоже эволюционирующая по «запрограммированным» законам небесной механики, где по текущему положению планет, их спутников и астероидов мы можем восстановить их положения как в прошлые моменты времени, так и в будущее.

Что же касается памяти 1-го типа, то единственная ее разновидность, которая реально может работать как память – это особый случай, который авторы называют памятью 3-го типа. Она отличается наложением дополнительных условий на состояние памяти m₁ в момент времени t₁ – тот самый момент, когда окружающий мир еще не провзаимодействовал с нашей памятью (взаимодействие произойдет в какой-то другой момент времени, промежуточный между t₁ и t₀). Если вспомнить лунные кратеры как пример памяти, то дополнительное условие состоит в том, что поверхность Луны в момент времени t₁ должна быть ровной – тогда наличие кратера (состояние «памяти») в текущий момент времени t₀ свидетельствует о взаимодействии Луны с метеоритом («окружающем миром») в момент времени, лежащий между t₁ и t₀.

Я не совсем понял смысл математических условий, наложенных на состояние памяти m₁, но в общих чертах они сводятся к тому, что состояние m₁ должно быть приготовлено в процессе сокращения числа состояний (state space collapse), превращающего более широкое множество состояний памяти в более узкое множество. По сути, это процесс инициализации памяти, приведения ее в «стертое» состояние, готовое к записи новой информации. Применительно к поверхности Луны это ее выравнивание: множество различных неровных конфигураций превращаются в единственную ровную. Как известно из термодинамики, процесс сокращения числа состояний памяти (то есть уменьшения ее энтропии) должен сопровождаться ростом энтропии остальной части Вселенной.

Таким образом, память 3-го типа может работать только в том случае, если ее «исходное» состояние в момент времени t₁ было приготовлено в ходе процесса, увеличивающего энтропию Вселенной. Это приводит к определенной направленности работы памяти – той самой эпистемологической стреле времени. Если процессы увеличения энтропии Вселенной идут преимущественно в одном направлении – в сторону увеличения переменной t, – то и память 3-го типа будет работать тоже лишь в этом направлении.

#популярное #объяснения #информация #термодинамика

В этой работе теоретически рассмотрены поверхностные плазмоны на графене, помещенном между двумя диэлектрическими средами, одна из которых пассивна (обладает диссипацией, Im ε > 0), а другая активна (обладает противоположной по знаку Im ε). Если сам графен не имеет диссипации, то вся система оказывается PT-симметричной, потому что ее активные и пассивные области меняются местами при пространственной инверсии.

Неэрмитовы PT-симметричные системы примечательны своими исключительными точками в пространстве параметров, где два чисто вещественных значения энергии смыкаются и превращаются в два комплексно сопряженных. Аналог этого явления виден и на графиках для вещественной kₓ´ и мнимой kₓ´´ частей волнового вектора как функции частоты ω: по мере роста ω два комплексно сопряженных волновых вектора kₓ (точки C и D) превращаются в два чисто вещественных (A и B), а затем снова в два комплексно сопряженных (E и F). Таким образом, на оси ω мы наблюдаем две исключительные точки.

#неэрмитовы_системы #графен #плазмоны

Предел Либа-Робинсона – это один из квантовых пределов скорости, налагающих ограничения на скорости, с которыми квантовые системы могут менять свои состояния.

Как известно, в одномерной цепочке, где частицы могут перескакивать между соседними узлами, разделенными расстоянием a, с интегралом перескока J, дисперсия волн имеет вид E(k) = –2J cos(ka). Это означает, что групповая скорость возбуждений ∂E/ħ∂k = (2Ja/ħ)sin(ka) в такой системе не может превышать верхний предел 2Ja/ħ. Следовательно, любые сигналы не могут распространяться по цепочке быстрее некоторой предельной скорости, равной Ja/ħ по порядку величины– это и есть предел Либа-Робинсона.

В этой статье дается обзор всевозможных разновидностей пределов скорости для квантовых многочастичных систем: для распространения энергии, информации, квантовой запутанности и других корреляций. Примечательно, что они могут применяться и в статических задачах, давая, например, ограничения на протяженность квантовой запутанности в пространстве.

#квантовая_механика

Любопытная работа, где предсказывается кооперативное усиление мощности и эффективности работы тепловой машины, состоящей из двух гармонических осцилляторов, взаимодействующих с одними и теми же термостатами.

Термостаты описываются моделью Кальдейры-Леггетта (это система большого числа невзаимодействующих осцилляторов), а цикл работы тепловой машины задается периодическими модуляциями силы связи обоих осцилляторов, составляющих рабочее тело, с горячим термостатом. Если приближенно исключить термостаты, динамика осцилляторов описывается системой уравнений, связанных диссипативным членом γ₂ через термостаты (прямая связь между осцилляторами отсутствует). В такой системе возникает коллективная мода, затухание которой парадоксальным образом исчезает в пределе сильной диссипации γ₂ → ∞.

Именно благодаря ей мощность тепловой машины при больших γ₂ оказывается гораздо выше, чем в случае совокупности двух независимых тепловых машин, как показано на рисунке сравнением красных и синих точек.

#квантовая_термодинамика

А вот еще картинка из статьи из предыдущего поста: здесь для изученной тепловой машины авторы находили фронт Парето в пространстве выделяемой ей мощности P и КПД ее работы η.

Фронтом Парето называется множество таких точек в пространстве характеристик системы, где для увеличения одной из них обязательно придется уменьшить другую. То есть это множество оптимальных комбинаций, демонстрирующих пределы эффективности, за которые уже не перешагнуть.

На рисунке показаны положения фронта Парето на плоскости (η, P) при разных отношениях частот двух осцилляторов. Каждая точка фронта, демонстрирующая компромисс между мощностью и КПД, была получена оптимизацией по всем возможным циклам, то есть всем возможным периодическим зависимостям сил связи каждого осциллятора с каждым термостатом от времени. Можно видеть, что в случае кооперативной системы (синие точки) фронт Парето продвигается значительно дальше, чем в случае системы двух отдельных, несвязанных осцилляторов (оранжевые точки).

#квантовая_термодинамика

Формула Онзагера-Мэчлапа (Onsager-Machlup formula) – это некий аналог фейнмановского интеграла по путям, только для процесса классической диффузии частиц, или броуновского движения.

Рассмотрим безынерционное (overdamped) движение частицы, описываемое уравнением Ланжевена, показанным на рисунке сверху. На частицу действует зависящая от координат сила F (не обязательно потенциальная) и зависящая от времени сила случайного шума, масштабированная на коэффициент диффузии D. Тогда вероятность реализации пути r(t) будет задаваться интегралом вдоль этого пути, показанным внизу.

Первое слагаемое в экспоненте заставляет частицу двигаться со скоростью вдоль силы F и штрафует за отклонения – тем слабее, чем больше коэффициент диффузии D. Второе слагаемое штрафует путь (делает его менее вероятным) за посещение областей с положительной дивергенцией F, потому что div F > 0 означает, что сила F выталкивает частицу из такой области наружу.

#стохастическая_термодинамика #объяснения

Стильно выглядящая солнечная батарея: она изготовлена с использованием так называемого черного кремния: обычного кремния, поверхность которого покрыта массивом кремниевых же наночастиц. Образующаяся метаповерхность хорошо поглощает свет в значительной части видимого диапазона.

#фотоника

А это – в представлении художника – плазмоэлектрический эффект: возникновение разности потенциалов при облучении светом метаповерхности с массивом отверстий в металле, обусловленное возбуждением плазмонов.

#плазмоны

Изобретение долгой краткосрочной памяти (long short-term memory), сделанное в 1997 году, произвело настоящую революцию в практике создания рекуррентных нейронных сетей, работающих с длинными последовательностями сигналов: текстами, речью и другими звуками, видеопотоками и т.д.

В отличие от сетей прямого распространения (feedforward network), через которую сигналы проходят только один раз и в одну сторону от входа к выходу, рекуррентная нейронная сеть допускает распространение сигналов в любые стороны, как в человеческом мозге. Так можно заставлять нейросеть обрабатывать входные данные, которые не имеют определенной размерности (как, например, единственная пиксельная картинка, которую нужно распознать), а последовательно поступают в течение длительного времени. Простейшая организация нейросети для такой задачи – это замыкание ее в цикл, когда выходные сигналы h нейросети подаются обратно на ее вход вместе со входными данными x. Тогда на каждом шаге времени t нейронная сеть будет обрабатывать совокупность входных данных x(t) и выходных данных h(t–1) – результатов «переваривания» всех предшествующих входных данных x(t–1), x(t–2) и т.д., формируя новые выходные данные h(t) = f(x(t), h(t–1)), которые на следующем шаге снова поступят на ее вход.

Проблема такого подхода в сложности обучения получившейся сети. Для подгонки параметров сети w – весов межнейронных связей и смещений – с целью уменьшения функции ошибок L нужно вычислять градиент ∂L/∂w. Это делается при помощи алгоритма обратного распространения ошибки: вектор величины ошибок последовательно прогоняется от выходного слоя нейронов к входному задом наперед, на каждом шаге умножаясь на некие матрицы. В случае описанной выше рекуррентной архитектуры этот проход через нейросеть задом наперед нужно повторять множество раз – точно так же, как при работе сети сами сигналы многократно проходят через одну и ту же последовательность нейронных слоев. Фактически получается умножение вектора ошибок на одну и ту же совокупность матриц M, возведенную в большую степень: а это приводит к тому, что ошибки либо улетают на бесконечность (если мы попали на собственный вектор M с собственным значением больше 1), либо экспоненциально падают почти до нуля (если собственное значение меньше 1). Это называется проблемой взрывающихся градиентов и проблемой исчезающих градиентов.

Долгая краткосрочная память позволяет решить эту проблему путем распутывания сигналов данных и сигналов ошибок. Этот метод основан на включении в нейронную сеть ячеек памяти, входы и выходы которых связаны с остальными слоями нейронов мультипликативными вентилями – операциями поэлементного умножения. А именно:
– Вектор значений c(t) в ячейках памяти частично складывается из входного сигнала i(t), умноженного поэлементно на значения входного вентиля g(t).
– Другая часть вектора c(t) формируется старым содержимым памяти c(t–1), умноженным на значения вентиля забывания f(t).
– На выход ячейки памяти – который, в простейшем случае, дает выходной сигнал h(t) всей сети – подается ее содержимое c(t), умноженное на значение выходного вентиля o(t).
При этом все значения на вентилях g(t), f(t), o(t) вычисляются отдельными слоями нейронов, на основе сигналов x(t) и h(t–1), поступающих на вход всей сети.

При вычислении градиента функции ошибок в такой архитектуре сети некоторые производные искусственно зануляются: а именно, считается, что ошибки сигналов на выходе каждого мультипликативного вентиля обусловлены только ошибками значения самого вентиля (g(t), f(t) либо o(t)), а не того входного сигнала, который на него умножается. Это позволяет избежать проблемы взрывающихся и исчезающих градиентов, потому что бесконечный цикл прохода ошибок по одним и тем же слоям нейронов размыкается. Создается так называемая «карусель ошибок», при которой ошибка продолжает циркулировать внутри ячейки памяти и через вентили, но ее величина остается стабильной. По крайней мере, так я понял довольно тяжеловесные объяснения авторов оригинальной работы.

#нейронные_сети #объяснения #популярное

А вот картинка и формулы, иллюстрирующие работу долгой краткосрочной памяти, которая на словах описывалась в предыдущем посте.

Каждый кружочек g, f, o – это слой нейронов, на который подаются входные данные x, поступившие на текущем временном шаге, и выходные данные h с предыдущего шага. Так формируются значения вентилей от 0 до 1, которые поэлементно умножаются (крестики) на другие сигналы: обработанный входной сигнал i, а также значения c ячейки памяти, поступающие как на выход сети (вправо), так и обратно в память (снизу).

Вентили позволяют нейросети управляемым образом открывать ячейку памяти для записи новых значений (через входной вентиль g), сохранять значения в памяти либо стирать их (через вентиль забывания f) и выводить значения из памяти наружу (выходной вентиль o). Таким образом, сеть может долгое время удерживать в памяти результаты обработки данных, поступивших ей на вход давным-давно, если они вдруг понадобятся, «срезонировав» с текущими данными.

#нейронные_сети #объяснения #популярное

А вот некоторые результаты, которые изобретатели долгой краткосрочной памяти – Зепп Хохрайтер и Юрген Шмидхубер – сразу же продемонстрировали на практике.

▪️ Нейросеть в виде ячейки долгой краткосрочной памяти заставляли предсказывать следующую букву грамматики Ребера по предшествующим буквам. Здесь не требуется долгое удержание значений в памяти, поскольку грамматика Ребера содержит лишь близкие корреляции, но это популярная модель для тестирования методов машинного обучения. Новая нейросеть успешно справилась с задачей угадывая символы более чем в 97% случаях, в отличие от других рекуррентных архитектур.

▪️ Наборы символов, разделенные длинными последовательностями: нейросеть учат распознавать последовательности символов вида (x … x), (y … y), (e, x … e, x), (b, y … b, y), где многоточия обозначают несколько сотен «отвлекающих» символов – либо каждый раз одних и тех же, либо случайно меняющихся. Нейросеть должна сопоставить символы в самом начале последовательности с символами в самом ее конце, проигнорировав все промежуточные. Это значит, что начальные символы она должна очень долго удерживать в памяти. Новая архитектура отлично справилась с этими задачами на 100%, в то время как другие варианты сетей справлялись с ними лишь с вероятностью успеха 22-78%, а некоторые вообще не справились.

▪️ Задачи условного сложения и умножения, которые никогда раньше не решались рекуррентными сетями: на вход подается последовательность пар чисел (xᵢ, yᵢ), и нейросеть должна посчитать либо сумму всех xᵢ, либо произведение всех xᵢ, для которых yᵢ = 1. Как видно, здесь требуются весьма нетривиальные операции с комбинациями входных чисел и содержимым памяти.

#нейронные_сети #популярное

В этой работе сотрудников Google 2014 года долгая краткосрочная память использовалась для машинного перевода предложений с английского языка на французский. В принципе, ответы на вопросы – это похожая по структуре задача, где последовательности входных слов нужно сопоставить последовательность выходных слов. Так что эту работу можно считать ранней стадией разработки нейросети ChatGPT.

Архитектура нейросети довольно простая: она состоит из двух ячеек долгой краткосрочной памяти, хотя и не простой, а так называемой глубокой памяти: внутри ячейки сигналы проходят через 4 слоя по 1000 нейронов каждый. Размерность сигнала 1000 отвечает размерности пространства, на которое отображается каждое из слов английского и французского языков. На первую ячейку памяти подается исходное предложение на английском, та ее переваривает и выдает окончательный сигнал – «скрытое представление» предложения, содержащее его смысл в виде вектора в 1000-мерном пространстве. Этот сигнал затем поступает на вторую ячейку памяти, которая, циклически работая, выдает переведенное предложение на английском – слово за словом, пока не выдаст специальный символ конца предложения. Долгая краткосрочная память особенно удобна здесь тем, что она может работать с последовательностями слов произвольной длины.

Построенная модель показала в целом заметно лучшие результаты, чем другие методы машинного перевода. Интересно, что результаты получились гораздо лучше при обращении порядка слов во входном предложении: если подавать на нейросеть последовательность CBA вместо исходной последовательности слов ABC, то ей легче связывать слово A, которое окажется последним на входе, с его переведенным аналогом, который окажется на выходе первым и т.д.

#нейронные_сети #популярное