Кинетическое уравнение Больцмана для частиц в сферически-симметричном гармоническом потенциале предсказывает существование монопольной «дышащей» моды: периодического расширения и сжатия системы частиц, происходящего полностью изотропно. Интересно, что такая мода не затухает, несмотря на наличие столкновений между частицами, которые, казалось бы, должны вести систему к состоянию теплового распределения.

В этом эксперименте монопольная мода наблюдалась в газе атомов рубидия, помещенных в очень ровную гармоническую ловушку. На графиках показаны измеренные колебания монопольной и, для сравнения, квадрупольной моды. Видно, что монопольная мода действительно практически на затухает: время ее жизни около 30 секунд, в то время как квадрупольная мода затухает примерно за 1 секунду.

Остаточное затухание обусловлено, как считают авторы, слабой анизотропией ловушки в районе 0.05%, из-за которой монопольная мода связывается с короткоживущей квадрупольной и отдает ей свою энергию.

#атомные_газы #термодинамика

Действительно, давайте найдем эффективную эффективность тепловой машины.

#стохастическая_термодинамика #цитаты

Гильбертово пространство состояний квантовой системы очень обширно. Те состояния системы, которые в принципе могут нам встретиться в любой реалистичной физической задаче, занимают лишь небольшой его уголок, который называют physical corner.

Вот работа, в которой это иллюстрируется. Авторы показывают, что если мы возьмем квантовую систему в некотором «референсном» состоянии (это может быть основное состояние, вакуум или ферромагнетик) и начнем подвергать ее эволюции под действием локального гамильтониана в течение времени, полиномиального по размеру системы, то множество состояний, которые система сможет таким образом достичь, будет занимать лишь экспоненциально малую долю всего гильбертова пространства. Здесь предполагается, что гамильтониан является k-локальным (то есть состоит из слагаемых, каждое из которых действует на степени свободы не более чем k частиц), а спектр его энергий ограничен.

С малостью объема физического угла связан успех теоретических методов, описывающих волновые функции квантовых многочастичных систем при помощи относительно простых анзацев – определителей Слэтера, вариационных функций БКШ, матричных и тензорных произведений и т.д.

Стоит отметить, что «классические» состояния любой квантовой системы, которые отвечают ее состояниям, наблюдаемым нами в повседневной жизни, занимают еще меньшую долю гильбертова пространства – так называемый классический домен. Он окружен небольшим квантовым гало – теми неклассическими состояниями, до которых мы можем дотянуться своими экспериментами.

#квантовая_механика

А вот интересная формула из статьи из предыдущего поста. Она ограничивает сверху различие между результатом хронологически упорядоченной эволюции в течение небольшого промежутка времени Δt и такой же эволюции, но без хронологического упорядочения T.

Различие между ними ограничивается максимальной нормой гамильтониана за весь промежуток времени и самим этим промежутком времени. Напомню, что норма ||A|| оператора A – это максимальный модуль его матричных элементов |<φ|A|ψ>| по всем нормированным на единицу векторам |φ> и |ψ > гильбертова пространства.

Физический смысл этой формулы в том, что можно пренебречь флуктуацями гамильтониана на малых промежутках времен, из за которых гамильтониан в разные моменты времени не коммутирует сам с собой, так что его операторную экспоненту приходится хронологически упорядочивать.

#квантовая_механика

Стрелой времени называют преимущественную направленность множества наблюдаемых физических процессов во времени: тепло переходит от горячих тел к холодным, а не наоборот, открытая квантовая система теряет свою когерентность, запутываясь с окружением, наш мозг помнит события прошлого, но не «помнит» будущее и т.д.

В этой работе демонстрируется и экспериментально проверяется соотношение между средним производством энтропии <Σ>, происходящей в квантовой системе за время от 0 до τ, с асимметрией ее динамики во времени – той самой стрелой времени. Это соотношение выглядит как <Σ> = S(ρ^F(t) | ρ^B(τ–t)), где S – расхождение Кульбака-Лейблера между двумя матрицами плотности, ρ^F(t) – матрица плотности системы, начинающей свою эволюцию с равновесного состояния в момент времени 0 до любого промежуточного момента времени t, а ρ^B(τ–t) – матрица плотности системы, эволюционирующей обратно во времени с момента τ до текущего момента t.

Таким образом, производство энтропии <Σ> – термодинамическая мера необратимости процесса, пропорциональная энергии T<Σ>, переходящей в тепло, – связывается с информационной мерой необратимости этого процесса – а именно, с мерой того, насколько сильно нарушается симметрия эволюции системы во времени. В отсутствие стрелы времени прямая эволюция системы от 0 до t давала бы ровно такой же результат, как и обратная эволюция от τ до t, тогда расхождение Кульбака-Лейблера между двумя матрицами плотности было бы равно нулю, и диссипация энергии тоже отсутствовала бы.

#термодинамика #квантовая_термодинамика

А вот результаты эксперимента по проверке связи между стрелой времени – необратимостью эволюции квантовой системы – и производством энтропии.

Квантовой системой служил кубит, построенный на двух ориентациях ядерного спина ¹³C в молекуле хлороформа. Эволюция кубита вперед (от 0 до τ) назад (от τ до 0) во времени начиналась с равновесных состояниях и шла под действием противоположных во времени изменений его гамильтониана, реализуемых его облучением микроволнами.

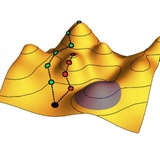
Диаграмма снизу показывает, как при этом меняется вектор состояния кубита на блоховской сфере: по мере того, как в ходе прямой и обратной эволюции вектор гамильтониана движется вдоль одной и той же зеленой линии, но в обратных направлениях, векторы состояния отходят от этой линии из-за неравновесности динамики, причем по-разному при разных ее направлениях. На графике показано подтверждение связи между производством энтропии <Σ> и асимметрией матриц плотности, справедливой по все моменты времени t от 0 до τ.

#термодинамика #квантовая_термодинамика

В этой теоретической работе было предсказано существование экситонов с линейной дисперсией в двумерных дихалькогенидах переходных металлов: зависимость их энергии от импульса центра масс электрона и дырки напоминает световой конус. Как показано на графике сверху, в MoS₂ существуют не только безмассовые внутридолинные экситоны, но и две ветви массивных экситонов, расщепленные по спину.

Возникновение линейного по импульсу Q вклада в энергию экситона объясняется обменным взаимодействием: процессом виртуальной аннигиляции электрона и дырки, добавляющей к энергии слагаемое ΔE ~ |<ex(Q)|p|0>|²v(Q), где v(Q) = 2πe²/Q – двумерное кулоновское взаимодействие, <ex(Q)|p|0> ~ Q – матричный элемент аннигиляции экситона (его превращения в вакуум), которая запрещена правилами отбора ровно в дираковской точке Q = 0, но становится разрешенной при Q ≠ 0. В итоге получается неаналитическая зависимость ΔE ~ |Q| энергии от импульса.

#экситоны #дихалькогениды_переходных_металлов

Большая статья – или «дорожная карта», состоящая из небольших текстов нескольких десятков авторов, работающих в области магноники. Это всевозможные манипуляции с магнонами, то есть спиновыми волнами в магнетиках, направленные на создание аналогов классических электронных устройств или квантово-вычислительных систем.

Магноны сочетают в себе гигагерцовые частоты с нанометровыми длинами волн, а также хорошо взаимодействуют с электромагнитными полями, что весьма хорошо с точки зрения практических применений. Сейчас с магнонами чего только не делают: всевозможные наноструктуры, резонаторы, магнонные кристаллы, метаматериалы, волноводы, соединители, логические элементы, а также гибридные квантовые устройства, в которых магноны связываются со сверхпроводниковыми кубитами и резонаторами.

Большая часть всех этих задумок пока остаются на уровне теории, но и экспериментов тоже немало: в последнее время публикуется более 600 статей в год, посвященных магнонам.

#магнетизм

А вот интересный пример из обзора по магнонике. Мы пытаемся перевести спиновую волну из одного магнонного волновода в другой, используя в качестве посредника промежуточный волновод. Для этого участки волноводов сближаются, так что возбуждение передается через ближнее магнитное поле.

Такая передача через посредника похожа на STIRAP (стимулированный рамановский перенос) в физике электромагнитно-индуцированной прозрачности: меняя расстройки в схеме с Λ-резонансом, мы перекачиваем систему из левого состояния в правое в виде последовательности двух дипольных переходов, когда прямой переход запрещен правилами отбора.

Интересно, что «интуитивное» устройство системы, при котором сближаются сначала 1-й (передающий сигнал) и 2-й (промежуточный) волноводы, а потом 2-й и 3-й (принимающий), работает гораздо хуже, чем «контринтуитивное», где все наоборот. Как видно, во втором случае промежуточный волновод почти не возбуждается, так что идущее в нем затухание α почти не влияет на эффективность передачи.

#магнетизм

Современный научный консенсус насчет причины возникновения стрелы времени (arrow of time) состоит в том, что все проявления направленности физических процессов – термодинамическая, квантовомеханическая, психологическая и прочая стрелы времени – обусловлены космологической стрелой времени, то есть расширением и охлаждением Вселенной.

Такую взаимосвязь проще всего понять на примере электродинамической стрелы времени: того факта, что ускоренные заряды испускают именно запаздывающие во времени электромагнитные волны, а не какие-либо иные. Представим себе электрический диполь, который некоторое время колеблется, создавая электромагнитные волны. Уравнения Максвелла для такой задачи допускают различные решения:

1) Запаздывающие волны: мы считаем, что до начала колебаний диполя электромагнитные волны в пространстве отсутствовали, а после окончания его колебаний остается расходящаяся во все стороны волна.

2) Опережающие волны: до начала колебаний диполя имеется сходящаяся к нему волна, которая, в процессе колебаний, гасится самим диполем, так что после окончания колебаний пространство не содержит волн.

3) Из-за линейности уравнений Максвелла, возможны и любые суперпозиции запаздывающего и опережающего решений, а еще к ним можно добавить любые решения уравнений Максвелла в свободном пространстве, то есть любые пролетающие мимо волны, которые могли бы существовать и без колеблющегося диполя. Таким образом, возможно бесконечно большое число решений, при которых какие-то волны имеются и до колебаний диполя, и после них.

В любом учебнике электродинамики написано, что «физичным» является лишь 1-е решение, потому что оно отвечает начальному условию отсутствия электромагнитных волн до колебаний диполя. Именно выбор 1-го решения дает начало электродинамической стреле времени: источники излучения создают расходящиеся электромагнитные волны, а не сходящиеся обратно (то есть решения 2-го вида, являющиеся обращенными во времени версиями 1-го решения) или вовсе какие-то хаотичные волны (решения 3-го типа).

Но важно понимать, что это начальное условие ставится «руками», оно не обусловлено законами физики самими по себе – потому что все перечисленные решения, в принципе, не противоречат законам физики. Так почему же мы налагаем начальное условие именно для запаздывающих волн? Потому что это соответствует практике наблюдений: пространство Вселенной можно считать почти пустым, не заполненным электромагнитными волнами. И таким оно должно быть в нашей задаче, пока диполь не начал колебаться.

Почему же пространство нашей Вселенной почти пусто? Потому что после Большого взрыва она начала быстро расширяться, имевшееся в ней вещество сконденсировалось в редко расположенные сгустки (звезды, планеты, туманности, астероиды), а имевшееся в ней излучение сильно охладилось, дав начало реликтовому излучению. А вот если бы мы решали нашу задачу о колебаниях диполя сразу после Большого взрыва, когда Вселенная кипела частицами и полями, то физически более правдоподобным было бы какое-нибудь решение 3-го типа. Наверное, можно представить себе и такую вселенную, в которой повсеместно наблюдались бы решения 2-го типа.

Таким образом, физической причиной электродинамической стрелы времени является направленность эволюции нашей Вселенной: она, будучи почти пустой и темной, с течением времени заполняется излучением (а не наоборот, опустошается, закачивая свое излучение в вещество).

#электродинамика #термодинамика #астрофизика #популярное #объяснения

Кстати говоря, примерно так же получается и с другими стрелами времени: к примеру, большинство квантовых систем в нашей Вселенной не запутаны между собой (по-видимому, опять-таки из-за ее быстрого расширения), поэтому открытая квантовая система, взаимодействующая с окружением, будет, скорее всего, запутываться с ним, теряя свою когерентность. Это дает начало квантовомеханической стреле времени.

И термодинамическая стрела времени возникает отсюда же: наша Земля непрерывно получает излучение от Солнца и отдает его в космос – это процесс, направленный электродинамической стрелой времени. Как следствие, на планете образуются концентрированные источники энергии: нагретые камни, выпадающая с дождями вода, биомасса растений, ископаемое топливо и т.д. Используя эти источники, мы разбрасываем энергию по большому числу степеней свободы, давая ей диссипировать и, в конечном итоге, улетать в космос в виде инфракрасного излучения. Психологическая стрела времени – согласно которой мы помним прошлое, но не помним будущее – также обусловлена определенной направленностью метаболических процессов в нашем организме.

В принципе, можно обращать стрелу времени вспять, создавая системы, в которых привычные нам процессы идут в обратном направлении. Такое делается, к примеру, в экспериментах с эхом Лошмидта. Но это требует изоляции системы и полного контроля над ней, потому что не так-то просто обратить общий тренд на диссипацию сконцентрированной энергии, пронизывающий весь окружающий нас мир.

#электродинамика #термодинамика #астрофизика #популярное #объяснения

Многие черты устройства и функционирования мозга демонстрируют масштабную инвариантность и фрактальность, характерные для критического режима – нахождения системы ровно в точке фазового перехода.

Авторы этой работы исследовали данные о структуре фрагментов мозга человека, мыши и мухи-дрозофиллы, представленные в виде набора плоских срезов. Как показано сверху, сопоставляя картины идущих подряд срезов, можно понять, какие сечения принадлежат одной и той же клетке и восстановить полную трехмерную структуру переплетающихся нейронов. После этого, разбивая пространство на сетки с разным шагом, можно считать критические индексы и фрактальные размерности, характеризующие такую структуру.

В качестве примера, на графике снизу показано число кубиков N_b, в которые попадают нервные клетки, как функция их размера L_b, демонстрирующее степенные зависимости с фрактальной размерностью 1.4-1.6. Вероятно, фрактальная структура мозга позволяет оптимизировать связность соединений между клетками.

#биология #самоорганизация

А вот еще интересная диаграмма из статьи об исследовании фрактальной структуры мозга. По горизонтали указана аномальная размерность η (критический индекс, описывающий спадание корреляционной функции G(r) ~ r^(–2 + d – η) с расстоянием) и фрактальная размерность d_f для различных самоподобных систем.

Исследованные образцы мозга человека, мыши и мухи-дрозофиллы показаны цветными точками, а серыми точками показаны другие исследованные системы, такие как модель трехмерной перколяции (3D Perc.), модель XY и тому подобное. Мозг по своей структуре оказывается похож на модель Изинга в гауссовом случайном поле (G. RFIM), а также перекрывается по своим свойствам с крупномасштабной структурой скоплений галактик (GC).

Получается, что сходство между структурой мозга и крупномасштабной структурой Вселенной – не иллюзия. Они действительно похожи по своим статистическим свойствам.

#биология #самоорганизация #астрофизика

Как известно, полюсы одноэлектронной функции Грина G(k,ω) дают нам информацию об энергиях квазичастиц ω = E(k). В последние годы выяснилось, что и нули функции Грина – точки в пространстве (k,ω), в которых G(k,ω) = 0 – тоже могут давать интересную информацию о свойствах многоэлектронной системы.

В этой статье выводится уйма полезных соотношений, связывающих нули функций Грина с такими величинами, как полное число электронов, холловская удельная проводимость и топологические инварианты. При выводе теоремы Латинджера, связывающей число электронов N с объемом поверхности Ферми, мы должны проинтегрировать G по импульсам и комплексным частотам, чтобы найти N ~ ∫dkdω G(k,ω)exp(iωδ). После некоторых манипуляций под интегралом оказывается выражение ∂(ln G)/∂ω – а оно дает вычеты и в полюсах, и в нулях функции Грина.

Учет нулей G, а не только ее полюсов, позволяет «починить» теорему Латинджера, которая нарушается для некоторых сильно коррелированных систем – таких, как моттовские изоляторы.

#твердое_тело

Оказывается, стрела времени-то на самом деле не простая, а зазубренная! 😱

#цитаты #квантовая_термодинамика

В этом эксперименте было обнаружено явление довольно редкого типа – квантовый фазовый переход двумерного материала 1T´-WTe₂ в состояние экситонного диэлектрика в ходе изменения уровня допирования.

Как показано на панели (b), состояние экситонного диэлектрика формируется в системе с инверсией (то есть перекрытием) энергетических зон, дисперсии которых расщепляются из-за спин-орбитального взаимодействия, а затем благодаря энергетически выгодному рождению экситонов открывается щель. Панели (e) и (f) демонстрируют главный результат: в спектре плотности состояний, полученным методом сканирующей туннельной спектроскопии, имеется щель при отрицательном затворном напряжении V.

При положительных V щель закрывается, но непосредственно вблизи уровня Ферми виден небольшой провал плотности состояний: авторы интерпретируют его как кулоновскую щель – проявление беспорядка в комбинации с кулоновским взаимодействием.

#топологические_материалы #дихалькогениды_переходных_металлов

Еще пара любопытных фактов из статьи из предыдущего поста.

Во-первых, наблюдаемое образование экситонного диэлектрика хорошо описывается довольно простой теорией: гамильтонианом с 4 энергетическими зонами, где электрон-электронное взаимодействие, приводящее к экситонному спариванию, описывается в простейшем БКШ-подобном приближении среднего поля. Сверху на рисунке можно видеть сравнение картин плотности состояний при разных уровнях допирования, измеренных в эксперименте и посчитанных теоретически.

Во-вторых, экситонный диэлектрик получается здесь не простым, а топологически нетривиальным, так что на границах образца должны существовать краевые состояния внутри щели. Снизу на рисунке показано, что на границах щель действительно закрывается: например, это видно на панели (b) из сравнения плотностей состояний, наблюдаемых в толще образца (серые кривые) и на его границе (черные кривые).

#топологические_материалы #дихалькогениды_переходных_металлов

Небольшое педагогическое введение в теорию больших отклонений (large deviation theory). Вообще, это довольно интересный аппарат, позволяющий взглянуть по-новому на многие вещи в статистике и термодинамике. Теорию больших отклонений можно рассматривать как обобщение и расширение закона больших чисел и центральной предельной теоремы.

Закон больших чисел можно сформулировать так: возьмем сумму n независимых и одинаково распределенных случайных величин X, поделенную на n: S_n = (1/n)∑ᵢXᵢ. Тогда в пределе n → ∞ усредненная случайная величина <S_n> почти наверняка будет равна среднему значению <X> той исходной величины, которая суммируется.

Иными словами, средняя арифметическая случайная величина S_n при больших n приобретает распределение, все более остро сосредоточенное вблизи своего среднего, и его дисперсия стремится к нулю. Этот принцип используется на практике при устранении случайных ошибок: чем больше сделаем измерений, тем ближе к истине будет среднее арифметическое всех результатов.

Центральная предельная теорема утверждает, что распределение величины S_n при n → ∞ будет стремиться к гауссовому распределению со средним значением <X> и дисперсией <(ΔX)²>/n. По сравнению с законом больших чисел, это более общее утверждение: мы теперь знаем не только то, что распределение S_n становится в пределе очень узким, но и насколько узким оно становится (его ширина падает как 1/√n), и какую форму оно имеет вблизи своего максимума.

Теория больших отклонений идет еще дальше: она утверждает, что распределение величины S_n имеет форму p(s) ≈ exp(–nI(s)), где I(s) – это rate function, которую на русском языке называют функцией Крамера, функцией скорости, энтропией и функцией ошибки. При s = <X> она равна нулю, а при отклонениях от этого значения положительна, поэтому и показывает, насколько быстро при n → ∞ распределение p(s) пикируется вокруг среднего.

Центральная предельная теорема получается здесь разложением I(s) в ряд Тейлора вокруг минимума при s = <X> до квадратичного порядка. Из-за квадратичной функции в экспоненте и получаем p(s) в виде распределения Гаусса. Таким образом, центральная предельная теорема показывает, как ведет себя распределение S_n при малых отклонениях вокруг среднего значения, а теория больших отклонений показывает, как оно ведет себя при любых, в том числе больших, отклонениях.

Наиболее очевидное применения такой теории – это оценка вероятностей экстремальных событий, далеко отклоняющихся от нормы. Например, землетрясение – это довольно сильное отклонение координат частиц горной породы от среднего, и потому очень маловероятное, но знание о нем – о вероятности его наступления и его характеристиках – для нас очень важно с практической точки зрения.

Далее, практически вся статистическая физика и выводимая из нее термодинамика – это, в каком-то смысле, теория больших отклонений. Там часто возникают конструкции типа exp(–nI(s)), где n – это число частиц или объем, а I(s) – интенсивная величина. Например, вероятность флуктуации в системе, связанной с окружением, ведет себя как p ~ exp(–Ns), где s – энтропия, приходящаяся на одну частицу. Преобразование Лежандра-Фенхеля, которое возникает при переходе от одного термодинамического ансамбля к другому, тоже является органичной частью теории больших отклонений.

Еще из интересного: для процесса, идущего под влиянием детерминированных факторов в сочетании со случайным шумом амплитудой ε (например, броуновского движения) вероятность реализации траектории x(t) в пределе ε → 0 ведет себя как p[x(t)] ~ exp(–I[x(t)]/ε). Это тоже форма, характерная для теории больших отклонений, с заменой n на 1/ε.

Здесь функционал I[x(t)] очень похож на действие из классической механики, так что закон больших чисел дает аналог принципа наименьшего действия: в пределе слабого шума система движется по детерминированной траектории, на которой действие зануляется. Похоже это и на фейнмановский интеграл по траекториям, где аналогом предела слабых шумовых флуктуаций ε → 0 является классический предел слабых квантовых флуктуаций ħ → 0.

#математика #стохастическая_термодинамика

Вот пара примеров, демонстрирующих возникновение асимптотики функции распределения p(s) ≈ exp(–nI(s)), описываемой теорией больших отклонений.

Функцию Крамера I(s) можно определить как предел функции –(1/n)ln p(s) при n → ∞. На графиках сверху показано, как ведут себя плотности распределения p(s) среднего арифметического n одинаковых гауссовых случайных величин и полученные из них комбинации –(1/n)ln p(s). Видно, что последние стремятся к конечному пределу – параболе I(s) = (s–1)²/2, которая и является функцией Крамера. Хотя сами функции распределения p(s) продолжают меняться при увеличении n, становясь все более острыми, их поведение можно описать универсальной асимптотикой.

На графиках снизу показано то же самое для распределения Бернулли, где с вероятностями α и 1– α выпадают 1 или 0. В пределе n → ∞ среднее арифметическое всех n выпавших величин становится непрерывной величиной, описываемой функцией Крамера I(s) = s ln(s/α) + (1 – s)ln[(1 – s)/(1 – α)].

#математика #стохастическая_термодинамика

Универсальная фраза, которую можно добавить в любую статью.

#цитаты

А вот статья с довольно математизированным описанием применений теории больших отклонений в статистической физике. Основной посыл статьи в том, что возможны три уровня описания статистических систем, перекочевывающие и в теорию больших отклонений.

1-й уровень описания – это расчет средних по статистическому ансамблю значений наблюдаемых величин. Теория больших отклонений на этом уровне дает информацию о том, как именно и с какой скоростью флуктуирующие значения наблюдаемых сосредотачиваются вокруг своих средних при росте числа частиц, объема или с ростом времени – по мере того, как система стремится к термодинамическому равновесию.

2-й уровень описания – рассмотрение всего статистического распределения случайной величины. Теория больших отклонений показывает здесь, как распределение стремится к своей предельной форме – например, к распределению Гиббса для энергии или к гауссовому распределению для флуктуаций параметра порядка. Здесь возникают такие величины, как расхождение Кульбака-Лейблера, энтропия Шеннона и другие величины, сближающие статистическую физику с теорией информации.

Наконец, 3-й уровень описания – это распределение траекторий системы, то есть не просто статистического ансамбля, а его эволюции с течением времени. Здесь теория больших отклонений позволяет исследовать общие закономерности поведения системы с течением времени. Например, хаотическую динамику, обусловленную ростом энтропии Колмогорова-Синая.

#стохастическая_термодинамика #термодинамика