А вот более современный и обстоятельный обзор о связанных состояниях в континууме для электромагнитных волн в диэлектрических, металлических и гибридных структурах. В отличие от предыдущего обзора, он направлен уже не на объяснения принципов, а на перечисление того, что сделано в этой области исследований в последние годы. И она действительно невероятно быстро развивается.

Авторы описывают основные реализации электромагнитных связанных состояний в континууме: фотонные кристаллы в виде двумерных периодических структур (это либо тонкий слой металла или диэлектрика, либо что-то, изготовленное или даже нацарапанное на поверхности трехмерного материала), трехмерные слоистые структуры и одномерные нити.

Подробно описываются и возможные их применения: лазерная генерация, направление излучения в нужную сторону, сенсоры, создание киральных лучей и структурированного света, переключатели, локальное усиление поля и нелинейная генерация гармоник.

#фотоника #электродинамика

Раз уж сегодня у нас день связанных состояний в континууме, покажу еще один интересный факт.

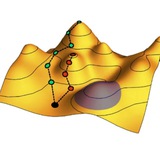
На рисунке показан двумерный фотонный кристалл, в котором образуются связанные состояния в континууме, показанные пиками добротности на диаграмме сверху: одно симметрийно-защищенное при k = 0 и еще 4 состояния Фридриха-Уинтгена при k ≠ 0.

Оказывается, все они являются топологическими дефектами для поля линейной поляризации света, прошедшего через кристалл и детектируемого в дальнем поле. Симметрийно-защищенное состояние является вихрем заряда –1, состояния Фридриха-Уинтгена – вихрями заряда +1. Эти вихри образуются на пересечении зеленых и красных линий, где зануляются, соответственно E_x и E_y – поэтому в таких точках весь вектор E в дальнем поле обращается в ноль.

Из-за топологической нетривиальности, вихри оказываются весьма устойчивыми к малым изменениям параметров системы. Но сильным изменением параметров два вихря зарядов +1 и –1 можно заставить аннигилировать, как показано снизу.

#фотоника #электродинамика

Неопределенность результатов квантового измерения может использоваться для генерации истинно случайных чисел – и действительно, уже давно существуют пусть и не самые быстрые, но хорошие квантовые генераторы случайных чисел. В этой же работе рассматривается более амбициозная задача: можно ли при помощи квантовых эффектов организовать не зависящую от устройства сертифицированную генерацию истинно случайных чисел?

Под такой генерацией имеется в виду следующее:
1) Генерируемые числа полностью случайны, они никак не скоррелированы между собой ни в каких комбинациях.
2) Генерируемые числа устойчивы к враждебным атакам – это означает, что никакой внешний наблюдатель, подчиняющийся законам физики, не сможет их предугадать, независимо от своей вычислительной мощности.
3) Алгоритм генерации должен быть универсальным: надежность его работы не должна зависеть от архитектуры устройства, на котором он запускается.

Второй пункт особенно важен, если мы используем случайные числа для шифрования или для выбора стратегии в соревновательных играх. Пример чисел, полностью случайных (удовлетворяющих 1-му требованию), но уязвимых с точки зрения информационной безопасности, иллюстрируется «атакой при помощи флешки». Представим себе, что провайдер случайных чисел генерирует последовательность таких чисел, записывает их на флешку и продает потребителю. С точки зрения потребителя, это хорошие случайные числа, которые успешно пройдут все статистические тесты. Но проблема в том, что все они известны провайдеру, который, пользуясь этим знанием, может предпринять против потребителя враждебную атаку.

Предлагаемый авторами алгоритм, удовлетворяющий всем трем условиям, основывается на квантовой запутанности и моногамии квантовых корреляций. Для его работы нужны две квантовые системы 1 и 2, которые на каждом шаге генерации приводятся в состояние квантовой запутанности. Затем, на основе параметров измерений x₁ и x₂, которые можно менять по желанию, каждая система выдает результаты измерения a₁ и a₂. Для того, чтобы убедиться в сертифицированной случайности чисел, получаемых в результате постпроцессинга последовательности пар a₁ и a₂, нужно, чтобы условная вероятность P(a₁a₂|x₁x₂) нарушала неравенство Белла – а именно, некоторая сумма всех P(a₁a₂|x₁x₂) с коэффициентами, зависящими от аргументов, должна превышать максимальный предел, достижимый классически скоррелированным состоянием систем 1 и 2.

Если неравенство Белла нарушается – то есть системы 1 и 2 находятся в квантово запутанном состоянии – значит, наш генератор случайных чисел действительно сертифицирован. Причиной этому служит моногамия квантовых корреляций: если системы 1 и 2 максимально квантово запутаны между собой, то они не могут быть квантово запутаны с чем-либо еще – в том числе, и с предполагаемым злоумышленником. Следовательно, никто не может знать заранее, какими эти числа получатся.

На самом деле это, конечно, вопрос количественный: системы 1 и 2 могут быть запутаны между собой лишь частично, а частично – со злоумышленником, так что неравенство Белла будет нарушаться, но достаточно слабо. Тем не менее, даже такая ситуация поддается контролю. Авторы показывают, что если мы к примеру, считаем на основе статистики P(a₁a₂|x₁x₂) параметр Клаузера-Хорна-Шимони-Хольта, то превышение им значения 2 свидетельствует, как минимум, о существовании неклассических корреляций между двумя системами. Если этот параметр превышает 2√2, то классический злоумышленник не сможет предсказать наши случайные числа – для этого он должен быть существенно квантовым. Если же этот параметр достигает 4, то наши числа будут недоступны для предсказания любому злоумышленнику, неспособному передавать сигналы быстрее скорости света.

#квантовая_механика #квантовые_вычисления

Мини-обзор по сканирующей туннельной микроскопии и спектроскопии электронных состояний внутри вихрей в d-волновых высокотемпературных сверхпроводниках.

Теория предсказывает, что связанные электронные состояния внутри вихря в d-волновом сверхпроводнике должны давать пик локальной плотности состояний на уровне Ферми – так называемый zero-bias conductance peak, пример которого показан на панели (c). В то же время, в обычном, s-волновом сверхпроводнике внутри вихря должны наблюдаться два расщепленных пика Кароли-де Жена-Матрикона, как показано на панели (d).

Удивительно, что эксперименты часто показывают практически противоположную картину: расщепленные пики в d-волновых сверхпроводниках (a) и единственный пик в s-волновых (b). Это противоречие долгое время смущало исследователей, и только в последние годы стали выясняться его причины: недостаточное экспериментальное разрешение (из-за чего два пика сливались в один), влияние примесей, псевдощели, волн зарядовой плотности и тому подобное.

#сверхпроводимость

Эффект Физо заключается в увлечении света движущимся диэлектриком. А в этом эксперименте был реализован аналог эффекта Физо – увлечение света светом с использованием атомного газа в качестве посредника.

Если я все правильно понял, суть эксперимента в следующем: лазерный луч накачки создает в атомном газе узкое окно электромагнитно-индуцированной прозрачности. Но частота этого окна отстроена от частоты зондирующего луча на величину Δ, для компенсации которой нужно двигаться в лабораторной системе отсчета. Можно сказать, что луч накачки «подсвечивает» в атомном газе группе атомов, движущихся из-за его отстройки со скоростью v ~ Δ, в которых открывается окно прозрачности для зондирующего луча.

Так и получается аналог эффекта Физо: движущаяся подгруппа атомов увлекает за собой зондирующий луч, так что в детектор он поступает с дополнительным разгоном, отвечающим скорости v_gr. Согласно теории, эта скорость должна вести себя как v_gr ~ Δ², и результаты измерений это подтверждают.

#атомные_газы #фотоника

Эксперименты по проверке неравенств Белла, удостоенные в прошлом году Нобелевской премии по физике, опровергли локальный реализм: это представление о том, что в квантовых системах все измеряемые величины в каждый момент времени имеют определенные значения – независимо от того, измерены они, или еще нет.

В более общем случае, эксперименты по проверке неравенств Белла опровергли локальные теории скрытых параметров. Согласно таким теориям, результаты измерений, проведенных над квантовой системой, зависят – детерминистически или стохастически – от некоторого набора не поддающихся непосредственному определению скрытых параметров λ. Локальность же – это концепция, согласно которой системы, переставшие между собой взаимодействовать и разошедшиеся на большое расстояние, не могут повлиять друг на друга.

Представим, что мы, как обычно делается в экспериментах по проверке неравенств Белла, создаем две запутанные между собой квантовые системы и разводим их на большое расстояние Δr – так, чтобы разделяющий их интервал был пространственноподобным, Δr > cΔt. Проводя над каждой системой измерения согласно управляемым параметрам a и b (это, например, ориентации детекторов, определяющих проекцию спина каждой из двух запутанных между собой частиц), мы получаем результаты измерений A и B (например, проекции фотонных спинов ±1). Согласно локальным теориям скрытых параметров, совместная вероятность получения этих результатов измерений должна иметь вид P(A,B|a,b,λ) = P(A|a,λ)P(B|b,λ). Локальность здесь проявляется в факторизации распределения на два сомножителя, а теория скрытых параметров – в их зависимости от общего набора параметров λ, случайность которых и обеспечивает случайный характер результатов A и B. В отличие от упомянутого выше локального реализма, где зависимости P(A|a,λ) и P(B|b,λ) детерминистичны (то есть комбинация a и λ однозначно определяет A, а комбинация b и λ однозначно определяет B), в теориях скрытых параметров они могут быть, вообще говоря, стохастическими.

Нарушения неравенств Белла, подтвержденные в экспериментах, продемонстрировали, что совместное распределение вероятностей P(A,B|a,b,λ) не может иметь факторизованную форму P(A|a,λ)P(B|b,λ). А это значит, что либо зависимость от скрытого параметра λ существенно нелокальна – это исключает представления о том, что «каждая из двух систем еще до измерения имела определенное состояние», – либо никаких скрытых параметров не существует, так что одной лишь волновой функции совокупности двух систем достаточно для полного определения всей статистики совместных измерений P(A,B|a,b).

Но во всех этих рассуждениях есть лазейка, называемая freedom-of-choice loophole. А именно: а кто сказал, что при каждом запуске эксперимента мы действительно случайно и действительно свободно выбираем параметры измерений a и b? На математическом уровне это сводится к вопросу о совместном распределении параметров P(a,b,λ), которые, умножаясь на P(A,B|a,b,λ), должны давать реально наблюдаемую статистику измерений P(A,B) = P(A,B|a,b,λ)P(a,b,λ). В экспериментах параметры a и b менялись как детерминистически, так и случайно, но все равно нужно доказать, что этот выбор никак не зависел от скрытых параметров λ, фиксирующихся в момент создания запутанной пары систем.

Иными словами, наблюдавшиеся нарушения неравенств Белла исключают локальные теории скрытых параметров только в том случае, если P(a,b,λ) = P(a)P(b)P(λ), что отнюдь не очевидно. Если же распределение P(a,b,λ) скоррелировано, то теория скрытых параметров может работать даже при формальном нарушении неравенства Белла. В этой работе 2010 года такая лазейка свободы выбора была закрыта: было продемонстрировано, что неравенства Белла нарушаются даже при постановке эксперимента, исключающей коммуникацию (со скоростью, не превышающей скорость света) между точкой создания запутанных систем (где определяется λ) и точками генерации случайных параметров измерений a и b.

#квантовая_механика #объяснения #отвал_башки

Кстати говоря, в рассуждениях о теориях скрытых параметров, локальном реализме и свободе выбора из предыдущего поста есть еще один нюанс.

Эксперимент по проверке неравенств Белла, закрывающий лазейку свободы выбора, исключает возможность того, что скрытые параметры λ, если они существуют, могут как-то повлиять (со скоростью коммуникации, не превышающей скорость света) на выбор параметров измерений a и b над запутанными системами.

Но он никак не исключает еще одну возможность: а что, если все параметры λ, a и b на самом деле связаны между собой не причинно-следственными связями, а общей зависимостью от какого-то третьего параметра μ? Например, значения λ, a и b, выпадающие при каждом запуске эксперимента, определило какое-то событие, произошедшее еще в далеком прошлом.

Частным случаем такого сценария является сверхдетерминизм: можно представить, что вся история Вселенной заранее предопределена. И все результаты экспериментов над квантовыми системами заранее предопределены таким образом, чтобы нам они казались случайными и не противоречащими законам квантовой механики. Но и стохастические варианты зависимости параметров λ, a и b от μ, в принципе, возможны: в этом случае история Вселенной не предопределена полностью, но случайные величины, выдаваемые квантовыми генераторами случайных чисел, разделенными пространственноподобными интервалами, тоже могут быть скоррелированы между собой неким непостижимым для нас образом.

Авторы признают, что мы пока не можем придумать постановку эксперимента, исключающую такие сценарии сверхдетерминизма и сверхреализма. Поэтому такие варианты теорий – в том числе, полная предопределенность всех событий во Вселенной – нефальсифицируемы и не могут быть опровергнуты эмпирическими методами.

#квантовая_механика #объяснения #отвал_башки

Вот некоторые детали насчет того, как в эксперименте по проверке неравенств Белла была закрыта лазейка свободы выбора.

Эксперимент проводился на двух Канарских островах – Пальма и Тенерифе. В лаборатории на острове Пальма генерировалась пара запутанных фотонов. Если справедливы локальные теории скрытых параметров, то их значения λ уже в этой точке должны определиться. На этом же острове, на расстоянии 1.2 км, при помощи квантового генератора случайных чисел определялось значение параметра a – направления детектирования спина первого фотона (45° или 0°). Второй фотон летел на остров Тенерифе на расстояние 144 км, где второй квантовый генератор случайных чисел заранее определял параметр b – направления измерения поляризации второго фотона (22.5° или 67.5°).

Все расстояния и тайминги были подобраны таким образом, чтобы точки, в которых определяются λ, a и b, были разделены пространственноподобными интервалами, исключающими любую причинно-следственную связь между их выборами.

#квантовая_механика #отвал_башки

Черный фосфор – это слоистый материал, монослой которого имеет анизотропную кристалличкскую структуру. Она выглядит как решетка «пчелиные соты», но периодически изгибающаяся в одном направлении и ровная в другом.

Электронные и оптические свойства однослойного черного фосфора тоже анизотропны, и в этой работе в нем наблюдались существенно анизотропные экситоны. Рисунок слева показывает расчетную волновую функцию экситона (точнее, распределение электрона при зафиксированном положении дырки в белой точке), вытянутую в x-направлении. И действительно, на диаграммах справа можно видеть, что интенсивность люминесценции на частоте экситонов гораздо выше при накачке и детектировании в x-направлениях, чем в других, из-за анизотропии дипольного момента перехода.

Интересно также, что экситоны имеют огромную энергию связи 0.9 эВ. И хотя щель в черном фосфоре 2.2 эВ лежит в видимом диапазоне (560 нм), из-за большой энергии связи энергия экситонов 1.3 эВ опускается до ближнего инфракрасного диапазона (950 нм).

#экситоны

Очередное исследование, посвященное вопросу «почему нейронные сети обучаются гораздо эффективнее, чем ожидается исходя из теории»? Здесь на нескольких примерах, поддающихся аналитическому изучению, показывается, что нейронные сети при своем обучении довольно быстро достигают широких плоских минимумов ландшафта функции ошибок.

На заре развития науки о нейронных сетях считалось, что они при своем обучении будут часто застревать в локальных минимумах функции ошибок, что будет мешать их эффективной работе. Но тогда нейросети были маленькие из-за малой мощности компьютеров, а современные нейросети, наоборот, сверхпараметризованы – это значит, что число их параметров (весов межнейронных связей и смещений) значительно выше числа условий, которым нужно удовлетворить, чтобы полностью свести ошибку к нулю на обучающей выборке. Поэтому нет особой проблемы в том, чтобы достичь глобального – равного нулю – минимума функции ошибок. Проблема только в том, что этих минимумов очень много и не все они одинаково хороши с точки зрения качества.

Авторы этой работы показывают, что подавляющее большинство минимумов функции ошибок располагаются в пространстве параметров довольно рассеянно и изолированно друг от друга. Но есть небольшая доля минимумов, скапливающихся в локальные сгустки – можно предположить, что нейросеть, попавшая при обучении в такие сгустки, будет работать более эффективно из-за лучшей способности к обобщению. А именно, вместо прямолинейного заучивания обучающей выборки нейросеть улавливает в предъявляемых ей данных что-то осмысленное, о чем свидетельствует свобода выбора одного из большого числа находящихся рядом минимумов. Если же нейросеть попала в изолированный минимум, то она, скорее всего, переобучилась: малейший отход от установившихся параметров в любом направлении резко повышает ошибку, что свидетельствует о негибкости результата обучения.

И вот что интересно: если искать минимум функции ошибок, к примеру, методом симулированного отжига или каким-нибудь простым жадным алгоритмом, то нейросеть, скорее всего, попадет в один из изолированных локальных минимумов – просто потом, что их подавляющее большинство. В то же время, традиционные алгоритмы минимизации ошибок, по-видимому, приводят нейросеть, наоборот, в широкие плоские локальные минимумы – то есть в локальные сгустки минимумов в пространстве параметров.

Авторы показывают это на примере минимизации функции ошибок в виде кросс-энтропии в задаче дискретной классификации – оказывается, что минимум кросс-энтропии ведет процесс оптимизации не просто к нулю ошибок классификации на всей обучающей выборке (как говорилось выше, у сверхпараметризованной сети таких нулей очень много), а к нулю ошибок в комбинации с высокой плотностью минимумов. Могу предположить, что примерно такую же роль играет регуляризация весов, не дающая сети переобучаться.

Таким образом, на ландшафте функции ошибок нейросети встречаются широкие плоские минимумы, которые можно трактовать как скопления большого числа либо низко расположенные почти плоские плато. Эффективность обучения нейросетей, по-видимому, связаны с попаданием именно на такие плато, а не в изолированные локальные минимумы. Хотя, с другой стороны, авторы рассмотрели лишь ограниченный набор относительно простых архитектур сетей и алгоритмов из-за исключительной математической сложности анализа процесса обучения, так что нужно ждать появления более общих выводов.

#нейронные_сети

Процесс перемагничивания ферромагнетика с одного направления намагниченности на обратное происходит в виде последовательности лавин – резкого перемагничивания отдельных доменов, наблюдаемого как эффект Баркгаузена.

В этом эксперименте при помощи магнитооптического эффекта Фарадея наблюдали, как перемагничивается тонкая ферромагнитная пленка. Этот процесс идет из центра во все стороны в виде расширяющегося почти круглого фронта. Но при достаточном разрешении видно, что фронт изрезанный и движется рывками – это называют процессом депининга, протаскивания натянутой упругой нити через неупорядоченный потенциальный ландшафт.

При каждом рывке происходит перемагничивание домена, идентификация которых показана на рисунке снизу. Анализ показывает, что площади и продольные длины этих доменов описываются масштабно-инвариантной степенной статистикой, характерной для лавин в самоорганизующихся системах.

#магнетизм #самоорганизация

Вот это очень красивый и остроумный эксперимент с демонстрацией метода времяразрешенной емкостной спектроскопии, позволяющей получать картину плотности состояний двумерной системы.

Как показано на панелях (a)-(b), у нас имеется полупроводниковая квантовая яма (изучаемый объект), помещенная между двумя электродами, причем левый электрод отделен от нее лишь тонким туннельным барьером. Импульс напряжения, прикладываемый между электродами (c), запускает в квантовую яму электроны слева, а скорость их поступления – туннельный ток – определяется по скорости накопления на них заряда в самом начале этого процесса (d). Меняя амплитуды V импульса напряжения, можно сканировать (e) туннельный ток I как функцию V, получая картину плотности состояний ρ(E_F + eV) ~ dI/dV, как и в обычной туннельной спектроскопии (f).

На диаграммах снизу показаны картины плотности состояний в магнитном поле как функции уровня допирования, на которых видны уровни Ландау и их спиновые расщепления.

#твердое_тело #уровни_Ландау

Закон Ципфа часто встречается в статистике сложных самоорганизующихся систем, имеющей дело объектами сильно различающихся размеров. Согласно этому закону, если мы отсортируем объекты по убыванию их размеров s, мы получим кривую s ~ 1/kᵞ, где k – ранг объекта (k = 1 у самого большого, k = 2 у второго по величине и т.д.). Этот закон много раз открывался и переоткрывался разными исследователями – и неудивительно, ведь он выполняется для
• населенностей городов,
• ВВП стран,
• бюджетов фирм,
• частот встречаемости слов в тексте, деталей конструкторов LEGO в игровом наборе и белков каждого вида в живой клетке,
• размеров скоплений галактик,
• мощностей солнечных вспышек, землетрясений и цунами,
• размеров осколков при разбивании хрупкого предмета,
• посещаемости сайтов,
• числа погибших в войнах и террористических атаках,
и много другого.

С законом Ципфа тесно связан закон Лотки для распределения вероятности p(s) ~ 1/sᵝ встретить объект размером s, где β = (γ+1)/γ. Его легко вывести: возьмем небольшой интервал на оси рангов k, отвечающий Δk = 1 – одному-единственному объекту, тогда из закона Ципфа s ~ 1/kᵞ мы получаем интервал на оси размеров s, равный Δs ~ 1/kᵞ⁺¹. С другой стороны, вероятность встретить этот объект в интервале размеров от s до s+Δs равна, по определению плотности вероятности, p(s)Δs, и она же равна 1. Отсюда находим p(s) ~ 1/Δs ~ kᵞ⁺¹ ~ 1/s⁽ᵞ⁺¹⁾ᐟᵞ.

Законы Ципфа и Лотки свидетельствуют о масштабной инвариантности системы, то есть об отсутствии характерного размера. К примеру, энергия s, выделившаяся в землетрясениях, подчиняется закону p(s) ~ s⁻³ᐟ² для s, простирающихся на несколько порядков величин. Это означает, что нет какого-то «характерного» размера землетрясения s, определяющего общий порядок этой величины – в отличие от, например, человеческого роста, распределенного по закону Гаусса и имеющего среднюю величину 170 см.

Конечно же, степенное распределение p(s) ~ 1/sᵝ не может простираться на шкале s от нуля до бесконечности – хотя бы потому, что оно не нормируемо на единицу. И закон Ципфа, и закон Лотки справедливы в очень широком, простирающемся на несколько порядков, но все-таки ограниченном диапазоне величин s. Для учета обрезания распределения на очень высоких s иногда вместо закона Ципфа используют модифицированный закон Ципфа-Мандельброта s ~ 1/(k + Q)ᵞ, где параметр Q > 0 не дает размерам s слишком сильно расти при малых k.

Исследователями делались разные попытки как-то объяснить или вывести закон Ципфа, но общепринятого объяснения пока что не существует. Одна из таких попыток была сделана Мандельбротом: он пытался объяснить закон Ципфа для частоты встречаемости слов в естественных языках из соображений максимальной эффективности кодирования информации. Если мы представим, что наиболее часто встречающиеся слова должны быть самыми короткими (такие, как “the” в английском языке), то соображения максимизации суммарной информации Шеннона, переносимой достаточно большим набором слов, в сочетании с минимизацией общей длины текста, дают как раз закон Ципфа для частоты встречаемости слов.

Простая модель, где возникает закон Ципфа – это мультипликативный процесс, при котором размер каждого объекта на каждом шаге времени меняется как s(t+1) = r(t)s(t), где r(t) – случайно флуктуирующая величина. Это можно считать простой моделью рынка, где стоимость каждого актива растет или падает пропорционально его текущей стоимости. После достаточно большого числа шагов исходно случайное распределение размеров s превращается в степенное, описываемое законом Лотки.

Еще одна модель, где такое возникает – это модель Юла-Саймона, или модель предпочтительного присоединения. Представим, что человек, прибывающий в страну, с какой-то вероятностью h поселяется в одном из уже существующих городов, причем вероятность выбора каждого города пропорциональна его текущему населению s. А с вероятностью 1 – h он основывает новый город с населением 1. Тогда, после большого времени, распределение городов по населенностям s будет описываться законом Лотки p(s) ~ s⁽²⁻ʰ⁾ᐟ⁽¹⁻ʰ⁾.

#самоорганизация #общество #популярное #объяснения

Вот пара примеров законов Ципфа и Лотки, описывающих степенную статистику сложных систем.

Сверху на рисунке – частоты встречаемости s слов каждого вида в романе Германа Мелвилла «Моби Дик». Они подчиняются закону Ципфа s ~ 1/k, который на логарифмических шкалах по обеим осям выглядит как прямая линия ln s = – ln k + C. Второе по встречаемости слово of появляется примерно в 2 раза реже, чем самое частое слово the, следующее слово a – примерно в 3 раза реже и т.д..

Снизу показан пример выполнения закона Лотки для продуктивности 5401 художников из всей Европы, написавших суммарно 14155 картин на протяжении 500 лет от Средних веков до современности. Больше всего художников, написавших всего по одной картине; художников, написавших по 2 картины, в 4 раза меньше, по 3 – в 9 раз меньше и т.д. Таким образом, вероятность встретить художника, написавшего s картин, подчиняется закону обратных квадратов p(s) ~ 1/s².

#самоорганизация #общество #популярное #объяснения

Кинетическое уравнение Больцмана для частиц в сферически-симметричном гармоническом потенциале предсказывает существование монопольной «дышащей» моды: периодического расширения и сжатия системы частиц, происходящего полностью изотропно. Интересно, что такая мода не затухает, несмотря на наличие столкновений между частицами, которые, казалось бы, должны вести систему к состоянию теплового распределения.

В этом эксперименте монопольная мода наблюдалась в газе атомов рубидия, помещенных в очень ровную гармоническую ловушку. На графиках показаны измеренные колебания монопольной и, для сравнения, квадрупольной моды. Видно, что монопольная мода действительно практически на затухает: время ее жизни около 30 секунд, в то время как квадрупольная мода затухает примерно за 1 секунду.

Остаточное затухание обусловлено, как считают авторы, слабой анизотропией ловушки в районе 0.05%, из-за которой монопольная мода связывается с короткоживущей квадрупольной и отдает ей свою энергию.

#атомные_газы #термодинамика

Действительно, давайте найдем эффективную эффективность тепловой машины.

#стохастическая_термодинамика #цитаты

Гильбертово пространство состояний квантовой системы очень обширно. Те состояния системы, которые в принципе могут нам встретиться в любой реалистичной физической задаче, занимают лишь небольшой его уголок, который называют physical corner.

Вот работа, в которой это иллюстрируется. Авторы показывают, что если мы возьмем квантовую систему в некотором «референсном» состоянии (это может быть основное состояние, вакуум или ферромагнетик) и начнем подвергать ее эволюции под действием локального гамильтониана в течение времени, полиномиального по размеру системы, то множество состояний, которые система сможет таким образом достичь, будет занимать лишь экспоненциально малую долю всего гильбертова пространства. Здесь предполагается, что гамильтониан является k-локальным (то есть состоит из слагаемых, каждое из которых действует на степени свободы не более чем k частиц), а спектр его энергий ограничен.

С малостью объема физического угла связан успех теоретических методов, описывающих волновые функции квантовых многочастичных систем при помощи относительно простых анзацев – определителей Слэтера, вариационных функций БКШ, матричных и тензорных произведений и т.д.

Стоит отметить, что «классические» состояния любой квантовой системы, которые отвечают ее состояниям, наблюдаемым нами в повседневной жизни, занимают еще меньшую долю гильбертова пространства – так называемый классический домен. Он окружен небольшим квантовым гало – теми неклассическими состояниями, до которых мы можем дотянуться своими экспериментами.

#квантовая_механика

А вот интересная формула из статьи из предыдущего поста. Она ограничивает сверху различие между результатом хронологически упорядоченной эволюции в течение небольшого промежутка времени Δt и такой же эволюции, но без хронологического упорядочения T.

Различие между ними ограничивается максимальной нормой гамильтониана за весь промежуток времени и самим этим промежутком времени. Напомню, что норма ||A|| оператора A – это максимальный модуль его матричных элементов |<φ|A|ψ>| по всем нормированным на единицу векторам |φ> и |ψ > гильбертова пространства.

Физический смысл этой формулы в том, что можно пренебречь флуктуацями гамильтониана на малых промежутках времен, из за которых гамильтониан в разные моменты времени не коммутирует сам с собой, так что его операторную экспоненту приходится хронологически упорядочивать.

#квантовая_механика

Стрелой времени называют преимущественную направленность множества наблюдаемых физических процессов во времени: тепло переходит от горячих тел к холодным, а не наоборот, открытая квантовая система теряет свою когерентность, запутываясь с окружением, наш мозг помнит события прошлого, но не «помнит» будущее и т.д.

В этой работе демонстрируется и экспериментально проверяется соотношение между средним производством энтропии <Σ>, происходящей в квантовой системе за время от 0 до τ, с асимметрией ее динамики во времени – той самой стрелой времени. Это соотношение выглядит как <Σ> = S(ρ^F(t) | ρ^B(τ–t)), где S – расхождение Кульбака-Лейблера между двумя матрицами плотности, ρ^F(t) – матрица плотности системы, начинающей свою эволюцию с равновесного состояния в момент времени 0 до любого промежуточного момента времени t, а ρ^B(τ–t) – матрица плотности системы, эволюционирующей обратно во времени с момента τ до текущего момента t.

Таким образом, производство энтропии <Σ> – термодинамическая мера необратимости процесса, пропорциональная энергии T<Σ>, переходящей в тепло, – связывается с информационной мерой необратимости этого процесса – а именно, с мерой того, насколько сильно нарушается симметрия эволюции системы во времени. В отсутствие стрелы времени прямая эволюция системы от 0 до t давала бы ровно такой же результат, как и обратная эволюция от τ до t, тогда расхождение Кульбака-Лейблера между двумя матрицами плотности было бы равно нулю, и диссипация энергии тоже отсутствовала бы.

#термодинамика #квантовая_термодинамика

А вот результаты эксперимента по проверке связи между стрелой времени – необратимостью эволюции квантовой системы – и производством энтропии.

Квантовой системой служил кубит, построенный на двух ориентациях ядерного спина ¹³C в молекуле хлороформа. Эволюция кубита вперед (от 0 до τ) назад (от τ до 0) во времени начиналась с равновесных состояниях и шла под действием противоположных во времени изменений его гамильтониана, реализуемых его облучением микроволнами.

Диаграмма снизу показывает, как при этом меняется вектор состояния кубита на блоховской сфере: по мере того, как в ходе прямой и обратной эволюции вектор гамильтониана движется вдоль одной и той же зеленой линии, но в обратных направлениях, векторы состояния отходят от этой линии из-за неравновесности динамики, причем по-разному при разных ее направлениях. На графике показано подтверждение связи между производством энтропии <Σ> и асимметрией матриц плотности, справедливой по все моменты времени t от 0 до τ.

#термодинамика #квантовая_термодинамика

В этой теоретической работе было предсказано существование экситонов с линейной дисперсией в двумерных дихалькогенидах переходных металлов: зависимость их энергии от импульса центра масс электрона и дырки напоминает световой конус. Как показано на графике сверху, в MoS₂ существуют не только безмассовые внутридолинные экситоны, но и две ветви массивных экситонов, расщепленные по спину.

Возникновение линейного по импульсу Q вклада в энергию экситона объясняется обменным взаимодействием: процессом виртуальной аннигиляции электрона и дырки, добавляющей к энергии слагаемое ΔE ~ |<ex(Q)|p|0>|²v(Q), где v(Q) = 2πe²/Q – двумерное кулоновское взаимодействие, <ex(Q)|p|0> ~ Q – матричный элемент аннигиляции экситона (его превращения в вакуум), которая запрещена правилами отбора ровно в дираковской точке Q = 0, но становится разрешенной при Q ≠ 0. В итоге получается неаналитическая зависимость ΔE ~ |Q| энергии от импульса.

#экситоны #дихалькогениды_переходных_металлов