А вот наглядный пример из статьи с сопоставлением классической и квантовой адиабатической эволюции. Авторы рассмотрели двухуровневую квантовую систему и ее классический аналог, который, из-за наличия отрицательно-частотных уровней, обладает 4 состояниями.
На графиках показаны четыре примера модуляции энергии двух уровней с течением времени (красная и синяя кривые) и соответствующего поведения амплитуд заселения энергетических уровней для квантовой (черная и красная кривые) и классической (остальные цвета) систем.
В случае 1 все адиабатично: и щель между уровнями, и сами их энергии велики, так что обе системы остаются в прежних состояниях. Если щель остается большой, но сама энергия нижнего уровня почти достигает нуля (случай 2), то квантовая система ведет себя адиабатично, а классическая – уже нет. В случаях 3 и 4 щель между уровнями временами сильно уменьшается, так что обе системы переходят на с начального уровня на другие – хотя и по-разному в случае 3.
#квантовая_механика #механика #отвал_башки
На графиках показаны четыре примера модуляции энергии двух уровней с течением времени (красная и синяя кривые) и соответствующего поведения амплитуд заселения энергетических уровней для квантовой (черная и красная кривые) и классической (остальные цвета) систем.
В случае 1 все адиабатично: и щель между уровнями, и сами их энергии велики, так что обе системы остаются в прежних состояниях. Если щель остается большой, но сама энергия нижнего уровня почти достигает нуля (случай 2), то квантовая система ведет себя адиабатично, а классическая – уже нет. В случаях 3 и 4 щель между уровнями временами сильно уменьшается, так что обе системы переходят на с начального уровня на другие – хотя и по-разному в случае 3.
#квантовая_механика #механика #отвал_башки
Встречайте HeLIOS (Helium ultraLIght dark matter Optomechanical Sensor) – детектор для гипотетических сверхлегких частиц темной материи, основанный на сверхтекучем гелии-4. Он представлен герметичным цилиндрическим сосудом с жидким гелием, сверху накрытым тонкой металлической мембраной с выступом в центре. Мембрана служит нижней стенкой небольшого микроволнового резонатора с резонансной частотой, чрезвычайно чувствительной к ее малым вертикальным сдвигам.
Если темная материя состоит из сверхлегких частиц массой меньше 10 эВ, их плотность должна быть достаточно велика для формирования классической волны – подобно классической электромагнитной волне, получающейся при большой плотности фотонов. Волна скалярных частиц может, предположительно, создавать в массе гелия осциллирующие натяжения, возбуждающие «дышащие» моды (с четными индексами на рисунке), а волна векторных частиц – осциллирующую силу, возбуждающую моды с нечетными индексами.
#астрофизика #сверхтекучесть
Если темная материя состоит из сверхлегких частиц массой меньше 10 эВ, их плотность должна быть достаточно велика для формирования классической волны – подобно классической электромагнитной волне, получающейся при большой плотности фотонов. Волна скалярных частиц может, предположительно, создавать в массе гелия осциллирующие натяжения, возбуждающие «дышащие» моды (с четными индексами на рисунке), а волна векторных частиц – осциллирующую силу, возбуждающую моды с нечетными индексами.
#астрофизика #сверхтекучесть
А вот диаграммы из статьи из предыдущего поста, показывающие возможности нового детектора HeLIOS для частиц темной материи в сравнении с другими существующими детекторами.
Красным цветом показаны диапазоны масс частиц (по горизонтали) и силы их взаимодействия с материей (по вертикали), покрываемые HeLIOS. Две диаграммы отвечают скалярным и векторным частицам, по-разному взаимодействующими с материей: скалярные частицы могут модулировать постоянную тонкой структуры или массу фермионов, а векторные могут раскачивать материю осциллирующей силой.
Благодаря тому, что детектор использует целый набор стоячих мод звуковых колебаний сверхтекучего гелия в сосуде, а их частоты могут перестраиваться изменением давления, удается покрыть довольно широкий диапазон масс.
#астрофизика #сверхтекучесть
Красным цветом показаны диапазоны масс частиц (по горизонтали) и силы их взаимодействия с материей (по вертикали), покрываемые HeLIOS. Две диаграммы отвечают скалярным и векторным частицам, по-разному взаимодействующими с материей: скалярные частицы могут модулировать постоянную тонкой структуры или массу фермионов, а векторные могут раскачивать материю осциллирующей силой.
Благодаря тому, что детектор использует целый набор стоячих мод звуковых колебаний сверхтекучего гелия в сосуде, а их частоты могут перестраиваться изменением давления, удается покрыть довольно широкий диапазон масс.
#астрофизика #сверхтекучесть
Когерентные машины Изинга (или квантово-оптические нейронные сети) способны быстро находить решения экспоненциально трудных оптимизационных задач благодаря комбинации квантовых и нелинейных эффектов. Авторы этой работы откладывают в сторону квантовые эффекты и анализируют, что происходит при этом с самим энергетическим ландшафтом задачи.
Как я писал подробнее в этой статье, в ходе работы когерентной машины Изинга амплитуда лазерной накачки a постепенно увеличивается, и когда она переходит через некоторый порог, коллективное состояние взаимодействующих оптических параметрических осцилляторов оказывается, в идеале, в глобальном минимуме энергии.
Если рассмотреть один осциллятор, то его энергетический ландшафт –ax² + x⁴ ведет себя как при фазовом переходе 2-го рода: при a < 0 у нас имеется единственный минимум x = 0, а при a > 0 происходит бифуркация на два минимума x = ±√a. В случае большого числа связанных осцилляторов происходит что-то похожее, но в многомерном и неупорядоченном варианте: изначально выпуклый вниз ландшафт, имеющий единственный минимум в нуле, при увеличении a постепенно уплощается, и на нем развивается множество локальных минимумов, среди которых постепенно выделяется единственный, ярко выраженный глобальный минимум.
Авторы исследуют эволюцию многомерного ландшафта при помощи метода реплик, теории случайных матриц и аппарата суперсимметрии. По итогам анализа, они выделяют несколько этапов:
1) При a < a_r ландшафт остается выпуклым вниз и имеет единственный минимум в нуле. Соответственно, когерентная машина Изинга как квантовая система остается, на фоне такого ландшафта, в более-менее хорошем вакуумном состоянии.
2) При a_r < a < a_t локальных минимумов становится уже много, но на самом деле их число субэкспоненциально по N – числу осцилляторов, и все они примерно одинаково неглубокие. Это проявление суперсимметрии – симметрии системы по отношению к превращению бозонов в фермионы и обратно – возникающей при анализе задачи методом реплик. Квантовое состояние когерентной машины Изинга при этом должно быть, по идее, сильно флуктуирующим вакуумом.
3) При a_t < a < a_g суперсимметрия нарушается. Это проявляется в том, что число локальных минимумов становится уже экспоненциальным по N, и в пределе N →∞ система приобретает ненулевую сложность (complexity) – энтропию, связанную со способностью застревать в одном из этих минимумов и говорящую о неопределенности коллективного состояния системы. При этом локальные минимумы перестают быть статистически эквивалентными: среди них появляются более мелкие и более глубокие, а самый глубокий из них становится глобальным.
Тем не менее, минимумы остаются маргинально устойчивыми: из каждого из них можно выйти с небольшими затратами энергии. И глобальный минимум тоже не очень-то глубок на фоне остальных. Можно предположить, что квантовое состояние машины при этом все еще сильно флуктуирует, но уже сосредотачивается вблизи глобального минимума – хотя и не макроскопически большой долей своей волновой функции.
4) Наконец, при a > a_g происходит так называемый переход жесткости (rigidity transition): глобальный минимум становится очень глубоким на фоне остальных, а выход из него стоит макроскопически большой энергии. Иными словами, спектр гессиана – то есть собственные значения матрицы вторых производных энергии по координатам ландшафта – в этой точке положителен и отделен от нуля конечной щелью. То есть колебания вблизи этой точки становятся «жесткими». Квантовое состояние машины Изинга при этом уже макроскопически концентрируется в глобальном минимуме.
На самом деле, таких «глобальных минимумов» может быть довольно много, и все они примерно одинаково глубоко и одинаково жесткие. С практической точки зрения, не столь уж важно, в какой из них мы попадем, потому что все они будут давать более-менее одинаково хорошие решения оптимизационной задачи. Еще один практический вывод, который делают авторы, состоит в том, что нет нужды повышать a выше a_g: на этом месте работу когерентной машины Изинга можно уже останавливать.
#стекла #нейронные_сети #оптимизация
Как я писал подробнее в этой статье, в ходе работы когерентной машины Изинга амплитуда лазерной накачки a постепенно увеличивается, и когда она переходит через некоторый порог, коллективное состояние взаимодействующих оптических параметрических осцилляторов оказывается, в идеале, в глобальном минимуме энергии.
Если рассмотреть один осциллятор, то его энергетический ландшафт –ax² + x⁴ ведет себя как при фазовом переходе 2-го рода: при a < 0 у нас имеется единственный минимум x = 0, а при a > 0 происходит бифуркация на два минимума x = ±√a. В случае большого числа связанных осцилляторов происходит что-то похожее, но в многомерном и неупорядоченном варианте: изначально выпуклый вниз ландшафт, имеющий единственный минимум в нуле, при увеличении a постепенно уплощается, и на нем развивается множество локальных минимумов, среди которых постепенно выделяется единственный, ярко выраженный глобальный минимум.
Авторы исследуют эволюцию многомерного ландшафта при помощи метода реплик, теории случайных матриц и аппарата суперсимметрии. По итогам анализа, они выделяют несколько этапов:
1) При a < a_r ландшафт остается выпуклым вниз и имеет единственный минимум в нуле. Соответственно, когерентная машина Изинга как квантовая система остается, на фоне такого ландшафта, в более-менее хорошем вакуумном состоянии.
2) При a_r < a < a_t локальных минимумов становится уже много, но на самом деле их число субэкспоненциально по N – числу осцилляторов, и все они примерно одинаково неглубокие. Это проявление суперсимметрии – симметрии системы по отношению к превращению бозонов в фермионы и обратно – возникающей при анализе задачи методом реплик. Квантовое состояние когерентной машины Изинга при этом должно быть, по идее, сильно флуктуирующим вакуумом.
3) При a_t < a < a_g суперсимметрия нарушается. Это проявляется в том, что число локальных минимумов становится уже экспоненциальным по N, и в пределе N →∞ система приобретает ненулевую сложность (complexity) – энтропию, связанную со способностью застревать в одном из этих минимумов и говорящую о неопределенности коллективного состояния системы. При этом локальные минимумы перестают быть статистически эквивалентными: среди них появляются более мелкие и более глубокие, а самый глубокий из них становится глобальным.
Тем не менее, минимумы остаются маргинально устойчивыми: из каждого из них можно выйти с небольшими затратами энергии. И глобальный минимум тоже не очень-то глубок на фоне остальных. Можно предположить, что квантовое состояние машины при этом все еще сильно флуктуирует, но уже сосредотачивается вблизи глобального минимума – хотя и не макроскопически большой долей своей волновой функции.
4) Наконец, при a > a_g происходит так называемый переход жесткости (rigidity transition): глобальный минимум становится очень глубоким на фоне остальных, а выход из него стоит макроскопически большой энергии. Иными словами, спектр гессиана – то есть собственные значения матрицы вторых производных энергии по координатам ландшафта – в этой точке положителен и отделен от нуля конечной щелью. То есть колебания вблизи этой точки становятся «жесткими». Квантовое состояние машины Изинга при этом уже макроскопически концентрируется в глобальном минимуме.
На самом деле, таких «глобальных минимумов» может быть довольно много, и все они примерно одинаково глубоко и одинаково жесткие. С практической точки зрения, не столь уж важно, в какой из них мы попадем, потому что все они будут давать более-менее одинаково хорошие решения оптимизационной задачи. Еще один практический вывод, который делают авторы, состоит в том, что нет нужды повышать a выше a_g: на этом месте работу когерентной машины Изинга можно уже останавливать.
#стекла #нейронные_сети #оптимизация
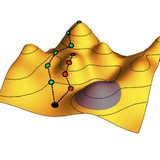
А вот иллюстрация из статьи из предыдущего поста, на которой можно видеть признаки описанной там эволюции потенциального ландшафта.
На графике сверху показаны типичные энергии критических точек ландшафта, где производная обращается в ноль. Среди них можно выделить локальные минимумы, а остальные – это либо седловые точки, либо локальные максимумы. Можно видеть, как при переходе накачки a через a_r на ландшафте постепенно развиваются минимумы, причем неглубокие: их энергия, в пределе N →∞, такая же, как у остальных критических точек. При пересечении второго порога a_t минимумы и остальные критические точки разделяются по энергиям, а при a > a_g глобальный минимум особенно сильно углубляется.
Диаграммы снизу иллюстрируют иерархию критических точек при a > a_g: чем дальше они от начала координат, тем ниже по энергии и тем ниже их индекс – число отрицательных собственных значений гессиана, то есть направленных вниз по энергии направлений на ландшафте.
#стекла #нейронные_сети #оптимизация
На графике сверху показаны типичные энергии критических точек ландшафта, где производная обращается в ноль. Среди них можно выделить локальные минимумы, а остальные – это либо седловые точки, либо локальные максимумы. Можно видеть, как при переходе накачки a через a_r на ландшафте постепенно развиваются минимумы, причем неглубокие: их энергия, в пределе N →∞, такая же, как у остальных критических точек. При пересечении второго порога a_t минимумы и остальные критические точки разделяются по энергиям, а при a > a_g глобальный минимум особенно сильно углубляется.
Диаграммы снизу иллюстрируют иерархию критических точек при a > a_g: чем дальше они от начала координат, тем ниже по энергии и тем ниже их индекс – число отрицательных собственных значений гессиана, то есть направленных вниз по энергии направлений на ландшафте.
#стекла #нейронные_сети #оптимизация
Интересная теоретическая работа, в которой предложена концепция перестраиваемых пространственно-временных метаповерхностей.
Пример такой метаповерхности – это показанный сверху массив анизотропных диэлектрических элементов, заранее выстроенный в определенный ориентационный узор. Накачка такого массива электромагнитной волной (или результатом интерференции двух волн) с волновым вектором β и частотой Ω позволяет, за счет эффекта Керра в диэлектрике, создавать соответствующую пространственно-временную модуляцию отклика модуляцию ~exp(iβr – iΩt) всей метаповерхности. А ориентационный узор элементов позволяет дополнительно модулировать и геометрическую фазу света, прошедшего через метаповерхность.
Управляемая зависимость отклика метаповерхности одновременно от координат, времени и поляризации позволяет запутывать прошедшие фотоны в пространстве их поляризаций, импульсов и энергий. Примеры матриц плотности таких гиперзапутанных фотонных состояний показаны на панелях (d), (e), (f).
#фотоника
Пример такой метаповерхности – это показанный сверху массив анизотропных диэлектрических элементов, заранее выстроенный в определенный ориентационный узор. Накачка такого массива электромагнитной волной (или результатом интерференции двух волн) с волновым вектором β и частотой Ω позволяет, за счет эффекта Керра в диэлектрике, создавать соответствующую пространственно-временную модуляцию отклика модуляцию ~exp(iβr – iΩt) всей метаповерхности. А ориентационный узор элементов позволяет дополнительно модулировать и геометрическую фазу света, прошедшего через метаповерхность.
Управляемая зависимость отклика метаповерхности одновременно от координат, времени и поляризации позволяет запутывать прошедшие фотоны в пространстве их поляризаций, импульсов и энергий. Примеры матриц плотности таких гиперзапутанных фотонных состояний показаны на панелях (d), (e), (f).
#фотоника
А вот еще на что способны пространственно-временные метаповерхности, предложенные в статье из предыдущего поста.
Здесь метаповерхность состоит из массива графеновых дисков, электромагнитный отклик которых модулируется в пространстве и времени при помощи накачки. Как результат, метаповерхность с модулируемой функцией отклика способна генерировать из вакуума фотоны – подобно осциллятору с модулируемыми параметрами, который может спонтанно раскачиваться. Это, по сути, разновидность динамического эффекта Казимира.
Фотоны из вакуума при этом генерируются в виде запутанных пар, причем оба фотона в паре имеют, вообще говоря, частоты. Диаграммы снизу показывают, как связаны между собой импульсы, частоты и интенсивности излучения фотонов таких генерируемых пар.
Авторы называли все это управляемым квантовым вакуумом (steered quantum vacuum).
#фотоника #графен
Здесь метаповерхность состоит из массива графеновых дисков, электромагнитный отклик которых модулируется в пространстве и времени при помощи накачки. Как результат, метаповерхность с модулируемой функцией отклика способна генерировать из вакуума фотоны – подобно осциллятору с модулируемыми параметрами, который может спонтанно раскачиваться. Это, по сути, разновидность динамического эффекта Казимира.
Фотоны из вакуума при этом генерируются в виде запутанных пар, причем оба фотона в паре имеют, вообще говоря, частоты. Диаграммы снизу показывают, как связаны между собой импульсы, частоты и интенсивности излучения фотонов таких генерируемых пар.
Авторы называли все это управляемым квантовым вакуумом (steered quantum vacuum).
#фотоника #графен
При вращении сосуда со сверхтекучей жидкостью ее нормальная компонента, как известно, должна увлекаться трением о стенки и, в конце концов, вращаться с той же скоростью, что и сам сосуд. Сверхтекучая же компонента, как показано на рисунке, вращаться может только в виде квантованных вихрей.
Картина усложняется тем обстоятельством, что и сами квантованные вихри, содержащие внутри себя нормальную компоненту, тоже увлекаются за сосудом и вращаются как целое. Поэтому вся сверхтекучая компонента может вращаться вместе с сосудом практически с той же угловой частотой Ω.
Тем не менее, в этом эксперименте было продемонстрировано «отвязывание» вихрей от вращающегося сосуда при понижении температуры. Как показано пиками на графике слева, скорости вращения вихревых сгустков меньше, чем Ω. А график справа показывает, как она становится все меньше при снижении температуры. Таким образом, при T → 0 вихревые линии вращаются все слабее и восстанавливается идеальная картинка «из учебника», показанная сверху.
#сверхтекучесть
Картина усложняется тем обстоятельством, что и сами квантованные вихри, содержащие внутри себя нормальную компоненту, тоже увлекаются за сосудом и вращаются как целое. Поэтому вся сверхтекучая компонента может вращаться вместе с сосудом практически с той же угловой частотой Ω.
Тем не менее, в этом эксперименте было продемонстрировано «отвязывание» вихрей от вращающегося сосуда при понижении температуры. Как показано пиками на графике слева, скорости вращения вихревых сгустков меньше, чем Ω. А график справа показывает, как она становится все меньше при снижении температуры. Таким образом, при T → 0 вихревые линии вращаются все слабее и восстанавливается идеальная картинка «из учебника», показанная сверху.
#сверхтекучесть
В методе функционала плотности (DFT) электронная плотность n(r) называется v-представимой (v-representable), если она, в принципе, может быть электронной плотностью в основном состоянии многоэлектронной системы, помещенной в какой-либо внешний потенциал v(r). Какие именно функции n(r) являются v-представимыми, а какими не являются – это важный вопрос для теоретического обоснования DFT, поскольку функционал плотности может быть физически определен только на классе v-представимых функций n(r).
В этой работе рассмотрен вопрос о v-представимости электронной плотности для нестационарной задачи линейного отклика. А именно, любая ли электронная плотность n₁(r)exp(–iωt), осциллирующая с частотой ω, может быть представлена как линейный отклик многоэлектронной системы на осциллирующий внешний потенциал v₁(r)exp(–iωt)?
На этот вопрос авторы дают следующий ответ: любая осциллирующая электронная плотность является v-представимой лишь в том случае, когда частота ее колебаний ω не превышает наименьшую энергию возбуждения ω_min. При ω > ω_min некоторые профили плотности n₁(r)exp(–iωt) уже не могут быть результатом отклика на внешний потенциал. Более того, могут существовать некоторые изолированные частоты, при которых частотах почти любые профили плотности не являются v-представимыми. Это обстоятельство накладывает определенные теоретические ограничения не нестационарный вариант DFT, да и в целом на теорию линейного отклика.
#твердое_тело #квантовая_механика
В этой работе рассмотрен вопрос о v-представимости электронной плотности для нестационарной задачи линейного отклика. А именно, любая ли электронная плотность n₁(r)exp(–iωt), осциллирующая с частотой ω, может быть представлена как линейный отклик многоэлектронной системы на осциллирующий внешний потенциал v₁(r)exp(–iωt)?
На этот вопрос авторы дают следующий ответ: любая осциллирующая электронная плотность является v-представимой лишь в том случае, когда частота ее колебаний ω не превышает наименьшую энергию возбуждения ω_min. При ω > ω_min некоторые профили плотности n₁(r)exp(–iωt) уже не могут быть результатом отклика на внешний потенциал. Более того, могут существовать некоторые изолированные частоты, при которых частотах почти любые профили плотности не являются v-представимыми. Это обстоятельство накладывает определенные теоретические ограничения не нестационарный вариант DFT, да и в целом на теорию линейного отклика.
#твердое_тело #квантовая_механика
Physical Review A
Frequency-dependent v-representability in density-functional theory
In density-functional theory (DFT) of the ground state, a density distribution ${n}_{o}$(r) is called v-representable (VR) if it is the ground-state density in some external potential. [It is known that not all ``reasonable'' ${n}_{0}$(r) are VR.] In DFT…
Неплохая современная (2007 года) книга по релятивистской квантовой теории поля, автором которой является Марк Средницкий – физик, более всего известный своей гипотезой термализации собственных состояний (eigenstate thermalization hypothesis).
Вот достоинства книги, которые мне удалось заметить:
● Все математические выкладки подробно и последовательно выводятся, действие за действием.
● Книга разбита на разделы, посвященные полям со спином 0 (скалярным частицам), 1/2 (фермионам) и 1 (фотонам и массивным бозонам), причем для всех этих случаев дается единообразное рассмотрение: квантование поля, функциональные интегралы, вывод фейнмановских правил, расчет петлевых и вершинных диаграмм, перенормировки и т.д.
● В отличие от некоторых других книг, где вопросы перенормировок оставляются на потом, в разделы «со звездочкой», здесь автор с самого начала подробно обсуждает вопрос перенормируемости теорий, показывает перенормировки на конкретных примерах и обсуждает соответствующие бета-функции.
● Отдельное место уделяется квантовым аномалиям – особенно популярным в последние годы в связи с исследованиями топологических материалов.
● Начиная с основ, автор в конце концов переходит к неабелевым калибровочным теориям Янга-Миллса, а затем – и к стандартной модели как таковой, последовательно описывая все ее ингредиенты.
В общем, как мне показалось, эта книга может быть неплохим пособием для полноценного изучения квантовой теории поля.
#электродинамика #элементарные_частицы #ядерная_физика
Вот достоинства книги, которые мне удалось заметить:
● Все математические выкладки подробно и последовательно выводятся, действие за действием.
● Книга разбита на разделы, посвященные полям со спином 0 (скалярным частицам), 1/2 (фермионам) и 1 (фотонам и массивным бозонам), причем для всех этих случаев дается единообразное рассмотрение: квантование поля, функциональные интегралы, вывод фейнмановских правил, расчет петлевых и вершинных диаграмм, перенормировки и т.д.
● В отличие от некоторых других книг, где вопросы перенормировок оставляются на потом, в разделы «со звездочкой», здесь автор с самого начала подробно обсуждает вопрос перенормируемости теорий, показывает перенормировки на конкретных примерах и обсуждает соответствующие бета-функции.
● Отдельное место уделяется квантовым аномалиям – особенно популярным в последние годы в связи с исследованиями топологических материалов.
● Начиная с основ, автор в конце концов переходит к неабелевым калибровочным теориям Янга-Миллса, а затем – и к стандартной модели как таковой, последовательно описывая все ее ингредиенты.
В общем, как мне показалось, эта книга может быть неплохим пособием для полноценного изучения квантовой теории поля.
#электродинамика #элементарные_частицы #ядерная_физика
❤1😱1
Алгоритм Шора позволяет разложить большое число N на простые сомножители за O(ln N) операций на квантовом компьютере. А в этой работе был предложен другой алгоритм, работающий значительно быстрее (и гораздо более простой!): в идеале, для разложения числа на простые сомножители ему требуется всего k операций, где k – число простых сомножителей, независимо от их кратности.
Алгоритм работает следующим образом. Составим квантовую систему с гамильтонианом H, состоящим из двух слагаемых H = H₁ + H₂. При этом собственные значения H₁ имеют вид ln pᵢ, то есть это логарифмы простых чисел pᵢ, а собственные значения H₂ – это ln m, то есть просто логарифмы идущих подряд целых чисел; pᵢ и m должны быть в диапазоне от 2 до какого-то верхнего предела, не меньшего √N.
Полный гамильтониан системы H = H₁ + H₂ имеет собственные значения ln pᵢ + ln m и соответствующие собственные функции |ln pᵢ>|ln m>. Для разложения числа N на простые сомножители мы должны приготовить систему в собственном состоянии гамильтониана |ln N>. Ключевой момент в том, что, вообще говоря, этот вектор будет k-кратно вырожден, потому N можно k разными способами представить в виде произведения каждого из его простых сомножителей pᵢ и какого-то другого целого числа. К примеру, если N = p₁(p₂)², то его можно представить как N = p₁×(p₂)² либо как N = (p₁p₂)×p₂.
Поэтому приготовленное состояние |ln N> будет некоторой суперпозицией собственных векторов гамильтониана H с одинаковыми энергиями, имеющих вид |ln pᵢ>|ln m>, где pᵢ – только те простые сомножители, которые входят в число N. Если над этим вектором мы произведем операцию измерения оператора H₁, то мы получим одно из чисел ln pᵢ в качестве результата измерения. Все, что нам остается сделать – это разделить N на pᵢ на классическом компьютере и повторять все действия до тех пор, пока мы не найдем все простые сомножители.
Главная трудность этого алгоритма – в реализации гамильтониана H₁, имеющего уровни энергии в виде логарифма простых чисел. Чтобы создать его на основе ln√N кубитов, требуется большое число дальних взаимодействий между ними, что выглядит нереалистичным. Авторы предлагают аналоговую реализацию такого гамильтониана на основе одномерной системы H₁ = p²/2m + V₁(x), потенциальную энергию V₁(x) которой можно построить в явном виде, используя аппарат суперсимметричной квантовой механики. А именно, для нахождения потенциала нужно решить систему √N нелинейных дифференциальных уравнений – а эта вспомогательная задача сама по себе может быть быстро решена на квантовом компьютере за ln√N вычислительных шагов.
Интересно сравнить новый алгоритм с более традиционным алгоритмом Шора:
● Алгоритм Шора требует порядка ln N операций и может выполняться, в принципе, на произвольных цифровых квантовых компьютерах, способных производить универсальный набор одно- и двухкубитных операций.
● Новый алгоритм требует гораздо меньшего числа операций (всего 2, если число N состоит из двух простых сомножителей), но для его работы нужен квантовый компьютер с заранее приготовленной архитектурой сложно устроенного гамильтониана H₁. С другой стороны, если мы один раз создали эту архитектуру, далее ее можно использовать сколько угодно раз для разложения все больших чисел, в то время как алгоритм Шора должен каждый раз запускаться с нуля.
#квантовые_вычисления #отвал_башки
Алгоритм работает следующим образом. Составим квантовую систему с гамильтонианом H, состоящим из двух слагаемых H = H₁ + H₂. При этом собственные значения H₁ имеют вид ln pᵢ, то есть это логарифмы простых чисел pᵢ, а собственные значения H₂ – это ln m, то есть просто логарифмы идущих подряд целых чисел; pᵢ и m должны быть в диапазоне от 2 до какого-то верхнего предела, не меньшего √N.
Полный гамильтониан системы H = H₁ + H₂ имеет собственные значения ln pᵢ + ln m и соответствующие собственные функции |ln pᵢ>|ln m>. Для разложения числа N на простые сомножители мы должны приготовить систему в собственном состоянии гамильтониана |ln N>. Ключевой момент в том, что, вообще говоря, этот вектор будет k-кратно вырожден, потому N можно k разными способами представить в виде произведения каждого из его простых сомножителей pᵢ и какого-то другого целого числа. К примеру, если N = p₁(p₂)², то его можно представить как N = p₁×(p₂)² либо как N = (p₁p₂)×p₂.
Поэтому приготовленное состояние |ln N> будет некоторой суперпозицией собственных векторов гамильтониана H с одинаковыми энергиями, имеющих вид |ln pᵢ>|ln m>, где pᵢ – только те простые сомножители, которые входят в число N. Если над этим вектором мы произведем операцию измерения оператора H₁, то мы получим одно из чисел ln pᵢ в качестве результата измерения. Все, что нам остается сделать – это разделить N на pᵢ на классическом компьютере и повторять все действия до тех пор, пока мы не найдем все простые сомножители.
Главная трудность этого алгоритма – в реализации гамильтониана H₁, имеющего уровни энергии в виде логарифма простых чисел. Чтобы создать его на основе ln√N кубитов, требуется большое число дальних взаимодействий между ними, что выглядит нереалистичным. Авторы предлагают аналоговую реализацию такого гамильтониана на основе одномерной системы H₁ = p²/2m + V₁(x), потенциальную энергию V₁(x) которой можно построить в явном виде, используя аппарат суперсимметричной квантовой механики. А именно, для нахождения потенциала нужно решить систему √N нелинейных дифференциальных уравнений – а эта вспомогательная задача сама по себе может быть быстро решена на квантовом компьютере за ln√N вычислительных шагов.
Интересно сравнить новый алгоритм с более традиционным алгоритмом Шора:
● Алгоритм Шора требует порядка ln N операций и может выполняться, в принципе, на произвольных цифровых квантовых компьютерах, способных производить универсальный набор одно- и двухкубитных операций.
● Новый алгоритм требует гораздо меньшего числа операций (всего 2, если число N состоит из двух простых сомножителей), но для его работы нужен квантовый компьютер с заранее приготовленной архитектурой сложно устроенного гамильтониана H₁. С другой стороны, если мы один раз создали эту архитектуру, далее ее можно использовать сколько угодно раз для разложения все больших чисел, в то время как алгоритм Шора должен каждый раз запускаться с нуля.
#квантовые_вычисления #отвал_башки
arXiv.org
Integer Factorization by Quantum Measurements
Quantum algorithms are at the heart of the ongoing efforts to use quantum mechanics to solve computational problems unsolvable on ordinary classical computers. Their common feature is the use of...
🔥6
В этой работе было обнаружено своеобразное сверхпроводящее диссипативное состояние цинковой квантовой нити, сочетающее сверхпроводимость и диссипацию энергии.
На графике слева показано, в чем проявляется это состояние: на зависимости сопротивления (или падения напряжения V при фиксированном токе) от температуры вместо одной ступеньки, на которой оно падает до нуля при T = T_c, наблюдаются две ступеньки со странным промежуточным плато, где сопротивление не зависит от температуры, но и не равно нулю. Измерение V с временным разрешением показывает, что на плато мы видим лишь его среднюю величину, а на самом деле система хаотично переключается между сверхпроводящим и нормальным состояниями.
Авторы предполагают, что диссипативное сверхпроводящее состояние обусловлено формированием участка с проскальзыванием фазы посреди нанонити, как показано на рисунке снизу. Между этим участком и обоими контактами циркулируют электроны и андреевски отраженные дырки, образуя диссипативный нормальный ток.
#сверхпроводимость
На графике слева показано, в чем проявляется это состояние: на зависимости сопротивления (или падения напряжения V при фиксированном токе) от температуры вместо одной ступеньки, на которой оно падает до нуля при T = T_c, наблюдаются две ступеньки со странным промежуточным плато, где сопротивление не зависит от температуры, но и не равно нулю. Измерение V с временным разрешением показывает, что на плато мы видим лишь его среднюю величину, а на самом деле система хаотично переключается между сверхпроводящим и нормальным состояниями.
Авторы предполагают, что диссипативное сверхпроводящее состояние обусловлено формированием участка с проскальзыванием фазы посреди нанонити, как показано на рисунке снизу. Между этим участком и обоими контактами циркулируют электроны и андреевски отраженные дырки, образуя диссипативный нормальный ток.
#сверхпроводимость
👀1
Несколько лет назад считалось, что самый обычный висмут является трехмерным топологическим изолятором, но впоследствии выяснилось, что это не так. Тем не менее, недавние эксперименты показали, что висмут таки является топологически нетривиальным материалом – но не обычным, а топологическим изолятором высшего порядка.
Как я писал раньше, топологические изоляторы высшего порядка должны, вместо краевых или поверхностных мод, обладать корневыми (в двумерном случае) или петельными (в трехмерном случае) состояниями внутри щели.
Пример одномерных петельных состояний (hinge states), существующих вдоль стыков граней кристалла висмута, показан на рисунке. При сканировании островка висмута (панель (a)) вдоль (e) или поперек (d) стыка мы видим в туннельном спектре состояния не энергии около 100 мэВ внутри щели. В пространстве эти состояния привязаны именно к одномерному стыку.
#топологические_материалы
Как я писал раньше, топологические изоляторы высшего порядка должны, вместо краевых или поверхностных мод, обладать корневыми (в двумерном случае) или петельными (в трехмерном случае) состояниями внутри щели.
Пример одномерных петельных состояний (hinge states), существующих вдоль стыков граней кристалла висмута, показан на рисунке. При сканировании островка висмута (панель (a)) вдоль (e) или поперек (d) стыка мы видим в туннельном спектре состояния не энергии около 100 мэВ внутри щели. В пространстве эти состояния привязаны именно к одномерному стыку.
#топологические_материалы
Отлично написанный небольшой обзор о связанных состояниях в континууме, в котором довольно понятно объясняется механизм возникновения таких состояний и приводится множество примеров их реализации в электромагнитных, акустических, электрических и других системах.
В отличие от обычных связанных состояний, располагающихся за пределами непрерывного спектра, и квазисвязанных состояний (долгоживущих резонансов), находящихся в нем, но постепенно распадающихся утеканием волны на бесконечность, связанные состояния в континууме одновременно и находятся внутри непрерывного спектра по энергии, и полностью локализованы.
Первый пример связанных состояний в континууме был предложен фон Нейманом и Вигнером: как показано на рисунке, зависящий от r потенциал в трехмерном пространстве создает волновую функцию, убывающую на бесконечности. Такой потенциал работает как аналог брэгговского зеркала, заставляя уходящие на бесконечность волны деструктивно интерферировать между собой.
#электродинамика #фотоника #квантовая_механика
В отличие от обычных связанных состояний, располагающихся за пределами непрерывного спектра, и квазисвязанных состояний (долгоживущих резонансов), находящихся в нем, но постепенно распадающихся утеканием волны на бесконечность, связанные состояния в континууме одновременно и находятся внутри непрерывного спектра по энергии, и полностью локализованы.
Первый пример связанных состояний в континууме был предложен фон Нейманом и Вигнером: как показано на рисунке, зависящий от r потенциал в трехмерном пространстве создает волновую функцию, убывающую на бесконечности. Такой потенциал работает как аналог брэгговского зеркала, заставляя уходящие на бесконечность волны деструктивно интерферировать между собой.
#электродинамика #фотоника #квантовая_механика
👍2
Вот пара простых примеров связанных состояний в континууме, наблюдавшихся в экспериментах.
Слева на рисунке показан плоский акустический волновод, в центре которого располагается небольшая вставка-препятствие. Протяженные состояния континуума, которые распространяются на бесконечность в обе стороны, обладают четным по вертикали профилем колебаний давления. Связанное же состояние в континууме имеет нечетный профиль, поэтому, в силу симметрии, не может связываться с протяженными состояниями.
Справа показан другой пример: плоский фотонный кристалл в виде массива отверстий в слое диэлектрика. Протяженные состояния, утекающие на бесконечность, должны обладать электрическим и магнитным полями, меняющими знак при повороте на 180° в плоскости кристалла. А связанные состояния в континууме (их здесь целый набор) имеют профили поля, не меняющиеся при таких поворотах, и поэтому не связываются с излучением дальнего поля из-за несовместимости симметрий.
#электродинамика #фотоника #квантовая_механика
Слева на рисунке показан плоский акустический волновод, в центре которого располагается небольшая вставка-препятствие. Протяженные состояния континуума, которые распространяются на бесконечность в обе стороны, обладают четным по вертикали профилем колебаний давления. Связанное же состояние в континууме имеет нечетный профиль, поэтому, в силу симметрии, не может связываться с протяженными состояниями.
Справа показан другой пример: плоский фотонный кристалл в виде массива отверстий в слое диэлектрика. Протяженные состояния, утекающие на бесконечность, должны обладать электрическим и магнитным полями, меняющими знак при повороте на 180° в плоскости кристалла. А связанные состояния в континууме (их здесь целый набор) имеют профили поля, не меняющиеся при таких поворотах, и поэтому не связываются с излучением дальнего поля из-за несовместимости симметрий.
#электродинамика #фотоника #квантовая_механика
👍3
Еще несколько фактов о связанных состояниях в континууме:
● Они не могут существовать в компактных структурах: то есть в системах, где либо удерживающий потенциал (в квантовомеханическом случае), либо диэлектрические структуры (в электромагнитном случае) ограничены в пространстве во всех измерениях. Это доказывается математически состыковкой граничных условий на краю такой структуры. Для существования связанных состояний в континууме нужно, чтобы поддерживающая их структура была протяженной, то есть простиралась формально до бесконечности. Или нужна какая-нибудь экзотика: например, многочастичность либо волновое уравнение, отличное от уравнений Шредингера или Максвелла.
● Связанные состояния в континууме можно разделить на несколько типов:
1) Симметрийно-защищенные – состояния, обладающие симметрией, несовместимой с модами континуума и поэтому «отвязанных» от него. Их примеры можно найти в предыдущем посте.
2) Состояния типа Фабри-Перо: простейший пример здесь – два параллельных брэгговских зеркала, которые становятся идеально отражающими лишь при определенной частоте, на которой электромагнитная мода и ловится между зеркалами, отцепляясь от континуума мод снаружи.
В более общем случае можно представить себе два связанных осциллятора, в которых, из-за их связи, образуются две гибридизованные моды. В предыдущем примере это были две волны, распространяющихся между зеркалами влево и вправо, связанные между собой отражением и с дополнительным набегом фазы при пересечении толщи резонатора. Скорости распада двух исходных мод при образовании гибридизованных состояний складываются и вычитаются (опять-таки, с дополнительным набегом фаз), и может случиться так, что при вычитании с правильной относительной фазой скорость распада одного из гибридизованных состояний окажется равной нулю. Это и будет связанное состояние в континууме.
3) Состояния Фридриха-Уинтгена – их можно считать частным случаем состояний Фабри-Перо. Они возникают в фотонных кристаллах при пересечении дисперсий двух мод различных симметрий. При таком пересечении одна из гибридизованных мод оказывается связанным состоянием в континууме с нулевой скоростью распада, а вся суммарная скорость распада двух исходных мод навешивается на вторую гибридизованную моду.
● Связанные состояния в континууме дают хорошую и, иногда, довольно устойчивую локализацию волн, поэтому могут использоваться как резонатор для лазеров, а также для создания направленных «волноводов» для электромагнитных и акустических волн.
● В некоторых конструкциях связанные состояния в континууме, наоборот, могут требовать очень тонкой подстройки параметров системы и поэтому очень чувствительны к их малым изменениям. Так можно создавать чувствительные сенсоры – например, обнаруживающие нужные вещества и молекулы по изменениям диэлектрического окружения системы.
● Благодаря тому, что связанные состояния в континууме существуют либо при четко определенных частотах, либо в узких спектральных диапазонах, они могут использоваться и для создания частотных фильтров.
#электродинамика #фотоника #квантовая_механика
● Они не могут существовать в компактных структурах: то есть в системах, где либо удерживающий потенциал (в квантовомеханическом случае), либо диэлектрические структуры (в электромагнитном случае) ограничены в пространстве во всех измерениях. Это доказывается математически состыковкой граничных условий на краю такой структуры. Для существования связанных состояний в континууме нужно, чтобы поддерживающая их структура была протяженной, то есть простиралась формально до бесконечности. Или нужна какая-нибудь экзотика: например, многочастичность либо волновое уравнение, отличное от уравнений Шредингера или Максвелла.
● Связанные состояния в континууме можно разделить на несколько типов:
1) Симметрийно-защищенные – состояния, обладающие симметрией, несовместимой с модами континуума и поэтому «отвязанных» от него. Их примеры можно найти в предыдущем посте.
2) Состояния типа Фабри-Перо: простейший пример здесь – два параллельных брэгговских зеркала, которые становятся идеально отражающими лишь при определенной частоте, на которой электромагнитная мода и ловится между зеркалами, отцепляясь от континуума мод снаружи.
В более общем случае можно представить себе два связанных осциллятора, в которых, из-за их связи, образуются две гибридизованные моды. В предыдущем примере это были две волны, распространяющихся между зеркалами влево и вправо, связанные между собой отражением и с дополнительным набегом фазы при пересечении толщи резонатора. Скорости распада двух исходных мод при образовании гибридизованных состояний складываются и вычитаются (опять-таки, с дополнительным набегом фаз), и может случиться так, что при вычитании с правильной относительной фазой скорость распада одного из гибридизованных состояний окажется равной нулю. Это и будет связанное состояние в континууме.
3) Состояния Фридриха-Уинтгена – их можно считать частным случаем состояний Фабри-Перо. Они возникают в фотонных кристаллах при пересечении дисперсий двух мод различных симметрий. При таком пересечении одна из гибридизованных мод оказывается связанным состоянием в континууме с нулевой скоростью распада, а вся суммарная скорость распада двух исходных мод навешивается на вторую гибридизованную моду.
● Связанные состояния в континууме дают хорошую и, иногда, довольно устойчивую локализацию волн, поэтому могут использоваться как резонатор для лазеров, а также для создания направленных «волноводов» для электромагнитных и акустических волн.
● В некоторых конструкциях связанные состояния в континууме, наоборот, могут требовать очень тонкой подстройки параметров системы и поэтому очень чувствительны к их малым изменениям. Так можно создавать чувствительные сенсоры – например, обнаруживающие нужные вещества и молекулы по изменениям диэлектрического окружения системы.
● Благодаря тому, что связанные состояния в континууме существуют либо при четко определенных частотах, либо в узких спектральных диапазонах, они могут использоваться и для создания частотных фильтров.
#электродинамика #фотоника #квантовая_механика
Nature
Bound states in the continuum
Nature Reviews Materials - The fascinating wave phenomenon of ‘bound states in the continuum’ spans different material and wave systems, including electron, electromagnetic and...
❤2
А вот более современный и обстоятельный обзор о связанных состояниях в континууме для электромагнитных волн в диэлектрических, металлических и гибридных структурах. В отличие от предыдущего обзора, он направлен уже не на объяснения принципов, а на перечисление того, что сделано в этой области исследований в последние годы. И она действительно невероятно быстро развивается.
Авторы описывают основные реализации электромагнитных связанных состояний в континууме: фотонные кристаллы в виде двумерных периодических структур (это либо тонкий слой металла или диэлектрика, либо что-то, изготовленное или даже нацарапанное на поверхности трехмерного материала), трехмерные слоистые структуры и одномерные нити.
Подробно описываются и возможные их применения: лазерная генерация, направление излучения в нужную сторону, сенсоры, создание киральных лучей и структурированного света, переключатели, локальное усиление поля и нелинейная генерация гармоник.
#фотоника #электродинамика
Авторы описывают основные реализации электромагнитных связанных состояний в континууме: фотонные кристаллы в виде двумерных периодических структур (это либо тонкий слой металла или диэлектрика, либо что-то, изготовленное или даже нацарапанное на поверхности трехмерного материала), трехмерные слоистые структуры и одномерные нити.
Подробно описываются и возможные их применения: лазерная генерация, направление излучения в нужную сторону, сенсоры, создание киральных лучей и структурированного света, переключатели, локальное усиление поля и нелинейная генерация гармоник.
#фотоника #электродинамика
👍2
Раз уж сегодня у нас день связанных состояний в континууме, покажу еще один интересный факт.
На рисунке показан двумерный фотонный кристалл, в котором образуются связанные состояния в континууме, показанные пиками добротности на диаграмме сверху: одно симметрийно-защищенное при k = 0 и еще 4 состояния Фридриха-Уинтгена при k ≠ 0.
Оказывается, все они являются топологическими дефектами для поля линейной поляризации света, прошедшего через кристалл и детектируемого в дальнем поле. Симметрийно-защищенное состояние является вихрем заряда –1, состояния Фридриха-Уинтгена – вихрями заряда +1. Эти вихри образуются на пересечении зеленых и красных линий, где зануляются, соответственно E_x и E_y – поэтому в таких точках весь вектор E в дальнем поле обращается в ноль.
Из-за топологической нетривиальности, вихри оказываются весьма устойчивыми к малым изменениям параметров системы. Но сильным изменением параметров два вихря зарядов +1 и –1 можно заставить аннигилировать, как показано снизу.
#фотоника #электродинамика
На рисунке показан двумерный фотонный кристалл, в котором образуются связанные состояния в континууме, показанные пиками добротности на диаграмме сверху: одно симметрийно-защищенное при k = 0 и еще 4 состояния Фридриха-Уинтгена при k ≠ 0.
Оказывается, все они являются топологическими дефектами для поля линейной поляризации света, прошедшего через кристалл и детектируемого в дальнем поле. Симметрийно-защищенное состояние является вихрем заряда –1, состояния Фридриха-Уинтгена – вихрями заряда +1. Эти вихри образуются на пересечении зеленых и красных линий, где зануляются, соответственно E_x и E_y – поэтому в таких точках весь вектор E в дальнем поле обращается в ноль.
Из-за топологической нетривиальности, вихри оказываются весьма устойчивыми к малым изменениям параметров системы. Но сильным изменением параметров два вихря зарядов +1 и –1 можно заставить аннигилировать, как показано снизу.
#фотоника #электродинамика
Неопределенность результатов квантового измерения может использоваться для генерации истинно случайных чисел – и действительно, уже давно существуют пусть и не самые быстрые, но хорошие квантовые генераторы случайных чисел. В этой же работе рассматривается более амбициозная задача: можно ли при помощи квантовых эффектов организовать не зависящую от устройства сертифицированную генерацию истинно случайных чисел?
Под такой генерацией имеется в виду следующее:
1) Генерируемые числа полностью случайны, они никак не скоррелированы между собой ни в каких комбинациях.
2) Генерируемые числа устойчивы к враждебным атакам – это означает, что никакой внешний наблюдатель, подчиняющийся законам физики, не сможет их предугадать, независимо от своей вычислительной мощности.
3) Алгоритм генерации должен быть универсальным: надежность его работы не должна зависеть от архитектуры устройства, на котором он запускается.
Второй пункт особенно важен, если мы используем случайные числа для шифрования или для выбора стратегии в соревновательных играх. Пример чисел, полностью случайных (удовлетворяющих 1-му требованию), но уязвимых с точки зрения информационной безопасности, иллюстрируется «атакой при помощи флешки». Представим себе, что провайдер случайных чисел генерирует последовательность таких чисел, записывает их на флешку и продает потребителю. С точки зрения потребителя, это хорошие случайные числа, которые успешно пройдут все статистические тесты. Но проблема в том, что все они известны провайдеру, который, пользуясь этим знанием, может предпринять против потребителя враждебную атаку.
Предлагаемый авторами алгоритм, удовлетворяющий всем трем условиям, основывается на квантовой запутанности и моногамии квантовых корреляций. Для его работы нужны две квантовые системы 1 и 2, которые на каждом шаге генерации приводятся в состояние квантовой запутанности. Затем, на основе параметров измерений x₁ и x₂, которые можно менять по желанию, каждая система выдает результаты измерения a₁ и a₂. Для того, чтобы убедиться в сертифицированной случайности чисел, получаемых в результате постпроцессинга последовательности пар a₁ и a₂, нужно, чтобы условная вероятность P(a₁a₂|x₁x₂) нарушала неравенство Белла – а именно, некоторая сумма всех P(a₁a₂|x₁x₂) с коэффициентами, зависящими от аргументов, должна превышать максимальный предел, достижимый классически скоррелированным состоянием систем 1 и 2.
Если неравенство Белла нарушается – то есть системы 1 и 2 находятся в квантово запутанном состоянии – значит, наш генератор случайных чисел действительно сертифицирован. Причиной этому служит моногамия квантовых корреляций: если системы 1 и 2 максимально квантово запутаны между собой, то они не могут быть квантово запутаны с чем-либо еще – в том числе, и с предполагаемым злоумышленником. Следовательно, никто не может знать заранее, какими эти числа получатся.
На самом деле это, конечно, вопрос количественный: системы 1 и 2 могут быть запутаны между собой лишь частично, а частично – со злоумышленником, так что неравенство Белла будет нарушаться, но достаточно слабо. Тем не менее, даже такая ситуация поддается контролю. Авторы показывают, что если мы к примеру, считаем на основе статистики P(a₁a₂|x₁x₂) параметр Клаузера-Хорна-Шимони-Хольта, то превышение им значения 2 свидетельствует, как минимум, о существовании неклассических корреляций между двумя системами. Если этот параметр превышает 2√2, то классический злоумышленник не сможет предсказать наши случайные числа – для этого он должен быть существенно квантовым. Если же этот параметр достигает 4, то наши числа будут недоступны для предсказания любому злоумышленнику, неспособному передавать сигналы быстрее скорости света.
#квантовая_механика #квантовые_вычисления
Под такой генерацией имеется в виду следующее:
1) Генерируемые числа полностью случайны, они никак не скоррелированы между собой ни в каких комбинациях.
2) Генерируемые числа устойчивы к враждебным атакам – это означает, что никакой внешний наблюдатель, подчиняющийся законам физики, не сможет их предугадать, независимо от своей вычислительной мощности.
3) Алгоритм генерации должен быть универсальным: надежность его работы не должна зависеть от архитектуры устройства, на котором он запускается.
Второй пункт особенно важен, если мы используем случайные числа для шифрования или для выбора стратегии в соревновательных играх. Пример чисел, полностью случайных (удовлетворяющих 1-му требованию), но уязвимых с точки зрения информационной безопасности, иллюстрируется «атакой при помощи флешки». Представим себе, что провайдер случайных чисел генерирует последовательность таких чисел, записывает их на флешку и продает потребителю. С точки зрения потребителя, это хорошие случайные числа, которые успешно пройдут все статистические тесты. Но проблема в том, что все они известны провайдеру, который, пользуясь этим знанием, может предпринять против потребителя враждебную атаку.
Предлагаемый авторами алгоритм, удовлетворяющий всем трем условиям, основывается на квантовой запутанности и моногамии квантовых корреляций. Для его работы нужны две квантовые системы 1 и 2, которые на каждом шаге генерации приводятся в состояние квантовой запутанности. Затем, на основе параметров измерений x₁ и x₂, которые можно менять по желанию, каждая система выдает результаты измерения a₁ и a₂. Для того, чтобы убедиться в сертифицированной случайности чисел, получаемых в результате постпроцессинга последовательности пар a₁ и a₂, нужно, чтобы условная вероятность P(a₁a₂|x₁x₂) нарушала неравенство Белла – а именно, некоторая сумма всех P(a₁a₂|x₁x₂) с коэффициентами, зависящими от аргументов, должна превышать максимальный предел, достижимый классически скоррелированным состоянием систем 1 и 2.
Если неравенство Белла нарушается – то есть системы 1 и 2 находятся в квантово запутанном состоянии – значит, наш генератор случайных чисел действительно сертифицирован. Причиной этому служит моногамия квантовых корреляций: если системы 1 и 2 максимально квантово запутаны между собой, то они не могут быть квантово запутаны с чем-либо еще – в том числе, и с предполагаемым злоумышленником. Следовательно, никто не может знать заранее, какими эти числа получатся.
На самом деле это, конечно, вопрос количественный: системы 1 и 2 могут быть запутаны между собой лишь частично, а частично – со злоумышленником, так что неравенство Белла будет нарушаться, но достаточно слабо. Тем не менее, даже такая ситуация поддается контролю. Авторы показывают, что если мы к примеру, считаем на основе статистики P(a₁a₂|x₁x₂) параметр Клаузера-Хорна-Шимони-Хольта, то превышение им значения 2 свидетельствует, как минимум, о существовании неклассических корреляций между двумя системами. Если этот параметр превышает 2√2, то классический злоумышленник не сможет предсказать наши случайные числа – для этого он должен быть существенно квантовым. Если же этот параметр достигает 4, то наши числа будут недоступны для предсказания любому злоумышленнику, неспособному передавать сигналы быстрее скорости света.
#квантовая_механика #квантовые_вычисления
Nature
Certified randomness in quantum physics
Nature - For centuries the question of whether the world is deterministic—where every existing state of affairs is the inevitable consequence of previous states of affairs—or random was...
👍2