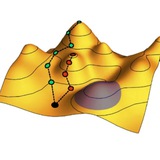
А вот еще один эксперимент с наблюдением исключительных точек – на этот раз, в экситон-плазмонной системе.

Плазмоны образуются на поверхности серебряной подложки, где вырезан массив наноканавок. Интервал между канавками медленно меняется вдоль образца, так что исследование разных его участков дает возможность медленно менять частоту плазмона, плавно проходя через исключительную точку. Второй компонент системы – это слой двумерного WS₂, лежащего на подложке сверху, экситоны которого гибридизуются с плазмонами.

Получается двухуровневая неэрмитова система с исключительной точкой, в которой один энергетический уровень расщепляется на два, расходящихся как квадратный корень расстройки между частотами экситона и плазмона. Экспериментальные графики подтверждают такое поведение спектральных линий.

Корневая зависимость, производная которой расходится в точке бифуркации, делают систему очень чувствительной к изменениям параметров – этим исключительные точки интересны на практике.

#неэрмитовы_системы #плазмоны

В последние годы становятся популярными исследования химических реакций в оптической полости: оказывается, квантование электромагнитных мод в ограниченной геометрии заметно модифицирует свойства молекул и влияет на ход некоторых химических реакций.

В этой работе рассмотрен пример такой модификации. Авторы численно решили уравнение Шредингера для молекулы HD⁺, состоящей из трех частиц, отталкиваясь от гамильтониана Паули-Фирца – он позволяет учесть взаимодействие света с веществом, включая члены A², в дипольном приближении.

На диаграмме слева показаны энергии возбуждений молекулы как функции частоты моды полости ω, при этом цвет точек говорит об их силе осциллятора. Можно видеть формирование светлых поляритонов (красные точки) и набор темных состояний (синие точки). А справа показано сравнение уровней для покоящейся и движущейся молекулы. В целом видно, что энергии возбуждений неслабо модифицируются из-за наличия полости, а их силы осциллятора оказываются зависящими от движения центра масс.

#фотоника #химия

В методе функционала плотности (DFT) есть подстава: точный функционал плотности, определяемый как минимальная внутренняя энергия многоэлектронной системы с заданным профилем плотности n(r), должен иметь изломы в некоторых местах пространства этих функций.

Причина в том, что энергия ионизации I (минимальная энергия, требуемая для удаления электрона из системы) и сродство к электрону A (electron affinity – максимальная энергия, получаемая при добавлении электрона) связаны с производными энергии по дробному числу электронов N при подходе к целому числу Nₒ слева и справа. В изоляторах из-за наличия энергетической щели I > A, как показано на графике черным цветом.

Поэтому функционал должен иметь изломы на гиперповерхностях ∫n(r)dr = Nₒ в пространстве функций n(r), а обменно-корреляционный потенциал должен иметь там разрывы. Понятно, что составленные вручную приближенные функционалы будут гладкими (красные точки на рисунке), и это причина известного провала DFT при предсказании щелей в изоляторах.

#твердое_тело

Самая известная скалярная функция матрицы – это ее определитель. Менее известны перманент и пфаффиан. Перманент матрицы можно, как и определитель, записать в виде суммы произведений матричных элементов по перестановкам строк или столбцов, но без множителя ±1. Он появляется, например, вместо определителя Слэтера при записи симметричной волновой функции системы бозонов. Пфаффиан – это что-то вроде корня определителя для антисимметричной матрицы.

А вот более хитрая штука – торонтониан матрицы, придуманный исследователями из Торонто. Эта функция очень сложна для расчета на классических компьютерах, а вот фотонные квантовые компьютеры считают ее довольно быстро, что было продемонстрировано, например, в этом эксперименте. Фотонный квантовый компьютер, оперирующий 216 оптическими модами, считает торонтониан за 36 микросекунд, в то время как лучшим современным суперкомпьютерам для этого понадобилось бы 9000 лет. Это один из нескольких известных на сегодняшний день примеров квантового превосходства, продемонстрированного на практике квантовыми компьютерами.

Торонтониан возникает при решении следующей задачи: имеем многомодовое гауссово состояние фотонов – то есть состояние с матрицей плотности в виде гауссовой функции <α|ρ|α'> ~ exp(–[α – <α>]S[α'* – <α'*>]/2) в базисе когерентных состояний с некоторой матрицей сжатия S. Нужно найти вероятность того, что это состояние, попав на детекторы, заставит первый детектор обнаружить s₁ фотон, второй – s₂ фотонов и так далее. Вычисление такой совместной вероятности срабатывания детекторов, называемое бозонным сэмплингом, сводится к расчету торонтониана матрицы A, составленной из строк и столбцов исходной ковариационной матрицы S, повторяющихся sᵢ раз для каждой i-й фотонной моды.

На классическом компьютере торонтониан матрицы A может быть вычислен перебором всех 2ᴺ подмножеств Z множества [N] = {1, 2, ..., N}, где N = Σᵢsᵢ – полное число детектируемых фотонов во всех модах. При каждом перебираемом подмножестве Z мы должны составить некую матрицу A(Z) и посчитать определитель det[I – A(Z)]: он, в степени –1/2, войдет в торонтониан с положительным либо отрицательным знаком, в зависимости от четности числа элементов в Z.

Матрица A(Z) составляется из исходной матрицы A взятием строк и столбцов только с теми номерами, которые встречаются в Z. При этом исходные матрицы S и A имеют блочную структуру 2×2, образующуюся из-за разбиения комплексных чисел α = x + ip на вещественные «координату» и «импульс» фотона, и матрицы A(Z) тоже наследуют эту блочную структуру.

Например, в случае N = 3 имеем [N] = {1, 2, 3} и множество всех его подмножеств есть {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}. Величина Z пробегает все эти варианты и в случае Z = {1,2} в матрице A(Z) мы в каждом блоке оставляем только элементы на 1-й и 2-й строках и столбцах и на их пересечениях.

Таким образом, для расчета торонтониана матрицы мы должны перебирать все подмножества ее строк и столбцов, вычисляя для каждого из таких подмножеств определитель, при этом сохраняя блочную структуру матриц. Вычисление торонтониана матрицы (2N×2N) требует O(N³2ᴺ) операций, то есть является экспоненциально трудной задачей.

#квантовые_вычисления #фотоника #объяснения

Пролиферация вихрей и антивихрей выше температуры перехода Березинского-Костерлица-Таулеса (БКТ) приводит к разрушению сверхтекучести: изолированные вихри в сверхтекучем потоке подвергаются силе Магнуса и движутся, ослабляя его с течением времени. А в этой работе предсказано сохранение противотоковой сверхтекучести выше температуры БКТ в двухслойном сверхпроводнике.

Как показано сверху, противотоковая сверхтекучесть заключается в том, что проводимость σ₋(ω) относительно токов, текущих в двух слоях в противоположных направлениях, ведет себя как σ₋(ω) ~ i/ω. Расходимость мнимой части при ω → 0 – это признак отклика идеального проводника. Проводимость же по отношению к симметричным электрическим полям в двух слоях σ₊(ω) ведет себя нормально.

Рисунки снизу показывают, как вихри, образующиеся выше температуры БКТ, оказываются двухслойными, поэтому не подвергаются эффекту Магнуса в противоположных токах – это и есть причина сохранения противотоковой сверхтекучести.

#сверхпроводимость #сверхтекучесть

Знаменитый звук растрескивания (crackling sound), возникающий при разрывании бумаги и, в более крупных масштабах, при землетрясениях – одно из ярких проявлений самоорганизации в критических системах. Такой звук состоит из последовательности лавин – перестроек системы, обладающих масштабно-инвариантной статистикой в широком диапазоне.

Вот эксперимент, в котором листы бумаги растягивали с измерением механического натяжения по мере распространения в них разрыва. Примеры полученных зависимостей показаны точками на графике сверху: они состоят из последовательности щелчков. Статистика энергий, высвобождающихся при каждом таком щелчке, и промежутков времени между ними показаны на нижних графиках – соответственно, слева и справа.

Как видно, энергии E и времена τ встречаются с частотами, подчиняющимися степенным законам 1/E^1.25 и 1/τ. Это масштабно-инвариантные зависимости, простирающиеся на несколько порядков и свидетельствующие о самоорганизованной критичности процесса растрескивания.

#самоорганизация #акустика

Невероятно красивый эксперимент с использованием жидких кристаллов с топологическими дефектами в качестве активной среды для лазерной генерации.

Как показано сверху, внутрь резонатора Фабри-Перо можно поместить, к примеру, каплю жидкого кристалла-нематика с вихрем, вокруг которого молекулы выстраиваются в радиальный узор (и туда же добавить краситель, служащий активной средой). Оптическая анизотропия жидкого кристалла будет приводить к лазерной генерации целого набора мод с хитрыми пространственными и поляризационными картинами – это примеры так называемого структурированного света.

Более того, ориентацией молекул и оптическими свойствами жидкого кристалла можно управлять внешним электрическим полем (что используется в ЖК-мониторах) – а значит, можно менять и структуру генерируемого света. Пример такой перестройки, наблюдавшейся в эксперименте, показан на панелях D-F снизу.

#фотоника #электродинамика

Вот еще пара красивых картинок из статьи про лазерную генерацию в жидкокристаллическом резонаторе.

1) Генерация мод на антивихре в нематике, упорядоченной решетке вихрей и антивихрей, а также неупорядоченной структуре, в которой вихри и антивихри встречаются в случайных местах.

2) Кольцевые моды, генерируемые в жидком кристалле с киральным топологическим дефектом тороидальной формы, называемым тороном.

3) Генерация мод на кончиках «киральных пальцев», образующихся в жидком кристалле-холистерике.

#фотоника #электродинамика

При низких температурах вязкость жидкостей убывает с ростом T, поскольку молекулам становится легче перескакивать между «клетками» из ближайших соседей. При высоких же T она начинает расти с температурой из-за уменьшения времени свободного пробега. Между этими двумя зависимостями вязкость достигает минимума, как показано на графиках для динамической вязкости η и кинематической вязкости ν = η/ρ (ρ – это плотность жидкости).

В этой работе показано, что кинематическая вязкость ν любой жидкости, по порядку величины, не может падать ниже универсального предела ħ/4π√(m_e×m), где m_e – масса электрона, m – масса молекулы. А «элементарная вязкость» i = νm и вовсе ограничена комбинацией фундаментальных констант (ħ/4π)√(m_p/m_e), где m_p – масса протона.

Рассуждения авторов основываются на том, что длина свободного пробега молекул жидкости не может быть меньше их размера порядка боровского радиуса. Похожим образом выводится критерий Иоффе-Регеля для минимальной удельной проводимости материалов.

#гидродинамика

Нулевой уровень Ландау графена в сильном магнитном поле расщепляется на 4 подуровня из-за комбинации эффекта Зеемана и многочастичного спонтанного нарушения симметрии, природа которого не до конца понятна. В качестве возможных сценариев предлагались ферромагнитная и антиферромагнитная фазы, волна зарядовой плотности, искажение Кекуле и т.д. Все эти фазы проявляются похожим образом в виде расщепления уровня Ландау, поэтому для их различения нужно смотреть на более тонкие эффекты.

В этом эксперименте с такой целью анализировалась структура краевых состояний графена в магнитном поле, образованных расщепленным нулевым уровнем Ландау. Показанная снизу картина изгиба подуровней как функция координаты вблизи края образца получена сканирующей кельвиновской силовой микроскопией: этот метод основанный на чувствительности частоты колебаний иглы атомного силового микроскопа к электростатическому потенциалу вблизи образца, позволяет получать карту локального химического потенциала электронов.

#графен #уровни_Ландау

Интересный эксперимент с очередной реализацией неэрмитовой системы с исключительными точками, демонстрирующей невзаимность распространения поверхностных плазмонов.

Здесь на металл наложена диэлектрическая дифракционная решетка, элементарная ячейка которой содержит две разные диэлектрические полоски. Изменение расстояния s между ними позволяет двигаться вдоль контура в пространств параметров, показанного справа зеленым кругом: от одной исключительной точки до зеркально симметричной ей. Поверхностный плазмон при этом, как показано моделированием в центре, постепенно переходит от распространяющегося вправо к распространяющемуся влево. Крайние случаи отвечают PT-симметричным случаям.

Результаты эксперимента, показанные ниже, подтверждают эти ожидания. По мере изменения параметра s мы плавно меняем направление распространения плазмонов, как видно и в координатном, и в импульсном представлениях, и на графике для контраста интенсивности C_exc между левым и правым направлениями.

#неэрмитовы_системы #плазмоны

А вот еще любопытный эффект из статьи из предыдущего поста, где наложенная на металл диэлектрическая дифракционная решетка находится в режиме исключительных точек PT-симметричной неэрмитовой системы.

Невзаимность распространения поверхностных плазмонов в этом режиме делает дифракционную решетку однонаправленным зеркалом для двумерной оптики. А именно, когда плазмон, бегущий по поверхности металла, наталкивается на участок с дифракционной решеткой, он будет отражаться от нее по-разному с разных сторон.

Как показано результатами моделирования на панелях A и C, падающий слева плазмон хорошо отражается, что приводит к формированию ярко выраженной стоячей волны из-за интерференции падающей и отраженных волн (C), а падающий справа плазмон отражается хуже, так что стоячая волна менее выражена (A). Это подтверждается экспериментальными измерениями профиля поля, показанными на панели B.

#неэрмитовы_системы #плазмоны

Небольшой обзор по статистической физике активной материи – систем взаимодействующих частиц, способных к активному движению за счет внешнего либо внутреннего источника энергии. Частицы могут двигаться случайных направлениях либо синхронизировать направление своего движения с ближайшими соседями – как это происходит, например, в стаях птиц или рыб.

Теоретические подходы к изучению активной материи основываются на уравнениях Ланжевена, в которые добавляется активная движущая сила. Затем на основе таких уравнений движения для отдельных частиц строится эффективная теория поля, описывающая эволюцию непрерывных полей плотности и скоростей частиц.

Отличительные особенности активной материи – это способность частиц сбиваться в сгустки (как в случае «живых кристаллов»), а также выстраивать направление своего движения – это называется flocking transition. В некоторых моделях возникают три фазы: неупорядоченный «газ», выстроенная «жидкость» и упорядоченный «кристалл».

#самоорганизация #биология

Незатухающие токи в основном состоянии квантовой системы возможны не только в сверхпроводниках, но и в достаточно малых проводниках. Они чем-то похожи на вращение электрона вокруг ядра в атоме, которое не затухает просто потому, что ему некуда затухнуть – других квантовых состояний с меньшей энергией не существует.

Конечно, все это происходит только во внешнем магнитном поле, нарушающим теорему Блоха и делающим возможными ненулевые токи в основном состоянии. На рисунке показаны примеры магнитного момента круговой квантовой точки (сверху) и тока, циркулирующего по кольцу (снизу) как функций магнитного поля. Можно видеть, как на крупные осцилляции Ааронова-Бома накладываются мелкие осцилляции де Хааза-ван Альфена, показанные в увеличенном виде на графиках справа. Последние обусловлены последовательными переходами уровня Ферми через уровни Ландау.

Авторы посчитали все как для плоской системы, так и в геометрии Лобачевского, где задача об электронах в магнитном поле тоже решается аналитически.

#уровни_Ландау

Интересная статья Марка Мезара – известного специалиста по физике спиновых стекол – с размышлениями о современных проблемах теории стекол и статистической теории обучения.

В спиновых стеклах большое число спинов взаимодействуют друг с другом случайным образом: какие-то пары спинов взаимодействуют ферромагнитно, какие-то – антиферромагнитно. Один и самых серьезных вызовов теории спиновых стекол – в том, как проводить усреднение по реализациям таких неупорядоченных интегралов взаимодействия.

Статистическая теория обучения – исследующая, в частности, процесс обучения нейронных сетей – имеет множество параллелей с теорией спиновых стекол. При рассмотрении динамики конкретной нейросети состояния ее нейронов (активный/неактивный) можно считать аналогом ориентаций спина (вверх/вниз), а параметры сети (веса межнейронных связей и смещения) можно считать аналогом интегралов взаимодействий между спинами.

Но при анализе обучения нейронной сети более полезной оказывается другая параллель: параметры сети, которые меняются в ходе обучения, можно считать аналогом спиновых состояний, а роль беспорядка – интегралов взаимодействия – играют фиксированные данные обучающей выборки. При обучении нейросеть нащупывает оптимальное состояние, подстроенное под конкретную реализацию беспорядка ради уменьшения функции потерь. Подобным образом спиновое стекло при низких температурах оптимизирует свое состояние, уменьшая свободную энергию. Большой вопрос здесь – как нейросеть подстраивается под другие реализации беспорядка (то есть другие обучающие выборки) и проявляются ли в такой подстройке некие универсальные черты ее поведения, называемые способностью к обобщению данных.

#стекла #нейронные_сети

Вот это улетная работа, в которой проведен сравнительный анализ адиабатически медленной эволюции классических и квантовых систем.

Квантовая адиабатическая эволюция происходит при изменениях гамильтониана системы, медленной по сравнению с расстояниями между энергетическими уровнями. В ходе такой эволюции система остается на текущем уровне, но ее волновая функция приобретает – в дополнение к обычной, динамической фазе – еще и геометрическую фазу. Последняя превращается в фазу Берри при обходе замкнутого контура в пространстве параметров гамильтониана.

Классическая адиабатическая эволюция тоже, в принципе, хорошо изучена. Простейшим ее примером является осциллятор с медленно меняющейся частотой собственных колебаний ω(t). У него сохраняется адиабатический инвариант E/ω, и это приводит к тому, что амплитуда колебаний медленно меняется как 1/√ω(t).

Можно ли найти какие-то параллели между настолько различными явлениями? Авторы для этого использовали трюк, популярный, например, в теории акустических топологических изоляторов: если квантовая система обладает гамильтонианом H, то «аналогичная ей» классическая система может быть описана квадрированным гамильтонианом H². Это приводит к важному следствию: если у простейшей двухуровневой квантовой системы есть лишь одна энергия возбуждения ω, то в классической системе будет как положительно-частотный «энергетический уровень» ω, так и отрицательно-частотный партнер –ω (потому что оба собственных значения ±ω исходного гамильтониана H дадут физически неотличимые собственные значения ω² гамильтониана H²).

Если не обращать внимание на это различие, то, в некоторых случаях, адиабатическая эволюция квантовой и классической систем может быть весьма похожа: если энергетические щели между уровнями энергии остаются достаточно большими, то обе системы остаются на своих энергетических уровнях, не перескакивая на другие. В классическом случае «оставаться на своем энергетическом уровне» как раз и означает сохранение классического адиабатического гамильтониана.

Различие кроется в существовании отрицательно-частотных уровней у классической системы. Если какой-либо из ее уровней энергии становится мал по абсолютной величине, то энергетическая щель между уровнями-партнерами ω и –ω становится слишком малой. Как следствие, между ними происходят переходы, что приводит к нарушению адиабатической эволюции классической системы.

Таким образом, в квантовой системе для адиабатической эволюции нужно, чтобы щели между различными энергетическими уровнями ωᵢ были достаточно велики (по сравнению со скоростью изменения гамильтониана). В классической системе, помимо этого условия, требуется также, чтобы и сами энергии уровней ωᵢ находились достаточно далеко от нуля.

Наконец, напишу пару слов о причине такого различия. Эволюция квантовой системы с течением времени описывается нестационарным уравнением Шредингера с гамильтонианом H. Уравнения же Гамильтона для классической системы тоже можно записать в виде некоторого аналога уравнения Шредингера – но с неэрмитовым гамильтонианом! Именно неэрмитова добавка делает возможными переходы между положительно-частотными и отрицательно-частотными уровнями, невозможные в исходной квантовой системе.

#квантовая_механика #механика #отвал_башки

А вот наглядный пример из статьи с сопоставлением классической и квантовой адиабатической эволюции. Авторы рассмотрели двухуровневую квантовую систему и ее классический аналог, который, из-за наличия отрицательно-частотных уровней, обладает 4 состояниями.

На графиках показаны четыре примера модуляции энергии двух уровней с течением времени (красная и синяя кривые) и соответствующего поведения амплитуд заселения энергетических уровней для квантовой (черная и красная кривые) и классической (остальные цвета) систем.

В случае 1 все адиабатично: и щель между уровнями, и сами их энергии велики, так что обе системы остаются в прежних состояниях. Если щель остается большой, но сама энергия нижнего уровня почти достигает нуля (случай 2), то квантовая система ведет себя адиабатично, а классическая – уже нет. В случаях 3 и 4 щель между уровнями временами сильно уменьшается, так что обе системы переходят на с начального уровня на другие – хотя и по-разному в случае 3.

#квантовая_механика #механика #отвал_башки

Встречайте HeLIOS (Helium ultraLIght dark matter Optomechanical Sensor) – детектор для гипотетических сверхлегких частиц темной материи, основанный на сверхтекучем гелии-4. Он представлен герметичным цилиндрическим сосудом с жидким гелием, сверху накрытым тонкой металлической мембраной с выступом в центре. Мембрана служит нижней стенкой небольшого микроволнового резонатора с резонансной частотой, чрезвычайно чувствительной к ее малым вертикальным сдвигам.

Если темная материя состоит из сверхлегких частиц массой меньше 10 эВ, их плотность должна быть достаточно велика для формирования классической волны – подобно классической электромагнитной волне, получающейся при большой плотности фотонов. Волна скалярных частиц может, предположительно, создавать в массе гелия осциллирующие натяжения, возбуждающие «дышащие» моды (с четными индексами на рисунке), а волна векторных частиц – осциллирующую силу, возбуждающую моды с нечетными индексами.

#астрофизика #сверхтекучесть

А вот диаграммы из статьи из предыдущего поста, показывающие возможности нового детектора HeLIOS для частиц темной материи в сравнении с другими существующими детекторами.

Красным цветом показаны диапазоны масс частиц (по горизонтали) и силы их взаимодействия с материей (по вертикали), покрываемые HeLIOS. Две диаграммы отвечают скалярным и векторным частицам, по-разному взаимодействующими с материей: скалярные частицы могут модулировать постоянную тонкой структуры или массу фермионов, а векторные могут раскачивать материю осциллирующей силой.

Благодаря тому, что детектор использует целый набор стоячих мод звуковых колебаний сверхтекучего гелия в сосуде, а их частоты могут перестраиваться изменением давления, удается покрыть довольно широкий диапазон масс.

#астрофизика #сверхтекучесть

Когерентные машины Изинга (или квантово-оптические нейронные сети) способны быстро находить решения экспоненциально трудных оптимизационных задач благодаря комбинации квантовых и нелинейных эффектов. Авторы этой работы откладывают в сторону квантовые эффекты и анализируют, что происходит при этом с самим энергетическим ландшафтом задачи.

Как я писал подробнее в этой статье, в ходе работы когерентной машины Изинга амплитуда лазерной накачки a постепенно увеличивается, и когда она переходит через некоторый порог, коллективное состояние взаимодействующих оптических параметрических осцилляторов оказывается, в идеале, в глобальном минимуме энергии.

Если рассмотреть один осциллятор, то его энергетический ландшафт –ax² + x⁴ ведет себя как при фазовом переходе 2-го рода: при a < 0 у нас имеется единственный минимум x = 0, а при a > 0 происходит бифуркация на два минимума x = ±√a. В случае большого числа связанных осцилляторов происходит что-то похожее, но в многомерном и неупорядоченном варианте: изначально выпуклый вниз ландшафт, имеющий единственный минимум в нуле, при увеличении a постепенно уплощается, и на нем развивается множество локальных минимумов, среди которых постепенно выделяется единственный, ярко выраженный глобальный минимум.

Авторы исследуют эволюцию многомерного ландшафта при помощи метода реплик, теории случайных матриц и аппарата суперсимметрии. По итогам анализа, они выделяют несколько этапов:

1) При a < a_r ландшафт остается выпуклым вниз и имеет единственный минимум в нуле. Соответственно, когерентная машина Изинга как квантовая система остается, на фоне такого ландшафта, в более-менее хорошем вакуумном состоянии.

2) При a_r < a < a_t локальных минимумов становится уже много, но на самом деле их число субэкспоненциально по N – числу осцилляторов, и все они примерно одинаково неглубокие. Это проявление суперсимметрии – симметрии системы по отношению к превращению бозонов в фермионы и обратно – возникающей при анализе задачи методом реплик. Квантовое состояние когерентной машины Изинга при этом должно быть, по идее, сильно флуктуирующим вакуумом.

3) При a_t < a < a_g суперсимметрия нарушается. Это проявляется в том, что число локальных минимумов становится уже экспоненциальным по N, и в пределе N →∞ система приобретает ненулевую сложность (complexity) – энтропию, связанную со способностью застревать в одном из этих минимумов и говорящую о неопределенности коллективного состояния системы. При этом локальные минимумы перестают быть статистически эквивалентными: среди них появляются более мелкие и более глубокие, а самый глубокий из них становится глобальным.

Тем не менее, минимумы остаются маргинально устойчивыми: из каждого из них можно выйти с небольшими затратами энергии. И глобальный минимум тоже не очень-то глубок на фоне остальных. Можно предположить, что квантовое состояние машины при этом все еще сильно флуктуирует, но уже сосредотачивается вблизи глобального минимума – хотя и не макроскопически большой долей своей волновой функции.

4) Наконец, при a > a_g происходит так называемый переход жесткости (rigidity transition): глобальный минимум становится очень глубоким на фоне остальных, а выход из него стоит макроскопически большой энергии. Иными словами, спектр гессиана – то есть собственные значения матрицы вторых производных энергии по координатам ландшафта – в этой точке положителен и отделен от нуля конечной щелью. То есть колебания вблизи этой точки становятся «жесткими». Квантовое состояние машины Изинга при этом уже макроскопически концентрируется в глобальном минимуме.

На самом деле, таких «глобальных минимумов» может быть довольно много, и все они примерно одинаково глубоко и одинаково жесткие. С практической точки зрения, не столь уж важно, в какой из них мы попадем, потому что все они будут давать более-менее одинаково хорошие решения оптимизационной задачи. Еще один практический вывод, который делают авторы, состоит в том, что нет нужды повышать a выше a_g: на этом месте работу когерентной машины Изинга можно уже останавливать.

#стекла #нейронные_сети #оптимизация

А вот иллюстрация из статьи из предыдущего поста, на которой можно видеть признаки описанной там эволюции потенциального ландшафта.

На графике сверху показаны типичные энергии критических точек ландшафта, где производная обращается в ноль. Среди них можно выделить локальные минимумы, а остальные – это либо седловые точки, либо локальные максимумы. Можно видеть, как при переходе накачки a через a_r на ландшафте постепенно развиваются минимумы, причем неглубокие: их энергия, в пределе N →∞, такая же, как у остальных критических точек. При пересечении второго порога a_t минимумы и остальные критические точки разделяются по энергиям, а при a > a_g глобальный минимум особенно сильно углубляется.

Диаграммы снизу иллюстрируют иерархию критических точек при a > a_g: чем дальше они от начала координат, тем ниже по энергии и тем ниже их индекс – число отрицательных собственных значений гессиана, то есть направленных вниз по энергии направлений на ландшафте.

#стекла #нейронные_сети #оптимизация