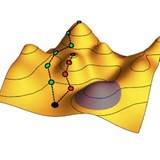
А вот физическое объяснение того, почему горизонтальные (τ_xx, τ_yy) и вертикальная (τ_zz) компоненты тензора напряжений различаются на поверхности жидкости, давая начало поверхностному натяжению.

τ_αβ определяет скорость переноса импульса через площадку ориентации α в направлении β. Он происходит за счет перемещения молекул вместе со своим импульсом (кинетическая часть) и за счет сил межмолекулярного взаимодействия через площадку (потенциальная часть). Как можно показать, кинетические части в горизонтальном и вертикальном направлениях одинаковы, так что нужно сравнить лишь потенциальные вклады.

Как показано снизу, на границе жидкости, в среднем по ее толщине, в горизонтальном направлении взаимодействуют молекулы с плотностями, равными полусумме плотности жидкости ρ_L и пара ρ_V, откуда τ_xx = τ_yy ~ [(ρ_L + ρ_V)/2]². В вертикальном же направлении друг с другом взаимодействуют молекулы с плотностями ρ_L и ρ_V, откуда τ_zz ~ ρ_L×ρ_V. А поскольку [(a+b)/2]² > ab, получаем τ_xx = τ_yy > τ_zz.

#гидродинамика

Свежий обзор по топологическим изоляторам высшего порядка – материалам, обладающим необычными модами внутри щели не на границе, а на ее углах и стыках.

Угловые состояния (corner states), возникающие в двумерном случае, можно интерпретировать следующим образом: граница материала представляет собой одномерный топологический изолятор с различными значениями топологического инварианта при разных ее направлениях. Поэтому на углах образуются доменные стенки, где формируются связанные состояния внутри щели.

Аналогичным образом в трехмерном случае возникают петельные состояния (hinge states): на его поверхности, представляющей собой двумерный топологический изолятор, в местах стыков образуются одномерные доменные стенки.

Топологические изоляторы высшего порядка обладают необычными инвариантами, связанными и квадрупольным и октупольным моментами. Для них изготовлено довольно много электрических аналогов, но и несколько твердотельных реализаций тоже были обнаружены в последние годы.

#топологические_материалы

Формирование угловых состояний в топологическом изоляторе второго порядка можно понять при помощи модели Беналказара-Берневига-Хьюеса (Benalcazar-Bernevig-Hughes model).

Это квадратная решетка с 4 узлами в элементарной ячейке с интегралами перескока γ_x и γ_y по горизонтали и вертикали внутри ячейки и с интегралами перескока λ_x и λ_y между ячейками. Как показано на диаграмме для энергетических уровней, найденных численно для квадратного образца, при |γ_x/ λ_x| < 1 и |γ_y/ λ_y| < 1 внутри щели образуются состояния, которые локализованы вблизи углов.

Аналогично модели Су-Шриффера-Хеегера, их формирование можно понять, отталкиваясь от предельного полностью димеризованного режима γ_x, γ_y = 0. Как показано снизу, в этом случае квантовые состояния в углах оказываются изолированы от остальной решетки. Постепенное увеличение γ_x и γ_y включает перескоки внутри голубых квадратов и слегка делокализует эти состояния, но не меняет качественно их свойства.

#топологические_материалы

Интересно, что угловые и петельные состояния на границах топологических изоляторов высшего порядка были предсказаны не только для кристаллов, но и для структур, не имеющих кристаллического порядка: аморфных материалов, квазикристаллов и даже гиперболической решетке, возникающей в пространстве постоянной отрицательной кривизны.

#топологические_материалы

Любопытный анализ того, могут ли возникать черты классического хаоса в современных квантовых компьютерах, состоящих из большого числа сверхпроводниковых кубитов-трансмонов.

Каждый трансмон можно считать нелинейным математическим маятником, режим работы которого ограничивается основным |0> и первым возбужденным |1> состояниями. Связанные классические нелинейные маятники должны демонстрировать хаотическую динамику. Авторы показывают, что это происходит и в квантовой системе трансмонов, если их достаточно много, а сила их взаимодействия достаточно велика: динамика становится хаотической даже несмотря на работу в существенно квантовом режиме (в пределах состояний |0> и |1>) и даже несмотря на расстройку энергий возбуждений, вносимую во избежание резонансов.

На рисунке показано, когда, по мере увеличения взаимодействия T, существующие и будущие квантовые процессоры IBM пересекают порог показателя Ляпунова λ = 0.04, при котором динамика становится уже заметно хаотической.

#квантовые_вычисления #механика

А вот пример того, как черты классического хаоса возникают в системе взаимодейстсвующих кубитов-трансмонов.

Десять кубитов, связанных друг с другом с силой T, инициализируются в состоянии |1010…>. При этом энергии возбуждения кубитов случайно распределены с дисперсией δE_J. На панели (а) точкам отвечают все базисные многокубитные состояния |i>, а их размеры показывает их вклады <i|ψ(t)> в волновую функцию системы |ψ(t)> в разные моменты времени. На панели (b) показан обратный коэффициент участия (inverse participation ratio) Σᵢ|<i|ψ(t)>| ⁴, который велик при локализации состояния в небольшом числе векторов |i> и мал при ее делокализаци по большому числу разных |i>.

Когда T мало по сравнению с δE_J (синий цвет), динамика системы регулярна: волновая функция остается, в значительной мере, сосредоточена вблизи начального состояния |1010…>. При сильном же взаимодействии (желтый цвет) система быстро размешивается по гильбертову пространству, что говорит о хаотической динамике.

#квантовые_вычисления #механика

Относительно недавняя, но уже высокоцитируемая статья, хорошо продвинувшая теорию неэрмитовых твердотельных систем. В ней была разработана так называемая неблоховская теория, дающая рецепт обобщения зонной теории твердых тел на неэрмитовы системы.

Проблема таких систем в том, что непонятно даже, что в них брать в качестве квазиимпульса k. Должен ли он быть вещественным или комплексным? А если комплексным, то каким именно? И что для него играет роль первой зоны Бриллюэна?

В одномерном случае неблоховская теория строится на рассмотрении вместо квазиимпульса k комплексного числа β = exp(ik). Уравнение для комплексных энергий E бесконечной цепочки det[H(β) – E] = 0 имеет вид полиномиального уравнения некоторой четной степени 2M относительно параметра β. Действительно, в случае модели Хатано-Нельсона – цепочки с различными перескоками вправо t и влево t´ между ближайшими соседями – гамильтониан H(β) имеет матричные элементы tβ и t´β⁻¹, так что для энергии мы получаем формулу E = –(tβ + t´β⁻¹) вместо обычного выражения E(k) = –2t cos(k) в эрмитовом случае t = t´. Как видно, при известной E у нас получается квадратное уравнение относительно параметра β, то есть 2M = 2. При более сложных перескоках или большем числе узлов в одной элементарной ячейке степень уравнения 2M будет выше.

Дальше рецепт следующий: при каждой комплексной энергии E мы находим 2M корней уравнения дисперсии, которые упорядочиваем по возрастанию модуля |β₁| ≤ |β₂| ≤ … Среди всех возможных E мы выбираем лишь такие, при которых |β_M| = |β_{M+1}|, то есть два корня в самой середине этой цепочки совпадают по модулю. Именно такой набор энергий даст нам непрерывную зонную структуру неэрмитового кристалла, а сами значения β_M либо β_{M+1} дадут одномерную замкнутую кривую на комплексной плоскости β, являющуюся неэрмитовым аналогом первой зоны Бриллюэна. В эрмитовом случае все βᵢ имеют единичный модуль, так что указанное выше условие тривиально выполняется, а первая зона Бриллюэна имеет вид единичного круга |β| = 1.

Я не особо понял объяснения авторов насчет того, чем должно быть обусловлено условие |β_M| = |β_{M+1}|: они сводятся к тому, что среди M корней βᵢ, максимальных по модулю, должно быть два совпадающих по абсолютной величине, что дает возможность плавно варьировать относительную фазу значений волновой функции на соседних узлах и получать непрерывные, хоть и комплексные, энергетические зоны. В противном случае все развалится на дискретные уровни, не имеющие физического смысла.

Интересно, что процедура построения неблоховской теории, как утверждается, не зависит от вида граничных условий где-то далеко на концах цепочки, поскольку она имеет дело лишь с асимптотическим поведением волновых функций в глубине ее толщи. А в случае более высокой размерности решетки нужно вводить несколько параметров βᵧ = exp(ikᵧ) вдоль разных координатных осей, но общий рецепт остается прежним.

#неэрмитовы_системы #твердое_тело #объяснения

А вот пример из статьи из предыдущего поста, иллюстрирующий возникновение неэрмитового аналога первой зоны Бриллюэна.

Здесь рассматривается неэрмитова модель Су-Шриффера-Хеегера. Как видно, у нее есть целая куча комплексных интегралов перескока, а уравнение дисперсии имеет 2M = 4 корня. Синие кривые показывают траектории параметра β = exp(ik) на комплексной плоскости, возникающие при выполнении условия |β₂| = |β₃| построения непрерывных энергетических зон для разных значений параметров системы. Это и есть неэрмитовы первые зоны Бриллюэна. Как видно, это замкнутые кривые, на которых β может быть по модулю как больше, так и меньше 1 – это означает и комплексность квазиимпульса k.

Диаграммы снизу показывают спектры комплексных энергий – то есть энергетические зоны, найденные численно для ограниченной цепочки (слева) и аналитически из неблоховской теории (справа). Как видно, картины совпадают, и мы действительно получаем сплошные зоны – значит, модель работает.

#неэрмитовы_системы #твердое_тело #объяснения

В курсе физики твердого тела учат игрушечным моделям для электронов в кристалле – например, модели почти свободных электронов. На практике же для расчета электронных свойств реальных веществ используются другие методы. Эта книга 2006 года дает хорошее представление о стандартных моделях, используемых для описания основных свойств твердых тел, молекул и жидкостей.

Основные модели – в принципе, не сильно изменившиеся с года выхода книги – включают в себя:
• Метод функционала плотности для основного состояния кристалла или молекулы.
• Метод функционала плотности с возмущением атомных позиций для описания фононов и электрон-фононного взаимодействия.
• Метод GW, уравнение Бете-Солпитера и нестационарный метод функционала плотности для описания оптических спектров.
• Первопринципную молекулярную динамику для молекулярных систем.
• Аппарат функций Ванье для описания квантовой электростатики материалов.
• Формулу Кубо, уравнение Больцмана и теорию Ландауэра для описания электрической проводимости.

#твердое_тело

Любопытный эксперимент, в котором взаимодействие между атомами бозе-сконденсированного облака периодически модулировали за счет резонанса Фешбаха, из-за чего в нем стала спонтанно формироваться квадратная решетка.

Пример показан на рисунке: на диаграммах сверху изображены профили атомного облака в разные моменты времени в координатном пространстве, на диаграммах снизу – в импульсном. Как видно, сначала облако довольно хаотично (панель (a)), затем в нем начинают возникать модуляции плотности с волновыми векторами определенного модуля, но случайными направлениями (b).

После 21 периода модуляции выживают лишь две взаимно перпендикулярные модуляции плотности (c). Правые диаграммы на панели (c) показывают картины, усредненные по множеству запусков эксперимента: как видно, ориентация этих модуляций каждый раз случайна. Наконец, при дальнейших модуляциях система заполняется возбуждениями со всевозможными другими импульсами, так что квадратная решетка разрушается.

#бозе_конденсация #атомные_газы #самоорганизация

Красивый эксперимент с переносом энтропии в изолированной квантовой системе в условиях сверхтекучести.

Облако атомов-фермионов ⁶Li, находящееся в сверхтекучем состоянии в унитарном режиме, разделяется на две части, соединенные тонкой перемычкой. Авторы создавали между двумя частями создается управляемый дисбаланс температуры и числа, а затем наблюдали, как этот дисбаланс выравнивается посредством перетекания атомов через перемычку. На графиках точки разного цвета показывают, как, при разных ширинах перемычки, выравнивается дисбаланс числа частиц (a) и энтропии (b). Система в целом является изолированной, что подтверждается постоянством полной энтропии (c).

А необычно здесь то, что энтропия, переносимая каждой частицей, почти постоянна и равна примерно s* = 1.18, что подтверждается зависимостями ΔS = ΔNs* на панели (d). Эта величина гораздо выше, чем предсказывается двухжидкостной гидродинамикой с нормальной и сверхтекучей компонентами.

#атомные_газы #сверхтекучесть #термодинамика

Хороший, появившийся буквально вчера, обзор по фотоэлектронной спектроскопии с угловым и временным разрешением (time-resolved angle-resolved photoemission spectroscopy, TR-ARPES). Этот метод стремительно развивается в последние годы в связи с появлением новых, более интенсивных и качественных источников излучения фотонов высокой энергии, и активно используется для исследования квантовых материалов – топологических изоляторов, двумерных кристаллов, сильно-коррелированных систем и т.д.

В этом методе образец сначала накачивается лазерным импульсом, из-за чего электроны заполняют возбужденные состояния, а затем, после управляемой задержки, подвергается фотоэлектронной спектроскопии, дающей информацию о квазиимпульсах и энергиях этих заполненных состояний. Так можно не только определять ветви электронной дисперсии, находящиеся выше уровня Ферми, но и анализировать динамику возбужденных состояний, а также изучать более тонкие эффекты типа процессов формирования экситонов.

#твердое_тело

В режиме сверхсильной связи света с веществом в основном состоянии системы не только имеется какое-то ненулевое количество фотонов, но эти фотоны находятся еще и в сжатом состоянии. А в этой работе реализован режим многомодовой сверхсильной связи, при котором расщепление Раби превышает разность частот двух или большего числа электромагнитных мод.

Достигнуто это в системе двух трехмерных фотонных кристаллов, между которыми зажат двумерный электронный газ в сильном магнитном поле. Оптические переходы между уровнями Ландау связывают между собой две TM-поляризованные и две TE-поляризованные электромагнитные моды. Я не особо понял объяснения авторов, но S-образная дисперсия поляритона, виднеющаяся на панели (B) снизу для случая TE-мод, каким-то образом подтверждает существование многомодового режима сверхсильной связи. А графики справа показывают расчетные числа фотонов каждой моды и перекрестный член между ними, отличные от нуля в основном состоянии системы.

#фотоника #поляритоны #уровни_Ландау

Загадочная структура из статьи из предыдущего поста, выглядящая, как кадр из советского диафильма.

#цитаты

В системе с взаимодействием света с веществом, существует ultrastrong coupling regime, который я всегда переводил как режим сверхсильной связи. А еще бывает, оказывается, superstrong coupling regime – и как его теперь переводить? Режим супер-пупер-сильной связи?

#фотоника #цитаты

Интересная работа с реализацией демона Максвелла на основе металлического наноостровка, соединенного туннельными переходами с двумя контактами.

Принцип его работы следующий: когда электрон находится на островке (состояние 2 на рисунке), демон делает его потенциал положительным, чтобы пытаться максимально удержать электрон. Если же островок пуст (состояние 4), демон делает его потенциал отрицательным, чтобы отталкивать электроны и не дать его заселить. Таким образом, процессы перехода электрона между островком и контактами (зеленые стрелки) всегда совершают положительную работу, независимо от их направления.

Самое интересное, что описанная обратная связь – изменения потенциала островка – осуществляется не вручную, а сама собой, за счет эффекта кулоновской блокады. Получается автономно работающий демон Максвелла, охлаждающий контакты (синие и зеленые точки на графиках), но нагревающий островок (красные точки), потому что демону приходится стирать свою память, выделяя тепло.

#стохастическая_термодинамика

Эксперимент с наблюдением исключительных точек в неэрмитовой системе – метаповерхности, на которой возбуждаются плазмонные моды.

Метаповерхность состоит из двух массивов металлических кирпичиков, сдвинутых по горизонтали. Как показано сверху (Configuration 1), в такой структуре происходит гибридизация плазмонных мод с пересечением их энергий и расщеплением скоростей затухания. Если же нарушить симметрию системы (Configuration 3), поместив один из массивов внутрь диэлектрика, а другой снаружи, то система становится неэрмитовой: в ней, на диаграммах зависимостей энергии и скорости потерь от двух параметров системы, появляется исключительная точка.

При проходе мимо этой точки с двух разных сторон (белые и черные кривые) наблюдаются контрастные картины: с одной стороны мы видим антипересечение энергий и пересечение скоростей затухания, с другой стороны – наоборот, пересечение энергий и антипересечение затуханий. Экспериментальные точки, показанные снизу, это подтверждают.

#неэрмитовы_системы #плазмоны

А вот еще один эксперимент с наблюдением исключительных точек – на этот раз, в экситон-плазмонной системе.

Плазмоны образуются на поверхности серебряной подложки, где вырезан массив наноканавок. Интервал между канавками медленно меняется вдоль образца, так что исследование разных его участков дает возможность медленно менять частоту плазмона, плавно проходя через исключительную точку. Второй компонент системы – это слой двумерного WS₂, лежащего на подложке сверху, экситоны которого гибридизуются с плазмонами.

Получается двухуровневая неэрмитова система с исключительной точкой, в которой один энергетический уровень расщепляется на два, расходящихся как квадратный корень расстройки между частотами экситона и плазмона. Экспериментальные графики подтверждают такое поведение спектральных линий.

Корневая зависимость, производная которой расходится в точке бифуркации, делают систему очень чувствительной к изменениям параметров – этим исключительные точки интересны на практике.

#неэрмитовы_системы #плазмоны

В последние годы становятся популярными исследования химических реакций в оптической полости: оказывается, квантование электромагнитных мод в ограниченной геометрии заметно модифицирует свойства молекул и влияет на ход некоторых химических реакций.

В этой работе рассмотрен пример такой модификации. Авторы численно решили уравнение Шредингера для молекулы HD⁺, состоящей из трех частиц, отталкиваясь от гамильтониана Паули-Фирца – он позволяет учесть взаимодействие света с веществом, включая члены A², в дипольном приближении.

На диаграмме слева показаны энергии возбуждений молекулы как функции частоты моды полости ω, при этом цвет точек говорит об их силе осциллятора. Можно видеть формирование светлых поляритонов (красные точки) и набор темных состояний (синие точки). А справа показано сравнение уровней для покоящейся и движущейся молекулы. В целом видно, что энергии возбуждений неслабо модифицируются из-за наличия полости, а их силы осциллятора оказываются зависящими от движения центра масс.

#фотоника #химия

В методе функционала плотности (DFT) есть подстава: точный функционал плотности, определяемый как минимальная внутренняя энергия многоэлектронной системы с заданным профилем плотности n(r), должен иметь изломы в некоторых местах пространства этих функций.

Причина в том, что энергия ионизации I (минимальная энергия, требуемая для удаления электрона из системы) и сродство к электрону A (electron affinity – максимальная энергия, получаемая при добавлении электрона) связаны с производными энергии по дробному числу электронов N при подходе к целому числу Nₒ слева и справа. В изоляторах из-за наличия энергетической щели I > A, как показано на графике черным цветом.

Поэтому функционал должен иметь изломы на гиперповерхностях ∫n(r)dr = Nₒ в пространстве функций n(r), а обменно-корреляционный потенциал должен иметь там разрывы. Понятно, что составленные вручную приближенные функционалы будут гладкими (красные точки на рисунке), и это причина известного провала DFT при предсказании щелей в изоляторах.

#твердое_тело

Самая известная скалярная функция матрицы – это ее определитель. Менее известны перманент и пфаффиан. Перманент матрицы можно, как и определитель, записать в виде суммы произведений матричных элементов по перестановкам строк или столбцов, но без множителя ±1. Он появляется, например, вместо определителя Слэтера при записи симметричной волновой функции системы бозонов. Пфаффиан – это что-то вроде корня определителя для антисимметричной матрицы.

А вот более хитрая штука – торонтониан матрицы, придуманный исследователями из Торонто. Эта функция очень сложна для расчета на классических компьютерах, а вот фотонные квантовые компьютеры считают ее довольно быстро, что было продемонстрировано, например, в этом эксперименте. Фотонный квантовый компьютер, оперирующий 216 оптическими модами, считает торонтониан за 36 микросекунд, в то время как лучшим современным суперкомпьютерам для этого понадобилось бы 9000 лет. Это один из нескольких известных на сегодняшний день примеров квантового превосходства, продемонстрированного на практике квантовыми компьютерами.

Торонтониан возникает при решении следующей задачи: имеем многомодовое гауссово состояние фотонов – то есть состояние с матрицей плотности в виде гауссовой функции <α|ρ|α'> ~ exp(–[α – <α>]S[α'* – <α'*>]/2) в базисе когерентных состояний с некоторой матрицей сжатия S. Нужно найти вероятность того, что это состояние, попав на детекторы, заставит первый детектор обнаружить s₁ фотон, второй – s₂ фотонов и так далее. Вычисление такой совместной вероятности срабатывания детекторов, называемое бозонным сэмплингом, сводится к расчету торонтониана матрицы A, составленной из строк и столбцов исходной ковариационной матрицы S, повторяющихся sᵢ раз для каждой i-й фотонной моды.

На классическом компьютере торонтониан матрицы A может быть вычислен перебором всех 2ᴺ подмножеств Z множества [N] = {1, 2, ..., N}, где N = Σᵢsᵢ – полное число детектируемых фотонов во всех модах. При каждом перебираемом подмножестве Z мы должны составить некую матрицу A(Z) и посчитать определитель det[I – A(Z)]: он, в степени –1/2, войдет в торонтониан с положительным либо отрицательным знаком, в зависимости от четности числа элементов в Z.

Матрица A(Z) составляется из исходной матрицы A взятием строк и столбцов только с теми номерами, которые встречаются в Z. При этом исходные матрицы S и A имеют блочную структуру 2×2, образующуюся из-за разбиения комплексных чисел α = x + ip на вещественные «координату» и «импульс» фотона, и матрицы A(Z) тоже наследуют эту блочную структуру.

Например, в случае N = 3 имеем [N] = {1, 2, 3} и множество всех его подмножеств есть {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}. Величина Z пробегает все эти варианты и в случае Z = {1,2} в матрице A(Z) мы в каждом блоке оставляем только элементы на 1-й и 2-й строках и столбцах и на их пересечениях.

Таким образом, для расчета торонтониана матрицы мы должны перебирать все подмножества ее строк и столбцов, вычисляя для каждого из таких подмножеств определитель, при этом сохраняя блочную структуру матриц. Вычисление торонтониана матрицы (2N×2N) требует O(N³2ᴺ) операций, то есть является экспоненциально трудной задачей.

#квантовые_вычисления #фотоника #объяснения