Как известно, атеизм – это тоже религия, а некурящие – тоже курульщики, которые курят отсутствие табака. Вот и авторы этой статьи тоже считают, что отсутствие механического воздействия (перемешивания, встряхивания и т.д.) на сосуд с раствором – это тоже один из режимов механического воздействия.

#цитаты #химия

Отталкивание (антипересечение) энергетических уровней при гибридизации состояний – одно из базовых явлений квантовой механики. А в этом эксперименте наблюдалось противоположное явление притяжения (или схлопывания) уровней.

Оно возникает за счет эффекта Ленца – диссипативного взаимодействия микроволн в резонаторе с магнитным моментом шарика, схожего с явлением магнитного торможения. При таком взаимодействии изменение магнитного момента шарика создает индукционные токи в металлических стенках резонатора, стремящиеся заглушить изменение магнитного потока.

Эффект Ленца создает чисто мнимое расщепление Раби между магнонной модой шарика и электромагнитной модой резонатора. Как следствие, при достаточном сближении их частот вместо двух вещественных собственных значений гамильтониана двухуровневой системы мы получаем два комплексно сопряженных корня. Общая вещественная часть обоих корней дает картину двух «схлопнувшихся» энергетических уровней, которая и наблюдалась в эксперименте.

#квантовая_механика #магнетизм

В этом эксперименте показано, что экситонный поляритон в оптической микрополости за счет диссипации может иметь отрицательную массу.

Теоретически, диссипация учитывается добавлением к гамильтониану мнимого слагаемого, действующего по-разному на фотоны и экситоны и смешивающего их между собой. В отличие от расщепления Раби, которое приводит к отталкиванию дисперсий фотона и экситона, общий канал их затухания (например, превращение в фонон) приводит к притяжению дисперсий. Это похоже на явление притяжения энергетических уровней, описанное в предыдущем посте.

Комбинация отталкивания и притяжения дает перевернутую дисперсию нижнего поляритона, наблюдаемую в эксперименте с микрополостью, содержащей слой оксида кремния. На ней есть участок с отрицательной групповой скоростью. Как показано снизу, это проявляется в заселении нижними поляритонами состояний с импульсами k, противоположными по направлению поляритонному потоку (при этом верхние поляритоны заселяют k-состояния, сонаправленные потоку).

#поляритоны

В предыдущем посте я писал об эксперименте, продемонстрировавшем появление отрицательной групповой скорости и отрицательной массы у экситонных поляритонов в оптической полости за счет диссипации. В этой работе утверждается, что подобное явление должно быть довольно распространенным в физике поляритонов.

Авторы рассмотрели эванесцентные моды – или поверхностные поляритоны, – распространяющиеся вдоль двумерного проводящего слоя, обладающего резонансным откликом и диссипацией. На графиках сверху показаны примеры вещественных и мнимых частей дисперсий поляритонов TM- (синие кривые ) и TE-поляризаций (красные кривые). Если увеличить часть левой картинки для TM-моды в области внутри светового конуса, мы увидим дисперсию с отрицательной групповой скоростью.

Аналитическая формула для приближенно квадратичной дисперсии такой моды показывает, что за счет диссипации γ_D к ней добавляется отрицательный вклад, который, в определенном диапазоне параметров системы, может пересиливать положительный.

#поляритоны #плазмоны

При обтекании примеси электрическим током вокруг нее образуется электрический диполь – анизотропное пространственное распределение электронной плотности, – направленный вдоль или против тока. Один из механизмов его образования, показанный на рисунке слева (RRD) и уже наблюдавшийся в экспериментах – это рассеяние, из-за которого отраженные от примеси электроны дают сгущение отрицательного заряда сзади. В этом случае направление диполя не зависит от заряда примеси.

В этой работе впервые наблюдался другой механизм (CDM, показанный справа): примесь положительного заряда создает вблизи себя сгущение электронов, которое сносится потоком и создает диполь, направленный параллельно току. Для отрицательно заряженной примеси все наоборот.

Сверхчувствительные измерения пространственных профилей потенциала вблизи двухслойного графена методом сканирующей туннельной потенциометрии показывают (снизу на рисунке), как направление таких диполей зависят от направления тока и знака заряда примесей.

#твердое_тело #графен

А вот кроссовер физики неэрмитовых систем и физики связанных состояний в континууме – работа, в которой теоретически предсказано существование исключительных точек для связанных состояний в континууме при внесении в систему потерь, делающих ее динамику неэрмитовой.

Связанные состояния в континууме возникают в массиве диэлектрических дисков, составляющих фотонный кристалл, или метаповерхность. Как показано слева, при сближении двух метаповерхностей образуются расщепленные по энергии симметричные и антисимметричные комбинации таких состояний.

Если же, как показано справа, в одну из метаповерхностей внести потери (например, проделав небольшие отверстия в дисках, заставляющие излучение утекать), на зависимостях энергий мод от расстояния между поверхностями появляется исключительная точка. При этом скорости затухания (верхний график) также демонстрируют бифуркацию: одна из расщепленных мод приобретает большие потери, другая – гораздо меньшие.

#электродинамика #неэрмитовы_системы

Формула Стреды (Středa formula) – это известная формула, связывающая удельную холловскую проводимость в режиме квантового эффекта Холла – при нулевой диагональной проводимости – с откликом электронной плотности n на магнитное поле B. Здесь считается, что химический потенциал электронов постоянен, так что при увеличении B новые электроны могут перетекать в проводник из внешнего резервуара, увеличивая n.

В оригинальной работе она была получена из квантовомеханически, но ее можно получить и из классических соображений. Представим, что мы увеличиваем B в некоторой области образца (площадью S и с периметром L), тогда из-за электромагнитной индукции вокруг нее возникает вихревое электрическое поле E. За счет холловской проводимости, это поле создает перпендикулярные полю электрические токи j, вытекающие из области и меняющие ее заряд Q, а значит, и электронную плотность n внутри области.

#твердое_тело #уровни_Ландау #объяснения

Кстати говоря, еще одна интерпретация формулы Стреды такая: если, при фиксированном положении уровня Ферми, мы увеличиваем магнитное поле B, то увеличивается и пропорциональная ему кратность вырождения каждого уровня Ландау g = eSB/πħc (она умножена на 2 для учета электронного спина).

Если уровень Ферми все время находится внутри щели между N-м и (N+1)-м уровнями Ландау, то удельная холловская проводимость квантуется как σ_xy = 2e²N/h (тоже с учетом спина), где h = 2πħ. Поскольку заполнены ровно N уровней Ландау, полная электронная плотность равна n = Ng/S = NeB/πħc, откуда ec(∂n/∂B) = σ_xy.

В общем, если смотреть с физической точки зрения, то: сильнее магнитное поле → выше кратность вырождения каждого уровня Ландау → больше суммарное число электронов на всех заполненных уровнях Ландау → выше электронная плотность.

#твердое_тело #уровни_Ландау #объяснения

Любопытная теоретическая статья, связывающая между собой такие фундаментальные вещи, как число Черна, формулу Стреды и теорему Латинджера.

Формула Стреды (см. два поста выше) дает нам удельную холловскую проводимость, пропорциональную числу Черна C двумерного топологического изолятора. Выражая электронную плотность n через функцию Грина G и проводя манипуляции с функциями Грина и собственно-энергетическими частями, авторы представляют C в виде двух слагаемых.

Первое из них N₃[G] – это третья группа гомотопии для функций Грина, возникающая как топологический инвариант в теории многочастичных топологических изоляторов. Второе слагаемое ΔN₃[G], как показывают авторы, отлично от нуля только при нарушении теоремы Латинджера, то есть в сильно-коррелированных системах.

Таким образом, авторам удалось соотнести друг с другом два по-разному определяемых топологических инварианта и доказать, что они равны в «нормальных» системах, где выполняется теорема Латинджера.

#топологические_материалы #уровни_Ландау

Вот это бомбическая статья, переворачивающая с ног на голову традиционные представления о переобучении нейросетей.

В практике работы с нейросетями хорошо известна кривая обучения, показанная на рисунке сверху: по мере увеличения способностей нейросети к фитированию функций H (например, числа ее параметров) сначала мы находимся в режиме недообучения (underfitting), когда и тренировочная, и тестовая ошибки высоки, а затем переходим в режим переобучения (overfitting), при котором нейросеть идеально фитирует обучающую выборку сильно извилистой функцией, из-за чего тестовая ошибка начинает расти.

Однако современные нейросети имеют настолько большие H, что должны находиться далеко в режиме переобучения. Почему же они хорошо работают? Дело в том, что при дальнейшем росте H, как показано снизу, тестовая ошибка снова начинает падать, потому что нейросеть начинает фитировать данные уже более гладкими функциями, поскольку они проще и предпочтительнее из-за регуляризации.

#нейронные_сети #популярное #отвал_башки

А вот пара примеров из статьи о переобучении нейросетей.

Слева и справа показано, как тренировочная и тестовая ошибки ведут себя как функции числа параметров системы при обучении плотной нейросети и, соответственно, модели случайного леса распознаванию изображений из базы MNIST при двух разных вариантах функции ошибок.

Как видно, вместо традиционной U-образной кривой для тестовой ошибки получаются кривые с падением ошибки при достаточно больших числах параметров машинной модели. Можно сказать, что достаточно мощные нейросети реализуют принцип Оккама: из всех возможных фитирующих функций они выбирают самые простые (самые гладкие), избегая переобучения. А старые представления о компромиссе между отклонением и дисперсией (bias-variance tradeoff) для них неприменимы.

Занятно, что открытое явление раньше ускользало от внимания исследователей – скорее всего, потому что работа велась либо целиком в левой, либо целиком в правой части кривых, далеко от разделяющего их пика.

#нейронные_сети #популярное #отвал_башки

Как нас обычно учат, поверхностное натяжение возникает из-за того, что находиться на поверхности жидкости молекулам энергетически менее выгодно, чем в ее толще: во втором случае они имеют больше партнеров для притягивающего взаимодействия.

Однако не все так просто: например, как показано на рисунке слева, в такой наивной картине молекулы на поверхности должны суммарно втягиваться внутрь, а не стягиваться по горизонтали. Как объясняется в этом педагогическом введении, коэффициент поверхностного натяжения γ можно выразить через интеграл по вертикальной координате z от разности между горизонтальной (τ_xx + τ_yy)/2 и вертикальной τ_zz компонентами тензора напряжений в жидкости. Эта связь называется уравнением Бэккера (Bakker’s equation).

На рисунке справа показаны зависимости плотности вещества ρ и компонент тензора напряжений τ, посчитанные методом молекулярной динамики. Как видно, на границе между жидкостью и паром, где ρ быстро спадает, τ_xx и τ_yy действительно заметно отличаются от τ_zz.

#гидродинамика

А вот физическое объяснение того, почему горизонтальные (τ_xx, τ_yy) и вертикальная (τ_zz) компоненты тензора напряжений различаются на поверхности жидкости, давая начало поверхностному натяжению.

τ_αβ определяет скорость переноса импульса через площадку ориентации α в направлении β. Он происходит за счет перемещения молекул вместе со своим импульсом (кинетическая часть) и за счет сил межмолекулярного взаимодействия через площадку (потенциальная часть). Как можно показать, кинетические части в горизонтальном и вертикальном направлениях одинаковы, так что нужно сравнить лишь потенциальные вклады.

Как показано снизу, на границе жидкости, в среднем по ее толщине, в горизонтальном направлении взаимодействуют молекулы с плотностями, равными полусумме плотности жидкости ρ_L и пара ρ_V, откуда τ_xx = τ_yy ~ [(ρ_L + ρ_V)/2]². В вертикальном же направлении друг с другом взаимодействуют молекулы с плотностями ρ_L и ρ_V, откуда τ_zz ~ ρ_L×ρ_V. А поскольку [(a+b)/2]² > ab, получаем τ_xx = τ_yy > τ_zz.

#гидродинамика

Свежий обзор по топологическим изоляторам высшего порядка – материалам, обладающим необычными модами внутри щели не на границе, а на ее углах и стыках.

Угловые состояния (corner states), возникающие в двумерном случае, можно интерпретировать следующим образом: граница материала представляет собой одномерный топологический изолятор с различными значениями топологического инварианта при разных ее направлениях. Поэтому на углах образуются доменные стенки, где формируются связанные состояния внутри щели.

Аналогичным образом в трехмерном случае возникают петельные состояния (hinge states): на его поверхности, представляющей собой двумерный топологический изолятор, в местах стыков образуются одномерные доменные стенки.

Топологические изоляторы высшего порядка обладают необычными инвариантами, связанными и квадрупольным и октупольным моментами. Для них изготовлено довольно много электрических аналогов, но и несколько твердотельных реализаций тоже были обнаружены в последние годы.

#топологические_материалы

Формирование угловых состояний в топологическом изоляторе второго порядка можно понять при помощи модели Беналказара-Берневига-Хьюеса (Benalcazar-Bernevig-Hughes model).

Это квадратная решетка с 4 узлами в элементарной ячейке с интегралами перескока γ_x и γ_y по горизонтали и вертикали внутри ячейки и с интегралами перескока λ_x и λ_y между ячейками. Как показано на диаграмме для энергетических уровней, найденных численно для квадратного образца, при |γ_x/ λ_x| < 1 и |γ_y/ λ_y| < 1 внутри щели образуются состояния, которые локализованы вблизи углов.

Аналогично модели Су-Шриффера-Хеегера, их формирование можно понять, отталкиваясь от предельного полностью димеризованного режима γ_x, γ_y = 0. Как показано снизу, в этом случае квантовые состояния в углах оказываются изолированы от остальной решетки. Постепенное увеличение γ_x и γ_y включает перескоки внутри голубых квадратов и слегка делокализует эти состояния, но не меняет качественно их свойства.

#топологические_материалы

Интересно, что угловые и петельные состояния на границах топологических изоляторов высшего порядка были предсказаны не только для кристаллов, но и для структур, не имеющих кристаллического порядка: аморфных материалов, квазикристаллов и даже гиперболической решетке, возникающей в пространстве постоянной отрицательной кривизны.

#топологические_материалы

Любопытный анализ того, могут ли возникать черты классического хаоса в современных квантовых компьютерах, состоящих из большого числа сверхпроводниковых кубитов-трансмонов.

Каждый трансмон можно считать нелинейным математическим маятником, режим работы которого ограничивается основным |0> и первым возбужденным |1> состояниями. Связанные классические нелинейные маятники должны демонстрировать хаотическую динамику. Авторы показывают, что это происходит и в квантовой системе трансмонов, если их достаточно много, а сила их взаимодействия достаточно велика: динамика становится хаотической даже несмотря на работу в существенно квантовом режиме (в пределах состояний |0> и |1>) и даже несмотря на расстройку энергий возбуждений, вносимую во избежание резонансов.

На рисунке показано, когда, по мере увеличения взаимодействия T, существующие и будущие квантовые процессоры IBM пересекают порог показателя Ляпунова λ = 0.04, при котором динамика становится уже заметно хаотической.

#квантовые_вычисления #механика

А вот пример того, как черты классического хаоса возникают в системе взаимодейстсвующих кубитов-трансмонов.

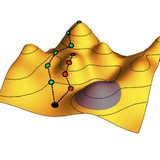
Десять кубитов, связанных друг с другом с силой T, инициализируются в состоянии |1010…>. При этом энергии возбуждения кубитов случайно распределены с дисперсией δE_J. На панели (а) точкам отвечают все базисные многокубитные состояния |i>, а их размеры показывает их вклады <i|ψ(t)> в волновую функцию системы |ψ(t)> в разные моменты времени. На панели (b) показан обратный коэффициент участия (inverse participation ratio) Σᵢ|<i|ψ(t)>| ⁴, который велик при локализации состояния в небольшом числе векторов |i> и мал при ее делокализаци по большому числу разных |i>.

Когда T мало по сравнению с δE_J (синий цвет), динамика системы регулярна: волновая функция остается, в значительной мере, сосредоточена вблизи начального состояния |1010…>. При сильном же взаимодействии (желтый цвет) система быстро размешивается по гильбертову пространству, что говорит о хаотической динамике.

#квантовые_вычисления #механика

Относительно недавняя, но уже высокоцитируемая статья, хорошо продвинувшая теорию неэрмитовых твердотельных систем. В ней была разработана так называемая неблоховская теория, дающая рецепт обобщения зонной теории твердых тел на неэрмитовы системы.

Проблема таких систем в том, что непонятно даже, что в них брать в качестве квазиимпульса k. Должен ли он быть вещественным или комплексным? А если комплексным, то каким именно? И что для него играет роль первой зоны Бриллюэна?

В одномерном случае неблоховская теория строится на рассмотрении вместо квазиимпульса k комплексного числа β = exp(ik). Уравнение для комплексных энергий E бесконечной цепочки det[H(β) – E] = 0 имеет вид полиномиального уравнения некоторой четной степени 2M относительно параметра β. Действительно, в случае модели Хатано-Нельсона – цепочки с различными перескоками вправо t и влево t´ между ближайшими соседями – гамильтониан H(β) имеет матричные элементы tβ и t´β⁻¹, так что для энергии мы получаем формулу E = –(tβ + t´β⁻¹) вместо обычного выражения E(k) = –2t cos(k) в эрмитовом случае t = t´. Как видно, при известной E у нас получается квадратное уравнение относительно параметра β, то есть 2M = 2. При более сложных перескоках или большем числе узлов в одной элементарной ячейке степень уравнения 2M будет выше.

Дальше рецепт следующий: при каждой комплексной энергии E мы находим 2M корней уравнения дисперсии, которые упорядочиваем по возрастанию модуля |β₁| ≤ |β₂| ≤ … Среди всех возможных E мы выбираем лишь такие, при которых |β_M| = |β_{M+1}|, то есть два корня в самой середине этой цепочки совпадают по модулю. Именно такой набор энергий даст нам непрерывную зонную структуру неэрмитового кристалла, а сами значения β_M либо β_{M+1} дадут одномерную замкнутую кривую на комплексной плоскости β, являющуюся неэрмитовым аналогом первой зоны Бриллюэна. В эрмитовом случае все βᵢ имеют единичный модуль, так что указанное выше условие тривиально выполняется, а первая зона Бриллюэна имеет вид единичного круга |β| = 1.

Я не особо понял объяснения авторов насчет того, чем должно быть обусловлено условие |β_M| = |β_{M+1}|: они сводятся к тому, что среди M корней βᵢ, максимальных по модулю, должно быть два совпадающих по абсолютной величине, что дает возможность плавно варьировать относительную фазу значений волновой функции на соседних узлах и получать непрерывные, хоть и комплексные, энергетические зоны. В противном случае все развалится на дискретные уровни, не имеющие физического смысла.

Интересно, что процедура построения неблоховской теории, как утверждается, не зависит от вида граничных условий где-то далеко на концах цепочки, поскольку она имеет дело лишь с асимптотическим поведением волновых функций в глубине ее толщи. А в случае более высокой размерности решетки нужно вводить несколько параметров βᵧ = exp(ikᵧ) вдоль разных координатных осей, но общий рецепт остается прежним.

#неэрмитовы_системы #твердое_тело #объяснения

А вот пример из статьи из предыдущего поста, иллюстрирующий возникновение неэрмитового аналога первой зоны Бриллюэна.

Здесь рассматривается неэрмитова модель Су-Шриффера-Хеегера. Как видно, у нее есть целая куча комплексных интегралов перескока, а уравнение дисперсии имеет 2M = 4 корня. Синие кривые показывают траектории параметра β = exp(ik) на комплексной плоскости, возникающие при выполнении условия |β₂| = |β₃| построения непрерывных энергетических зон для разных значений параметров системы. Это и есть неэрмитовы первые зоны Бриллюэна. Как видно, это замкнутые кривые, на которых β может быть по модулю как больше, так и меньше 1 – это означает и комплексность квазиимпульса k.

Диаграммы снизу показывают спектры комплексных энергий – то есть энергетические зоны, найденные численно для ограниченной цепочки (слева) и аналитически из неблоховской теории (справа). Как видно, картины совпадают, и мы действительно получаем сплошные зоны – значит, модель работает.

#неэрмитовы_системы #твердое_тело #объяснения

В курсе физики твердого тела учат игрушечным моделям для электронов в кристалле – например, модели почти свободных электронов. На практике же для расчета электронных свойств реальных веществ используются другие методы. Эта книга 2006 года дает хорошее представление о стандартных моделях, используемых для описания основных свойств твердых тел, молекул и жидкостей.

Основные модели – в принципе, не сильно изменившиеся с года выхода книги – включают в себя:
• Метод функционала плотности для основного состояния кристалла или молекулы.
• Метод функционала плотности с возмущением атомных позиций для описания фононов и электрон-фононного взаимодействия.
• Метод GW, уравнение Бете-Солпитера и нестационарный метод функционала плотности для описания оптических спектров.
• Первопринципную молекулярную динамику для молекулярных систем.
• Аппарат функций Ванье для описания квантовой электростатики материалов.
• Формулу Кубо, уравнение Больцмана и теорию Ландауэра для описания электрической проводимости.

#твердое_тело