Книга 2018 года почти на 1000 страниц о квантовой термодинамике – точнее, не книга, а сборник статей разных авторов.

В принципе, книга содержит много полезного: основные понятия и формулы, описывающие работу квантовых тепловых машин, различные сценарии получения для них квантового преимущества, применение к ним теории открытых квантовых систем. Отдельная глава с несколькими статьями посвящена роли квантовой информации в термодинамических процессах. А в последней главе собрано описание нескольких недавних экспериментальных реализаций квантовых тепловых машин и квантовых демонов Максвелла.

Конечно, сложно представить, что кто-то будет действительно читать эти 1000 страниц с формулами, но даже прочтение 1-2 статей оттуда может быть довольно просвещающим занятием.

#квантовая_термодинамика

Фишеровская информация (Fisher information) – величина, часто встречающаяся в современных работах по статистике, термодинамике и квантовой информации.

Представим себе какое-нибудь статистическое распределение p(x, θ) случайной величины x, зависящее от параметра θ. Расхождение Кульбака-Лейблера показывает (см. формулу на рисунке), насколько два распределения при двух значениях θ различимы – сколько бит информации требуется для определения, с каким из них мы имеем дело. Для двух близких распределений она квадратична по малому приращению параметра Δθ, а коэффициент пропорциональности – это и есть фишеровская информация. Она говорит о том, насколько быстро, в статистическом смысле, меняется распределение p(x, θ) при изменении θ.

Смысл этой величине придает и знаменитое неравенство Крамера-Рао: оно говорит о том, что любая процедура получения оценки (θ с крышечкой) параметра θ по статистике p(x, θ) будет давать квадрат ошибки, то есть дисперсию, равную обратной фишеровской информации.

#информация #математика

Вот это чумовая работа: теоретический вывод и экспериментальная визуализация потоков фишеровской информации о любых параметрах – расположении, ориентации, диэлектрических свойствах и т.д. – объектов, получаемой при их облучении электромагнитными волнами.

Как радиолокация, так и наше зрение основываются на том, что объекты облучаются электромагнитной волной, а затем рассеянные или отраженные волны детектируются, и по их свойствам мы пытаемся сделать выводы о каких-то параметрах θ объектов (например, угле поворота, как показано на рисунке). Фишеровская информация (см. предыдущий пост) говорит о точности, с которыми мы можем определить эти параметры, детектируя рассеянные волны.

Авторы вводят, по аналогии с вектором Пойнтинга (потоком энергии на панели (а)), плотность потока информации (b), уравнение непрерывности для нее и выражения для плотности источников информации, генерируемой объектами с диэлектрической проницаемостью ε(r, θ) или поглощаемой ими при Im ε > 0.

#электродинамика #информация #отвал_башки

Вот красивый пример генерации фишеровской информации о горизонтальной координате θ диэлектрического слоя в одномерной геометрии рассеяния.

На диэлектрик слева падает волновой пакет, и на верхних графиках (а) показано, как ведет себя в разные моменты плотность электромагнитной энергии. Мы видим частичное прохождение электромагнитного импульса и частичное его отражение от обеих границ раздела.

Для сравнения, на нижних графиках (b) показано поведение плотности фишеровской информации. Пока импульс не добрался до диэлектрика, она равна нулю. Ее генерация начинается при столкновении импульса с диэлектриком на обеих границах раздела (фиолетовых линиях) – потому что именно их горизонтальные координаты здесь важны.

Примечательно, что плотность информации не идет вправо, интерферируя деструктивно, поскольку амплитуда и фаза прошедшего импульса не зависят от горизонтальной координаты θ диэлектрического слоя. Только отраженный сигнал несет информацию о ней.

#электродинамика #информация #отвал_башки

А вот пример измеренных в эксперименте потоков фишеровской информации, переносимых микроволнами, которыми облучают объект с последующим детектированием отраженных сигналов.

Как показано на панели (a), изучаемый объект – это металлический куб, помещенный в плоский волновод, заполненный дополнительно рассеивающими тефлоновыми цилиндрами. Облучение и детектирование каждый раз оптимизировались для максимизации информации, получаемой либо о горизонтальной (θ = x), либо о вертикальной (θ = y) координатах куба.

Потоки информации в пространстве, восстановленные по измеренному распределению поля, показаны на панелях (b)-(c). Можно видеть, как они распространяются к детектору из мест своей генерации – точек, в которых условия распространения волн наиболее сильно меняются при малых вариациях θ. В случае θ = x это обращенная к источнику и детектору боковая поверхность куба, в случае θ = x – его верхняя и нижняя поверхности.

#электродинамика #информация #отвал_башки

Модель Раби описывает взаимодействие кубита с одной модой электромагнитного поля посредством вращающих и противовращающих членов. Выбрасывая последние, ее часто упрощают до модели Джейнса-Каммингса, обладающей интегралом движения С – полным числом возбуждений. Благодаря наличию этого интеграла, модель Джейнса-Каммингса легко решается аналитически.

В случае модели Раби полное число возбуждений не сохраняется, но зато сохраняется его четность, поскольку противовращающие члены изменяют C на ±2. Оказывается, даже такого интеграла движения – четности C – достаточно для точного аналитического решения модели Раби, которое было впервые найдено в этой работе 2011 года.

Уровни энергии системы положительной и отрицательной четности даются нулями функций G₊(x) и G₋(x), построение которых описано на рисунке. На графике показано, как энергии уровней зависят от константы взаимодействия g. В точках пересечений двух уровней G₊(x) и G₋(x) формально не имеют корней – это особые, исключительные случаи.

#фотоника

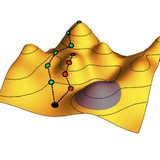
Короткими путями к адиабатичности называют протоколы, позволяющие быстро изменить квантовое состояние системы внешними воздействиями без ее возбуждения. В классической термодинамике такое невозможно: к примеру, при быстром или сжатии или расширении газа в сосуде часть работы неизбежно перейдет в тепло.

В этой работе показано, как быстро расширить одномерный квантовый газ, помещенный между жесткими стенками. Для этого, одновременно с расширением стенок по определенному закону ξ(t), нужно действовать на него квадратичным потенциалом Ω²(t)x²/2, помогающим в нужные моменты разгонять или замедлять частицы. Если правильно подобрать зависимости ξ(t) и Ω²(t), можно добиться сжатия газа (желтые кривые) или его расширения (синие и зеленые кривые) без возбуждения.

Диаграммы снизу показывают, как ведет себя плотность энергии при правильном протоколе расширения (слева) и при обычном линейном по времени сдвиге стенки (справа). Во втором случае в газе образуется множество возбуждений.

#квантовая_термодинамика

Кстати, на этих графиках из предыдущего поста наглядно видно, как работают короткие пути к адиабатичности (shortcuts to adiabaticity).

Если мы хотим сжать газ в сосуде, координата его правой стенки ξ(t) сдвигается слева, как показано желтой кривой на верхнем графике. При этом дополнительный квадратичный потенциал Ω²(t)x²/2, действующий на частицы газа, сначала ускоряет их внутрь, к началу координат (Ω² > 0), а затем отталкивает их обратно, чтобы замедлить (Ω² < 0). Получается протокол, аккуратно ускоряющий и замедляющий частицы во избежание генерации возбуждений над основным состоянием газа.

При расширении сосуда (синяя и зеленая кривые) все наоборот: квадратичный потенциал сначала отталкивает частицы подальше от начала координат, где находится левая стенка (Ω² < 0), а под конец становится удерживающим (Ω² > 0), чтобы замедлить их разлет.

#квантовая_термодинамика

Занятная работа с теоретическим предсказанием жидкого топологического изолятора. Это аморфный топологический изолятор, беспорядок в котором не зафиксирован, а динамически меняется и обусловлен тепловым движением его собственных частиц при температурах выше точки плавления решетки.

Автор рассмотрел двумерную модель сильной связи с двумя орбиталями (s и p + ip) на каждом атоме, а сами атомы движутся под действием как сил со стороны электронной подсистемы, так и собственного отталкивания. Как видно на рисунке сверху, при высокой температуре образуется жидкость (a) с плавно осциллирующей парной корреляционной функцией (c), а при низкой температуре – кристалл с треугольной решеткой (b), (d).

Диаграммы снизу показывают щель в спектре (слева) и индекс Ботта ν, заменяющий для неупорядоченной системы индекс Черна (справа), как функции плотности ρ и температуры T. При ρ > 0.2 ненулевая щель в спектре и топологическая нетривиальность (ν = 1) сохраняются даже при высоких температурах.

#топологические_материалы

Любопытный эксперимент с размножением молекул и их «естественным отбором» под влиянием механических воздействий.

Как показано слева, мономеры – бензольные кольца с присоединенными к ним цепочками аминокислот и тиольными группами (SH) – могут соединяться в кольца различного размера (тримеры, тетрамеры, пентамеры, гексамеры, гептамеры и т.д.). Достаточно длинные кольца (гексамеры и гептамеры) могут, в свою очередь, складываться в стопки, формируя нити диаметром около 5 нм, видимые в электронный микроскоп.

По аналогии с биохимическими процессами, составляющими основу жизни, этот процесс автокаталитический: уже образовавшиеся молекулярные комплексы служат катализатором возникновения новых комплексов. Как показано на графиках справа для распределения размеров циклов, получившегося из раствора мономеров спустя 15-20 дней, результаты зависят от условий, в которых они растут и размножаются. Получается, что механическое воздействие служит для молекул внешним фактором отбора.

#самоорганизация #химия

Как известно, атеизм – это тоже религия, а некурящие – тоже курульщики, которые курят отсутствие табака. Вот и авторы этой статьи тоже считают, что отсутствие механического воздействия (перемешивания, встряхивания и т.д.) на сосуд с раствором – это тоже один из режимов механического воздействия.

#цитаты #химия

Отталкивание (антипересечение) энергетических уровней при гибридизации состояний – одно из базовых явлений квантовой механики. А в этом эксперименте наблюдалось противоположное явление притяжения (или схлопывания) уровней.

Оно возникает за счет эффекта Ленца – диссипативного взаимодействия микроволн в резонаторе с магнитным моментом шарика, схожего с явлением магнитного торможения. При таком взаимодействии изменение магнитного момента шарика создает индукционные токи в металлических стенках резонатора, стремящиеся заглушить изменение магнитного потока.

Эффект Ленца создает чисто мнимое расщепление Раби между магнонной модой шарика и электромагнитной модой резонатора. Как следствие, при достаточном сближении их частот вместо двух вещественных собственных значений гамильтониана двухуровневой системы мы получаем два комплексно сопряженных корня. Общая вещественная часть обоих корней дает картину двух «схлопнувшихся» энергетических уровней, которая и наблюдалась в эксперименте.

#квантовая_механика #магнетизм

В этом эксперименте показано, что экситонный поляритон в оптической микрополости за счет диссипации может иметь отрицательную массу.

Теоретически, диссипация учитывается добавлением к гамильтониану мнимого слагаемого, действующего по-разному на фотоны и экситоны и смешивающего их между собой. В отличие от расщепления Раби, которое приводит к отталкиванию дисперсий фотона и экситона, общий канал их затухания (например, превращение в фонон) приводит к притяжению дисперсий. Это похоже на явление притяжения энергетических уровней, описанное в предыдущем посте.

Комбинация отталкивания и притяжения дает перевернутую дисперсию нижнего поляритона, наблюдаемую в эксперименте с микрополостью, содержащей слой оксида кремния. На ней есть участок с отрицательной групповой скоростью. Как показано снизу, это проявляется в заселении нижними поляритонами состояний с импульсами k, противоположными по направлению поляритонному потоку (при этом верхние поляритоны заселяют k-состояния, сонаправленные потоку).

#поляритоны

В предыдущем посте я писал об эксперименте, продемонстрировавшем появление отрицательной групповой скорости и отрицательной массы у экситонных поляритонов в оптической полости за счет диссипации. В этой работе утверждается, что подобное явление должно быть довольно распространенным в физике поляритонов.

Авторы рассмотрели эванесцентные моды – или поверхностные поляритоны, – распространяющиеся вдоль двумерного проводящего слоя, обладающего резонансным откликом и диссипацией. На графиках сверху показаны примеры вещественных и мнимых частей дисперсий поляритонов TM- (синие кривые ) и TE-поляризаций (красные кривые). Если увеличить часть левой картинки для TM-моды в области внутри светового конуса, мы увидим дисперсию с отрицательной групповой скоростью.

Аналитическая формула для приближенно квадратичной дисперсии такой моды показывает, что за счет диссипации γ_D к ней добавляется отрицательный вклад, который, в определенном диапазоне параметров системы, может пересиливать положительный.

#поляритоны #плазмоны

При обтекании примеси электрическим током вокруг нее образуется электрический диполь – анизотропное пространственное распределение электронной плотности, – направленный вдоль или против тока. Один из механизмов его образования, показанный на рисунке слева (RRD) и уже наблюдавшийся в экспериментах – это рассеяние, из-за которого отраженные от примеси электроны дают сгущение отрицательного заряда сзади. В этом случае направление диполя не зависит от заряда примеси.

В этой работе впервые наблюдался другой механизм (CDM, показанный справа): примесь положительного заряда создает вблизи себя сгущение электронов, которое сносится потоком и создает диполь, направленный параллельно току. Для отрицательно заряженной примеси все наоборот.

Сверхчувствительные измерения пространственных профилей потенциала вблизи двухслойного графена методом сканирующей туннельной потенциометрии показывают (снизу на рисунке), как направление таких диполей зависят от направления тока и знака заряда примесей.

#твердое_тело #графен

А вот кроссовер физики неэрмитовых систем и физики связанных состояний в континууме – работа, в которой теоретически предсказано существование исключительных точек для связанных состояний в континууме при внесении в систему потерь, делающих ее динамику неэрмитовой.

Связанные состояния в континууме возникают в массиве диэлектрических дисков, составляющих фотонный кристалл, или метаповерхность. Как показано слева, при сближении двух метаповерхностей образуются расщепленные по энергии симметричные и антисимметричные комбинации таких состояний.

Если же, как показано справа, в одну из метаповерхностей внести потери (например, проделав небольшие отверстия в дисках, заставляющие излучение утекать), на зависимостях энергий мод от расстояния между поверхностями появляется исключительная точка. При этом скорости затухания (верхний график) также демонстрируют бифуркацию: одна из расщепленных мод приобретает большие потери, другая – гораздо меньшие.

#электродинамика #неэрмитовы_системы

Формула Стреды (Středa formula) – это известная формула, связывающая удельную холловскую проводимость в режиме квантового эффекта Холла – при нулевой диагональной проводимости – с откликом электронной плотности n на магнитное поле B. Здесь считается, что химический потенциал электронов постоянен, так что при увеличении B новые электроны могут перетекать в проводник из внешнего резервуара, увеличивая n.

В оригинальной работе она была получена из квантовомеханически, но ее можно получить и из классических соображений. Представим, что мы увеличиваем B в некоторой области образца (площадью S и с периметром L), тогда из-за электромагнитной индукции вокруг нее возникает вихревое электрическое поле E. За счет холловской проводимости, это поле создает перпендикулярные полю электрические токи j, вытекающие из области и меняющие ее заряд Q, а значит, и электронную плотность n внутри области.

#твердое_тело #уровни_Ландау #объяснения

Кстати говоря, еще одна интерпретация формулы Стреды такая: если, при фиксированном положении уровня Ферми, мы увеличиваем магнитное поле B, то увеличивается и пропорциональная ему кратность вырождения каждого уровня Ландау g = eSB/πħc (она умножена на 2 для учета электронного спина).

Если уровень Ферми все время находится внутри щели между N-м и (N+1)-м уровнями Ландау, то удельная холловская проводимость квантуется как σ_xy = 2e²N/h (тоже с учетом спина), где h = 2πħ. Поскольку заполнены ровно N уровней Ландау, полная электронная плотность равна n = Ng/S = NeB/πħc, откуда ec(∂n/∂B) = σ_xy.

В общем, если смотреть с физической точки зрения, то: сильнее магнитное поле → выше кратность вырождения каждого уровня Ландау → больше суммарное число электронов на всех заполненных уровнях Ландау → выше электронная плотность.

#твердое_тело #уровни_Ландау #объяснения

Любопытная теоретическая статья, связывающая между собой такие фундаментальные вещи, как число Черна, формулу Стреды и теорему Латинджера.

Формула Стреды (см. два поста выше) дает нам удельную холловскую проводимость, пропорциональную числу Черна C двумерного топологического изолятора. Выражая электронную плотность n через функцию Грина G и проводя манипуляции с функциями Грина и собственно-энергетическими частями, авторы представляют C в виде двух слагаемых.

Первое из них N₃[G] – это третья группа гомотопии для функций Грина, возникающая как топологический инвариант в теории многочастичных топологических изоляторов. Второе слагаемое ΔN₃[G], как показывают авторы, отлично от нуля только при нарушении теоремы Латинджера, то есть в сильно-коррелированных системах.

Таким образом, авторам удалось соотнести друг с другом два по-разному определяемых топологических инварианта и доказать, что они равны в «нормальных» системах, где выполняется теорема Латинджера.

#топологические_материалы #уровни_Ландау

Вот это бомбическая статья, переворачивающая с ног на голову традиционные представления о переобучении нейросетей.

В практике работы с нейросетями хорошо известна кривая обучения, показанная на рисунке сверху: по мере увеличения способностей нейросети к фитированию функций H (например, числа ее параметров) сначала мы находимся в режиме недообучения (underfitting), когда и тренировочная, и тестовая ошибки высоки, а затем переходим в режим переобучения (overfitting), при котором нейросеть идеально фитирует обучающую выборку сильно извилистой функцией, из-за чего тестовая ошибка начинает расти.

Однако современные нейросети имеют настолько большие H, что должны находиться далеко в режиме переобучения. Почему же они хорошо работают? Дело в том, что при дальнейшем росте H, как показано снизу, тестовая ошибка снова начинает падать, потому что нейросеть начинает фитировать данные уже более гладкими функциями, поскольку они проще и предпочтительнее из-за регуляризации.

#нейронные_сети #популярное #отвал_башки

А вот пара примеров из статьи о переобучении нейросетей.

Слева и справа показано, как тренировочная и тестовая ошибки ведут себя как функции числа параметров системы при обучении плотной нейросети и, соответственно, модели случайного леса распознаванию изображений из базы MNIST при двух разных вариантах функции ошибок.

Как видно, вместо традиционной U-образной кривой для тестовой ошибки получаются кривые с падением ошибки при достаточно больших числах параметров машинной модели. Можно сказать, что достаточно мощные нейросети реализуют принцип Оккама: из всех возможных фитирующих функций они выбирают самые простые (самые гладкие), избегая переобучения. А старые представления о компромиссе между отклонением и дисперсией (bias-variance tradeoff) для них неприменимы.

Занятно, что открытое явление раньше ускользало от внимания исследователей – скорее всего, потому что работа велась либо целиком в левой, либо целиком в правой части кривых, далеко от разделяющего их пика.

#нейронные_сети #популярное #отвал_башки