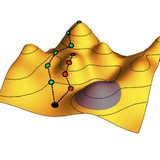
Когерентные машины Изинга – это относительно недавно изобретенные квантово-оптические устройства, которые также называют квантовыми нейронными сетями. Их основа – цепочка лазерных импульсов, бегающих по кругу в длинном оптоволокне и подвергающихся оптической накачке благодаря параметрическому рассеянию. Связывая лазерные импульсы между собой оптическими или оптоэлектронными способами, можно моделировать систему взаимодействующих спинов.

Ряд экспериментов показал, что когерентные машины Изинга способны быстро решать оптимизационные задачи, находя основное состояние системы взаимодействующих спинов и успешно конкурируя в этом плане с машинами D-Wave для квантового отжига – а то и превосходя их. Однако, как и в случае машин для квантового отжига, исследователи еще не до конца понимают, каковы пределы возможностей когерентных машин Изинга и в какой мере они используют квантовое превосходство.

В этой статье я постарался максимально понятно объяснить принцип работы когерентных машин Изинга, не вдаваясь в излишние техническое детали:
https://telegra.ph/Kogerentnye-mashiny-Izinga-kvantovye-nejronnye-seti-bystro-reshayushchie-zadachi-optimizacii-09-03

#оптимизация #фотоника #нейронные_сети #квантовые_вычисления

Как я вижу, авторы этой 100-страничной статьи большие мастера каламбуров: параметр порядка при фазовых переходах 2-го рода у них меняется резко, но плавно, а потом они дают обзор обзора.

#цитаты

Небольшая современная (2021 года) книга по введению в квантовые вычисления.

Автор начинает с самых основ: спина 1/2 и кубитов, сферы Блоха, однокубитных и многокубитных гейтов, ларморовской прецессии и осцилляций Раби. После этого разъясняются главные квантовые алгоритмы: алгоритмы Дойча, Гровера и Шора, квантовая телепортация, квантовое распределение ключей и коррекция ошибок.

Излагается все довольно понятно, компактно и без лишних технических деталей. Отдельно полезны главы о неравенствах Белла и о физических реализациях кубитов. Книга совсем базовая: в ней практически не затрагиваются ни теория вычислительной сложности, ни квантовая информация, ни декогеренция, и в ней вообще не упоминается матрица плотности – все изложение идет лишь на уровне волновых функций.

Тем не менее, книга будет полезна тем, кто хочет разобраться в самых основах квантовых вычислений, причем на современном уровне и с современной терминологией.

#квантовые_вычисления

Что будет, если пытаться максимально отдалить наступление глобальной катастрофы, каждый раз ограничиваясь мелкими, локальными мерами, направленными на самый опасный участок системы?

Как говорит наука о сложных системах, катастрофа действительно наступит заметно позже (чем в отсутствие каких-либо попыток ее предотвратить), но будет иметь гораздо более резкий, «взрывной» характер. В этой 100-страничной статье дается обстоятельный обзор подобных явлений, изучаемых в науке о сложных системах. Самые изученные из них – это взрывная перколяция и взрывная синхронизация.

Примеры перколяции – это распространение эпидемий (вовлечение в процесс заражения заметной доли людей при превышении контагиозностью вируса некоторого порога), лесных пожаров (масштабное распространение огня, охватывающее заметную часть деревьев), формирование социальных связей, распространение вглядов и слухов, глобализация экономики и т.д.

Взрывная перколяция возникает при попытках максимально отдалить точку перколяции, то есть образования связного бесконечного кластера при последовательном добавлении парных связей между узлами случайного или упорядоченного графа. Она была открыта при изучении процессов Ахлиоптаса, подразумевающих на каждом шаге выбор из двух вариантов. Применительно к перколяции это означает, что на каждом шаге мы не просто добавляем случайную связь между узлами, а нам дается возможность выбрать из двух случайных вариантов связи, и мы выбираем тот вариант, при котором образование бесконечного кластера максимально отдаляется. Например, мы из двух предлагаемых связей мы выбираем ту, которая соединит между собой кластеры с наименьшим произведением размеров. В этом случае порог перколяции отдаляется, но наступает она гораздо резче, чем при обычном, случайном добавлении связи. А именно, бесконечный кластер, который при этом образуется, сразу оказывается гораздо большим по размеру.

Взрывная синхронизация возникает при рассмотрении осцилляторов, нелинейно взаимодействующих между собой в духе модели Курамото. Это модель, описывающая систему осцилляторов с некоторым разбросом частот, которые взаимодействуют через силы ~sin(φᵤ(t) – φᵥ(t)), то есть существенно нелинейно. Если сила взаимодействия оказывается достаточно велика по сравнению с разбросом частот, все осцилляторы (или заметная их доля) синхронизуются, то есть начинают колебаться с одинаковой частотой. Если мы пытаемся отдалить этот момент, возникает взрывная синхронизация – более позднее, но более резкое возникновение фазы с заметной долей синхронно колеблющихся осцилляторов. Делать это можно, например, уводя подальше от средней частоты собственные частоты осцилляторов, наиболее сильно взаимодействующих с остальными.

Вот еще несколько интересных моментов из статьи:

● Взрывная перколяция иногда включает в себя образование так называемой «пороховой бочки» – большого числа кластеров, размеры которых еще сублинейны (~ln N либо ~Nᵝ, где β < 1) по сравнению с общим числом узлов N, но которых очень много. Рано или поздно, связи начинают образовываться и между ними, так что они очень быстро объединяются в бесконечный кластер – пороховая бочка взрывается.

● Естественный пример взрывной перколяции – это так называемая diffusion limited aggregation: слипание между собой частиц, совершающих броуновское движение. Самые крупные частицы, образовавшиеся в результате слипания множества мелких, являются самыми «опасными» в плане перколяции, то есть глобального слипания всего в один большой комок. Но они же, за счет своей массивности, совершают броуновское движение медленнее всех остальных, так что природа автоматически пытается максимально устранить их из участия в процессе дальнейшего слипания.

● Знание о том, как максимально отдалить порог перколяции, может быть использовано и для обратной цели: для того, чтобы максимально быстро разобрать уже имеющийся бесконечный кластер. Сюда же можно включить процесс взрывной иммунизации – максимально быстрое устранение эпидемии путем вакцинации людей, имеющих наибольшее число контактов с другими людьми.

#самоорганизация #популярное

Вот простой пример взрывной перколяции на случайном графе.

При классической перколяции мы на каждом шаге добавляем связь между случайной парой узлов. Когда отношение t числа связей к общему числу узлов N превышает пороговое значение, относительный размер самого крупного кластера становится ненулевым в пределе N → ∞, как показано черными точками. Как показано на рисунке снизу для перколяции на квадратной решетки, на пороге перколяции кластеры весьма разнообразны по размерам, а их пространственная структура фрактальна.

Можно пытаться отдалить порог перколяции, пользуясь правилом произведения: нам на выбор даются два случайных варианта связей, и мы выбираем ту, у которой минимально произведение размеров тех кластеров, которые она соединит (например, выбираем связь e₂, а не e₁). В этом случае, как показано красными точками, порог перколяции заметно повышается, но происходит она куда более резко. А распределение размеров кластеров на пороге перколяции становится более равномерным.

#самоорганизация #популярное

А вот пример взрывной синхронизации из этой же статьи.

Обычная синхронизация описывается моделью Курамото: N осцилляторов с различными собственными частотами, которые все друг с другом одинаково нелинейно взаимодействуют с силой K. Параметр порядка r(t) = (1/N)|Σᵢexp(iφᵢ(t))| стремится к 1 при синхронных колебаниях и к 0 в полном отсутствии синхронности. Как видно на панели (a), при переходе K через порог осцилляторы синхронизуются, а панель (b) показывает, как фактические средние частоты их колебаний схлопываются в одну общую, несмотря на различие собственных частот.

Можно попытаться нарушить этот процесс: осцилляторы соединены друг с другом как узлы случайного графа, и мы делаем собственную частоту каждого из них пропорциональной его числу его связей с соседями. Так наиболее перспективные для синхронизации осцилляторы уводятся подальше от общей частоты. Как видно на панелях (c)-(d), синхронизация наступает позже и резче, а еще образуется гистерезис с областью бистабильности.

#самоорганизация #популярное

Краевые магнитоплазмоны – это электромагнитные моды, распространяющиеся вдоль границы двумерного проводника в магнитном поле за счет комбинации циклотронного движения электронов по окружности и их кулоновского взаимодействия между собой.

Аналоги таких мод имеются и на границах квантовых аномальных холловских изоляторов, где реальное магнитное поле отсутствуют, но электроны все равно движутся по окружности из-за кривизны Берри, обусловленной нарушением T-симметрии. Вот пример эксперимента с наблюдением краевых магнитоплазмонов в пленке теллурида висмута и сурьмы, допированной хромом. Из-за последнего в пленке устанавливаются ферромагнетизм и квантовый аномальный эффект Холла.

На диаграммах снизу показаны два примера спектров невзаимного распространения сигналов по круговому образцу против часовой стрелки, на которых видны моды 1-го и 2-го порядков. Дисперсия магнитоплазмонов, собранная с образцов различных диаметров, согласуется с предсказаниями теории.

#уровни_Ландау #плазмоны #топологические_материалы

Сейчас делается много попыток проводить квантово-химические расчеты на квантовых компьютерах, используя их квантовое превосходство в приготовлении классически трудных волновых функций. Авторы этого анализа задаются вопросом: а есть ли вообще экспоненциальное преимущество у имеющихся сегодня квантовых алгоритмов? Оказывается, что нет.

Дело в том, что для работы квантового алгоритма важно, чтобы приготовленное им квантовое состояние хорошо перекрывалось с основным состоянием моделируемой системы. Как показано на панели (C) сверху, для хорошего перекрытия, близкого к 1, время приготовления состояния должно степенным образом расти с числом частиц N.

С другой стороны, для хороших классических алгоритмов (например, метода связанных кластеров) трудоемкость также ~Nᵝ, как видно на панелях (A) и (B) снизу. Получается, что и квантовые, и классические методы, достигающие сравнимой точности, полиномиальны по N, так что на практике ни у кого нет экспоненциального преимущества перед другими.

#квантовые_вычисления #химия

Грамматика Ребера (Reber grammar) – это простая модель генерации последовательностей символов, используемая для тестирования компьютерных моделей, работающих с текстовой информацией.

Для генерации нужно переходить от одного узла к другому по стрелочкам, как указано на рисунке, каждый раз добавляя к текстовой строке соответствующий символ. В случае развилки мы с вероятностью 50% идем по одному из путей (в том числе, когда развилка «внутренняя», то есть один из вариантов – остаться на месте, как указано круговой стрелкой).

К примеру, после начального символа B мы можем добавить T или P, после T – S или X, и так далее. У грамматики Ребера есть свои правила: например, S может идти после T, но только если до символа T стоял символ B. Есть и менее очевидные правила. Машинные модели – например, нейронные сети, – можно тестировать на предмет умения распознавать, является ли строка реберовой (удовлетворяющей правилам грамматики) или не-реберовой (нарушающей правила).

#популярное #нейронные_сети

Книга 2018 года почти на 1000 страниц о квантовой термодинамике – точнее, не книга, а сборник статей разных авторов.

В принципе, книга содержит много полезного: основные понятия и формулы, описывающие работу квантовых тепловых машин, различные сценарии получения для них квантового преимущества, применение к ним теории открытых квантовых систем. Отдельная глава с несколькими статьями посвящена роли квантовой информации в термодинамических процессах. А в последней главе собрано описание нескольких недавних экспериментальных реализаций квантовых тепловых машин и квантовых демонов Максвелла.

Конечно, сложно представить, что кто-то будет действительно читать эти 1000 страниц с формулами, но даже прочтение 1-2 статей оттуда может быть довольно просвещающим занятием.

#квантовая_термодинамика

Фишеровская информация (Fisher information) – величина, часто встречающаяся в современных работах по статистике, термодинамике и квантовой информации.

Представим себе какое-нибудь статистическое распределение p(x, θ) случайной величины x, зависящее от параметра θ. Расхождение Кульбака-Лейблера показывает (см. формулу на рисунке), насколько два распределения при двух значениях θ различимы – сколько бит информации требуется для определения, с каким из них мы имеем дело. Для двух близких распределений она квадратична по малому приращению параметра Δθ, а коэффициент пропорциональности – это и есть фишеровская информация. Она говорит о том, насколько быстро, в статистическом смысле, меняется распределение p(x, θ) при изменении θ.

Смысл этой величине придает и знаменитое неравенство Крамера-Рао: оно говорит о том, что любая процедура получения оценки (θ с крышечкой) параметра θ по статистике p(x, θ) будет давать квадрат ошибки, то есть дисперсию, равную обратной фишеровской информации.

#информация #математика

Вот это чумовая работа: теоретический вывод и экспериментальная визуализация потоков фишеровской информации о любых параметрах – расположении, ориентации, диэлектрических свойствах и т.д. – объектов, получаемой при их облучении электромагнитными волнами.

Как радиолокация, так и наше зрение основываются на том, что объекты облучаются электромагнитной волной, а затем рассеянные или отраженные волны детектируются, и по их свойствам мы пытаемся сделать выводы о каких-то параметрах θ объектов (например, угле поворота, как показано на рисунке). Фишеровская информация (см. предыдущий пост) говорит о точности, с которыми мы можем определить эти параметры, детектируя рассеянные волны.

Авторы вводят, по аналогии с вектором Пойнтинга (потоком энергии на панели (а)), плотность потока информации (b), уравнение непрерывности для нее и выражения для плотности источников информации, генерируемой объектами с диэлектрической проницаемостью ε(r, θ) или поглощаемой ими при Im ε > 0.

#электродинамика #информация #отвал_башки

Вот красивый пример генерации фишеровской информации о горизонтальной координате θ диэлектрического слоя в одномерной геометрии рассеяния.

На диэлектрик слева падает волновой пакет, и на верхних графиках (а) показано, как ведет себя в разные моменты плотность электромагнитной энергии. Мы видим частичное прохождение электромагнитного импульса и частичное его отражение от обеих границ раздела.

Для сравнения, на нижних графиках (b) показано поведение плотности фишеровской информации. Пока импульс не добрался до диэлектрика, она равна нулю. Ее генерация начинается при столкновении импульса с диэлектриком на обеих границах раздела (фиолетовых линиях) – потому что именно их горизонтальные координаты здесь важны.

Примечательно, что плотность информации не идет вправо, интерферируя деструктивно, поскольку амплитуда и фаза прошедшего импульса не зависят от горизонтальной координаты θ диэлектрического слоя. Только отраженный сигнал несет информацию о ней.

#электродинамика #информация #отвал_башки

А вот пример измеренных в эксперименте потоков фишеровской информации, переносимых микроволнами, которыми облучают объект с последующим детектированием отраженных сигналов.

Как показано на панели (a), изучаемый объект – это металлический куб, помещенный в плоский волновод, заполненный дополнительно рассеивающими тефлоновыми цилиндрами. Облучение и детектирование каждый раз оптимизировались для максимизации информации, получаемой либо о горизонтальной (θ = x), либо о вертикальной (θ = y) координатах куба.

Потоки информации в пространстве, восстановленные по измеренному распределению поля, показаны на панелях (b)-(c). Можно видеть, как они распространяются к детектору из мест своей генерации – точек, в которых условия распространения волн наиболее сильно меняются при малых вариациях θ. В случае θ = x это обращенная к источнику и детектору боковая поверхность куба, в случае θ = x – его верхняя и нижняя поверхности.

#электродинамика #информация #отвал_башки

Модель Раби описывает взаимодействие кубита с одной модой электромагнитного поля посредством вращающих и противовращающих членов. Выбрасывая последние, ее часто упрощают до модели Джейнса-Каммингса, обладающей интегралом движения С – полным числом возбуждений. Благодаря наличию этого интеграла, модель Джейнса-Каммингса легко решается аналитически.

В случае модели Раби полное число возбуждений не сохраняется, но зато сохраняется его четность, поскольку противовращающие члены изменяют C на ±2. Оказывается, даже такого интеграла движения – четности C – достаточно для точного аналитического решения модели Раби, которое было впервые найдено в этой работе 2011 года.

Уровни энергии системы положительной и отрицательной четности даются нулями функций G₊(x) и G₋(x), построение которых описано на рисунке. На графике показано, как энергии уровней зависят от константы взаимодействия g. В точках пересечений двух уровней G₊(x) и G₋(x) формально не имеют корней – это особые, исключительные случаи.

#фотоника

Короткими путями к адиабатичности называют протоколы, позволяющие быстро изменить квантовое состояние системы внешними воздействиями без ее возбуждения. В классической термодинамике такое невозможно: к примеру, при быстром или сжатии или расширении газа в сосуде часть работы неизбежно перейдет в тепло.

В этой работе показано, как быстро расширить одномерный квантовый газ, помещенный между жесткими стенками. Для этого, одновременно с расширением стенок по определенному закону ξ(t), нужно действовать на него квадратичным потенциалом Ω²(t)x²/2, помогающим в нужные моменты разгонять или замедлять частицы. Если правильно подобрать зависимости ξ(t) и Ω²(t), можно добиться сжатия газа (желтые кривые) или его расширения (синие и зеленые кривые) без возбуждения.

Диаграммы снизу показывают, как ведет себя плотность энергии при правильном протоколе расширения (слева) и при обычном линейном по времени сдвиге стенки (справа). Во втором случае в газе образуется множество возбуждений.

#квантовая_термодинамика

Кстати, на этих графиках из предыдущего поста наглядно видно, как работают короткие пути к адиабатичности (shortcuts to adiabaticity).

Если мы хотим сжать газ в сосуде, координата его правой стенки ξ(t) сдвигается слева, как показано желтой кривой на верхнем графике. При этом дополнительный квадратичный потенциал Ω²(t)x²/2, действующий на частицы газа, сначала ускоряет их внутрь, к началу координат (Ω² > 0), а затем отталкивает их обратно, чтобы замедлить (Ω² < 0). Получается протокол, аккуратно ускоряющий и замедляющий частицы во избежание генерации возбуждений над основным состоянием газа.

При расширении сосуда (синяя и зеленая кривые) все наоборот: квадратичный потенциал сначала отталкивает частицы подальше от начала координат, где находится левая стенка (Ω² < 0), а под конец становится удерживающим (Ω² > 0), чтобы замедлить их разлет.

#квантовая_термодинамика

Занятная работа с теоретическим предсказанием жидкого топологического изолятора. Это аморфный топологический изолятор, беспорядок в котором не зафиксирован, а динамически меняется и обусловлен тепловым движением его собственных частиц при температурах выше точки плавления решетки.

Автор рассмотрел двумерную модель сильной связи с двумя орбиталями (s и p + ip) на каждом атоме, а сами атомы движутся под действием как сил со стороны электронной подсистемы, так и собственного отталкивания. Как видно на рисунке сверху, при высокой температуре образуется жидкость (a) с плавно осциллирующей парной корреляционной функцией (c), а при низкой температуре – кристалл с треугольной решеткой (b), (d).

Диаграммы снизу показывают щель в спектре (слева) и индекс Ботта ν, заменяющий для неупорядоченной системы индекс Черна (справа), как функции плотности ρ и температуры T. При ρ > 0.2 ненулевая щель в спектре и топологическая нетривиальность (ν = 1) сохраняются даже при высоких температурах.

#топологические_материалы

Любопытный эксперимент с размножением молекул и их «естественным отбором» под влиянием механических воздействий.

Как показано слева, мономеры – бензольные кольца с присоединенными к ним цепочками аминокислот и тиольными группами (SH) – могут соединяться в кольца различного размера (тримеры, тетрамеры, пентамеры, гексамеры, гептамеры и т.д.). Достаточно длинные кольца (гексамеры и гептамеры) могут, в свою очередь, складываться в стопки, формируя нити диаметром около 5 нм, видимые в электронный микроскоп.

По аналогии с биохимическими процессами, составляющими основу жизни, этот процесс автокаталитический: уже образовавшиеся молекулярные комплексы служат катализатором возникновения новых комплексов. Как показано на графиках справа для распределения размеров циклов, получившегося из раствора мономеров спустя 15-20 дней, результаты зависят от условий, в которых они растут и размножаются. Получается, что механическое воздействие служит для молекул внешним фактором отбора.

#самоорганизация #химия

Как известно, атеизм – это тоже религия, а некурящие – тоже курульщики, которые курят отсутствие табака. Вот и авторы этой статьи тоже считают, что отсутствие механического воздействия (перемешивания, встряхивания и т.д.) на сосуд с раствором – это тоже один из режимов механического воздействия.

#цитаты #химия

Отталкивание (антипересечение) энергетических уровней при гибридизации состояний – одно из базовых явлений квантовой механики. А в этом эксперименте наблюдалось противоположное явление притяжения (или схлопывания) уровней.

Оно возникает за счет эффекта Ленца – диссипативного взаимодействия микроволн в резонаторе с магнитным моментом шарика, схожего с явлением магнитного торможения. При таком взаимодействии изменение магнитного момента шарика создает индукционные токи в металлических стенках резонатора, стремящиеся заглушить изменение магнитного потока.

Эффект Ленца создает чисто мнимое расщепление Раби между магнонной модой шарика и электромагнитной модой резонатора. Как следствие, при достаточном сближении их частот вместо двух вещественных собственных значений гамильтониана двухуровневой системы мы получаем два комплексно сопряженных корня. Общая вещественная часть обоих корней дает картину двух «схлопнувшихся» энергетических уровней, которая и наблюдалась в эксперименте.

#квантовая_механика #магнетизм