Вот это крутой эксперимент, в котором наглядно продемонстрированы сверхнизкие значения скорости Ферми в почти плоских зонах двухслойного графена, повернутого на «магический угол», а также необычный характер его сверхпроводимости.

Графики сверху показывают зависимости дифференциальной проводимости от тока, измеренные при различных уровнях допирования ñ. Пики дифференциальной проводимости в нормальном состоянии, при подавлении сверхпроводимости магнитным полем (синие кривые), возникают, когда скорость электронов, переносящих ток J, сравнивается со скоростью Ферми v_F. Измеренные таким образом значения v_F могут доходить до рекордно низких 700 м/с.

В сверхпроводящей фазе (красные кривые) возникают дополнительные пики при критическом токе J_c сверхпроводника. Как демонстрируется на графике снизу, при малых |ñ| критический ток J_c связан с ограничением скорости электронов величиной v_F, а при больших |ñ| – обычным для сверхпроводников условием развала куперовских пар v = Δ/(ħ×k_F).

#сверхпроводимость #графен

А вот еще интересные особенности сверхпроводимости в двухслойном графене, повернутом на «магический угол».

Во-первых, отношение Δ(0)/T_c щели при T = 0 к критической температуре здесь составляет около 0.05 – вместо даваемого теорией БКШ отношения 1.75, типичного для обычных сверхпроводников. Это свидетельствует о необычном характере сверхпроводимости.

Во-вторых, отношение T_c/T_F критической температуры к энергии Ферми T_F здесь больше 1 и может достигать аж 9 (красная кривая на графике слева), в то время как при спаривании в режиме слабой связи оно должно быть много меньше 1. А для электронов с квадратичной дисперсией оно, независимо от механизма спаривания, не может превышать 1/8.

В-третьих, измеренная разными способами сверхтекучая плотность (зеленая и красная кривые на графике справа) во много раз превышает даваемую формулой Ландау (черный пунктир). Это наглядная демонстрация геометрического вклада в сверхтекучую плотность, не учитываемого формулой Ландау.

#сверхпроводимость #графен

Использование чат-ботов наподобие ChatGPT для генерации справочных данных о свойствах и перспективах химических соединений наталкивается на проблему: в литературе, используемой для их обучения, имеется перекос в сторону небольшого числа «хайповых» тем.

В то же время, в научных базах данных (OQMD, Materials Project, JARVIS, COD, AFLOW2) пространство соединений покрывается более равномерно. Для примера можно посмотреть (сверху на рисунке) на частоты встречаемости химических элементов в обоих случаях. В первом случае наблюдается перекос в сторону оксидов, органики и соединений меди и железа.

Авторы этой работы сделали попытку исправить этот перекос, обучив на научных базах данных графовую нейронную сеть, а затем на основе этого (я не понял, как именно) заставив ChatGPT-3.5-turbo генерировать текстовые описания материалов. ChatGPT-4 и эксперты-люди достаточно высоко оценили эти тексты по критериям фактической точности, глубины содержания и правильности языковой структуры.

#нейронные_сети #популярное

Вязкость жидкости η связана с ее способностью к поперечному переносу импульса. Она пропорциональна времени свободного пробега τ квазичастиц, поэтому при низких температурах в ферми-жидкости, когда τ ~ T⁻², вязкость в норме также растет как η ~ T⁻². Но при наличии фазовых переходов на фоне этой зависимости могут возникать особенности.

В этом эксперименте впервые наблюдалось предсказанное почти 50 лет назад резкое уменьшение вязкости жидкого ³He вблизи перехода в сверхтекучее состояние, обусловленное флуктуациями куперовских пар. Вязкость оценивалась как η ~ Q⁻² по сверхчувствительным измерениям добротности Q колебаний кварцевого резонатора в форме вилки, погруженного в ³He. Как видно на графиках для различных давлений, вблизи сверхтекучего перехода рассеяние квазичастиц на флуктуациях куперовских пар резко снижает τ и, как следствие, понижает η и увеличивает Q. Резкий рост добротности Q накладывается на ее обычное фермижидкостное поведение Q ~ T.

#гидродинамика #сверхпроводимость #сверхтекучесть

В этой работе была выведена обобщенная теорема Гельмана-Фейнмана, связывающая малые изменения энергий стационарных состояний с изменениями гамильтониана, для неэрмитовых PT-симметричных систем.

Авторы демонстрируют, что и в PT-симметричной фазе, и в фазе с нарушенной PT-симметрией она имеет один и тот же вид, показанный на рисунке. Здесь |R> и |L> – правые и левые собственные векторы гамильтониана, G – оператор, превращающий правые векторы в левые.

На графиках показан пример сравнения модулей левой и правой частей теоремы, посчитанных для нескольких стационарных состояний двумерного ангармонического осциллятора с неэрмитовой добавкой к гамильтониану iλxy. При λ = 4 имеется исключительная точка, в которой для некоторых состояний производная ∂E/∂λ расходится. Тем не менее, обобщенная теорема Гельмана-Фейнмана всегда продолжает выполняться. Расходимость ∂E/∂λ свидетельствует о высокой чувствительности системы к малым изменениям λ, что само по себе интересно.

#квантовая_механика #неэрмитовы_системы

Знаменитая теорема Гельмана-Фейнмана, представленная формулой (1), конечно же, не была впервые выведена ни Гельманом, ни Фейнманом. Ее получил Поль Гюттингер пятью годами раньше.

#квантовая_механика #цитаты

Красивая визуализация экспериментальных точек на грани искусства.

#цитаты

Аномальное гидравлическое сопротивление – это открытое более 50 лет назад явление, заключающееся в резком увеличении сопротивления потока при просачивании полимерного раствора через пористую среду, когда его скорость превышает некоторый порог. В этой работе наконец-то подтверждена одна из гипотез, объясняющих механизм его возникновения.

Раствор полимера пропускался через пористый массив стеклянных бусинок (A), а равенство их показателей преломления позволило измерять скорость жидкости во всем объеме благодаря флоуресцентным меткам. Аномальное гидравлическое сопротивление можно видеть на панели (B) как резкий рост сопротивления (отношения разности давлений к потоку) при увеличении средней скорости сдвига dγ/dt.

Причина, как показывают авторы – в резком увеличении флуктуаций потока во времени (E)-(F), называемом упругой турбулентностью. Быстрые перестройки поля скоростей уменьшают средний поток и увеличивают гидравлическое сопротивление по сравнению с допороговым ламинарным течением (С)-(D).

#гидродинамика

А вот видео из статьи из предыдущего поста: на нем показано, как с течением времени меняется поле скоростей жидкости, измеренное в одной из пор, при общей скорости потока выше порога. Видно, что оно сильно флуктуирует во времени – это называется упругой турбулентностью.

Это явление отличается от обычной, инерциальной турбулентности, возникающей при высоких числах Рейнольдса (выше 2000-3000) и обусловленной хаотичным движением жидкости по инерции. Здесь число Рейнольдса не превышает 0.0001, так что причина турбулентности иная. Как я понял, она вызвана процессом протаскивания длинных полимерных молекул через пору, которые хаотично сгибаются и перекручиваются.

#гидродинамика

Верхнюю ветвь экситонных поляритонов в оптической полости обычно относят к резервуару – некогерентной системе поляритонов и несвязанных со светом экситонов, служащих фоном для бозе-конденсации нижних поляритонов. А вот недавний эксперимент, в котором наблюдали бозе-конденсацию верхних поляритонов.

Это удалось сделать благодаря сочетанию факторов:
а) нерезонансная накачка преимущественно пополняет верхние поляритоны;
б) из-за отрицательной расстройки верхние поляритоны в большей мере экситонные, чем нижние, поэтому они быстрее термализуются за счет столкновений и медленнее высвечиваются;
в) превращение верхних поляритонов в нижние относительно медленное – верхние поляритоны скорее распадаются (и пополняются накачкой), чем превращаются в нижние.

На рисунке можно видеть характерные черты бозе-конденсации верхних поляритонов: нелинейное увеличение интенсивности при переходе накачки через порог и сужение спектральной линии в пространстве импульсов и энергии.

#поляритоны #бозе_конденсация

Красивая теоретическая работа с выводом набора оптических правил сумм для поляритонных мод в среде с произвольными функциями диэлектрического ε(ω) и магнитного μ(ω) отклика (хотя и не имеющей потерь).

Уравнение дисперсии для света в среде (первое уравнение на рисунке) дает в качестве решения частоты ω_j поляритонных мод. Второе уравнение дает правила сумм: универсальные соотношения для фазовых и групповых скоростей, просуммированных по всем поляритонным модам, где в качестве функции z(ω) может служить каждая из 4 комбинаций оптических констант, указанных ниже.

Из этих правил сумм, в частности, следует, что все поляритонные моды одновременно не могут иметь отрицательные групповые скорости – даже в математериалах с отрицательным показателем преломления. На графиках показан пример поляритонных дисперсий в среде с резонансным поведением ε(ω) и μ(ω): отрицательная групповая скорость одного поляритона компенсируется положительными скоростями двух других.

#электродинамика #поляритоны

Обзор о неравновесных магнитoтранспортных явлениях, происходящих в двумерном электронном газе в слабых или умеренных магнитных полях. Все очень обстоятельно: в статье не только цитируются основные экспериментальные результаты, но и описываются базовые теоретические модели наблюдаемых эффектов.

Самые известные равновесные магнитотранспортные явления – это слабая локализация, осцилляции Шубникова-де Гааза и поправки Альтшулера-Аронова за счет комбинации кулоновского взаимодействия и беспорядка (не говоря о квантовых эффектах Холла, возникающих уже в сильном магнитном поле). Эти явления относятся к статической проводимости, но и в динамической проводимости на частотах порядка одной-нескольких циклотронных частот также возникают квантовые осцилляции, обусловленные дискретностью уровней Ландау.

Неравновесные же магнитотранспортные явления возникают при облучении образцов микроволнами либо при приложении сильного постоянного или переменного тока. Основные из них следующие:
● Microwave-induced resistance oscillations (MIRO) – осцилляции проводимости как функции магнитного поля в образце, облучаемом микроволнами.
● Zero-resistance states (ZRS) – возникновение при облучении микроволнами на зависимости проводимости от магнитного поля участков с нулевым сопротивлением, при которых удельная холловская проводимость, тем не менее, не квантуется (что отличает ZRS от квантового эффекта Холла).
● Hall field-induced resistance oscillations (HIRO) – осцилляции дифференциальной проводимости как функции магнитного поля в образце, через который пропускается постоянный ток.
● Phonon-induced resistance oscillations (PIRO) – осцилляции проводимости как функции магнитного поля, обусловленные электрон-фононным взаимодействием. Здесь собственные фононы образца выступают как эффективные «микроволны», действующие на электроны и приводящие к аналогу эффекта MIRO.
● Дробные аналоги MIRO и HIRO, возникающие в сильных магнитных полях.

#уровни_Ландау #твердое_тело

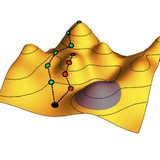
Вот это крутая работа: экспериментальная реализация трехмерного акустического метаматериала с практически плоскими уровнями Ландау. Причем, в отличие от электронов в магнитном поле, где уровни Ландау имеют квадратичную дисперсию в направлении вдоль магнитного поля, здесь акустические уровни Ландау плоские во всех трех измерениях.

Как показано на рисунке, образование таких уровней можно объяснить следующим образом: создается материал со сплошным кольцом дираковских точек (нодальный полуметалл), а неоднородная деформация его кристаллической решетки дает начало эффективному магнитному полю, расщепляющему дисперсию звуковых волн на набор уровней Ландау.

Как можно видеть на графике снизу, дискретные уровни Ландау видны на спектре звукового давления в толще образца как резонансы на соответствующих частотах, при которых звук хорошо распространяется с поверхности в глубину.

#акустика #топологические_материалы #уровни_Ландау

Метод обратной диффузии, которым генерируют изображения большинство современных нейронных сетей, при высоких разрешениях картинки становится вычислительно весьма затратным – потому что приходится рассчитывать диффузию в пространстве изображений x очень высокой размерности.

В этой работе разработан метод обратной диффузии в скрытом пространстве, позволяющий сделать генерацию изображений более быстрой и устойчивой. Для этого авторы сначала на библиотеке изображений обучают автокодировщик. После того, как он научился эффективно сжимать изображения x до меньшего вектора z и распаковывать их обратно без существенных искажений x → z → x´, обратная диффузия осуществляется уже в «скрытом пространстве» векторов z, что позволяет абстрагироваться от несущественных деталей типа цвета каждого конкретного пикселя.

Эту диффузию можно разными способами направлять, генерируя не просто случайные картинки, а изображая определенные сцены, осуществляя апскейлинг, дорисовывая недостающие части и т.д.

#нейронные_сети

Вот примеры того, что происходит при генерации изображений методом обратной диффузии, которая никак не направляется: как показано на картинках справа, получаются малосогласованные повторяющиеся структуры.

Если же направлять диффузию, заставляя нейросеть генерировать изображение, «похожее» на референс меньшего разрешения (картинки слева), получаются более реалистичные картины, демонстрирующие четкую глобальную структуру (картинки в центре).

#нейронные_сети

Это пример семантического синтеза изображений методом обратной диффузии в скрытом пространстве. Нейросеть должна сгенерировать изображение по заданной семантической маске, показанной сверху. Как я понимаю, на красных участках должно быть небо, на серых – деревья, на желтых и салатовых – земля, на зеленых – вода. Ниже идут три примера генерации по этой маске.

Здесь примечательно то, что модель обучалась на изображениях разрешением 256×256, а генерирует изображения более высокого разрешения 1024×384. В этом преимущество метода диффузии в скрытом пространстве: он не привязан к конкретным размерам изображений и может легко масштабироваться.

#нейронные_сети

А вот примеры дорисовывания (inpainting) изображений нейросетью.

Здесь обратная диффузия в скрытом пространстве направляется таким образом, чтобы сгенерированное изображение было максимально похоже на часть исходного изображения за рамками красного контура. В результате получается изображение, на которой фрагмент внутри контура додумывается нейросетью по остальной части картинки.

Так можно удалять с фотографий «лишние» объекты, портящие своим видом красивый фон.

#нейронные_сети

Многомировая интерпретация квантовой механики подразумевает, что при квантовых измерениях история нашей Вселенной делится на ветви, в каждой из которых реализуется свой вариант классической реальности. Но по каким в точности критериям такие ветвления происходят?

Авторы этой работы делают попытку определить ветвление волновой функции, основываясь на операционных понятиях, связанных с трудностью квантовых вычислений. Они ставят следующую задачу: допустим, мы представляем волновую функцию системы |Ψ> = Σᵢcᵢ|ψᵢ> в виде суперпозиции |ψᵢ>. При каком выборе набора векторов |ψᵢ> их когерентную суперпозицию будет сложно отличить на практике от некогерентной смеси? Иными словами, как именно мы можем разветвить волновую функцию на «классические миры», взаимная интерференция между которыми будет практически неизмеримой?

Для ответа на этот вопрос авторы вводят меру трудности детектирования интерференции C_I между двумя состояниями |a> и |b> как минимального числа квантовых гейтов, требуемых для того, чтобы две их суперпозиции {|a>+exp(iθ)|b>}/√2 и {|a>+exp(–iθ)|b>}/√2 с любой относительной фазой θ, после воздействия этих гейтов были достаточно хорошо различимы в плане измерения статистики состояний кубитов в вычислительном базисе. Такая мера говорит о том, насколько трудно, с вычислительной точки зрения, отличить когерентные суперпозиции состояний |a> и |b> от некогерентной смеси.

Однако одной лишь меры C_I недостаточно для определения «хороших» ветвей, поскольку квантовые методы коррекции ошибок позволяют надежно защищать информацию об относительной фазе квантовых состояний. Поэтому авторы налагают дополнительное условие: ветви должны выбираться так, чтобы их можно было относительно легко различить. Для этого вводится мера трудности различимости C_D двух квантовых состояний |a> и |b> как минимальное число квантовых гейтов, требуемых для того, чтобы статистика измерений после воздействия этого набора гейтов на оба состояния достаточно сильно различалась.

Хорошие ветви можно определить как состояния с максимальной разностью C_I – С_D: такие ветви гораздо проще, с практической, квантово-вычислительной точки зрения, различить между собой, чем детектировать их взаимную интерференцию. Пример таких ветвей – это N-кубитные состояния |000…> и |111…> при больших N. Для обнаружения их интерференции нужна квантовая цепь, переворачивающая все N кубитов (чтобы сопоставить цепочку нулей с цепочкой единиц), в то время как для различения этих состояний достаточно измерить состояние любого из кубитов. Таким образом, C_I ~ N, С_D ~ 1, поэтому разность C_I – C_D велика при больших N.

Вообще говоря, введенная мера хорошего ветвления C_I – C_D не является полностью универсальной в том смысле, что она завязана на определение квантовых гейтов – локальных в некотором вычислительном базисе, – и на введение самого этого базиса. А значит, она завязана на структуру кубитов, из которых состоит рассматриваемая квантовая система: какие именно базисные состояния приписываются отдельным кубитам и как эти кубиты соседствуют друг с другом (таким образом, что, к примеру, двухкубитные операции действуют только на пары близко расположенных кубитов). Но это вряд ли можно считать серьезным недостатком, поскольку и эффективное формирование классической реальности, наблюдаемое в нашей жизни, также завязано на локальность в пространстве.

Операционное определение меры хорошего ветвления является некоторой альтернативой знаменитого einselection (environment-induced superselection) – ветвления историй квантовой системы за счет запутывания с окружением и последующей декогеренции. Примечательно, что эта величина C_I – С_D, как правило, только возрастает при эволюции ветвей с течением времени под действием типичных локальных гамильтонианов. А значит, ветвление волновой функции практически необратимо, не исключением немногих, аномальных случаев.

#квантовая_механика #квантовые_вычисления

Любопытный эксперимент, в котором в гетероструктуре графена и двумерного WS₂ были обнаружены плазмонные поляроны: электронные состояния в полупроводниковом WS₂, «одетые» в шубу виртуальных плазмонов графена.

Для этого авторы изготовили и исследовали ARPES два варианта образцов. В первом варианте (а) слой WS₂ допирован калием до заселения электронами дна зоны проводимости, сигнал от которого показан на панелях (c)-(d). Второй вариант образца – это слой WS₂, на котором сверху лежит слой графена, также допированный калием. Как видно на панелях (e)-(f), в этом случае от дна зоны проводимости отщепляется цепочка дополнительных спектральных полос более низких энергий.

Как показано снизу, наблюдаемые расщепления зависят от уровня допирования электронами n как √n. Это типично для закона дисперсии двумерных плазмонов графена E ~ √n√q, что авторы считают доказательством плазмонного происхождения дополнительных пиков – хотя и непонятно, чему здесь равен q.

#плазмоны #дихалькогениды_переходных_металлов

В системе двух близко расположенных металлических слоев плазмонные моды, как известно, расщепляются на акустическую (антисимметричную суперпозицию плазменных колебаний в двух слоях) и оптическую (симметричную суперпозицию).

В этой теоретической работе гибридизация двух плазмонных мод в бислое рассматривается с квантовомеханической точки зрения, как задача о двух связанных квантовых гармонических осцилляторах. Она решается преобразованиями Хопфилда-Боголюбова, перемешивающих операторы рождения aᵀ⁺, aᴮ⁺ и уничтожения aᵀ, aᴮ плазмонов в обоих слоях. Как результат, основное состояние бислоя оказывается вакуумом для гибридизованных акустических и оптических плазмонов, но не для отдельных плазмонов каждого слоя, так что в нем отличны от нуля средние значения вида <aᵀ⁺aᵀ >, < aᵀaᴮ> и т.д.

Обнаружить их, в принципе, можно по аналогии с динамическим эффектом Казимира: резкое измерение параметров системы (например, уровня допирования одного из слоев) должно приводить к рождению плазмонов «из вакуума».

#плазмоны

Когерентные машины Изинга – это относительно недавно изобретенные квантово-оптические устройства, которые также называют квантовыми нейронными сетями. Их основа – цепочка лазерных импульсов, бегающих по кругу в длинном оптоволокне и подвергающихся оптической накачке благодаря параметрическому рассеянию. Связывая лазерные импульсы между собой оптическими или оптоэлектронными способами, можно моделировать систему взаимодействующих спинов.

Ряд экспериментов показал, что когерентные машины Изинга способны быстро решать оптимизационные задачи, находя основное состояние системы взаимодействующих спинов и успешно конкурируя в этом плане с машинами D-Wave для квантового отжига – а то и превосходя их. Однако, как и в случае машин для квантового отжига, исследователи еще не до конца понимают, каковы пределы возможностей когерентных машин Изинга и в какой мере они используют квантовое превосходство.

В этой статье я постарался максимально понятно объяснить принцип работы когерентных машин Изинга, не вдаваясь в излишние техническое детали:
https://telegra.ph/Kogerentnye-mashiny-Izinga-kvantovye-nejronnye-seti-bystro-reshayushchie-zadachi-optimizacii-09-03

#оптимизация #фотоника #нейронные_сети #квантовые_вычисления