Существует поверье, что в режиме квантового эффекта Холла все токи между контактами переносятся исключительно магнитными краевыми каналами, потому что толща двумерного электронного газа в этом режиме является изолирующей. В этой статье Дэвид Таулес напоминает, что это не так и часть токов может переноситься толщей. Изолирующий характер толщи этому не мешает, поскольку речь идет о холловских токах, а не об обычной, диагональной проводимости.

Как показано на рисунке, если между двумя контактами электрический ток переносится слева направо магнитными краевыми каналами (фиолетовые стрелочки), то один из них – текущий вдоль тока – оказывается более населенным электронами, чем текущий в противоположную сторону. Из-за дисбаланса населенностей краевых каналов возникает электрическое поле (зеленые стрелки), которое, за счет холловской проводимости толщи, дает холловские токи, показанные пунктиром. В типичных условиях через толщу может проходить около 20% суммарного тока.

#уровни_Ландау #объяснения

В этом эксперименте реализованы аналоговые квантовые вычисления с двумерными массивами до 256 ридберговских атомов, каждый из которых является кубитом.

Как показано на рисунке, в массив оптических пинцетов загружаются атомы, которые затем уплотняются, чтобы не было пропусков. Каждый атом может находиться в суперпозиции основного |g> и ридберговского возбужденного |r> состояний, которые управляемо связываются двухфотонными переходами. Близко расположенные атомы при этом связаны ридберговской блокадой: нахождение одного атома в состоянии |r> сдвигает, за счет взаимодействия Ван-дер-Ваальса, уровни энергии соседних атомов, так что их переходы |g> → |r> выходят из резонанса.

Справа показан пример моделирования антиферромагнитной модели Изинга: ридберговская блокада мешает одновременно возбуждаться ближайшим соседям, так что атомы устанавливаются в состояниях |e> и |g> в шахматном порядке.

#атомные_газы #квантовые_вычисления

А вот еще интересный пример аналогового квантового моделирования из статьи из предыдущего поста.

Здесь, как показано на панелях (a)-(c), радиус ридберговской блокады постепенно увеличивается (точнее, он остается постоянным, просто сжимается массив атомов). Слева показана наблюдаемая картина люминесценции атомов: находящиеся в состоянии |g> испускают сигнал и видны как зеленые точки, а атомы в состоянии |e> остаются темными (красные круги). Справа показан фурье-образ <F(k)> корреляционной функции плотности.

Сначала ридберговская блокада захватывает лишь ближайших соседей, так что устанавливается «антиферромагнитная» шахматная фаза (a). Затем, когда блокада достигает соседей 2-го порядка по диагонали устанавливается полосатая фаза (b), а при еще большем ее радиусе возникает звездчатая фаза (c). На панелях (d)-(e) показаны экспериментальная и теоретическая фазовые диаграммы, отслеживаемые по пикам <F(k)>, амплитуды которых играют роль параметров порядка.

#атомные_газы #квантовые_вычисления

Машина Больцмана – это рекуррентная нейронная сеть, у которой сигнал снимается только с части нейронов, называемых видимыми. Остальные нейроны являются скрытыми, а сигналы на всех нейронах бинарны (±1) и генерируются их вероятностной активацией. В ограниченных машинах Больцмана (RBM) соединения имеются только между видимыми и скрытыми нейронами.

Обученная машина Больцмана генерирует некоторую статистику многомерных векторов сигналов на видимых нейронах x. Распределение таких векторов легко записать аналитически (см. формулу на рисунке): это просто общее распределение состояний видимых x и скрытых h нейронов, просуммированное по состояниям последних.

Но легко записать – это еще не значит легко посчитать. Авторы этой работы доказывают, что задача имитации работы RBM на классическом компьютере является экспоненциально трудной. А именно, трудно как оценить вероятность выпадения любого заданного вектора x, так и генерировать векторы x с приближенной статистикой, близкой к оригинальной.

#нейронные_сети

Красивый эксперимент с наблюдением сильной связи магнонов в шариках железо-иттриевого граната с электромагнитными модами микроволнового резонатора.

Резонатор представляет собой металлический цилиндр с двумя столбиками внутри, немного не доходящими до верха. В такой структуре, называемой возвратной полостью, возникают две моды, показанные на рисунке. У темной моды (слева) магнитные поля, создаваемые вертикальными токами в столбиках, почти компенсируют друг друга в месте расположения ферромагнитного шарика. У светлой моды магнитные поля от столбиков складываются в центре полости.

На диаграмме снизу показано поляритонное расщепление линий поглощения как функция магнитного поля, позволяющего регулировать резонансную частоту магнонов. Магнонная мода M1, отвечающая однородной по шарику намагниченности, связывается со светлой модой резонатора (21 ГГц), но не с темной (14 ГГц). С темной же модой связываются (хоть и слабо) магнонные моды M2, M3 с неоднородными распределениями намагниченности.

#поляритоны #магнетизм

Вот красивая идея использования неравновесной системы в качестве демона Максвелла, позволяющего превращать тепло в работу или перекачивать тепло от холодного резервуара к горячему. В отличие от обычного демона Максвелла, проводящего над системой измерения и затем осуществляющего обратную связь, здесь неравновесная система ничего такого не делает, поэтому авторы называют ее N-демоном.

Идея показана на рисунке сверху: N-демон запускает в рабочее тело неравновесно распределенные частицы – отдельно «холодные» и «горячие» (синие и красные), забирая обратно равновесно распределенные (фиолетовые). Если суммарные потоки числа частиц и энергии между рабочим телом и N-демоном равны нулю, то последний является лишь поставщиком «неравновесности» – точнее, негэнтропии.

Глобально второе начало термодинамики здесь не нарушается, поскольку положительное производство энтропии внутри N-демона перекрывает ее отрицательное производство в рабочем теле и связанных с ним резервуарах.

#стохастическая_термодинамика

А вот варианты реализации N-демона, предлагаемые авторами стати из предыдущего поста и позволяющие понять, как в принципе эта штука может работать.

Слева показана электронная реализация, основанная на двумерном электронном газе с магнитными краевыми каналами, присоединенным к четырем контактам. Верхняя часть системы представляет собой N-демона. Его назначение – запускать в нижнюю часть (рабочее тело) существенно неравновесное распределение электронов по энергии f_N(E), отличающееся от распределения Ферми-Дирака. Это достигается наложением «горячего» распределения Ферми-Дирака (электронов, идущих от красного контакта) и «холодного» распределения (от синего контакта), пропускаемых через туннельный переход с коэффициентом пропускания T_d(E), существенно зависящим от энергий.

Справа показана фотонная реализация, где, для аналогичных целей, используются полупрозрачные зеркала с коэффициентом пропускания, существенно зависящим от длины волны.

#стохастическая_термодинамика

Электрон, падающий из нормального металла на границу со сверхпроводником, претерпевает андреевское отражение, если его энергия лежит внутри щели. При этом после поглощении электрона сверхпроводником из последнего вылетает дырка. Андреевское отражение является не зеркальным (specular reflection), а обратным (retroreflection): траектория дырки повторяет траекторию электрона в обратном порядке.

В этой работе теоретически рассмотрен аналог андреевского отражения от бозе-конденсата экситонных поляритонов, в спектре возбуждений которых из-за резонансной накачки имеется щель.

На панели (a) показаны режимы отражения в зависимости от энергии поляритона E, падающего из нормальной области на бозе-конденсированную, и от угла падения θ_I. Возможны режимы отражения частицы без пропускания (b), отражения с пропусканием (d) или полного перехода частицы в распространяющуюся вдоль границы эванесцентную волну без отражения и без пропускания (c).

#поляритоны #бозе_конденсация #сверхпроводимость

Вот это крутой эксперимент, в котором наглядно продемонстрированы сверхнизкие значения скорости Ферми в почти плоских зонах двухслойного графена, повернутого на «магический угол», а также необычный характер его сверхпроводимости.

Графики сверху показывают зависимости дифференциальной проводимости от тока, измеренные при различных уровнях допирования ñ. Пики дифференциальной проводимости в нормальном состоянии, при подавлении сверхпроводимости магнитным полем (синие кривые), возникают, когда скорость электронов, переносящих ток J, сравнивается со скоростью Ферми v_F. Измеренные таким образом значения v_F могут доходить до рекордно низких 700 м/с.

В сверхпроводящей фазе (красные кривые) возникают дополнительные пики при критическом токе J_c сверхпроводника. Как демонстрируется на графике снизу, при малых |ñ| критический ток J_c связан с ограничением скорости электронов величиной v_F, а при больших |ñ| – обычным для сверхпроводников условием развала куперовских пар v = Δ/(ħ×k_F).

#сверхпроводимость #графен

А вот еще интересные особенности сверхпроводимости в двухслойном графене, повернутом на «магический угол».

Во-первых, отношение Δ(0)/T_c щели при T = 0 к критической температуре здесь составляет около 0.05 – вместо даваемого теорией БКШ отношения 1.75, типичного для обычных сверхпроводников. Это свидетельствует о необычном характере сверхпроводимости.

Во-вторых, отношение T_c/T_F критической температуры к энергии Ферми T_F здесь больше 1 и может достигать аж 9 (красная кривая на графике слева), в то время как при спаривании в режиме слабой связи оно должно быть много меньше 1. А для электронов с квадратичной дисперсией оно, независимо от механизма спаривания, не может превышать 1/8.

В-третьих, измеренная разными способами сверхтекучая плотность (зеленая и красная кривые на графике справа) во много раз превышает даваемую формулой Ландау (черный пунктир). Это наглядная демонстрация геометрического вклада в сверхтекучую плотность, не учитываемого формулой Ландау.

#сверхпроводимость #графен

Использование чат-ботов наподобие ChatGPT для генерации справочных данных о свойствах и перспективах химических соединений наталкивается на проблему: в литературе, используемой для их обучения, имеется перекос в сторону небольшого числа «хайповых» тем.

В то же время, в научных базах данных (OQMD, Materials Project, JARVIS, COD, AFLOW2) пространство соединений покрывается более равномерно. Для примера можно посмотреть (сверху на рисунке) на частоты встречаемости химических элементов в обоих случаях. В первом случае наблюдается перекос в сторону оксидов, органики и соединений меди и железа.

Авторы этой работы сделали попытку исправить этот перекос, обучив на научных базах данных графовую нейронную сеть, а затем на основе этого (я не понял, как именно) заставив ChatGPT-3.5-turbo генерировать текстовые описания материалов. ChatGPT-4 и эксперты-люди достаточно высоко оценили эти тексты по критериям фактической точности, глубины содержания и правильности языковой структуры.

#нейронные_сети #популярное

Вязкость жидкости η связана с ее способностью к поперечному переносу импульса. Она пропорциональна времени свободного пробега τ квазичастиц, поэтому при низких температурах в ферми-жидкости, когда τ ~ T⁻², вязкость в норме также растет как η ~ T⁻². Но при наличии фазовых переходов на фоне этой зависимости могут возникать особенности.

В этом эксперименте впервые наблюдалось предсказанное почти 50 лет назад резкое уменьшение вязкости жидкого ³He вблизи перехода в сверхтекучее состояние, обусловленное флуктуациями куперовских пар. Вязкость оценивалась как η ~ Q⁻² по сверхчувствительным измерениям добротности Q колебаний кварцевого резонатора в форме вилки, погруженного в ³He. Как видно на графиках для различных давлений, вблизи сверхтекучего перехода рассеяние квазичастиц на флуктуациях куперовских пар резко снижает τ и, как следствие, понижает η и увеличивает Q. Резкий рост добротности Q накладывается на ее обычное фермижидкостное поведение Q ~ T.

#гидродинамика #сверхпроводимость #сверхтекучесть

В этой работе была выведена обобщенная теорема Гельмана-Фейнмана, связывающая малые изменения энергий стационарных состояний с изменениями гамильтониана, для неэрмитовых PT-симметричных систем.

Авторы демонстрируют, что и в PT-симметричной фазе, и в фазе с нарушенной PT-симметрией она имеет один и тот же вид, показанный на рисунке. Здесь |R> и |L> – правые и левые собственные векторы гамильтониана, G – оператор, превращающий правые векторы в левые.

На графиках показан пример сравнения модулей левой и правой частей теоремы, посчитанных для нескольких стационарных состояний двумерного ангармонического осциллятора с неэрмитовой добавкой к гамильтониану iλxy. При λ = 4 имеется исключительная точка, в которой для некоторых состояний производная ∂E/∂λ расходится. Тем не менее, обобщенная теорема Гельмана-Фейнмана всегда продолжает выполняться. Расходимость ∂E/∂λ свидетельствует о высокой чувствительности системы к малым изменениям λ, что само по себе интересно.

#квантовая_механика #неэрмитовы_системы

Знаменитая теорема Гельмана-Фейнмана, представленная формулой (1), конечно же, не была впервые выведена ни Гельманом, ни Фейнманом. Ее получил Поль Гюттингер пятью годами раньше.

#квантовая_механика #цитаты

Красивая визуализация экспериментальных точек на грани искусства.

#цитаты

Аномальное гидравлическое сопротивление – это открытое более 50 лет назад явление, заключающееся в резком увеличении сопротивления потока при просачивании полимерного раствора через пористую среду, когда его скорость превышает некоторый порог. В этой работе наконец-то подтверждена одна из гипотез, объясняющих механизм его возникновения.

Раствор полимера пропускался через пористый массив стеклянных бусинок (A), а равенство их показателей преломления позволило измерять скорость жидкости во всем объеме благодаря флоуресцентным меткам. Аномальное гидравлическое сопротивление можно видеть на панели (B) как резкий рост сопротивления (отношения разности давлений к потоку) при увеличении средней скорости сдвига dγ/dt.

Причина, как показывают авторы – в резком увеличении флуктуаций потока во времени (E)-(F), называемом упругой турбулентностью. Быстрые перестройки поля скоростей уменьшают средний поток и увеличивают гидравлическое сопротивление по сравнению с допороговым ламинарным течением (С)-(D).

#гидродинамика

А вот видео из статьи из предыдущего поста: на нем показано, как с течением времени меняется поле скоростей жидкости, измеренное в одной из пор, при общей скорости потока выше порога. Видно, что оно сильно флуктуирует во времени – это называется упругой турбулентностью.

Это явление отличается от обычной, инерциальной турбулентности, возникающей при высоких числах Рейнольдса (выше 2000-3000) и обусловленной хаотичным движением жидкости по инерции. Здесь число Рейнольдса не превышает 0.0001, так что причина турбулентности иная. Как я понял, она вызвана процессом протаскивания длинных полимерных молекул через пору, которые хаотично сгибаются и перекручиваются.

#гидродинамика

Верхнюю ветвь экситонных поляритонов в оптической полости обычно относят к резервуару – некогерентной системе поляритонов и несвязанных со светом экситонов, служащих фоном для бозе-конденсации нижних поляритонов. А вот недавний эксперимент, в котором наблюдали бозе-конденсацию верхних поляритонов.

Это удалось сделать благодаря сочетанию факторов:
а) нерезонансная накачка преимущественно пополняет верхние поляритоны;
б) из-за отрицательной расстройки верхние поляритоны в большей мере экситонные, чем нижние, поэтому они быстрее термализуются за счет столкновений и медленнее высвечиваются;
в) превращение верхних поляритонов в нижние относительно медленное – верхние поляритоны скорее распадаются (и пополняются накачкой), чем превращаются в нижние.

На рисунке можно видеть характерные черты бозе-конденсации верхних поляритонов: нелинейное увеличение интенсивности при переходе накачки через порог и сужение спектральной линии в пространстве импульсов и энергии.

#поляритоны #бозе_конденсация

Красивая теоретическая работа с выводом набора оптических правил сумм для поляритонных мод в среде с произвольными функциями диэлектрического ε(ω) и магнитного μ(ω) отклика (хотя и не имеющей потерь).

Уравнение дисперсии для света в среде (первое уравнение на рисунке) дает в качестве решения частоты ω_j поляритонных мод. Второе уравнение дает правила сумм: универсальные соотношения для фазовых и групповых скоростей, просуммированных по всем поляритонным модам, где в качестве функции z(ω) может служить каждая из 4 комбинаций оптических констант, указанных ниже.

Из этих правил сумм, в частности, следует, что все поляритонные моды одновременно не могут иметь отрицательные групповые скорости – даже в математериалах с отрицательным показателем преломления. На графиках показан пример поляритонных дисперсий в среде с резонансным поведением ε(ω) и μ(ω): отрицательная групповая скорость одного поляритона компенсируется положительными скоростями двух других.

#электродинамика #поляритоны

Обзор о неравновесных магнитoтранспортных явлениях, происходящих в двумерном электронном газе в слабых или умеренных магнитных полях. Все очень обстоятельно: в статье не только цитируются основные экспериментальные результаты, но и описываются базовые теоретические модели наблюдаемых эффектов.

Самые известные равновесные магнитотранспортные явления – это слабая локализация, осцилляции Шубникова-де Гааза и поправки Альтшулера-Аронова за счет комбинации кулоновского взаимодействия и беспорядка (не говоря о квантовых эффектах Холла, возникающих уже в сильном магнитном поле). Эти явления относятся к статической проводимости, но и в динамической проводимости на частотах порядка одной-нескольких циклотронных частот также возникают квантовые осцилляции, обусловленные дискретностью уровней Ландау.

Неравновесные же магнитотранспортные явления возникают при облучении образцов микроволнами либо при приложении сильного постоянного или переменного тока. Основные из них следующие:
● Microwave-induced resistance oscillations (MIRO) – осцилляции проводимости как функции магнитного поля в образце, облучаемом микроволнами.
● Zero-resistance states (ZRS) – возникновение при облучении микроволнами на зависимости проводимости от магнитного поля участков с нулевым сопротивлением, при которых удельная холловская проводимость, тем не менее, не квантуется (что отличает ZRS от квантового эффекта Холла).
● Hall field-induced resistance oscillations (HIRO) – осцилляции дифференциальной проводимости как функции магнитного поля в образце, через который пропускается постоянный ток.
● Phonon-induced resistance oscillations (PIRO) – осцилляции проводимости как функции магнитного поля, обусловленные электрон-фононным взаимодействием. Здесь собственные фононы образца выступают как эффективные «микроволны», действующие на электроны и приводящие к аналогу эффекта MIRO.
● Дробные аналоги MIRO и HIRO, возникающие в сильных магнитных полях.

#уровни_Ландау #твердое_тело

Вот это крутая работа: экспериментальная реализация трехмерного акустического метаматериала с практически плоскими уровнями Ландау. Причем, в отличие от электронов в магнитном поле, где уровни Ландау имеют квадратичную дисперсию в направлении вдоль магнитного поля, здесь акустические уровни Ландау плоские во всех трех измерениях.

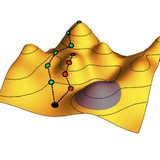
Как показано на рисунке, образование таких уровней можно объяснить следующим образом: создается материал со сплошным кольцом дираковских точек (нодальный полуметалл), а неоднородная деформация его кристаллической решетки дает начало эффективному магнитному полю, расщепляющему дисперсию звуковых волн на набор уровней Ландау.

Как можно видеть на графике снизу, дискретные уровни Ландау видны на спектре звукового давления в толще образца как резонансы на соответствующих частотах, при которых звук хорошо распространяется с поверхности в глубину.

#акустика #топологические_материалы #уровни_Ландау