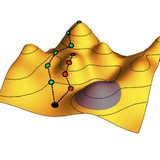
Недавно я писал о теории сверхпроводимости и сверхтекучести в материалах с плоскими зонами, в которых важную роль начинает играть геометрия квантовых состояний – хотя бы потому, что в случае полностью плоской зоны обычная формула Ландау для сверхтекучей плотности дает нулевой результат.
В этой работе подробно расписано, как сверхтекучая плотность сверхпроводника D рассчитывается в обобщенном приближении хаотических фаз. Она находится как вторая производная ∂²Ω/∂A² термодинамического потенциала Ω по векторному потенциалу A, где Ω считается в приближении среднего поля, в котором вводится щель Δ, выраженная через аномальные квазисредние.
Ключевой момент здесь в том, что при таком расчете, по-хорошему, нужно учитывать, что сама щель Δ тоже зависит от векторного потенциала A. Обычно при расчетах функций отклика сверхпроводника этой зависимостью пренебрегают, что авторы называют, собственно, «приближением среднего поля». В этом приближении находится лишь часть D⁽⁰⁾ сверхтекучей плотности. Вторая ее часть D⁽¹⁾ – это поправка, обусловленная зависимостью возмущением щели векторным потенциалом. В учете этой поправки и заключается, в терминологии авторов, обобщение приближения хаотических фаз.
Также в статье показано, что каждая часть D⁽⁰⁾ и D⁽¹⁾ сверхтекучей плотности раскладывается на «обычный» и геометрический вклады. Обычные вклады зависят только от дисперсии квазичастиц и для D⁽⁰⁾ он дается традиционной формулой Ландау. Геометрические же вклады зависят не только от дисперсии квазичастиц, но и от квантовой метрики электронных состояний по всей первой зоне Бриллюэна.
Еще одно интересное понятие, обсуждаемое в статье – так называемая минимальная квантовая метрика. Дело в том, что при построении электронных состояний в кристалле координаты атомных орбиталей Rᵢ в элементарной ячейке можно формально менять (даже если в действительности атомы не сдвигаются и все интегралы перескока сохраняются) – они входят в факторы exp(ikRᵢ) при построении блоховских волн в кристалле и поэтому меняют волновые функции.
Координаты орбиталей можно так оптимизировать, чтобы интегральная по всей зоне Бриллюэна квантовая метрика получившихся электронных состояний была минимальна. При этом поправка D⁽¹⁾ за пределами среднего поля к сверхтекучей плотности обращается в ноль. А координаты орбиталей, минимизирующие метрику, называются естественным положением орбиталей.
#сверхтекучесть #сверхпроводимость #топологические_материалы
В этой работе подробно расписано, как сверхтекучая плотность сверхпроводника D рассчитывается в обобщенном приближении хаотических фаз. Она находится как вторая производная ∂²Ω/∂A² термодинамического потенциала Ω по векторному потенциалу A, где Ω считается в приближении среднего поля, в котором вводится щель Δ, выраженная через аномальные квазисредние.
Ключевой момент здесь в том, что при таком расчете, по-хорошему, нужно учитывать, что сама щель Δ тоже зависит от векторного потенциала A. Обычно при расчетах функций отклика сверхпроводника этой зависимостью пренебрегают, что авторы называют, собственно, «приближением среднего поля». В этом приближении находится лишь часть D⁽⁰⁾ сверхтекучей плотности. Вторая ее часть D⁽¹⁾ – это поправка, обусловленная зависимостью возмущением щели векторным потенциалом. В учете этой поправки и заключается, в терминологии авторов, обобщение приближения хаотических фаз.
Также в статье показано, что каждая часть D⁽⁰⁾ и D⁽¹⁾ сверхтекучей плотности раскладывается на «обычный» и геометрический вклады. Обычные вклады зависят только от дисперсии квазичастиц и для D⁽⁰⁾ он дается традиционной формулой Ландау. Геометрические же вклады зависят не только от дисперсии квазичастиц, но и от квантовой метрики электронных состояний по всей первой зоне Бриллюэна.
Еще одно интересное понятие, обсуждаемое в статье – так называемая минимальная квантовая метрика. Дело в том, что при построении электронных состояний в кристалле координаты атомных орбиталей Rᵢ в элементарной ячейке можно формально менять (даже если в действительности атомы не сдвигаются и все интегралы перескока сохраняются) – они входят в факторы exp(ikRᵢ) при построении блоховских волн в кристалле и поэтому меняют волновые функции.
Координаты орбиталей можно так оптимизировать, чтобы интегральная по всей зоне Бриллюэна квантовая метрика получившихся электронных состояний была минимальна. При этом поправка D⁽¹⁾ за пределами среднего поля к сверхтекучей плотности обращается в ноль. А координаты орбиталей, минимизирующие метрику, называются естественным положением орбиталей.
#сверхтекучесть #сверхпроводимость #топологические_материалы
Telegram
Бассейн эргодичности
Познавательный обзор о теории сверхпроводимости и сверхтекучести, возникающей на плоских энергетических зонах. Такая теория была развита в последние годы в связи с популярностью плоскозонных материалов.
Когда энергетическая зона является плоской, изменение…
Когда энергетическая зона является плоской, изменение…
👍2
А вот иллюстрация того, как работают процедура правильного вычисления сверхтекучей плотности и концепция естественных положений орбиталей на примере модели Су-Шриффера-Хеегера (SSH).
Как показано на верхнем рисунке, это одномерная цепочка атомов с чередующимися перескоками w и v. Если положить w = 0 (рисунок в центре) либо v = 0 (снизу), энергетическая зона становится полностью плоской. И в обоих этих случаях сверхтекучая плотность D, очевидно, должна быть равна нулю – потому что цепочка распадается на димеры. Однако, если посчитать сверхтекучую плотность в приближении среднего поля, мы получим D = 0 в первом случае, но D > 0 во втором.
Парадокс разрешается учетом поправок за пределами среднего поля, которые делают суммарную D нулевой. Причина аномальности второго случая в том, что для него естественные положения орбиталей (красный прямоугольник) не совпадают с координатами двух атомов, принимаемыми в расчет при нахождении зонной структуры.
#сверхтекучесть #сверхпроводимость #топологические_материалы
Как показано на верхнем рисунке, это одномерная цепочка атомов с чередующимися перескоками w и v. Если положить w = 0 (рисунок в центре) либо v = 0 (снизу), энергетическая зона становится полностью плоской. И в обоих этих случаях сверхтекучая плотность D, очевидно, должна быть равна нулю – потому что цепочка распадается на димеры. Однако, если посчитать сверхтекучую плотность в приближении среднего поля, мы получим D = 0 в первом случае, но D > 0 во втором.
Парадокс разрешается учетом поправок за пределами среднего поля, которые делают суммарную D нулевой. Причина аномальности второго случая в том, что для него естественные положения орбиталей (красный прямоугольник) не совпадают с координатами двух атомов, принимаемыми в расчет при нахождении зонной структуры.
#сверхтекучесть #сверхпроводимость #топологические_материалы
Поляритонный лазер с электрической накачкой, реализованный в этой работе, создает когерентный поток фотонов благодаря соединению накачиваемых электронов и дырок в экситоны, которые затем превращаются в термализованные поляритоны.
Как можно видеть на рисунке, по мере увеличения тока накачки j система проходит через три режима. При токе ниже первого порога происходит обычная некогерентная электролюминесценция, то есть система работает как светодиод. Выше первого порога устанавливается режим поляритонного лазера: поляритонный газ служит активной средой для фотонов, а зеемановское расщепление спектральной линии в магнитном поле, показанное звездочками, частично подавляются нелинейными эффектами.
Выше второго порога система, как утверждают авторы, переходит в режим обычного лазера в режиме слабой связи, а зеемановское расщепление полностью подавляется. Но и поляритоны при этом бозе-конденсируются, так что я не особо понял, как конденсация поляритонов состыкуется с режимом слабой связи.
#экситоны #поляритоны
Как можно видеть на рисунке, по мере увеличения тока накачки j система проходит через три режима. При токе ниже первого порога происходит обычная некогерентная электролюминесценция, то есть система работает как светодиод. Выше первого порога устанавливается режим поляритонного лазера: поляритонный газ служит активной средой для фотонов, а зеемановское расщепление спектральной линии в магнитном поле, показанное звездочками, частично подавляются нелинейными эффектами.
Выше второго порога система, как утверждают авторы, переходит в режим обычного лазера в режиме слабой связи, а зеемановское расщепление полностью подавляется. Но и поляритоны при этом бозе-конденсируются, так что я не особо понял, как конденсация поляритонов состыкуется с режимом слабой связи.
#экситоны #поляритоны
«После второго перехода в режим слабой связи зеемановское расщепление оказывается полностью отбеленным» – что-то авторы статьи переборщили со своим жаргоном.
Имелось в виду, что зеемановское расщепление полностью подавляется из-за эффекта оптического отбеливания (или обесцвечивания), при котором электронные переходы в материале, ответственные за поглощение, насыщаются, так что материал перестает поглощать дальнейшее излучение этой же частоты.
#фотоника #цитаты
Имелось в виду, что зеемановское расщепление полностью подавляется из-за эффекта оптического отбеливания (или обесцвечивания), при котором электронные переходы в материале, ответственные за поглощение, насыщаются, так что материал перестает поглощать дальнейшее излучение этой же частоты.
#фотоника #цитаты
Теорема Блоха, как известно, устанавливает форму волновой функции частицы в периодическом потенциале: это произведение плоской волны на периодическую функцию. Но есть и другая теорема, также известная как теорема Блоха, согласно которой в основном состоянии любой квантовой системы должны отсутствовать токи. В этой статье 1949 года Дэвид Бом дает простое и элегантное доказательство такой теоремы.
Оно делается от противного: представим, что в системе с волновой функций основного состояния ψ есть ненулевой средний ток j₀. Тогда умножим ψ на exp(iP•Σᵢrᵢ/ℏ), где rᵢ – координаты всех электронов. Это отвечает приданию системе дополнительного импульса центра масс P, которое меняет только суммарную кинетическую энергию всех частиц, не влияя на энергию межчастичных взаимодействий.
Если направить импульс P противоположно вектору j₀ и сделать его достаточно малым по модулю, то, как легко посчитать в две строчки, средняя по новой волновой функции кинетическая энергия уменьшится на величину e(j₀•P)/m – а значит, уменьшится и полная энергия системы. Но это противоречит предположению о том, что исходная волновая функция ψ была основным состоянием. Ведь любое изменение волновой функции по сравнению с основным состоянием может только увеличить энергию или оставить ее прежней. Отсюда следует, что средний ток в основном состоянии j₀ не может быть отличным от нуля.
Стоит заметить только, что это доказательство вряд ли будет работать, если система заполняет неодносвязную область пространства – например, кольцо. В этом случае из-за периодических граничных условий, налагаемых на волновую функцию при обходе вокруг кольца, мы не можем умножить ψ на exp(iP•Σᵢrᵢ/ℏ) с произвольно малым импульсом P, поскольку он должен квантоваться. Это объясняет наличие незатухающих токов в основном состоянии в небольших кольцах, изготовленных как из нормальных металлов, так и из сверхпроводников, через которые пропущено магнитное поле: теорема Блоха для них неприменима.
Еще большой вопрос, насколько теорема Блоха применима для систем с отсутствующей галилеевой инвариантностью, таких как материалы с бесмассовыми дираковскими и прочими экзотическими электронами. Строго говоря, любые электроны в кристалле не обладают галилеевой инвариантностью, поскольку при вышеописанном построении мы придаем импульс P только электронам, оставляя решетку на месте, так что здесь нужна определенная осмотрительность.
#твердое_тело #сверхпроводимость #объяснения
Оно делается от противного: представим, что в системе с волновой функций основного состояния ψ есть ненулевой средний ток j₀. Тогда умножим ψ на exp(iP•Σᵢrᵢ/ℏ), где rᵢ – координаты всех электронов. Это отвечает приданию системе дополнительного импульса центра масс P, которое меняет только суммарную кинетическую энергию всех частиц, не влияя на энергию межчастичных взаимодействий.
Если направить импульс P противоположно вектору j₀ и сделать его достаточно малым по модулю, то, как легко посчитать в две строчки, средняя по новой волновой функции кинетическая энергия уменьшится на величину e(j₀•P)/m – а значит, уменьшится и полная энергия системы. Но это противоречит предположению о том, что исходная волновая функция ψ была основным состоянием. Ведь любое изменение волновой функции по сравнению с основным состоянием может только увеличить энергию или оставить ее прежней. Отсюда следует, что средний ток в основном состоянии j₀ не может быть отличным от нуля.
Стоит заметить только, что это доказательство вряд ли будет работать, если система заполняет неодносвязную область пространства – например, кольцо. В этом случае из-за периодических граничных условий, налагаемых на волновую функцию при обходе вокруг кольца, мы не можем умножить ψ на exp(iP•Σᵢrᵢ/ℏ) с произвольно малым импульсом P, поскольку он должен квантоваться. Это объясняет наличие незатухающих токов в основном состоянии в небольших кольцах, изготовленных как из нормальных металлов, так и из сверхпроводников, через которые пропущено магнитное поле: теорема Блоха для них неприменима.
Еще большой вопрос, насколько теорема Блоха применима для систем с отсутствующей галилеевой инвариантностью, таких как материалы с бесмассовыми дираковскими и прочими экзотическими электронами. Строго говоря, любые электроны в кристалле не обладают галилеевой инвариантностью, поскольку при вышеописанном построении мы придаем импульс P только электронам, оставляя решетку на месте, так что здесь нужна определенная осмотрительность.
#твердое_тело #сверхпроводимость #объяснения
Physical Review Journals Archive
Note on a Theorem of Bloch Concerning Possible Causes of Superconductivity
Attention is called to a theorem of Bloch, from which it is shown that even when interelectronic interactions are taken into account, the state of lowest electronic free energy corresponds to a zero net current. This result contradicts the hypothesis that…
👍4
Согласно второму началу термодинамики, при взаимодействии двух систем тепло спонтанно перетекает от более горячей к более холодной. В этом эксперименте продемонстрировано обращение теплового потока при наличии квантовых корреляций между системами.
Системы представлены здесь кубитами – ядерными спинами H и ¹³С в молекуле хлороформа. Локально каждый из них находится в тепловом состоянии, но в совместной двухкубитной матрице плотности имеются недиагональные члены α|01><10| + α*|10><01|, отвечающие корреляциям при α ≠ 0. Кубиты приводятся во взаимодействие, сохраняющее их суммарную энергию, при котором они обмениваются теплом.
Графики показывают, как с течением времени меняются энергии изначально более горячего (левый) и холодного (правый) кубитов. В отсутствие корреляций (α = 0) горячий кубит охлаждается, а холодный нагревается. При наличии же корреляций (α = –0.19) тепловой поток меняет свое направление. Хотя при t > 1.1 мс начинается обратная перекачка энергии.
#квантовая_термодинамика
Системы представлены здесь кубитами – ядерными спинами H и ¹³С в молекуле хлороформа. Локально каждый из них находится в тепловом состоянии, но в совместной двухкубитной матрице плотности имеются недиагональные члены α|01><10| + α*|10><01|, отвечающие корреляциям при α ≠ 0. Кубиты приводятся во взаимодействие, сохраняющее их суммарную энергию, при котором они обмениваются теплом.
Графики показывают, как с течением времени меняются энергии изначально более горячего (левый) и холодного (правый) кубитов. В отсутствие корреляций (α = 0) горячий кубит охлаждается, а холодный нагревается. При наличии же корреляций (α = –0.19) тепловой поток меняет свое направление. Хотя при t > 1.1 мс начинается обратная перекачка энергии.
#квантовая_термодинамика
👍2
Кстати говоря, обращенный тепловой поток (из эксперимента из предыдущего поста), текущий от холодной системы к более горячей, нарушает второе начало термодинамики, записанное в локальном виде ΔQ₁/T₁ + ΔQ₂/T₂ ≥ 0. Согласно ему, суммарная энтропия двух систем не может уменьшаться.
Чтобы спасти второе начало термодинамики, нужно рассматривать обе системы как единое целое и учитывать не только тепловую, но и информационную часть энтропии. Из-за этого обобщенное второе начало термодинамики выглядит как ΔQ₁/T₁ + ΔQ₂/T₂ ≥ ΔI₁₂, где ΔI₁₂ – изменение взаимной информации обеих систем. Если сначала они были скоррелированы, а при дальнейшей эволюции корреляции теряются (а именно это и происходит к эксперименте, как показано на графике оранжевыми точками при 0 < t < 1.1 мс), то ΔI₁₂ < 0 и возможны процессы с ΔQ₁/T₁ + ΔQ₂/T₂ < 0.
При таких процессах сумма двух локальных энтропий каждой из систем уменьшается, но энтропия их совокупности, посчитанная с учетом корреляций между ними, увеличивается.
#квантовая_термодинамика
Чтобы спасти второе начало термодинамики, нужно рассматривать обе системы как единое целое и учитывать не только тепловую, но и информационную часть энтропии. Из-за этого обобщенное второе начало термодинамики выглядит как ΔQ₁/T₁ + ΔQ₂/T₂ ≥ ΔI₁₂, где ΔI₁₂ – изменение взаимной информации обеих систем. Если сначала они были скоррелированы, а при дальнейшей эволюции корреляции теряются (а именно это и происходит к эксперименте, как показано на графике оранжевыми точками при 0 < t < 1.1 мс), то ΔI₁₂ < 0 и возможны процессы с ΔQ₁/T₁ + ΔQ₂/T₂ < 0.
При таких процессах сумма двух локальных энтропий каждой из систем уменьшается, но энтропия их совокупности, посчитанная с учетом корреляций между ними, увеличивается.
#квантовая_термодинамика
❤1
p-битами называют вероятностные (probabilistic) биты, которые быстро флуктуируют между состояниями 0 и 1. Их можно считать классическими аналогами кубитов, находящимися в классической статистической смеси двух состояний. С практической точки зрения, наборы p-битов можно использовать для вероятностных вычислений или для быстрого перебора огромного числа вариантов решения комбинаторных задач.
В этой работе описывается миниатюрная реализация p-битов на основе магнитных туннельных переходов, совмещенных с полевыми транзисторами на основе двумерного MoS₂. Магнитный туннельный переход – это два слоя ферромагнетика, между которыми электроны туннелируют, встречая большое сопротивление при антипараллельных направлениях их намагниченностей и меньшее – при параллельных. Если сделать один из ферромагнетиков достаточно малым, он будет быстро перемагничиваться за счет тепловых флуктуаций, так что сопротивление перехода будет флуктуировать. Транзистор используется для усиления флуктуаций сопротивления.
#оптимизация
В этой работе описывается миниатюрная реализация p-битов на основе магнитных туннельных переходов, совмещенных с полевыми транзисторами на основе двумерного MoS₂. Магнитный туннельный переход – это два слоя ферромагнетика, между которыми электроны туннелируют, встречая большое сопротивление при антипараллельных направлениях их намагниченностей и меньшее – при параллельных. Если сделать один из ферромагнетиков достаточно малым, он будет быстро перемагничиваться за счет тепловых флуктуаций, так что сопротивление перехода будет флуктуировать. Транзистор используется для усиления флуктуаций сопротивления.
#оптимизация
👍2
Существует поверье, что в режиме квантового эффекта Холла все токи между контактами переносятся исключительно магнитными краевыми каналами, потому что толща двумерного электронного газа в этом режиме является изолирующей. В этой статье Дэвид Таулес напоминает, что это не так и часть токов может переноситься толщей. Изолирующий характер толщи этому не мешает, поскольку речь идет о холловских токах, а не об обычной, диагональной проводимости.
Как показано на рисунке, если между двумя контактами электрический ток переносится слева направо магнитными краевыми каналами (фиолетовые стрелочки), то один из них – текущий вдоль тока – оказывается более населенным электронами, чем текущий в противоположную сторону. Из-за дисбаланса населенностей краевых каналов возникает электрическое поле (зеленые стрелки), которое, за счет холловской проводимости толщи, дает холловские токи, показанные пунктиром. В типичных условиях через толщу может проходить около 20% суммарного тока.
#уровни_Ландау #объяснения
Как показано на рисунке, если между двумя контактами электрический ток переносится слева направо магнитными краевыми каналами (фиолетовые стрелочки), то один из них – текущий вдоль тока – оказывается более населенным электронами, чем текущий в противоположную сторону. Из-за дисбаланса населенностей краевых каналов возникает электрическое поле (зеленые стрелки), которое, за счет холловской проводимости толщи, дает холловские токи, показанные пунктиром. В типичных условиях через толщу может проходить около 20% суммарного тока.
#уровни_Ландау #объяснения
👍2
В этом эксперименте реализованы аналоговые квантовые вычисления с двумерными массивами до 256 ридберговских атомов, каждый из которых является кубитом.
Как показано на рисунке, в массив оптических пинцетов загружаются атомы, которые затем уплотняются, чтобы не было пропусков. Каждый атом может находиться в суперпозиции основного |g> и ридберговского возбужденного |r> состояний, которые управляемо связываются двухфотонными переходами. Близко расположенные атомы при этом связаны ридберговской блокадой: нахождение одного атома в состоянии |r> сдвигает, за счет взаимодействия Ван-дер-Ваальса, уровни энергии соседних атомов, так что их переходы |g> → |r> выходят из резонанса.
Справа показан пример моделирования антиферромагнитной модели Изинга: ридберговская блокада мешает одновременно возбуждаться ближайшим соседям, так что атомы устанавливаются в состояниях |e> и |g> в шахматном порядке.
#атомные_газы #квантовые_вычисления
Как показано на рисунке, в массив оптических пинцетов загружаются атомы, которые затем уплотняются, чтобы не было пропусков. Каждый атом может находиться в суперпозиции основного |g> и ридберговского возбужденного |r> состояний, которые управляемо связываются двухфотонными переходами. Близко расположенные атомы при этом связаны ридберговской блокадой: нахождение одного атома в состоянии |r> сдвигает, за счет взаимодействия Ван-дер-Ваальса, уровни энергии соседних атомов, так что их переходы |g> → |r> выходят из резонанса.
Справа показан пример моделирования антиферромагнитной модели Изинга: ридберговская блокада мешает одновременно возбуждаться ближайшим соседям, так что атомы устанавливаются в состояниях |e> и |g> в шахматном порядке.
#атомные_газы #квантовые_вычисления
А вот еще интересный пример аналогового квантового моделирования из статьи из предыдущего поста.
Здесь, как показано на панелях (a)-(c), радиус ридберговской блокады постепенно увеличивается (точнее, он остается постоянным, просто сжимается массив атомов). Слева показана наблюдаемая картина люминесценции атомов: находящиеся в состоянии |g> испускают сигнал и видны как зеленые точки, а атомы в состоянии |e> остаются темными (красные круги). Справа показан фурье-образ <F(k)> корреляционной функции плотности.
Сначала ридберговская блокада захватывает лишь ближайших соседей, так что устанавливается «антиферромагнитная» шахматная фаза (a). Затем, когда блокада достигает соседей 2-го порядка по диагонали устанавливается полосатая фаза (b), а при еще большем ее радиусе возникает звездчатая фаза (c). На панелях (d)-(e) показаны экспериментальная и теоретическая фазовые диаграммы, отслеживаемые по пикам <F(k)>, амплитуды которых играют роль параметров порядка.
#атомные_газы #квантовые_вычисления
Здесь, как показано на панелях (a)-(c), радиус ридберговской блокады постепенно увеличивается (точнее, он остается постоянным, просто сжимается массив атомов). Слева показана наблюдаемая картина люминесценции атомов: находящиеся в состоянии |g> испускают сигнал и видны как зеленые точки, а атомы в состоянии |e> остаются темными (красные круги). Справа показан фурье-образ <F(k)> корреляционной функции плотности.
Сначала ридберговская блокада захватывает лишь ближайших соседей, так что устанавливается «антиферромагнитная» шахматная фаза (a). Затем, когда блокада достигает соседей 2-го порядка по диагонали устанавливается полосатая фаза (b), а при еще большем ее радиусе возникает звездчатая фаза (c). На панелях (d)-(e) показаны экспериментальная и теоретическая фазовые диаграммы, отслеживаемые по пикам <F(k)>, амплитуды которых играют роль параметров порядка.
#атомные_газы #квантовые_вычисления
Машина Больцмана – это рекуррентная нейронная сеть, у которой сигнал снимается только с части нейронов, называемых видимыми. Остальные нейроны являются скрытыми, а сигналы на всех нейронах бинарны (±1) и генерируются их вероятностной активацией. В ограниченных машинах Больцмана (RBM) соединения имеются только между видимыми и скрытыми нейронами.
Обученная машина Больцмана генерирует некоторую статистику многомерных векторов сигналов на видимых нейронах x. Распределение таких векторов легко записать аналитически (см. формулу на рисунке): это просто общее распределение состояний видимых x и скрытых h нейронов, просуммированное по состояниям последних.
Но легко записать – это еще не значит легко посчитать. Авторы этой работы доказывают, что задача имитации работы RBM на классическом компьютере является экспоненциально трудной. А именно, трудно как оценить вероятность выпадения любого заданного вектора x, так и генерировать векторы x с приближенной статистикой, близкой к оригинальной.
#нейронные_сети
Обученная машина Больцмана генерирует некоторую статистику многомерных векторов сигналов на видимых нейронах x. Распределение таких векторов легко записать аналитически (см. формулу на рисунке): это просто общее распределение состояний видимых x и скрытых h нейронов, просуммированное по состояниям последних.
Но легко записать – это еще не значит легко посчитать. Авторы этой работы доказывают, что задача имитации работы RBM на классическом компьютере является экспоненциально трудной. А именно, трудно как оценить вероятность выпадения любого заданного вектора x, так и генерировать векторы x с приближенной статистикой, близкой к оригинальной.
#нейронные_сети
Красивый эксперимент с наблюдением сильной связи магнонов в шариках железо-иттриевого граната с электромагнитными модами микроволнового резонатора.
Резонатор представляет собой металлический цилиндр с двумя столбиками внутри, немного не доходящими до верха. В такой структуре, называемой возвратной полостью, возникают две моды, показанные на рисунке. У темной моды (слева) магнитные поля, создаваемые вертикальными токами в столбиках, почти компенсируют друг друга в месте расположения ферромагнитного шарика. У светлой моды магнитные поля от столбиков складываются в центре полости.
На диаграмме снизу показано поляритонное расщепление линий поглощения как функция магнитного поля, позволяющего регулировать резонансную частоту магнонов. Магнонная мода M1, отвечающая однородной по шарику намагниченности, связывается со светлой модой резонатора (21 ГГц), но не с темной (14 ГГц). С темной же модой связываются (хоть и слабо) магнонные моды M2, M3 с неоднородными распределениями намагниченности.
#поляритоны #магнетизм
Резонатор представляет собой металлический цилиндр с двумя столбиками внутри, немного не доходящими до верха. В такой структуре, называемой возвратной полостью, возникают две моды, показанные на рисунке. У темной моды (слева) магнитные поля, создаваемые вертикальными токами в столбиках, почти компенсируют друг друга в месте расположения ферромагнитного шарика. У светлой моды магнитные поля от столбиков складываются в центре полости.
На диаграмме снизу показано поляритонное расщепление линий поглощения как функция магнитного поля, позволяющего регулировать резонансную частоту магнонов. Магнонная мода M1, отвечающая однородной по шарику намагниченности, связывается со светлой модой резонатора (21 ГГц), но не с темной (14 ГГц). С темной же модой связываются (хоть и слабо) магнонные моды M2, M3 с неоднородными распределениями намагниченности.
#поляритоны #магнетизм
👍2
Вот красивая идея использования неравновесной системы в качестве демона Максвелла, позволяющего превращать тепло в работу или перекачивать тепло от холодного резервуара к горячему. В отличие от обычного демона Максвелла, проводящего над системой измерения и затем осуществляющего обратную связь, здесь неравновесная система ничего такого не делает, поэтому авторы называют ее N-демоном.
Идея показана на рисунке сверху: N-демон запускает в рабочее тело неравновесно распределенные частицы – отдельно «холодные» и «горячие» (синие и красные), забирая обратно равновесно распределенные (фиолетовые). Если суммарные потоки числа частиц и энергии между рабочим телом и N-демоном равны нулю, то последний является лишь поставщиком «неравновесности» – точнее, негэнтропии.
Глобально второе начало термодинамики здесь не нарушается, поскольку положительное производство энтропии внутри N-демона перекрывает ее отрицательное производство в рабочем теле и связанных с ним резервуарах.
#стохастическая_термодинамика
Идея показана на рисунке сверху: N-демон запускает в рабочее тело неравновесно распределенные частицы – отдельно «холодные» и «горячие» (синие и красные), забирая обратно равновесно распределенные (фиолетовые). Если суммарные потоки числа частиц и энергии между рабочим телом и N-демоном равны нулю, то последний является лишь поставщиком «неравновесности» – точнее, негэнтропии.
Глобально второе начало термодинамики здесь не нарушается, поскольку положительное производство энтропии внутри N-демона перекрывает ее отрицательное производство в рабочем теле и связанных с ним резервуарах.
#стохастическая_термодинамика
А вот варианты реализации N-демона, предлагаемые авторами стати из предыдущего поста и позволяющие понять, как в принципе эта штука может работать.
Слева показана электронная реализация, основанная на двумерном электронном газе с магнитными краевыми каналами, присоединенным к четырем контактам. Верхняя часть системы представляет собой N-демона. Его назначение – запускать в нижнюю часть (рабочее тело) существенно неравновесное распределение электронов по энергии f_N(E), отличающееся от распределения Ферми-Дирака. Это достигается наложением «горячего» распределения Ферми-Дирака (электронов, идущих от красного контакта) и «холодного» распределения (от синего контакта), пропускаемых через туннельный переход с коэффициентом пропускания T_d(E), существенно зависящим от энергий.
Справа показана фотонная реализация, где, для аналогичных целей, используются полупрозрачные зеркала с коэффициентом пропускания, существенно зависящим от длины волны.
#стохастическая_термодинамика
Слева показана электронная реализация, основанная на двумерном электронном газе с магнитными краевыми каналами, присоединенным к четырем контактам. Верхняя часть системы представляет собой N-демона. Его назначение – запускать в нижнюю часть (рабочее тело) существенно неравновесное распределение электронов по энергии f_N(E), отличающееся от распределения Ферми-Дирака. Это достигается наложением «горячего» распределения Ферми-Дирака (электронов, идущих от красного контакта) и «холодного» распределения (от синего контакта), пропускаемых через туннельный переход с коэффициентом пропускания T_d(E), существенно зависящим от энергий.
Справа показана фотонная реализация, где, для аналогичных целей, используются полупрозрачные зеркала с коэффициентом пропускания, существенно зависящим от длины волны.
#стохастическая_термодинамика
Электрон, падающий из нормального металла на границу со сверхпроводником, претерпевает андреевское отражение, если его энергия лежит внутри щели. При этом после поглощении электрона сверхпроводником из последнего вылетает дырка. Андреевское отражение является не зеркальным (specular reflection), а обратным (retroreflection): траектория дырки повторяет траекторию электрона в обратном порядке.
В этой работе теоретически рассмотрен аналог андреевского отражения от бозе-конденсата экситонных поляритонов, в спектре возбуждений которых из-за резонансной накачки имеется щель.
На панели (a) показаны режимы отражения в зависимости от энергии поляритона E, падающего из нормальной области на бозе-конденсированную, и от угла падения θ_I. Возможны режимы отражения частицы без пропускания (b), отражения с пропусканием (d) или полного перехода частицы в распространяющуюся вдоль границы эванесцентную волну без отражения и без пропускания (c).
#поляритоны #бозе_конденсация #сверхпроводимость
В этой работе теоретически рассмотрен аналог андреевского отражения от бозе-конденсата экситонных поляритонов, в спектре возбуждений которых из-за резонансной накачки имеется щель.
На панели (a) показаны режимы отражения в зависимости от энергии поляритона E, падающего из нормальной области на бозе-конденсированную, и от угла падения θ_I. Возможны режимы отражения частицы без пропускания (b), отражения с пропусканием (d) или полного перехода частицы в распространяющуюся вдоль границы эванесцентную волну без отражения и без пропускания (c).
#поляритоны #бозе_конденсация #сверхпроводимость
Вот это крутой эксперимент, в котором наглядно продемонстрированы сверхнизкие значения скорости Ферми в почти плоских зонах двухслойного графена, повернутого на «магический угол», а также необычный характер его сверхпроводимости.
Графики сверху показывают зависимости дифференциальной проводимости от тока, измеренные при различных уровнях допирования ñ. Пики дифференциальной проводимости в нормальном состоянии, при подавлении сверхпроводимости магнитным полем (синие кривые), возникают, когда скорость электронов, переносящих ток J, сравнивается со скоростью Ферми v_F. Измеренные таким образом значения v_F могут доходить до рекордно низких 700 м/с.
В сверхпроводящей фазе (красные кривые) возникают дополнительные пики при критическом токе J_c сверхпроводника. Как демонстрируется на графике снизу, при малых |ñ| критический ток J_c связан с ограничением скорости электронов величиной v_F, а при больших |ñ| – обычным для сверхпроводников условием развала куперовских пар v = Δ/(ħ×k_F).
#сверхпроводимость #графен
Графики сверху показывают зависимости дифференциальной проводимости от тока, измеренные при различных уровнях допирования ñ. Пики дифференциальной проводимости в нормальном состоянии, при подавлении сверхпроводимости магнитным полем (синие кривые), возникают, когда скорость электронов, переносящих ток J, сравнивается со скоростью Ферми v_F. Измеренные таким образом значения v_F могут доходить до рекордно низких 700 м/с.
В сверхпроводящей фазе (красные кривые) возникают дополнительные пики при критическом токе J_c сверхпроводника. Как демонстрируется на графике снизу, при малых |ñ| критический ток J_c связан с ограничением скорости электронов величиной v_F, а при больших |ñ| – обычным для сверхпроводников условием развала куперовских пар v = Δ/(ħ×k_F).
#сверхпроводимость #графен
А вот еще интересные особенности сверхпроводимости в двухслойном графене, повернутом на «магический угол».
Во-первых, отношение Δ(0)/T_c щели при T = 0 к критической температуре здесь составляет около 0.05 – вместо даваемого теорией БКШ отношения 1.75, типичного для обычных сверхпроводников. Это свидетельствует о необычном характере сверхпроводимости.
Во-вторых, отношение T_c/T_F критической температуры к энергии Ферми T_F здесь больше 1 и может достигать аж 9 (красная кривая на графике слева), в то время как при спаривании в режиме слабой связи оно должно быть много меньше 1. А для электронов с квадратичной дисперсией оно, независимо от механизма спаривания, не может превышать 1/8.
В-третьих, измеренная разными способами сверхтекучая плотность (зеленая и красная кривые на графике справа) во много раз превышает даваемую формулой Ландау (черный пунктир). Это наглядная демонстрация геометрического вклада в сверхтекучую плотность, не учитываемого формулой Ландау.
#сверхпроводимость #графен
Во-первых, отношение Δ(0)/T_c щели при T = 0 к критической температуре здесь составляет около 0.05 – вместо даваемого теорией БКШ отношения 1.75, типичного для обычных сверхпроводников. Это свидетельствует о необычном характере сверхпроводимости.
Во-вторых, отношение T_c/T_F критической температуры к энергии Ферми T_F здесь больше 1 и может достигать аж 9 (красная кривая на графике слева), в то время как при спаривании в режиме слабой связи оно должно быть много меньше 1. А для электронов с квадратичной дисперсией оно, независимо от механизма спаривания, не может превышать 1/8.
В-третьих, измеренная разными способами сверхтекучая плотность (зеленая и красная кривые на графике справа) во много раз превышает даваемую формулой Ландау (черный пунктир). Это наглядная демонстрация геометрического вклада в сверхтекучую плотность, не учитываемого формулой Ландау.
#сверхпроводимость #графен
Использование чат-ботов наподобие ChatGPT для генерации справочных данных о свойствах и перспективах химических соединений наталкивается на проблему: в литературе, используемой для их обучения, имеется перекос в сторону небольшого числа «хайповых» тем.
В то же время, в научных базах данных (
Авторы этой работы сделали попытку исправить этот перекос, обучив на научных базах данных графовую нейронную сеть, а затем на основе этого (я не понял, как именно) заставив ChatGPT-3.5-turbo генерировать текстовые описания материалов. ChatGPT-4 и эксперты-люди достаточно высоко оценили эти тексты по критериям фактической точности, глубины содержания и правильности языковой структуры.
#нейронные_сети #популярное
В то же время, в научных базах данных (
OQMD, Materials Project, JARVIS, COD, AFLOW2) пространство соединений покрывается более равномерно. Для примера можно посмотреть (сверху на рисунке) на частоты встречаемости химических элементов в обоих случаях. В первом случае наблюдается перекос в сторону оксидов, органики и соединений меди и железа.Авторы этой работы сделали попытку исправить этот перекос, обучив на научных базах данных графовую нейронную сеть, а затем на основе этого (я не понял, как именно) заставив ChatGPT-3.5-turbo генерировать текстовые описания материалов. ChatGPT-4 и эксперты-люди достаточно высоко оценили эти тексты по критериям фактической точности, глубины содержания и правильности языковой структуры.
#нейронные_сети #популярное
Вязкость жидкости η связана с ее способностью к поперечному переносу импульса. Она пропорциональна времени свободного пробега τ квазичастиц, поэтому при низких температурах в ферми-жидкости, когда τ ~ T⁻², вязкость в норме также растет как η ~ T⁻². Но при наличии фазовых переходов на фоне этой зависимости могут возникать особенности.
В этом эксперименте впервые наблюдалось предсказанное почти 50 лет назад резкое уменьшение вязкости жидкого ³He вблизи перехода в сверхтекучее состояние, обусловленное флуктуациями куперовских пар. Вязкость оценивалась как η ~ Q⁻² по сверхчувствительным измерениям добротности Q колебаний кварцевого резонатора в форме вилки, погруженного в ³He. Как видно на графиках для различных давлений, вблизи сверхтекучего перехода рассеяние квазичастиц на флуктуациях куперовских пар резко снижает τ и, как следствие, понижает η и увеличивает Q. Резкий рост добротности Q накладывается на ее обычное фермижидкостное поведение Q ~ T.
#гидродинамика #сверхпроводимость #сверхтекучесть
В этом эксперименте впервые наблюдалось предсказанное почти 50 лет назад резкое уменьшение вязкости жидкого ³He вблизи перехода в сверхтекучее состояние, обусловленное флуктуациями куперовских пар. Вязкость оценивалась как η ~ Q⁻² по сверхчувствительным измерениям добротности Q колебаний кварцевого резонатора в форме вилки, погруженного в ³He. Как видно на графиках для различных давлений, вблизи сверхтекучего перехода рассеяние квазичастиц на флуктуациях куперовских пар резко снижает τ и, как следствие, понижает η и увеличивает Q. Резкий рост добротности Q накладывается на ее обычное фермижидкостное поведение Q ~ T.
#гидродинамика #сверхпроводимость #сверхтекучесть
В этой работе была выведена обобщенная теорема Гельмана-Фейнмана, связывающая малые изменения энергий стационарных состояний с изменениями гамильтониана, для неэрмитовых PT-симметричных систем.
Авторы демонстрируют, что и в PT-симметричной фазе, и в фазе с нарушенной PT-симметрией она имеет один и тот же вид, показанный на рисунке. Здесь |R> и |L> – правые и левые собственные векторы гамильтониана, G – оператор, превращающий правые векторы в левые.
На графиках показан пример сравнения модулей левой и правой частей теоремы, посчитанных для нескольких стационарных состояний двумерного ангармонического осциллятора с неэрмитовой добавкой к гамильтониану iλxy. При λ = 4 имеется исключительная точка, в которой для некоторых состояний производная ∂E/∂λ расходится. Тем не менее, обобщенная теорема Гельмана-Фейнмана всегда продолжает выполняться. Расходимость ∂E/∂λ свидетельствует о высокой чувствительности системы к малым изменениям λ, что само по себе интересно.
#квантовая_механика #неэрмитовы_системы
Авторы демонстрируют, что и в PT-симметричной фазе, и в фазе с нарушенной PT-симметрией она имеет один и тот же вид, показанный на рисунке. Здесь |R> и |L> – правые и левые собственные векторы гамильтониана, G – оператор, превращающий правые векторы в левые.
На графиках показан пример сравнения модулей левой и правой частей теоремы, посчитанных для нескольких стационарных состояний двумерного ангармонического осциллятора с неэрмитовой добавкой к гамильтониану iλxy. При λ = 4 имеется исключительная точка, в которой для некоторых состояний производная ∂E/∂λ расходится. Тем не менее, обобщенная теорема Гельмана-Фейнмана всегда продолжает выполняться. Расходимость ∂E/∂λ свидетельствует о высокой чувствительности системы к малым изменениям λ, что само по себе интересно.
#квантовая_механика #неэрмитовы_системы