Познавательная статья, дающая педагогическое введение в тему квантового броуновского движения. Это движение частицы, взаимодействующей с термостатом – как правило, набором большого числа независимых гармонических осцилляторов.

Сначала авторы подробно описывают классическое броуновское движение, показывая, как из связанных уравнений динамики самой частицы и частиц термостата можно исключить термостат, получив – при некоторых допущениях – уравнение Ланжевена. Роль термостата сводится к воздействию на частицу двух сил: силы трения и случайной силы, отвечающей за тепловое движение. Важный момент здесь – флуктуационно-диссипационная теорема, связывающая между собой величину трения, интенсивность случайной силы и температуру термостата.

Затем описывается уже квантовое броуновское движение. Здесь все похоже, только воздействие термостата выражается уже операторами. А еще из-за бозе-статистики осцилляторов термостата во многих выражениях, характеризующих его воздействие на частоте ω, появляются множители вида cth(ω/2T). Авторы отдельно обсуждают квантовую теорему о равнораспределении энергии по степеням свободы, которая, из-за комбинации квантовых эффектов и диссипации, имеет не совсем тривиальный вид.

Еще одна любопытная штука – диссипативный диамагнетизм, возникающий при двумерном квантовом броуновском движении в магнитном поле. Взаимодействие заряженной частицы с термостатом приводит к дополнительному вкладу в ее магнитный отклик. Полезно и то, что в статье проводятся связи между квантовым броуновским движением и современными темами, такими как стохастическая термодинамика и флуктуационные теоремы.

#объяснения #открытые_квантовые_системы

Красивая экспериментальная работа, в которой был реализован топологический изолятор Андерсона – материал, который становится топологически нетривиальным лишь под влиянием достаточно сильного беспорядка. Это одна из первых реализаций материалов такого класса.

https://telegra.ph/Topologicheskij-izolyator-Andersona-dlya-fotonov-07-03

#топологические_материалы #фотоника

Работа из разряда «техника на грани фантастики»: автономная лаборатория «Ада», которая самостоятельно занимается поиском оптимальных технологических процессов синтеза материалов. Лаборатория состоит из компьютерной системы и роботизированной платформы, способной подбирать реагенты, изготавливать образцы материала и исследовать их свойства. На один образец у нее уходит 20-30 минут, нужно только поставлять ей расходники.

В предыдущей работе эта лаборатория училась создавать тонкие пленки органического полупроводника с дырочной проводимостью. Ее целью было добиться наибольшей подвижности дырок при варьировании степени допирования материала и времени его отжига. Меньше чем за сутки она полностью без вмешательства человека нашла оптимальные условия, повысив исходную подвижность дырок на 1-2 порядка.

Здесь «Ада» подбирала условия изготовления тонких проводящих пленок палладия на полимерной подложке. Ее целью было определить парето-фронт: кривую в пространстве свойств материала – в данном случае проводимости пленки и температуры отжига, – показывающую достижимый на практике компромисс между ними (чем больше нужна проводимость пленки, тем более высокой должна быть температура).

Ей удалось найти не только оптимальные технологии процессов для уже известных раньше пленок, изготавливаемых при температуре 250 °C, но и открыть новые методы, требующие более низкой температуры 190 °C и расширяющие диапазон полимеров, которые можно использовать в качестве подложки.

Особая ценность таких автономных лабораторий в том, что они могут довольно быстро и эффективно проводить поиск в многомерном пространстве параметров, характеризующих технологический процесс (концентрации легирующих примесей, температуры и длительности отжига, времена напыления и т.д.). Человеку же довольно тяжело ориентироваться в пространствах таких размерностей, удерживая в голове множество факторов одновременно.

Результат получается почти как в компьютерной игре, когда ты нажимаешь исследовать апгрейд брони своих юнитов, и через некоторое время получаешь технологию «броня +1» без необходимости самому заниматься материаловедением и лабораторными экспериментами.

#популярное #отвал_башки

Достаточно очевидно, что турбулентность, со своей фрактальной структурой потоков и завихрений, должна демонстрировать масштабную инвариантность, то есть выглядеть одинаково при равномерном растяжении или сжатии системы. Конформная же инвариантность – это более сильное свойство, состоящее в неизменности статистических свойств при неравномерных растяжениях или сжатиях, сохраняющих углы. Такое свойство двумерной турбулентности было проверено в экспериментах.

https://telegra.ph/Poznavatelnaya-statya-dayushchaya-pedagogicheskoe-vvedenie-v-temu-kvantovogo-brounovskogo-dvizheniya-EHto-dvizhenie-chasticy-vza-07-03

#гидродинамика #фракталы

А вот недавняя работа, тоже посвященная конформной инвариантности двумерного турбулентного движения, но не обычного, а сверхтекучего. Здесь был проведен эксперимент с бозе-конденсатом экситонных поляритонов.

Особенность сверхтекучей турбулентности в том, что она завязана на дискретные единицы – квантованные вихри, из-за чего ее масштабная инвариантность слегка нарушается. Тем не менее, на масштабах длины залечивания конденсата картина завихренности, показанная слева, демонстрирует все свойства, характерные для конформной инвариантности – в том числе, степенное распределение размеров с показателем 96/91. Графики же справа демонстрируют масштабную инвариантность на больших расстояниях: статистическое распределение циркуляций скорости, посчитанных вдоль квадратных петель различных размеров R (превышающих длину залечивания 2.3 мкм), ложится на одну и ту же кривую. Причем кривая эта степенная, а не гауссова – что тоже свидетельствует об отсутствии характерного масштаба.

#гидродинамика #сверхтекучесть #поляритоны

Полезная диаграмма из небольшого обзора по сверхбыстрой динамике электронов, дырок и экситонов в гетероструктурах двумерных дихалькогенидов переходных металлов. На этой диаграмме для каждого материала показано расположение валентной зоны и зоны проводимости, найденное при помощи функционала плотности PBE (синие полоски) и метода GoWo (розовые полоски). Поскольку функционал плотности часто ошибается насчет щели в полупроводниках, розовые полоски дают более надежные результаты.

Из этой диаграммы видно, что при контакте практически любой пары материалов возникает выравнивание зон II-го типа: когда в общую энергетическую щель частично залазит валентная зона одного материала и зона проводимости другого материала. В таком случае низшим по энергии возбуждением будет межслойный экситон.

#дихалькогениды_переходных_металлов #экситоны

Любопытная работа, в которой не только описывается простая модель биологического видообразования, но и проводятся интересные физические параллели: разделение популяции на отдельные виды во многом похоже на нарушение симметрии реплик в спиновом стекле – застревании системы в одном из бассейнов эргодичности.

https://telegra.ph/Vidoobrazovanie-v-modeli-spinovogo-stekla-07-04

#стекла #биология #фазовые_переходы #популярное

Вот это очень крутая работа фундаментального уровня, устанавливающая взаимосвязь между краевыми модами топологического изолятора и квантовыми состояниями неэрмитовой системы.

Давно было замечено, что магнитные краевые каналы, распространяющиеся лишь в одну сторону вдоль границы двумерной системы (электронного газа в магнитном поле либо модели Холдейна), очень похожи на состояния частиц в неэрмитовой модели Хатано-Нельсона. Это одномерная цепочка с перескоками между соседними узлами, имеющими разные амплитуды в направлениях влево и вправо. Из-за такой асимметрии состояния, движущиеся в одном направлении, экспоненциально усиливаются, а в другом направлении – наоборот, затухают. Если мы рассмотрим динамику на больших временах, когда выживают лишь состояния, движущиеся «по течению», эффективно получается аналог однонаправленной краевой моды.

Авторы этой работы показывают, что такая параллель – не просто случайное совпадение. Краевая мода любого эрмитового (d+1)-мерного топологического изолятора, эквивалентна – в смысле динамики на больших временах – некоторой d-мерной системе с неэрмитовым гамильтонианом. При этом класс симметрии топологического изолятора (один из 10 классов Алтланда-Цирнбауэра) однозначно связан с классом симметрии неэрмитовой системы (одним из 38 классов Бернарда-ЛеКлера). А необычные свойства краевых мод – такие, как невзаимность, безмассовость или киральность – естественным образом воспроизводятся и неэрмитовой моделью, имеющей на единицу меньшую размерность.

#объяснения #топологические_материалы #неэрмитовы_системы

Загадочные каббалистические диаграммы из статьи из предыдущего поста.

То, что чаще всего называют соотношением неопределенностей Гейзенберга, на самом деле является либо соотношением неопределенностей Кеннарда-Вейля, либо соотношением неопределенностей Робертсона-Шредингера. Сам же Гейзенберг сформулировал лишь качественный принцип неопределенности.

Вот табличка, помогающая не запутаться во всех этих неопределенностях.

#объяснения #квантовая_механика

Очередной неупорядоченный топологический изолятор для фотонов, работающий в микроволновой области частот. В отличие от топологического изолятора Андерсона, который, собственно, создается беспорядком, здесь все наоборот – беспорядок пытается разрушить топологически нетривиальную щель.

Реализован фотонный топологический изолятор при помощи треугольной решетки гиромагнитных цилиндров в магнитном поле, зажатой между металлическими пластинами. Беспорядок с величиной DI вносится случайными сдвигами стержней из узлов решетки.

На фазовой диаграмме можно видеть, что при увеличении DI щель в спектре сужается и сдвигается, но держится до DI = 0.45. Это значение не случайно: после него теряется характерный для кристалла ближний порядок, так что система становится больше похожа на «жидкость». Снизу показаны результаты эксперимента, демонстрирующего распространение электромагнитной волны вдоль края по часовой стрелке при DI ≤ 0.45 и потерю этого свойства при DI = 0.8.

#топологические_материалы #фотоника

Занятная формула, которую в этой работе называют «формулой Леггетта», для доли сверхтекучей компоненты бозе-газа в периодическом потенциале (фактически, суперсолида). Энтони Леггеттом было доказано, что эта формула дает верхнюю границу для доли сверхтекучей компоненты в неоднородной системе, где плотность конденсата ρ(x) зависит от координаты. Но если неоднородность носит периодический характер и бозе-газ является слабо взаимодействующим, эта формула дает точное равенство.

Для проверки формулы в эксперименте был создан двумерный бозе-конденсат атомов рубидия в одномерном периодическом потенциале. Плотность сверхтекучего отклика в направлении оси x (где потенциал периодический) может быть определена по скорости звука, и результат показан на графике фиолетовыми точками. Красные же точки показывают результат, даваемый формулой Леггетта на основе экспериментально измеренного профиля ρ(x). Видно, что она хорошо работает при всех амплитудах V₀ периодического потенциала.

#сверхтекучесть #суперсолид #атомные_газы

Мало кто знает, что обычный водяной лед – это, строго говоря, не совсем кристалл. Молекулы воды как целое – в лице своих атомов кислорода – действительно выстроены в нем в алмазоподобную кристаллическую решетку. А вот с атомами водорода дело обстоит сложнее.

Каждый атом водорода должен находиться между двумя соседними атомами кислорода, создавая водородную связь – причем ближе к одному из атомов кислорода, чем к другому. Вместе с тем, для электрической нейтральности возле каждого атома кислорода должны располагаться два атома водорода. Эти условия, называемые ice rules, ограничивают число различных вариантов расположения атомов водорода в кристалле льда.

Тем не менее, число вариантов все равно остается экспоненциально растущим с ростом размера системы. Это пример геометрической фрустрации, то есть наличия экспоненциально большого числа состояний одинаковой энергии. Как впервые показал Лайнус Полинг, она дает постоянный вклад в энтропию льда, не исчезающий даже при нулевой температуре.

#популярное #стекла

В этом эксперименте были продемонстрированы четно-нечетные эффекты спаривания в одномерной системе нескольких атомов-фермионов, подобные эффектам четности в атомных ядрах.

Притягивающиеся друг к другу атомы лития-6 помещались в наклонную ловушку, из которой они могут выскочить путем туннелирования – либо поодиночке, либо сразу куперовскими парами. Измеряя число оставшихся атомов в ловушке как функцию времени и подгоняя его под экспоненциальные законы распада, можно определить энергию ионизации, высвобождающуюся при вылете одного атома.

На графике видно, что энергия ионизации резко меняется вверх-вниз при переходе от четного числа атомов (с полным соединением в куперовские пары) к нечетному числу (где остается один неспаренный атом). При этом можно видеть даже то, как энергия спаривания двух атомов зависит от номера «оболочки», на которой оно происходит.

#квантовая_механика #сверхпроводимость

Классическая статья Латинджера, в которой он предложил квантовомеханический метод расчета коэффициента теплопроводности и подобных ему величин, связанных с потоками тепла. Этот метод, использующий аналогию с общей теорией относительности, стал впоследствии общепринятым.

Для понимания этого метода можно отправиться от обычной формулы Кубо – или теории линейного отклика – для расчета электрической проводимости. Эта формула подразумевает, что гамильтониан системы возмущается на величину ρ(r)φ(r), где ρ(r) – оператор плотности заряда системы, φ(r) – потенциал внешнего электрического поля. Как линейный отклик на это возмущение, мы считаем электрический ток, получая проводимость.

Если же мы хотим найти отклик системы на локальный нагрев, можно добавить к гамильтониану величину h(r)ψ(r), где h(r) – оператор плотности энергии (или плотности гамильтониана), ψ(r) – некий эффективный потенциал, похожий на внешний гравитационный потенциал со знаком минус. Считая линейный отклик электрического тока на это возмущение, мы рассматриваем термоэлектрический эффект, а считая отклик потока энергии, мы находим теплопроводность. Таким образом, коэффициент теплопроводности можно считать также по формуле Кубо, как отклик потока энергии на плотность энергии h(r).

Добавку к гамильтониану h(r)ψ(r) можно объяснить еще и таким способом: если наша система находится в тепловом равновесии с матрицей плотности ~exp(–H/T), то локальные вариации температуры ΔT(r), как видно из этого выражения, математически эквивалентны локальным вариациям гамильтониана ΔH(r), то есть локальному масштабированию гамильтониана в большую или меньшую стороны, которое как раз и производится добавкой h(r)ψ(r).

Более позднее изобретение, основанное на этом методе и позволяющее рассчитывать теплопроводность при численном моделировании квантовой системы, следующее: на одной из границ системы на волновую функцию мы накладываем граничное условие, заставляющее вращаться ее фазу равномерно с течением времени, как θ = –ΔEt/ℏ. Такое условие эквивалентно локальному увеличению энергии на величину ΔE, запускающему с этой границы через всю систему тепловой поток.

https://journals.aps.org/pr/abstract/10.1103/PhysRev.135.A1505

#квантовая_механика

А вот как Латинджер объясняет, почему он использует представление о действующем на систему гравитационном поле для расчета ее теплопроводности.

Насчет последней фразы: мне тоже приходила в голову такая мысль, что, если бы некие инопланетяне разрабатывали квантовую механику, ничего не зная об электромагнетизме, то они могли бы догадаться о его существовании просто исходя из соображений калибровочной инвариантности.

Действительно, если мы допускаем, что можем отмерять фазу волновой функции от точек отсчета на окружности от 0 до 2π, произвольно зависящих от координат и времени (то есть осуществлять локальные калибровочные преобразования), это автоматически влечет необходимость включения в гамильтониан контрчленов – скалярного и векторного потенциалов электромагнитного поля. Они компенсируют возникающие из-за калибровочных преобразований нефизичные добавки к производным волновой функции.

#цитаты

Красивая картинка с очень четким поляритонным расщеплением в терагерцовой области.

Поляритоны в этой работе даются гибридизацией электромагнитной моды в резонаторе и перехода между соседними уровнями Ландау в двумерном электронном газе в магнитном поле.

Изменение магнитного поля меняет энергию перехода между уровнями Ландау и, тем самым, позволяет управлять расстройкой поляритонного резонанса. Из-за правил отбора этого перехода поляритоны циркулярно поляризованы, а поскольку через структуру пропускают линейно поляризованный свет, на спектрах видна комбинация двух поляритонов одной циркулярной поляризации и нетронутой моды резонатора противоположной поляризации.

#поляритоны #уровни_Ландау

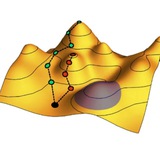
Заковыристый математический анализ критических точек – минимумов, максимумов и седловых точек – многомерного ландшафта, образуемого случайным потенциалом с гауссовыми корреляциями.

Такой анализ позволяет понять общие черты поведения хаотично устроенных случайных ландшафтов в пространствах очень высокой размерности. Подобные ландшафты возникают при обучении нейросетей (ландшафт функции ошибок), в теории стекол и прочих сложных систем (ландшафты энергии, свободной энергии и прочих величин).

Результаты, в принципе, получаются интуитивно понятными. На дне энергетического спектра почти все критические точки – локальные минимумы, на потолке – почти одни локальные максимумы. В середине же все заполнено седловыми точками.

#стекла

Вот это настоящий топологический изолятор для фотонов: в отличие от многочисленных «фотонных метаматериалов», работающих в микроволновой области спектра, где о фотонах можно говорить весьма условно, эта штука работает уже в видимой области, в районе 700 нм.

Двумерная решетка этого фотонного кристалла состоит из кремниевых нанопризм диаметром 250 нм. Подобно тому, как зонная структура обычного кристалла строится на электронных орбиталях отдельных атомов, здесь основой являются резонансы Ми в диэлектрических призмах. Некоторые из них с хорошим пространственным разрешением показаны на картинке.

Я обратил внимание на необычный метод детектирования фотонных состояний в такой структуре. Она облучалась электронами энергией 30 кэВ, которые, попадая в кремний, вызывают катодолюминесценцию – испускание вторичных электромагнитных волн с широким спектром. Те из них, что попадают энергией в фотонные блоховские состояния, излучаются с характерной для них пространственной структурой.

#топологические_изоляторы #фотоника

Действительно, Такахиро Сагава все по фактам разложил.

https://arxiv.org/abs/1202.0983

#цитаты

Бомбическая статья, где была изобретена «квантовая смазка» – способ повысить эффективность теплового двигателя, подавив в нем вредные квантовые эффекты.

Здесь рассматривается двухкубитный двигатель, работающий согласно циклу Отто: акты расширения и сжатия чередуются с актами нагревания и охлаждения. Полезная работа извлекается за счет того, что нагретая система расширяется с большей силой, а охлажденная система, наоборот, легче сжимается. В ходе работы двигателя генерируются квантовые когерентности – недиагональные элементы матрицы плотности. На их генерацию тратится дополнительная энергия, так что формирование когерентностей ухудшает характеристики двигателя.

Квантовая смазка – это внешний фактор, вызывающий дополнительную декогеренцию и быстро подавляющий недиагональные элементы. Как видно на графике справа, с ростом интенсивности смазывания Λ увеличивается мощность двигателя (красная кривая) и снижается производство энтропии, то есть диссипация (синяя кривая).

#квантовая_термодинамика #отвал_башки