Среди двумерных дихалькогенидов переходных металлов есть материалы с весьма интересными свойствами: анизотропные, топологически нетривальные, экситонные диэлектрики и т.д. В этой работе показано, что допированный молибденом двумерный кристалл WTe₂ обладает анизотропным оптическим откликом и гиперболичностью в некоторой полосе частот.

На графиках показаны результаты измерений коэффициента поглощения (левый столбец графиков) и извлеченные из них частотные зависимости Im σ (правый столбец) для двух направлений линейной поляризации. Три строки диаграмм отвечают разным уровням допирования молибденом x. Серым цветом показаны области гиперболичности, где Im σ в двух направлениях имеют разные знаки – она находится в дальнем инфракрасном диапазоне.

В эксперименте авторы каким-то запутанным образом подтверждают существование гиперболических плазмонов, изготавливая из материала массивы нанолент, вырезанных под разными углами, и измеряя их спектры поглощения.

#дихалькогениды_переходных_металлов

Недавно я писал о квантовых батареях – устройствах хранения энергии, использующих квантовые эффекты для увеличения скорости ее накопления или отдачи. А вот работа, в которой исследовались фундаментальные пределы для скорости таких процессов.

Авторы показывают, что скорость P обмена энергией между квантовой батареей и окружением (то есть скорость зарядки или разрядки) ограничена неравенством P ≤ ΔH×√I_E, где ΔH – разброс энергий батареи, I_E – фишеровская информация, определяющая, насколько быстро статистическое распределение энергий батареи меняется с течением времени.

При этом I_E ≤ I_Q, где I_Q – квантовая фишеровская информация, показывающая, насколько быстро с течением времени изменяется матрица плотности батареи. Действительно, как показано на рисунке, в пространстве квантовых состояний (сверху) система может двигаться быстрее, чем в пространстве распределений энергии (снизу). С точки зрения эффективности батареи, это излишний расход ресурсов, потому что важна только I_E.

#квантовая_термодинамика

А вот пример того, как работает квантовое преимущество при зарядке квантовой батареи. Здесь рассматривается простейшая модель батареи в виде набора невзаимодействующих кубитов с гамильтонианом H_B. Квантовость системы вступает в игру в процессе ее зарядки, через гамильтониан взаимодействия H_C батареи с окружающей средой.

Первый вариант такого гамильтониана, показанный на рисунке слева, отвечает параллельной зарядке: каждый кубит перекачивается из основного состояния в возбужденное через действующий на него оператор σ_x. Второй вариант (справа) отвечает глобальной зарядке: это тензорное произведение всех операторов σ_x, а не их сумма.

Диаграммы показывают, как с течением времени меняется распределение энергий батареи. В случае параллельной зарядки батарея последовательно взбирается вверх по энергии, от каждого многочастичного уровня энергии к соседнему. При глобальной же зарядке система сразу переходит из основного состояния в наивысшее возбужденное, минуя промежуточные стадии.

#квантовая_термодинамика

«Осью зла» в астрофизике называют направление на небесной сфере, в котором приходящее к нам реликтовое излучение обладает в повышенной температурой. Это направление, в терминах углов прямого восхождения α и склонения δ, составляет примерно (α, δ) ≈ (173º, 4º).

Наличие такой анизотропии реликтового излучения может свидетельствовать о том, что наша Солнечная система, да и вся Галактика тоже, движутся по отношению к остальной Вселенной. Такое обстоятельство противоречит принципу Коперника – предположению о том, что наше положение во Вселенной ничем не выделено.

В этой работе было показано, что излучение квазаров также анизотропно: оно демонстрирует максимальное синее смещение вблизи (α, δ) ≈ (190º, 0º), как показано синим цветом на диаграмме. Это может говорить о движении нашей Галактики со скоростью 50000 км/с, в этом направлении, весьма близком к «оси зла».

Впрочем, последующие исследования не подтвердили наличия «оси зла» в реликтовом излучении, так что вопрос остается открытым...

#популярное #астрофизика

Топологические изоляторы Черна демонстрируют квантование удельной холловской проводимости, частным случаем чего является квантовый эффект Холла. В этой работе показано, что квантуется еще одна величина – циркулярный дихроизм скорости межзонных переходов.

Как показано на рисунке, под действием право- или левополяризованной раскачки частиц внешней силой с амплитудой E и частотой ω происходят межзонные переходы со скоростями Γ₊ и Γ₋ в расчете на единицу площади. Интеграл их разности ΔΓ = Γ₊–Γ₋ по всем частотам, деленный на квадрат амплитуды поля E², равен числу Черна заполненной энергетической зоны, из которой происходят межзонные переходы.

Снизу показано, почему так происходит: дихроизм ΔΓ скорости межзонных переходов, посчитанный по золотому правилу Ферми, дается таким же выражением, как число Черна ν и пропорциональная ему удельная холловская проводимость. Кстати говоря, предсказанное квантование впоследствии было подтверждено в эксперименте с атомным газом в оптической решетке.

#топологические_материалы

Квантованными полувихрями в спинорном бозе-конденсате называются топологические возбуждения, при которых вихрь возникает только в одной компоненте (↑ или ↓). Или, что то же самое, при обходе вокруг центра вихря общая фаза конденсата и относительная фаза двух компонент меняются на ±π.

Одномерным аналогом такого возбуждения является темный полусолитон со скачком фазы на ±π в одной из компонент. В этом эксперименте наблюдалось формирование полусолитонов при обтекании бозе-конденсатом экситонных поляритонов препятствия со сверхкритической скоростью. Как показано на диаграммах снизу для интенсивности и фазы излучения при двух поляризациях, а также степени циркулярной поляризации, по обе стороны от препятствия образуются две пары солитон-антисолитонов, простирающиеся вниз по течению в виде полос со скачками фазы.

Любопытно также, что полусолитоны под действием псевдомагнитного поля подвергаются ускорению со стороны такой же силы, которая действовала бы на магнитные монополи.

#поляритоны #бозе_конденсация

Вот это красивый эксперимент: лазерное охлаждение наномеханического осциллятора почти до основного состояния, ограниченное лишь квантовым пределом дробового шума.

Этот метод, называемый методом боковой полосы, похож на доплеровское охлаждение атомного газа. Как показано на рисунке, осциллятор (мембрана из Si₃N₄ толщиной 40 нм) облучается лазерным светом, который рассеивается с испусканием (стоксова компонента, красная линия) либо поглощением (антистоксова компонента, синяя) фонона осциллятора. Мембрана помещена в оптическую полость, спектральная линия которой (серая кривая) резонансно усиливает антистоксову компоненту, охлаждающую осциллятор, подавляя стоксову, которая его нагревает.

Как показано на графиках, антистоксовы процессы доминируют над стоксовыми до тех пор, пока не достигается предел, при котором фактор резонансного усиления первых не скомпенсируется разностью их собственных скоростей (n против n+1). Среднее число фотонов в механическом осцилляторе при этом снижается до n ≈ 0.2.

#фотоника

Красивый эксперимент с созданием управляемых потенциальных ям для экситонов в двумерном MoSe₂. Например, верхний затвор с круговым отверстием, в сочетании с нижним сплошным затвором, создают для экситонов кольцеобразную потенциальную яму, в которой образуются дискретные связанные состояния.

На диаграмме справа показан спектр отражения такой структуры при различных напряжениях на нижнем затворе (по горизонтали). Последнее устанавливает общий уровень допирования в областях внутри и снаружи кругового отверстия, в зависимости от которого устанавливаются разные режимы, обозначенные римскими цифрами.

Можно видеть, что набор дискретных экситонных уровней в кольцеобразной яме проявляется в режиме III, когда область снаружи допирована электронами, а внутри – дырками. В некоторых режимах можно видеть спектральную линию триона при меньшей энергии 1.61 эВ.

#экситоны #дихалькогениды_переходных_металлов

Можно ли при измерении проекции спина ½ получить значение 100? Так озаглавлена классическая статья Ааронова, Альберта и Вайдмана, в которой было введено понятие слабых значений – то есть значений наблюдаемых величин, получаемых при слабых измерениях.

Слабое значение наблюдаемой величины A в состоянии |ψ> – это величина <φ|A|ψ>/<φ|ψ>, которую можно измерить в эксперименте, вводя систему в «слабое» взаимодействие с измерительным прибором и затем проецируя получающийся вектор состояния на некоторое состояние |φ>. «Слабость» состоит в том, что изменение состояния системы в ходе взаимодействия системы с измерительным прибором должно быть незначительно: иными словами, оператор соответствующей унитарной эволюции должен мало отличаться от единичного.

Слабые значения ведут себя странно: они могут выходить за пределы спектра оператора измеряемой величины и, вообще говоря, комплексны. Неудивительно, что эта работа породила множество споров насчет того, каков физический смысл имеют слабые значения.

#квантовая_механика

А вот классический пример того, как можно измерить слабое значение.

Пучок частиц со спином ½ последовательно пропускается через два аппарата Штерна-Герлаха, в которых неоднородное магнитное поле растягивает в противоположные стороны частицы с разными направлениями спина. При этом первый аппарат, ориентированный вдоль оси z, действует на пучок частиц очень слабо, не разделяя его полностью, а лишь слегка смещая и растягивая. Второй же аппарат, ориентированный вдоль оси x, является сильным, деля пучок на две половины, одна из которых и направляется на фотопластинку.

Набирая достаточную статистику (это ключевая черта слабых измерений – их нужно повторять много раз для достаточной точности результата), можно измерить смещение пятна δz на фотопластинке, пропорциональное слабому значению величины σ_z, спроецированному вторым аппаратом на состояние ↑_x. Если угол α между начальным направлением спина ξ и осью x близок к π, слабое значение проекции спина может выходить за «физический» предел ½.

#квантовая_механика

Как я писал выше, слабые значения наблюдаемых величин в квантовой механики могут принимать «нефизические» значения: например, проекция спина ½ на ось z может иметь слабое значение 100. Является ли это проблемой или, наоборот, важной особенностью квантовой механики?

В этой работе было показано, что аномальность слабых значений является признаком квантовой контекстуальности – поведения квантовой системы, выходящего за рамки «наивного» представления о том, что все наблюдаемые еще до их измерения имеют определенные значения. Автор работы называет аномальными те слабые значения <φ|A|ψ>/<φ|ψ> наблюдаемой величины A, вещественная часть которых выходит за границы спектра оператора A (которые либо выше его максимального собственного значения, либо ниже минимального).

Упомянутое выше «наивное» представление называется, в противовес, неконтекстуальностью. Это, по существу, теория скрытых параметров – интуитивно понятное нам представление о том, что все частицы в квантовой механике «на самом деле» имеют определенные координаты еще до их измерения (равно как и спины частиц уже имеют определенные направления). Процесс измерения лишь выявляет эти координаты или ориентации спинов, до поры до времени «скрытые» от нас – заранее определенные, хотя и случайно варьирующиеся при каждом повторении эксперимента. Точно так же, бросая монету и зажимая ее в кулак, мы не знаем, выпал ли на ней орел или решка, пока не разожмем пальцы и не посмотрим на нее – хотя мы уверены, что это значение уже точно определено, только до поры до времени нам не известно.

Слово «неконтекстуальность» здесь означает, что «скрытые» значения наблюдаемых величин (уже определенные, но пока нам не известные) не зависят от контекста – например, значений других, коммутирующих с ними наблюдаемых. Контекстуальность же, возникающая при аномальных слабых значениях, говорит о том, что такой наивный реализм в квантовой механике не работает. Иными словами, «точные» координаты и направления спинов до самого момента измерения не являются точно определенными. Они определяются только в процессе измерения, причем совместно: координата одной частицы может завесить от того, какой при этом окажется координата другой, запутанной с ней частицы (то есть коммутирующая с ней величина – тот самый контекст).

Самые известные примеры контекстуальности – это нарушение неравенств Белла при измерении статистики направлений спинов запутанной пары частиц и парадокс Харди, при котором две частицы, вроде как, должны одновременно и находиться в одной точке пространстве, и не должны там встретиться.

#квантовая_механика #отвал_башки #объяснения

Киральный магнитный эффект – это появление тока j = αB, параллельного приложенному магнитному полю B, в топологических вейлевских полуметаллах. Для появления такого тока требуется наличие дисбаланса уровней Ферми в вейлевских точках противоположных киральностей.

Хотя статический киральный магнитный эффект (постоянный ток j вдоль постоянного магнитного поля B) противоречит теореме Блоха об отсутствии токов в T-симметричной системе в термодинамическом равновесии, считается, что может существовать динамический киральный магнитный эффект – возникновение осциллирующего j при медленных осцилляциях B.

В этой работе показана любопытная вещь: оказывается, киральный магнитный эффект – это другая сторона гиротропного магнитного эффекта, то есть появления у вещества магнитного момента во внешнем электрическом поле. Этот магнитный момент создается электронами, движущимися по поверхности Ферми.

Связь двух эффектов можно понять вот как: магнитное поле B создает ток j = αB благодаря киральному магнитному эффекту. Но это же магнитное поле, взятое в виде медленно осциллирующей и длинноволновой плоской волны создает поперечное электрическое поле E, которое, благодаря гиротропному магнитному эффекту, индуцирует намагниченность M = (–i/ω)αE. А эта намагниченность, в свою очередь, связана с током j, так что оба эффекта сводятся друг к другу.

Оба этих эффекта характеризуются одним и тем же коэффициентом α, который может быть вычислен как интеграл по поверхности Ферми от произведения скорости Ферми электронов на их орбитальный магнитный момент, обусловленный кривизной Берри.

#топологические_материалы #электродинамика

А ведь действительно: представим, что мы считаем отклик материала на электрическое поле с частотой ω и волновым вектором q. Если мы сначала берем предел q → 0, получая однородное поле, осциллирующее с частотой ω, мы можем посчитать проводимость σ(ω). Взяв после этого предел ω → 0, мы находим статическую проводимость.

Если же, наоборот, мы сначала берем предел ω → 0, у нас получается отклик материала на неподвижный пространственно неоднородный потенциал с волновым вектором q. Материал откликается на него перераспределением своей электронной плотности. В пределе q → 0 мы можем найти электронную сжимаемость материала – отклик электронной плотности на однородный по пространству сдвиг электрохимического потенциала.

#электродинамика #твердое_тело #цитаты

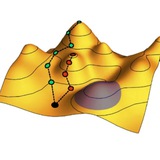
Занятная работа: в ней предсказана флоке-делокализация связанного состояния частицы, изначально находящегося в трехмерной потенциальной яме, под действием вращающегося электрического поля.

«На пальцах» ее можно объяснить так: вращающееся поле протаскивает частицу по кругу, так что в системе ее покоя изначально сферическая потенциальная яма (зеленый шар) начинает вращаться, размазываясь в среднем в яму тороидальной формы. Чем больше радиус тора r₀ по сравнению с изначальным радиусом ямы a, тем слабее связано состояние частицы в тороидальной ямы.

Как показано на графиках, при некотором критическом радиусе r₀ связанное состояние пропадает. Можно сказать, что частица делокализуется, выскакивая из потенциальной ямы под действием внешнего облучения, из-за изменения топологии эффективного удерживающего потенциала: односвязная потенциальная яма превращается в двухсвязную.

#квантовая_механика #состояния_Флоке

Если на когерентное фотонное состояние |α> подействовать оператором уничтожения a, мы получим снова когерентное состояние: a|α> = α|α>. При действии же оператора рождения a⁺ получится то, что называется когерентным состоянием с добавленным фотоном: a⁺|α> = |α,1>.

В этом эксперименте подобные состояния были приготовлены и исследованы при помощи квантовой томографии. Для этого в нелинейно-оптический кристалл запускали |α> и дожидались, когда в нем произойдет спонтанное параметрическое рассеяние с испусканием двух фотонов, один из которых добавляется к |α>, а второй идет в детектор.

На диаграммах справа показаны измеренные функции Вигнера состояния |α,1> при разных значениях |α|. В пределе α → 0 мы получаем фоковское состояние с одним фотоном: оно существенно квантовое, о чем говорят отрицательная функция Вигнера в центре. При |α| >> 1 восстанавливается квазиклассическое когерентное состояние. Таким образом, изменение α позволяет плавно переходить от «квантового» состояния фотонов к «классическому».

#фотоника

Эта высокоцитируемая статья 2012 года – одна из ключевых теоретических работ, обративших внимание исследователей на необычные свойства двумерных дихалькогенидов переходных металлов.

Авторы при помощи относительно простой модели показывают, что:
• Зонная структура описывается моделью массивных дираковских электронов в двух долинах K и K´.
• В валентной зоне имеется сильное спин-орбитальное расщепление, причем его знаки противоположны в двух долинах.
• Межзонные оптические переходы разрешены для правой циркулярной поляризации в долине K и для левой в долине K´.
• Кривизна Берри противоположна в двух долинах, что может приводить к долинному эффекту Холла.
• При допировании дырками лишь одной из спин-орбитально расщепленных подзон валентной зоны долинный эффект Холла становится заодно еще и спиновым.
• Накачивая материал двумя лазерными лучами с противоположными циркулярными поляризациями и с разными частотами, можно добиться и обычного – зарядового – эффекта Холла.

#дихалькогениды_переходных_металлов

Весьма известная в узких кругах теоретиков классическая работа, в которой было показано, как друдевский и сверхтекучий веса связаны с корреляционной функцией токов Λ(q, ω).

Как показано на рисунке, друдевский вес D связан с пределом функции Λ(q, ω), в котором мы сначала устремляем к нулю q, и только затем ω. Это парамагнитный вклад в D. Второй, диамагнитный вклад дается средним значением локальной кинетической энергии <–k_x>.

Сверхтекучий вес D_s дается обратным порядком пределов функции Λ(q, ω): сначала ω → 0, затем q → 0, при этом нужно брать поперечную часть тензора Λ. Все это потому, что D_s, с физической точки зрения, связан с эффектом Мейснера, а значит – с откликом на статический длинноволновый поперечный векторный потенциал магнитного поля.

В зависимости от значений D и D_s, получается следующая классификация материалов:
• D > 0, D_s = 0 – металл.
• D > 0, D_s > 0 – сверхпроводник.
• D = 0, D_s = 0 – изолятор.

#твердое_тело #сверхпроводимость #сверхтекучесть

А вот очень известная и также классическая статья, в которой было введено понятие максимально локализованных функций Ванье, а также был разработан алгоритм для их вычисления. Такие функции широко используются как базисные во многих расчетных методах, таких как DFT.

В модели сильной связи блоховская функция |u_nk> приближенно представляется как линейная комбинация волновых функций орбиталей, распределенных по ячейкам кристалла. Соответственно, функции Ванье |Rn> получаются обратным преобразованием Фурье по квазиимпульсу блоховских функций |u_nk>: это дает возможность собрать обратно некий аналог «орбитали», находящейся в ячейке R для энергетической зоны n, но уже не приближенной, а точной.

Проблема в том, что функции |u_nk> определены с точностью до произвольной фазы, своей для каждого k. Из-за таких калибровочных преобразований функции Ванье могут деформироваться. Авторы предложили определять калибровку так, чтобы суммарная дисперсия функций Ванье в пространстве Ω была минимальной.

#твердое_тело

Интересное обстоятельство из статьи из предыдущего поста: функционал Марцари-Вандербильта Ω, минимизация которого дает максимально локализованные функции Ванье, может быть разбит на две части.

Первая часть не зависит от калибровки блоховских функций (относительно которых производится минимизация всего Ω) и поэтому не может быть минимизирована. Вторая же часть от калибровки зависит: она может быть минимизирована до нуля в одномерном случае, но не в двумерном и трехмерном из-за некоммутации операторов координат PxP, PyP, PzP, спроецированных на рассматриваемую энергетическую зону оператором проекции P.

Первая, калибровочно инвариантная, часть функционала весьма любопытна: она может интерпретироваться как степень делокализации по координатам самого проекционного оператора P. Впоследствии выяснилось, что она ограничена топологическим инвариантом зоны – ее числом Черна. Таким образом, топологическая нетривиальность электронных состояний в кристалле подразумевает их делокализацию в пространстве.

#твердое_тело

А вот пара картинок из статьи Марцари и Вандербильта с примерами максимально локализованных функций Ванье.

Слева представлена одна из таких функций в валентной зоне кристалла кремния, показанная в пространстве и в разрезе вдоль химической связи между соседними атомами. Справа – примеры двух функций в молекуле этилена C₂H₄, сосредоточенных вблизи σ-связи между водородом и углеродом и вблизи двойной σπ-связи между двумя атомами углерода.

Как видно, максимально локализованные функции Ванье, помимо своих технических преимуществ для расчетов, очень близки к тому, что мы понимаем под «молекулярными орбиталями» – несмотря на то, что в протяженной и многочастичной системе никаких настоящих молекулярных орбиталей не существует, поскольку электроны распределены по кристаллу и квантовой запутаны между собой.

#твердое_тело #химия

Интересная работа, в которой был разработан метод машинного обучения, который позволяет – в теории – улучшить процесс интеграции беженцев.

Модель обучается, анализируя накопленные данные о том, кто из беженцев, направленный в какое место расселения, смог найти там работу в течение 90 дней. При этом каждый беженец имеет набор характеристик: возраст, национальность, знание языков, уровень образования и т.д. Модель, по идее, улавливает закономерности (в том числе неочевидные) между этими характеристиками и шансами нахождения работы в каждом месте расселения, после чего выдает рекомендации, куда направить какую семью беженцев, чтобы эти шансы увеличить.

На диаграммах показано сравнение шансов нахождения работы в течение 90 дней, разбитых по районам расселения в США и Швейцарии, получающихся при имеющейся практике распределения (красные) и прогнозируемых при использовании рекомендаций машинного алгоритма (голубые). Во втором случае шансы должны увеличиться в среднем в полтора-два раза.

#популярное #общество