Занятная работа: в ней на примере системы электронов, взаимодействующих с фононами, примесями и между собой, критически анализируются «общепринятые факты», касающиеся релаксации неравновесных многоэлектронных систем после накачки.

В частности, авторы рассматривают два расхожих утверждения:
(1) Скорость релаксации возбужденных квазичастиц дается их собственно-энергетической частью: τ⁻¹(ω) = –2 Im Σ(ω).
(2) При наличии нескольких каналов релаксации их скорости складываются: τ⁻¹ = (τ₁)⁻¹ + (τ₂)⁻¹ + …, это называют правилом Матиссена. Действительно, если возбужденное состояние может распадаться, к примеру, сразу по нескольким каналам, то динамика его населенности меняется согласно уравнению dn/dt = –n/ τ₁– n/ τ₂– … В итоге мы получаем экспоненциальную релаксацию n(t) ~ exp(–t/τ) с суммарной скоростью τ⁻¹.

В статье показывается, что на практике оба этих утверждения часто нарушаются. С первым тезисом проблема в том, что собственно-энергетическая часть Σ(ω), по-хорошему, описывает релаксацию одноэлектронной функции Грина G(t, t´) неравновесной системы как функцию относительного времени – разности ее аргументов t – t´. А такие наблюдаемые величины, как населенность возбужденных состояний, коэффициент отражения материала после накачки и другие, измеряются как функции времени задержки после накачки, то есть среднего времени (t + t´)/2. Таким образом, переносить релаксацию вдоль одной переменной на динамику вдоль другой переменной можно лишь с натяжкой.

Что касается второго тезиса, он противоречит часто наблюдаемым процессам мультиэкспоненциального распада: когда сначала наблюдаемая величина релаксирует быстро, с одним временем τ₁, потом спадает медленнее, с временем τ₂, потом может выявиться еще большее, третье время распада и т.д. Такое поведение – с разделением времен распада вместо их суммирования – не согласуется с правилом Матиссена и показывает, что уравнение для динамики распада должно иметь более сложный вид, чем показано выше.

Мультиэкспоненциальный распад требует наличия бутылочных горлышек, при которых разные каналы распада не идут одновременно с самого начала, а, к примеру, завершение одного канала распада является условием для начала второго. К примеру, термализация электронного газа после накачки, происходящая за счет электрон-электронных столкновений (первый, быстрый канал распада) должна завершиться для того, чтобы потом началось эффективное охлаждение электронов посредством испускания фононов (второй, более медленный канал).

#твердое_тело #открытые_квантовые_системы #фотоника

А вот поучительная иллюстрация из той же статьи, демонстрирующая релаксацию электронов после накачки под действием различных факторов. Это результат расчета распределения электронов по импульсам и энергии до прибытия импульса накачки (левый столбец диаграмм), во время накачки (центральный столбец) и спустя 86 фс после него (правый столбец).

При включении одного лишь электрон-фононного взаимодействия (первая строка диаграмм). Электроны могут отдать свою энергию фононам в области энергий шириной в две фононные частоты вокруг уровня Ферми. Как видно, в этой полосе эффективно идут процессы охлаждения.

Одно лишь рассеяние электронов на примесях (вторая строка) делает распределение изотропным, но не приводит к термализации по оси энергии в силу своей упругости.

В свою очередь, одно лишь электрон-электронное взаимодействие (третья строка) приводит к установлению теплового распределения Ферми-Дирака, но горячего, поскольку электронам некуда отдавать свою энергию.

#твердое_тело #открытые_квантовые_системы

Интересная работа о том, использует ли природа квантовые эффекты для увеличения эффективности фотосинтеза. А именно: является ли перенос энергии экситонами от места поглощения фотона к реакционному центру чисто квантовой последовательностью перескоков, чисто классической диффузией или же чем-то промежуточным?

Моделирование показывает, что при реалистичных условиях перенос происходит в промежуточном, частично когерентном режиме. Любопытно, что в этом режиме возбуждение распределено равномерно по всей цепочке переноса (ENAQT regime на рисунке) – вместо осцилляций в квантовом режиме или экспоненциального спадания в классическом режиме. Это делает эффективность переноса не только более высокой, но и весьма устойчивой к изменениям структуры молекулярного комплекса.

Хотя выигрыш в эффективности переноса здесь не так уж велик, чтобы служить движущей силой отбора. По-видимому, это либо случайное совпадение, либо результат приспособления к каким-то другим факторам отбора.

#биология #открытые_квантовые_системы

Вот это чумовой эксперимент, в котором удалось наблюдать отклик WSe₂ на терагерцовые импульсы с разрешением до 0.3 фс, которое авторы назвали аттосекундным.

Идея метода показана на рисунке. Поле терагерцового импульса (c) разрывает экситон, имеющийся в многослойном WSe₂, на электрон и дырку – синий и красный шарики на панели (a). В системе покоя дырки электрон разгоняется полем сначала в одну сторону, потом обратно, пока не произойдет его обратное столкновение с дыркой. Излучение, испускаемое при этом столкновении, дает вклад в боковую полосу частот.

На панели (b) то же самое происходит в монослое WSe₂, где кулоновское притяжение электрона и дырки сильнее, из-за чего обратное столкновение происходит раньше. Сравнивая излучения в боковой полосе как функции времени в толстом материале и в монослое (d-e), можно видеть разность времен обратного столкновения – результат влияния многочастичных эффектов на динамику электронов и дырок – с разрешением меньше 1 фс.

#фотоника #дихалькогениды_переходных_металлов

Смотришь такой на модель, которую авторы теоретической работы обещают рассмотреть: куча электронов, между которыми имеется кулоновское отталкивание, а еще все эти электроны взаимодействуют с кучей мод квантованного электромагнитного поля (а значит, еще и дополнительно воздействуют друг на друга через запаздывающее поперечное поле), а еще включается член A² и противовращающие члены...

И думаешь: «ничего себе, какая амбициозная задача здесь ставится!» 😱

А потом авторы пишут: ну, для простоты кулоновское взаимодействие мы сейчас выключим, а для фотонов возьмем только одну моду с частотой ω, да и саму эту моду возьмем пространственно однородной...

И думаешь: «ну да, как всегда...» 😏

#электродинамика #цитаты

В этой работе рассмотрено, что происходит с двумерным электронным газом в резонаторе Фабри-Перо в режиме сильной связи – с «честным» учетом взаимодействия электронов с модами полости, включая член A².

Авторы показывают, что взаимодействие электронов с модами полости приводит к перенормировке их свойств: эффективная масса электронов повышается а в спектре проводимости появляются поляритонные резонансы, забирающие часть спектрального веса. Как результат, друдевский вес электронного газа уменьшается и при критической величине силы связи становится нулевым. При сверхкритической силе связи сфера Ферми электронного газа становится неустойчивой: вместо нее возникает что-то вроде уровней Ландау, но основного состояния у системы уже не существует.

Еще один интересный эффект – это превращение обычной, притягивающей силы Казимира между зеркалами полости в отталкивающую из-за наличия внутри электронного газа.

#электродинамика #фотоника

Обымчный электрон vs. электрон, одетый в шубу благодаря взаимодействию с электромагнитным вакуумом.

#цитаты #фотоника

Свежий обзор по квантовым батареям – устройствам хранения энергии, использующим эффекты квантовой когерентности и квантовой запутанности для получения превосходства над классическими системами в скорости зарядки и разрядки.

К примеру, классическая батарея, состоящая из N одинаковых частей, может заряжаться и разряжаться со скоростью, растущей пропорционально N (или еще медленнее), а квантовая батарея может делать это со скоростью ~N². Механизм, позволяющей квантовой батарее получать преимущество в скорости передачи энергии, схож со сверхизлучением Дике – когерентным взаимодействием множества кубитов с одной и той же электромагнитной модой, усиливающимся за счет конструктивной интерференции.

В обзоре подробно рассматриваются все теоретические аспекты устройства и работы квантовых батарей: хранение энергии и ее утечка, зарядка и разрядка, фундаментальные ограничения на их скорость, возможные реализации и т.д. А успешных экспериментов в этой области – пока что всего пара штук.

#квантовая_термодинамика

Красивое: структура из сплава железа с никелем, напечатанная на 3D-принтере. Она обладает алмазоподобной решеткой и имитирует спиновый лед – материал, в котором за счет магнитной фрустрации образуются эффективные магнитные монополи.

#твердое_тело

Это одна из работ сотрудников Гугла, в которой разрабатывались модели нейросетей, использующие механизм внимания и превратившиеся, в конце концов, в знаменитый ChatGPT. Как я подробнее писал раньше, механизм внимания анализирует каждое слово входного предложения и присваивает ему определенный вес в меру того, насколько важно оно в контексте текущей задачи.

Здесь этот механизм используется для решения задачи сопоставления предложений: нейронная сеть должна проанализировать два предложения и определить, является ли второе предложение следствием первого, противоречит ему или нейтрально по отношению к нему по смыслу. Например, «Боб не может заснуть из-за грозы на улице» и «Боб бодрствует» (следствие) либо «На улице солнечно» (противоречие).

Авторы показывают, что их модель достигает таких же результатов, как и традиционные нейросети без механизма внимания, используя на порядок меньшее число параметров. На рисунке показан пример матрицы весов внимания, связывающих слова обоих предложений.

#нейронные_сети

Красивый эксперимент с наблюдением тонкой структуры уровней Ландау в графене, обнаруживаемой в картине квантовой емкости. Как известно, квантовая емкость, дающая вклад в общую емкость между графеном и подложкой, примерно пропорциональна термодинамической плотности состояний dn/dμ: она велика при попадании уровня Ферми в уширенный энергетический уровень и зануляется в щелях.

На панелях C, D, E показана зависимость емкости графена от уровня допирования – это разрезы картины с панели B, взятые при фиксированных магнитных полях. В поле 2 Тл видно расщепление 0-го уровня Ландау на 4 подуровня (панель C) и гораздо менее выраженные расщепления остальных уровней. В более сильном поле 13.5 Тл видны дополнительные щели уже внутри каждого расщепленного подуровня 0-го уровня Ландау (панель D). При увеличении (панель E) видно, что это щели, связанные с возникновением дробного эффекта Холла.

#графен #уровни_Ландау

Оптическая полость обычно получается складыванием двух многослойных брэгговских зеркал, представленных стопками слоев диэлектрика толщиной в четверть длины волны. Большая суммарная толщина таких зеркал – проблема для миниатюризации устройств фотоники.

В этой работе авторы попытались сделать полость, использовав в качестве зеркал два слоя двумерного дихалькогенида переходного металла MoSe₂. Конечно, каждый монослой почти ничего не отражает, но вблизи экситонного резонанса их коэффициенты отражения резко увеличиваются, как показано на графиках справа.

На диаграмме снизу можно видеть спектральную линию моды полости, возникающую благодаря такому усиленному отражению от двух монослоев. Согласно расчетам, у нее не супер-высокая добротность – порядка 1000, зато полость получается весьма компактной. Любопытно также, что наложение внешнего магнитного поля позволяет расщеплять моду полости по направлениям циркулярной поляризации.

#дихалькогениды_переходных_металлов #поляритоны

Свежий эксперимент с бозе-конденсацией экситонных поляритонов в оптической микрополости, в котором был открыт новый скейлинговый закон – никто из теоретиков его не предсказывал.

Здесь измерялась когерентная фракция – величина, имеющая смысл доли частиц, принимающих участие в интерференционных эффектах. Она определяется по контрастности интерференционной картины, полученной наложением люминесцентного излучения от конденсата на его зеркально отраженную копию. Примеры таких картин при разных интенсивностях накачки показаны слева.

Когерентная фракция – это альтернатива доле конденсата для случая двумерных систем, где последняя плохо определена из-за формального отсутствия бозе-конденсации. Как показано на графике, когерентная фракция растет как полная плотность поляритонов в степени 3.2, пока не подходит к максимальному значению 1. Это и есть новый открытый закон. Степенная зависимость простирается на несколько порядков, причем как ниже, так и выше порога конденсации (пунктира).

#поляритоны #бозе_конденсация

А вот еще красивая картинка из статьи из предыдущего поста. Разрешенный по импульсу спектр люминесцентного излучения от поляритонов интегрируется по импульсу с получением зависимости интенсивности излучения от одной лишь энергии. Эта зависимость дает информацию о статистике чисел заполнения N(E) экситонных поляритонов.

Как показано справа, при каждой интенсивности накачки она фитируется распределением Бозе-Эйнштейна с какими-то температурой и химическим потенциалом (это тонкие черные кривые). Кстати говоря, здесь можно видеть, когда становится важна квантовая статистика бозонов, то есть когда их состояние становится вырожденным: это происходит, если N(E) превышает единицу.

Нижний график показывает результат фитирования: химический потенциал как функцию плотности поляритонов. Мы видим почти классическую «картинку из учебника», где химический потенциал на пороге конденсации подходит к нулю. Правда, из-за двумерности и конечности системы эта картина получается сильно смазанной.

#поляритоны #бозе_конденсация

Одна из важных моделей теории игр – это игра миноритариев (minority game), которая имитирует, на самом базовом уровне, поведение рынка.

В этой коллективной игре на каждом шаге игроки выбирают одно из двух действий – продавать актив или покупать его. Выигрыш получают те игроки, которые оказываются в меньшинстве: к примеру, продают актив в то время, когда большинство его покупает, из-за чего он сильно дорожает. Игроки могут принимать решение о продаже или покупке в зависимости от некоторой публичной информации и от собственной истории успехов или неудач.

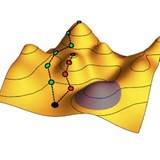
Оказывается, динамика поведения игроков в такой игре оказывается похожа на динамику спинового стекла, а число локальных равновесий Нэша может достигать огромных величин – как и число локальных минимумов энергетического ландшафта спинового стекла. В этой работе было показано, что в игре миноритариев может происходить нарушение симметрии реплик – дробление ландшафта коллективных стратегий игроков на несвязанные друг с другом бассейны.

#стекла #общество

Известная работа 2008 года, в которой было показано, что в фотонных кристаллах могут существовать связанные состояния в континууме для электромагнитного поля.

Пример показан на рисунке. В дифракционной решетке, представленной слоем диэлектрика с периодическими разрывами, может существовать волноводная мода, которая из-за разрывов становится утекающей. Как показано на панели (b), в спектре одной решетки, взятом при фиксированном волновом векторе вдоль нее k_x, такая мода проявляется в виде резонанса с конечным временем жизни.

Если же взять две параллельные решетки, то мода расщепляется на симметричную и антисимметричную. Первая из них и становится связанным состоянием в континууме, демонстрируя концентрацию поля между решетками. Как показано на панели (c), антисимметричная мода остается утекающей, а спектральная линия симметричной моды становится предельно узкой. В отсутствие диссипации ее добротность становится формально бесконечной: мода отвязывается от континуума и становится связанной.

#электродинамика

Вот это занятная работа, в которой предлагается концепция термодинамического компьютера, решающего задачи линейной алгебры: линейные уравнения, решение уравнения Ляпунова, обращение матрицы и расчет ее определителя. Авторы показывают, что при больших размерностях он имеет степенное преимущество над обычными численными методами.

Сверху показана схема решения системы линейных уравнений Ax = b. Нужно создать систему гармонических осцилляторов с гамильтонианом H = ½xᵀAx – bᵀx, где матрица A задает упругости пружин, а b отвечает действующим на частицы внешним силам. Тогда измеряемые в эксперименте средние координаты осцилляторов дадут искомое решение x = A⁻¹b.

Как показано на графиках, термодинамический метод проигрывает по точности, например, методу сопряженных градиентов при небольших размерах задачи (d = 100), но при больших размерах (d = 5000) уже сильно выигрывает. Он может быть полезен, когда нужно быстро получить приближенное решение задачи большого размера.

#термодинамика #отвал_башки

А вот красивая иллюстрация из статьи из предыдущего поста, демонстрирующая стремление гармонического осциллятора к термодинамическому равновесию.

Слева – численное решение уравнения Ланжевена, показывающее траекторию частицы в квадратичном потенциале эллиптической формы. Как видно, частица сначала диффундирует к центру удерживающего потенциала, а затем блуждает, повторяя его форму гауссовой статистикой своих координат.

Справа показано, как с течением времени эволюционирует уже не координата одной частицы, а ее статистическое распределение, показанное линиями равной высоты. Оно получено решением уравнения Фоккера-Планка и характеризует уже весь ансамбль траекторий частиц.

Если набрать достаточную статистику, то вектор средних координат частицы <x> даcт «термодинамическое» решение системы линейных уравнений x = A⁻¹b, а их ковариации <ΔxᵤΔxᵥ> (то есть разброс относительно средних) дадут элементы обратной матрицы A⁻¹.

#стохастическая_термодинамика

Среди двумерных дихалькогенидов переходных металлов есть материалы с весьма интересными свойствами: анизотропные, топологически нетривальные, экситонные диэлектрики и т.д. В этой работе показано, что допированный молибденом двумерный кристалл WTe₂ обладает анизотропным оптическим откликом и гиперболичностью в некоторой полосе частот.

На графиках показаны результаты измерений коэффициента поглощения (левый столбец графиков) и извлеченные из них частотные зависимости Im σ (правый столбец) для двух направлений линейной поляризации. Три строки диаграмм отвечают разным уровням допирования молибденом x. Серым цветом показаны области гиперболичности, где Im σ в двух направлениях имеют разные знаки – она находится в дальнем инфракрасном диапазоне.

В эксперименте авторы каким-то запутанным образом подтверждают существование гиперболических плазмонов, изготавливая из материала массивы нанолент, вырезанных под разными углами, и измеряя их спектры поглощения.

#дихалькогениды_переходных_металлов

Недавно я писал о квантовых батареях – устройствах хранения энергии, использующих квантовые эффекты для увеличения скорости ее накопления или отдачи. А вот работа, в которой исследовались фундаментальные пределы для скорости таких процессов.

Авторы показывают, что скорость P обмена энергией между квантовой батареей и окружением (то есть скорость зарядки или разрядки) ограничена неравенством P ≤ ΔH×√I_E, где ΔH – разброс энергий батареи, I_E – фишеровская информация, определяющая, насколько быстро статистическое распределение энергий батареи меняется с течением времени.

При этом I_E ≤ I_Q, где I_Q – квантовая фишеровская информация, показывающая, насколько быстро с течением времени изменяется матрица плотности батареи. Действительно, как показано на рисунке, в пространстве квантовых состояний (сверху) система может двигаться быстрее, чем в пространстве распределений энергии (снизу). С точки зрения эффективности батареи, это излишний расход ресурсов, потому что важна только I_E.

#квантовая_термодинамика

А вот пример того, как работает квантовое преимущество при зарядке квантовой батареи. Здесь рассматривается простейшая модель батареи в виде набора невзаимодействующих кубитов с гамильтонианом H_B. Квантовость системы вступает в игру в процессе ее зарядки, через гамильтониан взаимодействия H_C батареи с окружающей средой.

Первый вариант такого гамильтониана, показанный на рисунке слева, отвечает параллельной зарядке: каждый кубит перекачивается из основного состояния в возбужденное через действующий на него оператор σ_x. Второй вариант (справа) отвечает глобальной зарядке: это тензорное произведение всех операторов σ_x, а не их сумма.

Диаграммы показывают, как с течением времени меняется распределение энергий батареи. В случае параллельной зарядки батарея последовательно взбирается вверх по энергии, от каждого многочастичного уровня энергии к соседнему. При глобальной же зарядке система сразу переходит из основного состояния в наивысшее возбужденное, минуя промежуточные стадии.

#квантовая_термодинамика