«Это приближение часто используется, хотя оно и неправильно» – это из статьи из предыдущего поста.
#цитаты
#цитаты
😁5😱1
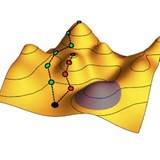
Классическая работа с выводом того, что сейчас называют формулой Онзагера-Мэчлапа. Эта формула дает вероятность того, что статистическая система, в ходе своей неравновесной динамики, пройдет по определенной траектории в пространстве параметров. К примеру, мы с течением времени увеличиваем давление на поршень в сосуде с газом и хотим понять, с какой вероятностью координата прошня пройдет по траектории x(t).
Среди всех траекторий, по которым может пойти система, есть наиболее вероятная – она дается обычной неравновесной термодинамикой. А есть флуктуации, вероятность которых гауссовым образом спадает при удалении от нее. Таким образом, вероятность траектории дается интегралом по путям. С современной точки зрения, формула Онзагера-Мэчлапа – это лишь гауссово приближение для флуктуаций, справедливо для достаточно больших систем и не очень сильных отклонений от равновесия.
А еще в этой работе был получен известный в неравновесной термодинамике принцип минимальной диссипации.
#стохастическая_термодинамика
Среди всех траекторий, по которым может пойти система, есть наиболее вероятная – она дается обычной неравновесной термодинамикой. А есть флуктуации, вероятность которых гауссовым образом спадает при удалении от нее. Таким образом, вероятность траектории дается интегралом по путям. С современной точки зрения, формула Онзагера-Мэчлапа – это лишь гауссово приближение для флуктуаций, справедливо для достаточно больших систем и не очень сильных отклонений от равновесия.
А еще в этой работе был получен известный в неравновесной термодинамике принцип минимальной диссипации.
#стохастическая_термодинамика
Исключительные точки – это точки в пространстве параметров неэрмитового гамильтониана, в которых происходит бифуркация его собственных значений. В этой работе было предсказано существование весьма странных исключительных связанных состояний вблизи таких точек.
Главная патология таких состояний в том, что числа их заполнения могут быть меньше 0 или больше 1. Как следствие, в таких системах может возникать отрицательная энтропия запутанности – нонсенс с точки зрения квантовой информатики. Наша интуиция, согласно которой число заполнения должно быть 0 или 1 (или в промежутке между 0 или 1 в случае статистического ансамбля), для неэрмитовых систем не работает из-за несохранения в них плотности вероятности.
Волновые функции таких состояний (жирные кривые на графике снизу) тоже ведут себя аномально по сравнению с другими собственными функциями гамильтониана (тонкими кривыми). Автор усматривает некую аналогию такого поведения с излучением Хокинга вблизи горизонта черной дыры.
#неэрмитовы_системы #отвал_башки
Главная патология таких состояний в том, что числа их заполнения могут быть меньше 0 или больше 1. Как следствие, в таких системах может возникать отрицательная энтропия запутанности – нонсенс с точки зрения квантовой информатики. Наша интуиция, согласно которой число заполнения должно быть 0 или 1 (или в промежутке между 0 или 1 в случае статистического ансамбля), для неэрмитовых систем не работает из-за несохранения в них плотности вероятности.
Волновые функции таких состояний (жирные кривые на графике снизу) тоже ведут себя аномально по сравнению с другими собственными функциями гамильтониана (тонкими кривыми). Автор усматривает некую аналогию такого поведения с излучением Хокинга вблизи горизонта черной дыры.
#неэрмитовы_системы #отвал_башки
👍2
А вот объяснение того, почему для исключительных связанных состояний числа их заполнения выходят за границы физически осмысленного интервала от 0 до 1.
Введем одночастичную матрицу плотности P(x,x´) = <c⁺(x)c(x´)>. Ее собственные значения дают числа заполнения одночастичных состояний, потому что после перевода в диагональный вид она будет выглядеть как <aᵤ⁺aᵥ> = fᵤδᵤᵥ, где aᵤ – операторы этих одночастичных состояний, fᵤ = 0, 1 – числа их заполнения.
Так и происходит в случае обычных квантовых состояний, заполненных ниже уровня Ферми (пример слева на рисунке). В случае же исключительных связанных состояний (справа на рисунке) матрица P(x,x´) сильно делокализована и имеет много больших матричных элементов вдали от диагонали. Причина этому – патологическое поведение их волновых функций и дефективность гамильтониана (его собственные векторы не образуют полного базиса) в исключительной точке. Собственные значения такой матрицы легко могут выходить за границы интервала от 0 до 1.
#неэрмитовы_системы #отвал_башки
Введем одночастичную матрицу плотности P(x,x´) = <c⁺(x)c(x´)>. Ее собственные значения дают числа заполнения одночастичных состояний, потому что после перевода в диагональный вид она будет выглядеть как <aᵤ⁺aᵥ> = fᵤδᵤᵥ, где aᵤ – операторы этих одночастичных состояний, fᵤ = 0, 1 – числа их заполнения.
Так и происходит в случае обычных квантовых состояний, заполненных ниже уровня Ферми (пример слева на рисунке). В случае же исключительных связанных состояний (справа на рисунке) матрица P(x,x´) сильно делокализована и имеет много больших матричных элементов вдали от диагонали. Причина этому – патологическое поведение их волновых функций и дефективность гамильтониана (его собственные векторы не образуют полного базиса) в исключительной точке. Собственные значения такой матрицы легко могут выходить за границы интервала от 0 до 1.
#неэрмитовы_системы #отвал_башки
Кстати говоря, в работе из предыдущего поста авторы утверждают, что впервые экспериментально наблюдали исключительные связанные состояния, реализовав их на базе электрических цепей.
Хотя это не совсем так: у них лапласиан электрической цепи (матрица, связывающая токи на узлах с напряжениями на различных участках) воспроизводит не гамильтониан той неэрмитовой системы, которую они моделируют, а лишь одночастичную матрицу плотности P(x,x´) этой системы, предварительно посчитанную вручную. На частотах, отвечающих собственным значениям такой матрицы, электрическая цепь дает резонансный отклик.
Как показано на графике, в эксперименте наблюдаются 4 резонанса, аналогичные набору чисел заполнения – вероятностей того, что заполнено «квантовое состояние» неэрмитовой системы. Два центральных резонанса отвечают нормальным числам заполнения 0 и 1, а два боковых – патологическим числам заполнения –1 и 2, характерным для исключительных связанных состояний.
#неэрмитовы_системы #отвал_башки
Хотя это не совсем так: у них лапласиан электрической цепи (матрица, связывающая токи на узлах с напряжениями на различных участках) воспроизводит не гамильтониан той неэрмитовой системы, которую они моделируют, а лишь одночастичную матрицу плотности P(x,x´) этой системы, предварительно посчитанную вручную. На частотах, отвечающих собственным значениям такой матрицы, электрическая цепь дает резонансный отклик.
Как показано на графике, в эксперименте наблюдаются 4 резонанса, аналогичные набору чисел заполнения – вероятностей того, что заполнено «квантовое состояние» неэрмитовой системы. Два центральных резонанса отвечают нормальным числам заполнения 0 и 1, а два боковых – патологическим числам заполнения –1 и 2, характерным для исключительных связанных состояний.
#неэрмитовы_системы #отвал_башки
👍2
Накачка Таулеса – перемещение целого числа частиц из одного места в другое при обходе гамильтониана вокруг особой точки в пространстве параметров – неоднократно наблюдалась на различных физических платформах. А в этом эксперименте реализована существенно многочастичная накачка Таулеса, требующая наличия межчастичного взаимодействия.
Здесь рассмотрена модель Райса-Меле для атомов (a): одномерная цепочка с чередующимися интегралами перескока, меньший из которых равен δ, и асимметрией Δ энергий соседних узлов. В отсутствие отталкивания на узле (U = 0) обход на плоскости (δ, Δ) вокруг начала координат – особой точки – сдвигает 2 частицы на одну элементарную ячейку (b). При U > 0 эта особая точка расщепляется на две, и обход вокруг каждой из них перемещает уже по 1 частице (c)-(e).
Как видно на графике для измеряемой скорости сдвига как функции U, накачка работает только при попадании особой точки вдоль контура обхода, при промежуточных значениях U.
#атомные_газы #топологические_материалы
Здесь рассмотрена модель Райса-Меле для атомов (a): одномерная цепочка с чередующимися интегралами перескока, меньший из которых равен δ, и асимметрией Δ энергий соседних узлов. В отсутствие отталкивания на узле (U = 0) обход на плоскости (δ, Δ) вокруг начала координат – особой точки – сдвигает 2 частицы на одну элементарную ячейку (b). При U > 0 эта особая точка расщепляется на две, и обход вокруг каждой из них перемещает уже по 1 частице (c)-(e).
Как видно на графике для измеряемой скорости сдвига как функции U, накачка работает только при попадании особой точки вдоль контура обхода, при промежуточных значениях U.
#атомные_газы #топологические_материалы
👍2
А вот как обход в пространстве параметров вокруг особой точки (накачка Таулеса из статьи из предыдущего поста) должен выглядеть в идеале и как его пришлось осуществлять в реальности.
#цитаты #топологические_материалы
#цитаты #топологические_материалы
Авторы этой работы утверждают, что наблюдали кристалл квадрупольных экситонов в трехслойной структуре WSe₂/MoSe₂/WSe₂. Фазовая диаграмма такой системы показана на рисунке на осях плотности экситонов n_ex и отношения неких характерных энергий R. При достаточно больших R, по мере увеличения n_ex, фаза кристалла квадрупольных экситонов сменяется фазой дипольных межслойных экситонов, располагающихся в шахматном порядке.
Квадрупольность экситонов здесь в том, что они составлены одним электроном в центре и дыркой, распределенной в виде двух «половинок» в верхнем и нижнем слоях. Такой комплекс не имеет электрического дипольного момента, поэтому его радиационная рекомбинация сильно подавляется.
Верхний график показывает, как, при повышении температуры выше 25 К, экситонный кристалл расплавляется, а нижний – как, при плотности экситонов выше 5×10¹¹ см⁻², он распадается на дипольные межслойные экситоны, что приводит к резкому увеличению коэффициента диффузии.
#экситоны #дихалькогениды_переходных_металлов
Квадрупольность экситонов здесь в том, что они составлены одним электроном в центре и дыркой, распределенной в виде двух «половинок» в верхнем и нижнем слоях. Такой комплекс не имеет электрического дипольного момента, поэтому его радиационная рекомбинация сильно подавляется.
Верхний график показывает, как, при повышении температуры выше 25 К, экситонный кристалл расплавляется, а нижний – как, при плотности экситонов выше 5×10¹¹ см⁻², он распадается на дипольные межслойные экситоны, что приводит к резкому увеличению коэффициента диффузии.
#экситоны #дихалькогениды_переходных_металлов
А вот еще красивые диаграммы из работы, где наблюдали кристалл квадрупольных экситонов. Это спектры люминесценции как функции вертикального электрического поля V, испускаемые участками образца, содержащими двухслойную гетероструктуру WSe₂/MoSe₂ (слева), либо трехслойную структуру WSe₂/MoSe₂/WSe₂ (справа).
В двухслойной структуре виден эффект Штарка, обусловленный тем, что к энергии рекомбинации межслойного экситона добавляется энергия взаимодействия его дипольного момента с внешним полем. Влияние поля на спектр асимметрично: при одной полярности оно способствует рекомбинации, при другой – раздвигает электрон и дырку подальше, подавляя рекомбинацию.
В случае трехслойной структуры видна симметричная картина эффекта Штарка, потому что там образуются симметричные квадрупольные экситоны. Кроме того, интенсивность люминесценции вблизи V = 0 невелика из-за отсутствия у них дипольного момента. Но при больших по модулю V они разрываются на обычные межслойные экситоны.
#экситоны #дихалькогениды_переходных_металлов
В двухслойной структуре виден эффект Штарка, обусловленный тем, что к энергии рекомбинации межслойного экситона добавляется энергия взаимодействия его дипольного момента с внешним полем. Влияние поля на спектр асимметрично: при одной полярности оно способствует рекомбинации, при другой – раздвигает электрон и дырку подальше, подавляя рекомбинацию.
В случае трехслойной структуры видна симметричная картина эффекта Штарка, потому что там образуются симметричные квадрупольные экситоны. Кроме того, интенсивность люминесценции вблизи V = 0 невелика из-за отсутствия у них дипольного момента. Но при больших по модулю V они разрываются на обычные межслойные экситоны.
#экситоны #дихалькогениды_переходных_металлов
👍3
Большая и запутанная статья, в которой развивается теория мембраны запутанности (entanglement membrane). Она возникает при расчете наблюдаемых величин в квантовой системе, прошедшей через квантовую цепь, представляемой как сеть двухкубитных гейтов.
Матрица плотности системы после такого умножается с двух сторон на оператор унитарной эволюции U, а при расчете N-частичной корреляционной функции таких операторов будет 2N. Таким образом, нам нужно считать среднее <U⊗U⊗U…> тензорного произведения 2N операторов эволюции U. Если считать, что квантовая цепь случайна, то при усреднении по всевозможным U остаются лишь слагаемые, в которых двухкубитные гейты группируются по четности неких перестановок, связанных со спариванием операторов U.
Как показано на рисунке, группы «четных» и «нечетных» гейтов разделяются доменной стенкой, которая и называется мембраной запутанности. С величиной «поверхностного натяжения» этой мембраны связана скорость распространения возмущений по квантовой системе.
#квантовые_вычисления
Матрица плотности системы после такого умножается с двух сторон на оператор унитарной эволюции U, а при расчете N-частичной корреляционной функции таких операторов будет 2N. Таким образом, нам нужно считать среднее <U⊗U⊗U…> тензорного произведения 2N операторов эволюции U. Если считать, что квантовая цепь случайна, то при усреднении по всевозможным U остаются лишь слагаемые, в которых двухкубитные гейты группируются по четности неких перестановок, связанных со спариванием операторов U.
Как показано на рисунке, группы «четных» и «нечетных» гейтов разделяются доменной стенкой, которая и называется мембраной запутанности. С величиной «поверхностного натяжения» этой мембраны связана скорость распространения возмущений по квантовой системе.
#квантовые_вычисления
👍2😱1
Кстати говоря, концепция мембраны запутанности была придумана еще 5-6 лет назад, а статья из предыдущего поста посвящена, главным образом, следующему вопросу.
Четкое разделение двухкубитных гейтов на «четные» и «нечетные» возникает лишь при усреднении оператора эволюции U по всей мере Хаара. Если же эволюция квантовой системы является не полностью случайной, а какой-то конкретной, то усреднение по ансамблю U, строго говоря, проводить нельзя.
Авторы представляют неусредненный результат как усредненный плюс поправки. Последние приводят к тому, что некоторые двухкубитные гейты могут быть не четными либо нечетными, а третьего вида – «перпендикулярными». Такие перпендикулярные гейты образуют «наросты» на мембране запутанности, перенормирующие ее свойства. Таким образом, неусредненная по беспорядку (реализациям длинной и запутанной квантовой цепи) система качественно ведет себя как усредненная, но с перенормированными свойствами.
#квантовые_вычисления
Четкое разделение двухкубитных гейтов на «четные» и «нечетные» возникает лишь при усреднении оператора эволюции U по всей мере Хаара. Если же эволюция квантовой системы является не полностью случайной, а какой-то конкретной, то усреднение по ансамблю U, строго говоря, проводить нельзя.
Авторы представляют неусредненный результат как усредненный плюс поправки. Последние приводят к тому, что некоторые двухкубитные гейты могут быть не четными либо нечетными, а третьего вида – «перпендикулярными». Такие перпендикулярные гейты образуют «наросты» на мембране запутанности, перенормирующие ее свойства. Таким образом, неусредненная по беспорядку (реализациям длинной и запутанной квантовой цепи) система качественно ведет себя как усредненная, но с перенормированными свойствами.
#квантовые_вычисления
Загадочные каббалистические диаграммы из статьи о мембране запутанности.
#квантовые_вычисления #цитаты
#квантовые_вычисления #цитаты
Занятная работа: в ней на примере системы электронов, взаимодействующих с фононами, примесями и между собой, критически анализируются «общепринятые факты», касающиеся релаксации неравновесных многоэлектронных систем после накачки.
В частности, авторы рассматривают два расхожих утверждения:
(1) Скорость релаксации возбужденных квазичастиц дается их собственно-энергетической частью: τ⁻¹(ω) = –2 Im Σ(ω).
(2) При наличии нескольких каналов релаксации их скорости складываются: τ⁻¹ = (τ₁)⁻¹ + (τ₂)⁻¹ + …, это называют правилом Матиссена. Действительно, если возбужденное состояние может распадаться, к примеру, сразу по нескольким каналам, то динамика его населенности меняется согласно уравнению dn/dt = –n/ τ₁– n/ τ₂– … В итоге мы получаем экспоненциальную релаксацию n(t) ~ exp(–t/τ) с суммарной скоростью τ⁻¹.
В статье показывается, что на практике оба этих утверждения часто нарушаются. С первым тезисом проблема в том, что собственно-энергетическая часть Σ(ω), по-хорошему, описывает релаксацию одноэлектронной функции Грина G(t, t´) неравновесной системы как функцию относительного времени – разности ее аргументов t – t´. А такие наблюдаемые величины, как населенность возбужденных состояний, коэффициент отражения материала после накачки и другие, измеряются как функции времени задержки после накачки, то есть среднего времени (t + t´)/2. Таким образом, переносить релаксацию вдоль одной переменной на динамику вдоль другой переменной можно лишь с натяжкой.
Что касается второго тезиса, он противоречит часто наблюдаемым процессам мультиэкспоненциального распада: когда сначала наблюдаемая величина релаксирует быстро, с одним временем τ₁, потом спадает медленнее, с временем τ₂, потом может выявиться еще большее, третье время распада и т.д. Такое поведение – с разделением времен распада вместо их суммирования – не согласуется с правилом Матиссена и показывает, что уравнение для динамики распада должно иметь более сложный вид, чем показано выше.
Мультиэкспоненциальный распад требует наличия бутылочных горлышек, при которых разные каналы распада не идут одновременно с самого начала, а, к примеру, завершение одного канала распада является условием для начала второго. К примеру, термализация электронного газа после накачки, происходящая за счет электрон-электронных столкновений (первый, быстрый канал распада) должна завершиться для того, чтобы потом началось эффективное охлаждение электронов посредством испускания фононов (второй, более медленный канал).
#твердое_тело #открытые_квантовые_системы #фотоника
В частности, авторы рассматривают два расхожих утверждения:
(1) Скорость релаксации возбужденных квазичастиц дается их собственно-энергетической частью: τ⁻¹(ω) = –2 Im Σ(ω).
(2) При наличии нескольких каналов релаксации их скорости складываются: τ⁻¹ = (τ₁)⁻¹ + (τ₂)⁻¹ + …, это называют правилом Матиссена. Действительно, если возбужденное состояние может распадаться, к примеру, сразу по нескольким каналам, то динамика его населенности меняется согласно уравнению dn/dt = –n/ τ₁– n/ τ₂– … В итоге мы получаем экспоненциальную релаксацию n(t) ~ exp(–t/τ) с суммарной скоростью τ⁻¹.
В статье показывается, что на практике оба этих утверждения часто нарушаются. С первым тезисом проблема в том, что собственно-энергетическая часть Σ(ω), по-хорошему, описывает релаксацию одноэлектронной функции Грина G(t, t´) неравновесной системы как функцию относительного времени – разности ее аргументов t – t´. А такие наблюдаемые величины, как населенность возбужденных состояний, коэффициент отражения материала после накачки и другие, измеряются как функции времени задержки после накачки, то есть среднего времени (t + t´)/2. Таким образом, переносить релаксацию вдоль одной переменной на динамику вдоль другой переменной можно лишь с натяжкой.
Что касается второго тезиса, он противоречит часто наблюдаемым процессам мультиэкспоненциального распада: когда сначала наблюдаемая величина релаксирует быстро, с одним временем τ₁, потом спадает медленнее, с временем τ₂, потом может выявиться еще большее, третье время распада и т.д. Такое поведение – с разделением времен распада вместо их суммирования – не согласуется с правилом Матиссена и показывает, что уравнение для динамики распада должно иметь более сложный вид, чем показано выше.
Мультиэкспоненциальный распад требует наличия бутылочных горлышек, при которых разные каналы распада не идут одновременно с самого начала, а, к примеру, завершение одного канала распада является условием для начала второго. К примеру, термализация электронного газа после накачки, происходящая за счет электрон-электронных столкновений (первый, быстрый канал распада) должна завершиться для того, чтобы потом началось эффективное охлаждение электронов посредством испускания фононов (второй, более медленный канал).
#твердое_тело #открытые_квантовые_системы #фотоника
Physical Review X
General Principles for the Nonequilibrium Relaxation of Populations in Quantum Materials
Nonequilibrium experiments often lean on intuition from equilibrium physics, but that leads to misconceptions. A new analysis using many-body theory outlines a better approach to understanding these complex systems.
А вот поучительная иллюстрация из той же статьи, демонстрирующая релаксацию электронов после накачки под действием различных факторов. Это результат расчета распределения электронов по импульсам и энергии до прибытия импульса накачки (левый столбец диаграмм), во время накачки (центральный столбец) и спустя 86 фс после него (правый столбец).
При включении одного лишь электрон-фононного взаимодействия (первая строка диаграмм). Электроны могут отдать свою энергию фононам в области энергий шириной в две фононные частоты вокруг уровня Ферми. Как видно, в этой полосе эффективно идут процессы охлаждения.
Одно лишь рассеяние электронов на примесях (вторая строка) делает распределение изотропным, но не приводит к термализации по оси энергии в силу своей упругости.
В свою очередь, одно лишь электрон-электронное взаимодействие (третья строка) приводит к установлению теплового распределения Ферми-Дирака, но горячего, поскольку электронам некуда отдавать свою энергию.
#твердое_тело #открытые_квантовые_системы
При включении одного лишь электрон-фононного взаимодействия (первая строка диаграмм). Электроны могут отдать свою энергию фононам в области энергий шириной в две фононные частоты вокруг уровня Ферми. Как видно, в этой полосе эффективно идут процессы охлаждения.
Одно лишь рассеяние электронов на примесях (вторая строка) делает распределение изотропным, но не приводит к термализации по оси энергии в силу своей упругости.
В свою очередь, одно лишь электрон-электронное взаимодействие (третья строка) приводит к установлению теплового распределения Ферми-Дирака, но горячего, поскольку электронам некуда отдавать свою энергию.
#твердое_тело #открытые_квантовые_системы
👍1
Интересная работа о том, использует ли природа квантовые эффекты для увеличения эффективности фотосинтеза. А именно: является ли перенос энергии экситонами от места поглощения фотона к реакционному центру чисто квантовой последовательностью перескоков, чисто классической диффузией или же чем-то промежуточным?
Моделирование показывает, что при реалистичных условиях перенос происходит в промежуточном, частично когерентном режиме. Любопытно, что в этом режиме возбуждение распределено равномерно по всей цепочке переноса (ENAQT regime на рисунке) – вместо осцилляций в квантовом режиме или экспоненциального спадания в классическом режиме. Это делает эффективность переноса не только более высокой, но и весьма устойчивой к изменениям структуры молекулярного комплекса.
Хотя выигрыш в эффективности переноса здесь не так уж велик, чтобы служить движущей силой отбора. По-видимому, это либо случайное совпадение, либо результат приспособления к каким-то другим факторам отбора.
#биология #открытые_квантовые_системы
Моделирование показывает, что при реалистичных условиях перенос происходит в промежуточном, частично когерентном режиме. Любопытно, что в этом режиме возбуждение распределено равномерно по всей цепочке переноса (ENAQT regime на рисунке) – вместо осцилляций в квантовом режиме или экспоненциального спадания в классическом режиме. Это делает эффективность переноса не только более высокой, но и весьма устойчивой к изменениям структуры молекулярного комплекса.
Хотя выигрыш в эффективности переноса здесь не так уж велик, чтобы служить движущей силой отбора. По-видимому, это либо случайное совпадение, либо результат приспособления к каким-то другим факторам отбора.
#биология #открытые_квантовые_системы
Вот это чумовой эксперимент, в котором удалось наблюдать отклик WSe₂ на терагерцовые импульсы с разрешением до 0.3 фс, которое авторы назвали аттосекундным.
Идея метода показана на рисунке. Поле терагерцового импульса (c) разрывает экситон, имеющийся в многослойном WSe₂, на электрон и дырку – синий и красный шарики на панели (a). В системе покоя дырки электрон разгоняется полем сначала в одну сторону, потом обратно, пока не произойдет его обратное столкновение с дыркой. Излучение, испускаемое при этом столкновении, дает вклад в боковую полосу частот.
На панели (b) то же самое происходит в монослое WSe₂, где кулоновское притяжение электрона и дырки сильнее, из-за чего обратное столкновение происходит раньше. Сравнивая излучения в боковой полосе как функции времени в толстом материале и в монослое (d-e), можно видеть разность времен обратного столкновения – результат влияния многочастичных эффектов на динамику электронов и дырок – с разрешением меньше 1 фс.
#фотоника #дихалькогениды_переходных_металлов
Идея метода показана на рисунке. Поле терагерцового импульса (c) разрывает экситон, имеющийся в многослойном WSe₂, на электрон и дырку – синий и красный шарики на панели (a). В системе покоя дырки электрон разгоняется полем сначала в одну сторону, потом обратно, пока не произойдет его обратное столкновение с дыркой. Излучение, испускаемое при этом столкновении, дает вклад в боковую полосу частот.
На панели (b) то же самое происходит в монослое WSe₂, где кулоновское притяжение электрона и дырки сильнее, из-за чего обратное столкновение происходит раньше. Сравнивая излучения в боковой полосе как функции времени в толстом материале и в монослое (d-e), можно видеть разность времен обратного столкновения – результат влияния многочастичных эффектов на динамику электронов и дырок – с разрешением меньше 1 фс.
#фотоника #дихалькогениды_переходных_металлов
🔥1
Смотришь такой на модель, которую авторы теоретической работы обещают рассмотреть: куча электронов, между которыми имеется кулоновское отталкивание, а еще все эти электроны взаимодействуют с кучей мод квантованного электромагнитного поля (а значит, еще и дополнительно воздействуют друг на друга через запаздывающее поперечное поле), а еще включается член A² и противовращающие члены...
И думаешь: «ничего себе, какая амбициозная задача здесь ставится!» 😱
А потом авторы пишут: ну, для простоты кулоновское взаимодействие мы сейчас выключим, а для фотонов возьмем только одну моду с частотой ω, да и саму эту моду возьмем пространственно однородной...
И думаешь: «ну да, как всегда...» 😏
#электродинамика #цитаты
И думаешь: «ничего себе, какая амбициозная задача здесь ставится!» 😱
А потом авторы пишут: ну, для простоты кулоновское взаимодействие мы сейчас выключим, а для фотонов возьмем только одну моду с частотой ω, да и саму эту моду возьмем пространственно однородной...
И думаешь: «ну да, как всегда...» 😏
#электродинамика #цитаты
😁3
В этой работе рассмотрено, что происходит с двумерным электронным газом в резонаторе Фабри-Перо в режиме сильной связи – с «честным» учетом взаимодействия электронов с модами полости, включая член A².
Авторы показывают, что взаимодействие электронов с модами полости приводит к перенормировке их свойств: эффективная масса электронов повышается а в спектре проводимости появляются поляритонные резонансы, забирающие часть спектрального веса. Как результат, друдевский вес электронного газа уменьшается и при критической величине силы связи становится нулевым. При сверхкритической силе связи сфера Ферми электронного газа становится неустойчивой: вместо нее возникает что-то вроде уровней Ландау, но основного состояния у системы уже не существует.
Еще один интересный эффект – это превращение обычной, притягивающей силы Казимира между зеркалами полости в отталкивающую из-за наличия внутри электронного газа.
#электродинамика #фотоника
Авторы показывают, что взаимодействие электронов с модами полости приводит к перенормировке их свойств: эффективная масса электронов повышается а в спектре проводимости появляются поляритонные резонансы, забирающие часть спектрального веса. Как результат, друдевский вес электронного газа уменьшается и при критической величине силы связи становится нулевым. При сверхкритической силе связи сфера Ферми электронного газа становится неустойчивой: вместо нее возникает что-то вроде уровней Ландау, но основного состояния у системы уже не существует.
Еще один интересный эффект – это превращение обычной, притягивающей силы Казимира между зеркалами полости в отталкивающую из-за наличия внутри электронного газа.
#электродинамика #фотоника
Свежий обзор по квантовым батареям – устройствам хранения энергии, использующим эффекты квантовой когерентности и квантовой запутанности для получения превосходства над классическими системами в скорости зарядки и разрядки.
К примеру, классическая батарея, состоящая из N одинаковых частей, может заряжаться и разряжаться со скоростью, растущей пропорционально N (или еще медленнее), а квантовая батарея может делать это со скоростью ~N². Механизм, позволяющей квантовой батарее получать преимущество в скорости передачи энергии, схож со сверхизлучением Дике – когерентным взаимодействием множества кубитов с одной и той же электромагнитной модой, усиливающимся за счет конструктивной интерференции.
В обзоре подробно рассматриваются все теоретические аспекты устройства и работы квантовых батарей: хранение энергии и ее утечка, зарядка и разрядка, фундаментальные ограничения на их скорость, возможные реализации и т.д. А успешных экспериментов в этой области – пока что всего пара штук.
#квантовая_термодинамика
К примеру, классическая батарея, состоящая из N одинаковых частей, может заряжаться и разряжаться со скоростью, растущей пропорционально N (или еще медленнее), а квантовая батарея может делать это со скоростью ~N². Механизм, позволяющей квантовой батарее получать преимущество в скорости передачи энергии, схож со сверхизлучением Дике – когерентным взаимодействием множества кубитов с одной и той же электромагнитной модой, усиливающимся за счет конструктивной интерференции.
В обзоре подробно рассматриваются все теоретические аспекты устройства и работы квантовых батарей: хранение энергии и ее утечка, зарядка и разрядка, фундаментальные ограничения на их скорость, возможные реализации и т.д. А успешных экспериментов в этой области – пока что всего пара штук.
#квантовая_термодинамика
👍2