Недавно я писал о том, что наложение осциллирующей силы на одномерную решетку эффективно меняет интеграл перескока J как J → J₀(K/Ω)×J, где K и Ω – амплитуда и частота осциллирующей силы, J₀ – функция Бесселя нулевого порядка. Такой эффект был подтвержден в эксперименте с бозе-конденсатом атомов рубидия.
По тому, с какой скоростью атомное облако расползается с течением времени по оптической решетке, можно извлечь эффективный интеграл перескока J. На графике снизу он показан по модулю как функция параметра K₀ = K/Ω. Видно, что при K₀ ≈ 2.4 туннелирование между узлами решетки полностью подавляется, что можно считать примером динамической локализации.
На графиках справа показаны интерференционные картины от разлета атомов после выключения потенциала решетки. Как и должно быть, при J < 0 атомы в основном состоянии концентрируются вблизи квазиимпульса k = 0, а при J > 0 – вблизи краев зоны Бриллюэна k = ±π/a. Заодно видно, что между атомами в соседних узлах сохраняется взаимная когерентность.
#состояния_Флоке
По тому, с какой скоростью атомное облако расползается с течением времени по оптической решетке, можно извлечь эффективный интеграл перескока J. На графике снизу он показан по модулю как функция параметра K₀ = K/Ω. Видно, что при K₀ ≈ 2.4 туннелирование между узлами решетки полностью подавляется, что можно считать примером динамической локализации.
На графиках справа показаны интерференционные картины от разлета атомов после выключения потенциала решетки. Как и должно быть, при J < 0 атомы в основном состоянии концентрируются вблизи квазиимпульса k = 0, а при J > 0 – вблизи краев зоны Бриллюэна k = ±π/a. Заодно видно, что между атомами в соседних узлах сохраняется взаимная когерентность.
#состояния_Флоке
👍4
В этой работе продемонстрирован первый сверхпроводниковый квантовый компьютер с архитектурой фон Неймана. Он состоит из процессора и связанной с ним оперативной памяти. Правда, компьютер этот очень маленький: и процессор, и память содержат всего по два кубита (и еще в процессоре есть два регистра обнуления – кубита, которые используются для сброса других кубитов в состояние нуля). Тем не менее, он работает.
Смысл разделения квантового компьютера на процессор и память в том, что процессор состоит из «быстрых» кубитов, которые быстро переключаются, но плохо подходят для долговременного хранения квантовой информации, а память состоит из «медленных» кубитов – не столь быстро работающих, но обладающих большими временами когерентности.
На рисунке справа можно полюбоваться на результаты выполнения трехкубитной XOR-операции: состояние третьего кубита инвертируется (подвергается повороту на угол π), когда первый и второй кубиты в состояниях |ge> или |eg>, и остается прежним в других случаях.
#квантовые_вычисления
Смысл разделения квантового компьютера на процессор и память в том, что процессор состоит из «быстрых» кубитов, которые быстро переключаются, но плохо подходят для долговременного хранения квантовой информации, а память состоит из «медленных» кубитов – не столь быстро работающих, но обладающих большими временами когерентности.
На рисунке справа можно полюбоваться на результаты выполнения трехкубитной XOR-операции: состояние третьего кубита инвертируется (подвергается повороту на угол π), когда первый и второй кубиты в состояниях |ge> или |eg>, и остается прежним в других случаях.
#квантовые_вычисления
👍1
При помощи электрических цепей можно создавать аналоги кристаллических решеток, невозможных в нашем трехмерном евклидовом пространстве. Пример – двумерная решетка на гиперболической плоскости, обладающей постоянной отрицательной кривизной, которая состоит из правильных 8-угольников (на гиперболической плоскости возможны также решетки, состоящие из правильных 5- и 7-угольников).
В случае евклидовой квадратной решетки (A) периодичность решетки подразумевает отождествление 2 пар противоположных сторон ячейки. Как следствие, в координатном пространстве ячейка изоморфна двумерному тору (B), а кручение фаз по двум его замкнутым направлениям дает две компоненты квазиимпульса, заметающего первую зону Бриллюэна – также двумерный тор.
В случае гиперболической решетки отождествляются 4 пары противоположных сторон (C), элементарная ячейка имеет топологию поверхности с двумя отверстиями (D), а первая зона Бриллюэна представляет собой четырехмерный тор, так что квазиимпульс здесь 4-мерный.
#твердое_тело #отвал_башки
В случае евклидовой квадратной решетки (A) периодичность решетки подразумевает отождествление 2 пар противоположных сторон ячейки. Как следствие, в координатном пространстве ячейка изоморфна двумерному тору (B), а кручение фаз по двум его замкнутым направлениям дает две компоненты квазиимпульса, заметающего первую зону Бриллюэна – также двумерный тор.
В случае гиперболической решетки отождествляются 4 пары противоположных сторон (C), элементарная ячейка имеет топологию поверхности с двумя отверстиями (D), а первая зона Бриллюэна представляет собой четырехмерный тор, так что квазиимпульс здесь 4-мерный.
#твердое_тело #отвал_башки
🔥2❤1
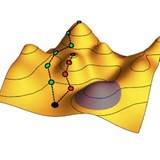
Кстати говоря, в статье из предыдущего поста впервые сформулировано обобщение теории Блоха для гиперболической плоскости. Статья довольно математизирована, но ее главная мысль в том, что на гиперболической плоскости квазиимпульс и первая зона Бриллюэна четырехмерны, хотя в координатном пространстве система двумерна.
На графике сверху показан пример зонной структуры частицы, движущейся по гиперболической плоскости в периодическом потенциале – зависимость уровней энергии частицы от квазиимпульса, движущегося в четырехмерном пространстве в направлении k ~ (0.8, 0.3, 1.2, 1.7). Для четырех состояний, показанных черными точками, диаграммы снизу показывают квадраты модуля волновой функции в пределах одной элементарной ячейки.
#твердое_тело
На графике сверху показан пример зонной структуры частицы, движущейся по гиперболической плоскости в периодическом потенциале – зависимость уровней энергии частицы от квазиимпульса, движущегося в четырехмерном пространстве в направлении k ~ (0.8, 0.3, 1.2, 1.7). Для четырех состояний, показанных черными точками, диаграммы снизу показывают квадраты модуля волновой функции в пределах одной элементарной ячейки.
#твердое_тело
И еще один занятный факт из той же статьи: на гиперболической плоскости даже в отсутствие потенциала, в случае свободного движения частицы, для волновой функции частицы не существует аналитического решения уравнения Шредингера. Но такое решение для неевклидового аналога плоской волны можно, конечно же, найти численно. Примеры решений показаны на рисунке: это квадраты модуля волновой функции на одной 8-угольной ячейке.
Верхняя строка диаграмм отвечает основному и трем возбужденным состояниям с периодическими граничными условиями, наложенными на 4 парах противоположных сторон ячейки. Иными словами, это случай квазиимпульса k = 0.
На нижней строке диаграмм k = (0.8, 0.3, 1.2, 1.7), то есть на 4 парах противоположных сторон на волновую функцию наложены скрученные граничные условия (twisted boundary conditions) с соответствующими фазами.
#твердое_тело #математика
Верхняя строка диаграмм отвечает основному и трем возбужденным состояниям с периодическими граничными условиями, наложенными на 4 парах противоположных сторон ячейки. Иными словами, это случай квазиимпульса k = 0.
На нижней строке диаграмм k = (0.8, 0.3, 1.2, 1.7), то есть на 4 парах противоположных сторон на волновую функцию наложены скрученные граничные условия (twisted boundary conditions) с соответствующими фазами.
#твердое_тело #математика
❤1
Бифенилен – это двумерный кристалл углерода с необычной решеткой, содержащей квадраты, шестиугольники и восьмиугольники атомов. Его электронные свойства существенно анизотропны: обе поверхности Ферми – электронная (вокруг точки S) и дырочная (вокруг точки Y) – имеют вытянутую форму. В среднем, скорость Ферми электронов в направлении оси x выше из-за более легких перескоков вдоль горизонтальных димеров.
В этом эксперименте при помощи спектроскопии энергетических потерь электронов были обнаружены анизотропные плазмоны, распространяющиеся вдоль поверхности бифенилена. Как показано на диаграмме в центре, дисперсия плазмонов в x-направлении (справа) идет гораздо круче, чем в y-направлении (слева). Кроме того, в x-направлении плазмоны существуют в широком диапазоне частот, от терагерцового до ультрафиолета. В y-направлении они ограничены лишь низкими частотами, а дальше быстро затухают, попадая в континуум. Занятно также, что у материала существует широкая область гиперболичности от 1 до 0.5 мкм.
#плазмоны
В этом эксперименте при помощи спектроскопии энергетических потерь электронов были обнаружены анизотропные плазмоны, распространяющиеся вдоль поверхности бифенилена. Как показано на диаграмме в центре, дисперсия плазмонов в x-направлении (справа) идет гораздо круче, чем в y-направлении (слева). Кроме того, в x-направлении плазмоны существуют в широком диапазоне частот, от терагерцового до ультрафиолета. В y-направлении они ограничены лишь низкими частотами, а дальше быстро затухают, попадая в континуум. Занятно также, что у материала существует широкая область гиперболичности от 1 до 0.5 мкм.
#плазмоны
👍1
Как учат еще на первом курсе любого физфака, при N-кратном повторении измерения относительная погрешность результата убывает как 1/√N. Можно ли сделать ошибку еще меньше, используя квантовое превосходство? Иными словами, обладает ли квантовая метрология преимуществом над классической? И если да, то в какой степени?
Ответы даются в этой работе. В классически-классической постановке (CC), когда несколько актов приготовления системы, проведения над ней унитарного преобразования Uᵩ и последующего измерения проводятся независимо N раз, ошибка ведет себя как 1/√N. Классически-квантовая постановка (CQ), подразумевающая квантовое измерение, проводимое совместно над N копиями системы, не дает никакого преимущества.
Меньшая ошибка, ведущая себя как 1/N, достигается лишь в квантово-классическом (QC) и квантово-квантовом (QQ) случаях. Таким образом, для уменьшения ошибки необходима квантовая запутанность исходного состояния системы, а скоррелированные измерения в конце – излишни.
#квантовая_механика #отвал_башки
Ответы даются в этой работе. В классически-классической постановке (CC), когда несколько актов приготовления системы, проведения над ней унитарного преобразования Uᵩ и последующего измерения проводятся независимо N раз, ошибка ведет себя как 1/√N. Классически-квантовая постановка (CQ), подразумевающая квантовое измерение, проводимое совместно над N копиями системы, не дает никакого преимущества.
Меньшая ошибка, ведущая себя как 1/N, достигается лишь в квантово-классическом (QC) и квантово-квантовом (QQ) случаях. Таким образом, для уменьшения ошибки необходима квантовая запутанность исходного состояния системы, а скоррелированные измерения в конце – излишни.
#квантовая_механика #отвал_башки
Ох уж эта бедная и несчастная традиционная неравновесная термодинамика!
Макроскопические флуктуационные теории несовместимы, гипотеза детального равновесия скомпрометирована, а концепция детального равновесия поставлена под угрозу! 😱
#цитаты #стохастическая_термодинамика
Макроскопические флуктуационные теории несовместимы, гипотеза детального равновесия скомпрометирована, а концепция детального равновесия поставлена под угрозу! 😱
#цитаты #стохастическая_термодинамика
😁2
В этой работе на 30 страницах формул (почти) из первых принципов выводятся эффективные уравнения неравновесной термодинамики.
Авторы отправляются от мезоскопической стохастической термодинамики – описания эволюции состояния системы как случайных перескоков между микро- или мезоскопическими состояниями (это, например, различные коллективные координаты молекул). Они, по мере увеличения масштабов рассматриваемых систем и процессов, группируются в локально равновесные макроскопические состояния (характеризуемые температурой, давлением и т.д.), поведение которых изучается уже неравновесной термодинамикой.
Ключевой математический аппарат, используемый при таком выводе – это теория больших отклонений. Она описывает концентрацию распределений вероятности при наборе большой статистики. Частный случай такой концентрации в форме гауссовой статистики описывается центральной предельной теоремой. Кстати говоря, именно такой случай подразумевается в традиционных флуктуационных теориях.
#стохастическая_термодинамика
Авторы отправляются от мезоскопической стохастической термодинамики – описания эволюции состояния системы как случайных перескоков между микро- или мезоскопическими состояниями (это, например, различные коллективные координаты молекул). Они, по мере увеличения масштабов рассматриваемых систем и процессов, группируются в локально равновесные макроскопические состояния (характеризуемые температурой, давлением и т.д.), поведение которых изучается уже неравновесной термодинамикой.
Ключевой математический аппарат, используемый при таком выводе – это теория больших отклонений. Она описывает концентрацию распределений вероятности при наборе большой статистики. Частный случай такой концентрации в форме гауссовой статистики описывается центральной предельной теоремой. Кстати говоря, именно такой случай подразумевается в традиционных флуктуационных теориях.
#стохастическая_термодинамика
❤4
«Это приближение часто используется, хотя оно и неправильно» – это из статьи из предыдущего поста.
#цитаты
#цитаты
😁5😱1
Классическая работа с выводом того, что сейчас называют формулой Онзагера-Мэчлапа. Эта формула дает вероятность того, что статистическая система, в ходе своей неравновесной динамики, пройдет по определенной траектории в пространстве параметров. К примеру, мы с течением времени увеличиваем давление на поршень в сосуде с газом и хотим понять, с какой вероятностью координата прошня пройдет по траектории x(t).
Среди всех траекторий, по которым может пойти система, есть наиболее вероятная – она дается обычной неравновесной термодинамикой. А есть флуктуации, вероятность которых гауссовым образом спадает при удалении от нее. Таким образом, вероятность траектории дается интегралом по путям. С современной точки зрения, формула Онзагера-Мэчлапа – это лишь гауссово приближение для флуктуаций, справедливо для достаточно больших систем и не очень сильных отклонений от равновесия.
А еще в этой работе был получен известный в неравновесной термодинамике принцип минимальной диссипации.
#стохастическая_термодинамика
Среди всех траекторий, по которым может пойти система, есть наиболее вероятная – она дается обычной неравновесной термодинамикой. А есть флуктуации, вероятность которых гауссовым образом спадает при удалении от нее. Таким образом, вероятность траектории дается интегралом по путям. С современной точки зрения, формула Онзагера-Мэчлапа – это лишь гауссово приближение для флуктуаций, справедливо для достаточно больших систем и не очень сильных отклонений от равновесия.
А еще в этой работе был получен известный в неравновесной термодинамике принцип минимальной диссипации.
#стохастическая_термодинамика
Исключительные точки – это точки в пространстве параметров неэрмитового гамильтониана, в которых происходит бифуркация его собственных значений. В этой работе было предсказано существование весьма странных исключительных связанных состояний вблизи таких точек.
Главная патология таких состояний в том, что числа их заполнения могут быть меньше 0 или больше 1. Как следствие, в таких системах может возникать отрицательная энтропия запутанности – нонсенс с точки зрения квантовой информатики. Наша интуиция, согласно которой число заполнения должно быть 0 или 1 (или в промежутке между 0 или 1 в случае статистического ансамбля), для неэрмитовых систем не работает из-за несохранения в них плотности вероятности.
Волновые функции таких состояний (жирные кривые на графике снизу) тоже ведут себя аномально по сравнению с другими собственными функциями гамильтониана (тонкими кривыми). Автор усматривает некую аналогию такого поведения с излучением Хокинга вблизи горизонта черной дыры.
#неэрмитовы_системы #отвал_башки
Главная патология таких состояний в том, что числа их заполнения могут быть меньше 0 или больше 1. Как следствие, в таких системах может возникать отрицательная энтропия запутанности – нонсенс с точки зрения квантовой информатики. Наша интуиция, согласно которой число заполнения должно быть 0 или 1 (или в промежутке между 0 или 1 в случае статистического ансамбля), для неэрмитовых систем не работает из-за несохранения в них плотности вероятности.
Волновые функции таких состояний (жирные кривые на графике снизу) тоже ведут себя аномально по сравнению с другими собственными функциями гамильтониана (тонкими кривыми). Автор усматривает некую аналогию такого поведения с излучением Хокинга вблизи горизонта черной дыры.
#неэрмитовы_системы #отвал_башки
👍2
А вот объяснение того, почему для исключительных связанных состояний числа их заполнения выходят за границы физически осмысленного интервала от 0 до 1.
Введем одночастичную матрицу плотности P(x,x´) = <c⁺(x)c(x´)>. Ее собственные значения дают числа заполнения одночастичных состояний, потому что после перевода в диагональный вид она будет выглядеть как <aᵤ⁺aᵥ> = fᵤδᵤᵥ, где aᵤ – операторы этих одночастичных состояний, fᵤ = 0, 1 – числа их заполнения.
Так и происходит в случае обычных квантовых состояний, заполненных ниже уровня Ферми (пример слева на рисунке). В случае же исключительных связанных состояний (справа на рисунке) матрица P(x,x´) сильно делокализована и имеет много больших матричных элементов вдали от диагонали. Причина этому – патологическое поведение их волновых функций и дефективность гамильтониана (его собственные векторы не образуют полного базиса) в исключительной точке. Собственные значения такой матрицы легко могут выходить за границы интервала от 0 до 1.
#неэрмитовы_системы #отвал_башки
Введем одночастичную матрицу плотности P(x,x´) = <c⁺(x)c(x´)>. Ее собственные значения дают числа заполнения одночастичных состояний, потому что после перевода в диагональный вид она будет выглядеть как <aᵤ⁺aᵥ> = fᵤδᵤᵥ, где aᵤ – операторы этих одночастичных состояний, fᵤ = 0, 1 – числа их заполнения.
Так и происходит в случае обычных квантовых состояний, заполненных ниже уровня Ферми (пример слева на рисунке). В случае же исключительных связанных состояний (справа на рисунке) матрица P(x,x´) сильно делокализована и имеет много больших матричных элементов вдали от диагонали. Причина этому – патологическое поведение их волновых функций и дефективность гамильтониана (его собственные векторы не образуют полного базиса) в исключительной точке. Собственные значения такой матрицы легко могут выходить за границы интервала от 0 до 1.
#неэрмитовы_системы #отвал_башки
Кстати говоря, в работе из предыдущего поста авторы утверждают, что впервые экспериментально наблюдали исключительные связанные состояния, реализовав их на базе электрических цепей.
Хотя это не совсем так: у них лапласиан электрической цепи (матрица, связывающая токи на узлах с напряжениями на различных участках) воспроизводит не гамильтониан той неэрмитовой системы, которую они моделируют, а лишь одночастичную матрицу плотности P(x,x´) этой системы, предварительно посчитанную вручную. На частотах, отвечающих собственным значениям такой матрицы, электрическая цепь дает резонансный отклик.
Как показано на графике, в эксперименте наблюдаются 4 резонанса, аналогичные набору чисел заполнения – вероятностей того, что заполнено «квантовое состояние» неэрмитовой системы. Два центральных резонанса отвечают нормальным числам заполнения 0 и 1, а два боковых – патологическим числам заполнения –1 и 2, характерным для исключительных связанных состояний.
#неэрмитовы_системы #отвал_башки
Хотя это не совсем так: у них лапласиан электрической цепи (матрица, связывающая токи на узлах с напряжениями на различных участках) воспроизводит не гамильтониан той неэрмитовой системы, которую они моделируют, а лишь одночастичную матрицу плотности P(x,x´) этой системы, предварительно посчитанную вручную. На частотах, отвечающих собственным значениям такой матрицы, электрическая цепь дает резонансный отклик.
Как показано на графике, в эксперименте наблюдаются 4 резонанса, аналогичные набору чисел заполнения – вероятностей того, что заполнено «квантовое состояние» неэрмитовой системы. Два центральных резонанса отвечают нормальным числам заполнения 0 и 1, а два боковых – патологическим числам заполнения –1 и 2, характерным для исключительных связанных состояний.
#неэрмитовы_системы #отвал_башки
👍2
Накачка Таулеса – перемещение целого числа частиц из одного места в другое при обходе гамильтониана вокруг особой точки в пространстве параметров – неоднократно наблюдалась на различных физических платформах. А в этом эксперименте реализована существенно многочастичная накачка Таулеса, требующая наличия межчастичного взаимодействия.
Здесь рассмотрена модель Райса-Меле для атомов (a): одномерная цепочка с чередующимися интегралами перескока, меньший из которых равен δ, и асимметрией Δ энергий соседних узлов. В отсутствие отталкивания на узле (U = 0) обход на плоскости (δ, Δ) вокруг начала координат – особой точки – сдвигает 2 частицы на одну элементарную ячейку (b). При U > 0 эта особая точка расщепляется на две, и обход вокруг каждой из них перемещает уже по 1 частице (c)-(e).
Как видно на графике для измеряемой скорости сдвига как функции U, накачка работает только при попадании особой точки вдоль контура обхода, при промежуточных значениях U.
#атомные_газы #топологические_материалы
Здесь рассмотрена модель Райса-Меле для атомов (a): одномерная цепочка с чередующимися интегралами перескока, меньший из которых равен δ, и асимметрией Δ энергий соседних узлов. В отсутствие отталкивания на узле (U = 0) обход на плоскости (δ, Δ) вокруг начала координат – особой точки – сдвигает 2 частицы на одну элементарную ячейку (b). При U > 0 эта особая точка расщепляется на две, и обход вокруг каждой из них перемещает уже по 1 частице (c)-(e).
Как видно на графике для измеряемой скорости сдвига как функции U, накачка работает только при попадании особой точки вдоль контура обхода, при промежуточных значениях U.
#атомные_газы #топологические_материалы
👍2
А вот как обход в пространстве параметров вокруг особой точки (накачка Таулеса из статьи из предыдущего поста) должен выглядеть в идеале и как его пришлось осуществлять в реальности.
#цитаты #топологические_материалы
#цитаты #топологические_материалы
Авторы этой работы утверждают, что наблюдали кристалл квадрупольных экситонов в трехслойной структуре WSe₂/MoSe₂/WSe₂. Фазовая диаграмма такой системы показана на рисунке на осях плотности экситонов n_ex и отношения неких характерных энергий R. При достаточно больших R, по мере увеличения n_ex, фаза кристалла квадрупольных экситонов сменяется фазой дипольных межслойных экситонов, располагающихся в шахматном порядке.
Квадрупольность экситонов здесь в том, что они составлены одним электроном в центре и дыркой, распределенной в виде двух «половинок» в верхнем и нижнем слоях. Такой комплекс не имеет электрического дипольного момента, поэтому его радиационная рекомбинация сильно подавляется.
Верхний график показывает, как, при повышении температуры выше 25 К, экситонный кристалл расплавляется, а нижний – как, при плотности экситонов выше 5×10¹¹ см⁻², он распадается на дипольные межслойные экситоны, что приводит к резкому увеличению коэффициента диффузии.
#экситоны #дихалькогениды_переходных_металлов
Квадрупольность экситонов здесь в том, что они составлены одним электроном в центре и дыркой, распределенной в виде двух «половинок» в верхнем и нижнем слоях. Такой комплекс не имеет электрического дипольного момента, поэтому его радиационная рекомбинация сильно подавляется.
Верхний график показывает, как, при повышении температуры выше 25 К, экситонный кристалл расплавляется, а нижний – как, при плотности экситонов выше 5×10¹¹ см⁻², он распадается на дипольные межслойные экситоны, что приводит к резкому увеличению коэффициента диффузии.
#экситоны #дихалькогениды_переходных_металлов
А вот еще красивые диаграммы из работы, где наблюдали кристалл квадрупольных экситонов. Это спектры люминесценции как функции вертикального электрического поля V, испускаемые участками образца, содержащими двухслойную гетероструктуру WSe₂/MoSe₂ (слева), либо трехслойную структуру WSe₂/MoSe₂/WSe₂ (справа).
В двухслойной структуре виден эффект Штарка, обусловленный тем, что к энергии рекомбинации межслойного экситона добавляется энергия взаимодействия его дипольного момента с внешним полем. Влияние поля на спектр асимметрично: при одной полярности оно способствует рекомбинации, при другой – раздвигает электрон и дырку подальше, подавляя рекомбинацию.
В случае трехслойной структуры видна симметричная картина эффекта Штарка, потому что там образуются симметричные квадрупольные экситоны. Кроме того, интенсивность люминесценции вблизи V = 0 невелика из-за отсутствия у них дипольного момента. Но при больших по модулю V они разрываются на обычные межслойные экситоны.
#экситоны #дихалькогениды_переходных_металлов
В двухслойной структуре виден эффект Штарка, обусловленный тем, что к энергии рекомбинации межслойного экситона добавляется энергия взаимодействия его дипольного момента с внешним полем. Влияние поля на спектр асимметрично: при одной полярности оно способствует рекомбинации, при другой – раздвигает электрон и дырку подальше, подавляя рекомбинацию.
В случае трехслойной структуры видна симметричная картина эффекта Штарка, потому что там образуются симметричные квадрупольные экситоны. Кроме того, интенсивность люминесценции вблизи V = 0 невелика из-за отсутствия у них дипольного момента. Но при больших по модулю V они разрываются на обычные межслойные экситоны.
#экситоны #дихалькогениды_переходных_металлов
👍3
Большая и запутанная статья, в которой развивается теория мембраны запутанности (entanglement membrane). Она возникает при расчете наблюдаемых величин в квантовой системе, прошедшей через квантовую цепь, представляемой как сеть двухкубитных гейтов.
Матрица плотности системы после такого умножается с двух сторон на оператор унитарной эволюции U, а при расчете N-частичной корреляционной функции таких операторов будет 2N. Таким образом, нам нужно считать среднее <U⊗U⊗U…> тензорного произведения 2N операторов эволюции U. Если считать, что квантовая цепь случайна, то при усреднении по всевозможным U остаются лишь слагаемые, в которых двухкубитные гейты группируются по четности неких перестановок, связанных со спариванием операторов U.
Как показано на рисунке, группы «четных» и «нечетных» гейтов разделяются доменной стенкой, которая и называется мембраной запутанности. С величиной «поверхностного натяжения» этой мембраны связана скорость распространения возмущений по квантовой системе.
#квантовые_вычисления
Матрица плотности системы после такого умножается с двух сторон на оператор унитарной эволюции U, а при расчете N-частичной корреляционной функции таких операторов будет 2N. Таким образом, нам нужно считать среднее <U⊗U⊗U…> тензорного произведения 2N операторов эволюции U. Если считать, что квантовая цепь случайна, то при усреднении по всевозможным U остаются лишь слагаемые, в которых двухкубитные гейты группируются по четности неких перестановок, связанных со спариванием операторов U.
Как показано на рисунке, группы «четных» и «нечетных» гейтов разделяются доменной стенкой, которая и называется мембраной запутанности. С величиной «поверхностного натяжения» этой мембраны связана скорость распространения возмущений по квантовой системе.
#квантовые_вычисления
👍2😱1