Эффект Хонга-У-Мандела – это двухфотонная интерференция, демонстрирующая бозонную статистику фотонов. Он состоит в том, что два фотона в совместном фоковском состоянии |1,1> (например, рожденные в нелинейно-оптическом кристалле), проходя через симметричный светоделитель, дают состояние (|2,0> + |0,2>)/√2. Получается, что в конце оба фотона попадают либо в верхний, либо в нижний детектор, то есть подвергаются группировке. Вероятность же одновременного срабатывания обоих детекторов должна быть, в идеале, равна нулю.

В этом эксперименте эффект Хонга-У-Мандела продемонстрирован для поверхностных плазмонов – то есть доказано, что они тоже являются бозонами. Два фотона падают на углы крестообразного металлического образца, возбуждая там поверхностные плазмоны, которые интерферируют в центре и высвечиваются с двух других углов. Как видно на графике, по мере приближения времени задержки Δt между двумя падающими фотонами к нулю вероятность одновременного срабатывания детекторов резко снижается.

#фотоника #плазмоны

В этой формуле из Википедии для гамильтониана взаимодействия двух магнитных диполей можно заметить загадочный контактный член, пропорциональный дельта-функции δ(r).

Откуда он берется? Как объясняется в этой статье Джексона, стандартная формула для диполь-дипольного взаимодействия (первое слагаемое) отталкивается от выражения для магнитного поля B(r) = [3ȓ(m•ȓ) – m]/r³, создаваемого диполем m, которое справедливо только на достаточно больших расстояниях r. Если представить магнитный диполь в виде петли или другого пространственного распределения тока в ограниченном объеме, то внутри этого объема такая формула уже неприменима.

Добавочное магнитное поле, имеющееся внутри диполя, интегрально по объему равно (8π/3)m, так что при малом размере диполя его можно эффективно сжать в точку в виде (8π/3)mδ(r). Таким образом, суммарное поле равно B(r) = [3ȓ(m•ȓ) – m]/r³ + (8π/3)mδ(r), а энергия второго диполя m´ в этом поле H ~ –(B•m´) дает финальное выражение с дельта-функционным членом.

#объяснения #электродинамика

Важная и широко цитируемая работа, в которой была рассмотрена топологическая классификация состояний кристаллов во внешнем периодическом поле (состояний Флоке-Блоха).

Эволюция волновой функции такой системы за один период ψ(t+T)=Uψ(t) описывается унитарным оператором Флоке U. Можно, в принципе, ввести эффективный гамильтониан U=exp(–iĤT/ℏ) и строить обычную топологическую классификацию, рассматривая спектр квазиэнергий гамильтониана Ĥ. Но здесь авторы показали, что во флоке-системах возможны принципиально новые фазы, обусловленные периодическим замыканием спектра квазиэнергий.

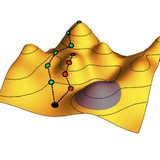
Даже если собственные состояния Ĥ образуют топологически тривиальные зоны, возможны состояния системы с киральными краевыми модами. На рисунке снизу показан пример того, как это возможно: поочередное усиление интегралов перескока в разных направлениях «протаскивает» за собой частицы по кругу. Эффект получается похожим на действие эффективного магнитного поля в топологическом изоляторе Черна.

#топологические_материалы #состояния_Флоке

Как я недавно писал, квантовая когерентность – то есть наличие недиагональных по энергиям элементов матрицы плотности – является ценным ресурсом, который можно использовать для реализации квантовых операций или извлечения работы из тепла. Она необходима даже для элементарного отсчета времени, потому что в отсутствие когерентностей любая квантовая система стационарна.

В этой работе доказывается, что невозможна полная очистка когерентности (coherence distillation). Это процесс, при котором на основе какого-то числа частично когерентных систем («зашумленных маятников» на рисунке сверху) создается полностью когерентное – то есть квантовомеханически чистое – состояние одной или нескольких систем («чистые маятники» снизу). При этом разрешено использовать внешние ресурсы, например, вспомогательные системы или работу, не обладающие собственной когерентностью.

Автор показывает, что, хотя полная очистка когерентности невозможна, частичную ее очистку производить можно.

#квантовые_вычисления #квантовая_термодинамика

Нет, сверху на рисунке не колобок и не смайлик, а всего лишь расчет эволюции двухкомпонентного бозе-конденсата, в котором создан вихревой диполь: два квантованных вихря противоположных знаков.

Авторы называют его Matryoshka-like density profile. С течением времени оба вихря выходят за границы атомного облака, оставляя в нем неоднородности – то есть начальная конфигурация нестабильна.

Снизу показан другой случай, который авторы называют bull’s eye profile.

#сверхтекучесть

Малоизвестный факт из квантовой механики: бывают потенциалы, в которых связанные состояния существуют в континууме, при энергиях выше порога ионизации. Такие потенциалы нарушают стандартную картину спектра «сначала идут дискретные связанные состояния, потом континуум свободно распространяющихся волн».

Одна из реализаций такого потенциала для электрона – это широкая квантовая яма, окруженная с двух сторон решетками в два раза более узких ям. На энергии, при которой центральная яма оказывается шириной в половину длины волны, а узкие ямы и промежутки между ними – в четверть длины волны, возникнет связанное состояние.

Формирование такого состояния можно интерпретировать либо как стоячую волну между двумя брэгговскими зеркалами, либо как связанное состояние на дефекте в кристалле-сверхрешетке. В этом эксперименте 1992 года наблюдался оптический переход между обычным связанным состоянием в широкой яме и связанным состоянием в континууме в гетероструктурах AlInAs/GaInAs.

#квантовая_механика

Механизм внимания (attention), используемый в нейронных сетях архитектуры «трансформер», произвел настоящую революцию в работе с текстовыми данными и привел к созданию ChatGPT. Вот одна из первых работ, в которой механизм внимания был использован для улучшения качества машинного перевода. Здесь я постараюсь наиболее понятно рассказать, как он устроен и работает.

Первые нейронные сети, переводящие тексты с одного языка на другой, были созданы в 2013-2014 годах. Они были устроены в виде автокодировщика: нескольких слоев нейронов (кодировщика), сжимающих последовательность слов на одном языке в вектор контекста, и нескольких слоев нейронов (декодировщика), превращающих вектор контекста в последовательность слов на другом языке. Вектор контекста содержит информацию о смысле предложения, выраженную не на человеческом, а на машинном языке, понятном лишь самой нейросети.

При генерации вектора контекста принимается во внимание последовательный характер предложения, то есть зависимость смысла каждого слова от предшествующих слов в предложении. Поэтому выглядит она так: для каждого слова xᵢ входного предложения (определенным образом оцифрованного, то есть превращенного в вектор) генерируется вектор аннотации hᵢ = f(xᵢ, hᵢ₋₁), где f – обучаемая нелинейная функция, реализуемая пропусканием аргументов через несколько слоев нейронов. Как видно, аннотация i-го слова зависит не только от самого этого слова, но и от аннотации (i–1)-го слова. Это заставляет кодировщик, при попытке извлечь смысл каждого слова, учитывать смысл предыдущих слов.

После прохода через все предложение на основе всех аннотаций генерируется вектор контекста c = q(h₁, h₂, …), где q – еще одна обучаемая нелинейная функция. Декодировщик вычисляет вероятность того, что i-е слово переведенного предложения должно быть yᵢ, также последовательно: p(yᵢ) = g(yᵢ₋₁, sᵢ, c). Как видно, эта вероятность зависит от предыдущего слова yᵢ₋₁, вектора контекста c и от вектора текущего состояния декодировщика sᵢ, которое также последовательно обновляется с учетом предыдущего состояния, предыдущего слова и контекста: sᵢ = r(sᵢ₋₁, yᵢ₋₁, c). Произведение вероятностей p(y₁)p(y₂)… дает меру правдоподобия каждого варианта y₁y₂… всего переведенного предложения, так что остается лишь выбрать тот вариант, для которого произведение максимально.

Примерно так были устроены первые нейросетевые модели машинного перевода. Они использовали вектор контекста c фиксированной длины, так что качество перевода длинных предложений снижалось из-за невозможности вместить в этот вектор весь их смысл. Новшество этой работы в том, что при генерации переведенного предложения для каждого его слова используется свой вектор контекста cᵢ, то есть формулы выше нужно изменить на p(yᵢ) = g(yᵢ₋₁, sᵢ, cᵢ) и sᵢ = r(sᵢ₋₁, yᵢ₋₁, cᵢ).

А самое важное – как эти векторы контекста cᵢ получаются. Они вычисляются как взвешенная сумма cᵢ = Σᵤ αᵢᵤhᵤ аннотаций к словам входного предложения с коэффициентами αᵢᵤ. Каждый такой коэффициент пропорционален экспоненте степени совмещения eᵢᵤ (alignment) i-го переведенного слова с u-м словом исходного предложения, а сумма коэффициентов нормируется на единицу. Иными словами, αᵢᵤ = exp(eᵢᵤ)/Σᵥ exp(eᵢᵥ). Из этой формулы видно, что αᵢᵤ вычисляется как мягкий максимум (softmax) среди всех eᵢᵤ. Степень совмещения eᵢᵤ = a(sᵢ₋₁, hᵤ) считается на основе комбинаций скрытого состояния декодировщика sᵢ₋₁ и аннотации hᵤ входного слова, то есть на основе пары понятных машине локальных «смыслов» i-го переведенного и u-го входного слов. Функция a также обучается умению правильно сопоставлять эти смыслы.

Таким образом, при принятии решения о том, какое из переведенных слов лучше всего подходит, модель принимает во внимание все слова исходного предложения, но не в равной степени. Она обращает внимание лишь на определенные слова исходного предложения, которые наиболее сильно согласуются по смыслу с тем новым словом перевода, которое сейчас нужно подобрать. Механизм внимания «подсвечивает» определенные фрагменты входных данных, снимая ограничение на их объем.

#нейронные_сети #популярное

А вот иллюстрация к предыдущему посту, показывающая наглядно, как работает механизм внимания при машинном переводе. Авторы тестировали свою модель на переводе предложений с английского языка на французский. На рисунке показаны матрицы степеней соответствия eᵢᵤ между словами исходного предложения (столбцы) и словами переведенного предложения (строки). Они показывают, насколько сильное внимание нужно обратить при подборе каждого переведенного слова на различные слова оригинала.

Слева видна интересная антидиагональная структура, возникшая из-за обращения порядка слов при переводе European Economic Area на французский как zone économique européen.

Справа видно, что возникает при переводе the man как l’ homme. При выборе артикля l’ нейросеть больше всего внимания обращает не на его дословный аналог the в исходном предложении, а на последующее слово man – потому что во французском языке артикль зависит от рода, числа и первой буквы последующего слова.

#нейронные_сети #популярное

Свежий эксперимент с наблюдением жидкости Латинджера в скрученном бислое двумерного дихалькогенида переходных металлов WTe₂. Это экзотическая фаза, возникающая в одномерной системе взаимодействующих электронов, в которой обычные электронные и дырочные возбуждения пропадают, а их место занимают существенно коллективные плазмоны и спиноны.

Муаров узор, получающийся при скручивании WTe₂ на небольшой угол, оказывается не треугольным (как обычно), а состоящим из одномерных цепочек. Перескоки электронов вдоль цепочки гораздо сильнее, чем между цепочками, что дает начало массиву почти независимых квантовых нитей.

Физика латенждеровской жидкости проявляется, например, в том, что дифференциальная туннельная проводимость dI/dV между нитями зависит от температуры и напряжения степенным образом: dI/dV ~ T^α, V^α, где α ≈ 1.53. Это следствие подавления плотности состояний квазичастиц вблизи уровня Ферми. На графике видно, как все зависимости (dI/dV)/T^α схлопываются в одну кривую.

#дихалькогениды_переходных_металлов

Гидродинамическая генерация спина – это появление спиновой поляризации в жидкости, течение которой обладает завихренностью. Как показано на схеме слева, при вязком течении в трубке возникают поперечный градиент скорости v и завихренность ω = rot v. Из-за гиромагнитной связи вращение жидкости дает спиновую поляризацию s ~ ω, которая, будучи пространственно неоднородной, выравнивается посредством диффузионных спиновых токов jˢ ~ ∇s.

В этом эксперименте была зарегистрирована сильная генерация спина при протекании ртути через тонкие капилляры. Спиновые токи, направленные от стенок капилляра к центру, приводят, за счет имеющегося в ртути обратного спинового эффекта Холла, к генерации разности потенциалов V_e вдоль оси.

Как показано на схеме и графиках, при ламинарном течении, когда скорость потока пропорциональна перепаду давлений v ~ P, градиент скорости равномерно распределен по сечению. При турбулентном течении v ~ √P, градиент сосредоточен вблизи стенок и эффективность генерации снижается.

#гидродинамика

Занятная идея спаривания безмассовых дираковских электронов, происходящего в некотором диапазоне энергий симметрично вокруг дираковской точки, но над уровнем Ферми.

Такое спаривание не должно приводить к появлению щели в спектре, как в сверхпроводнике или экситонном диэлектрике. Авторы предполагают, что коэффициенты преобразований Боголюбова u и v, определяющие структуру спаривания, по всему протяжению слоя спаривания близки к u = v = 1/√2. Это означает, что электронные состояния в среднем заполнены на 1/2.

Таким образом, ниже области спаривания (сплошная синяя область) электронные состояния заняты полностью, а в самой области спаривания вблизи дираковской точки (заштрихованная синяя область) они заняты наполовину и скоррелированы. Общее число электронов выходит такое же, как если бы уровень Ферми находится ровно в дираковской точке.

Авторы назвали область спаривания ферми-льдом, «парящим» над морем Ферми – по аналогии с обычным льдом, который плавает на поверхности воды.

#графен #сверхпроводимость

Эффект Ааронова-Бома заключается в том, что волновая функция заряженной частицы, обходящей вокруг соленоида с магнитным потоком, приобретает нетривиальную фазу. Или, что то же самое, два фрагмента волнового фронта, обходящие соленоид слева и справа, приобретают разность фаз, которую можно обнаружить интерференционными измерениями.

При этом предполагается, что сама частица не попадает в область магнитного поля внутри соленоида. С классической точки зрения, она не подвергается действию силы Лоренца и поэтому не должна никак «чувствовать» наличие магнитного потока. Но в квантовой механике это не так: наличие магнитного поля внутри соленоида влияет на квантовое состояние частицы, обходящей вокруг него.

В обоих случаях приобретаемая фаза (или разность фаз) равна φ = (e/ℏc)∮A•dl = eΦ/ℏc, где циркуляция векторного потенциала A берется по замкнутому контуру, обходящему вокруг соленоида. При помощи теоремы Стокса ее можно связать с потоком Φ магнитного поля B = rot A через соленоид. Хотя сам векторный потенциал ненаблюдаем и зависит от калибровки, его циркуляция по замкнутому контуру (как и магнитный поток) калибровочно инвариантна и наблюдаема. Таким образом, и фаза φ тоже наблюдаема, но для ее наблюдения требуется, тем или иным образом, замыкать контур обхода вокруг соленоида.

В этой странной статье в Physical Review Letters утверждается, что фаза, приобретаемая волновой функцией частицы при движении вокруг соленоида, наблюдаема и не зависит от калибровки даже без замыкания траектории. К примеру, если частица начнет обходить соленоид слева и пройдет 1/4 дуги, то фаза ее волновой функции, приобретенная в ходе такого незавершенного обхода, может быть однозначно вычислена и измерена. Авторы отталкиваются от рассмотрения частицы как квантовой системы, соленоида – как классической системы, а взаимодействие частицы с соленоидом рассматривается посредством квантованного электромагнитного поля.

При этом авторы сначала берут кулоновскую калибровку, а потом заявляют: «мы получили калибровочно инвариантный результат». Звучит забавно – калибровочно инвариантный результат, полученный в кулоновской калибровке. У них выходит некое выражение для фазы, связанное с энергией электромагнитного взаимодействия частицы с соленоидом, и при этом имеющее противоположные знаки при нахождении частицы слева или справа.

Также авторы предлагают измерить разность фаз, приобретаемую частицей при обходе соленоида слева или справа, без завершения этого обхода – если и слева, и справа частица пройдет лишь часть пути. Для этого частицу можно реализовать в виде кубита, переменная σ_z которого задает нахождение слева (σ_z = +1) или справа (σ_z = –1) от соленоида. Тогда измерение фазы волновой функции кубита, приведенного в состояние суперпозиции (|+1> + |–1>)/√2 и во взаимодействие с соленоидом, даст калибровочно инвариантную разность фаз, приобретенную при незавершенном обходе.

С моей точки зрения, проблема здесь в том, что само техническое устройство кубита предполагает определенную калибровку относительной фазы между состояниями |+1> («слева от соленоида») и |–1> («справа от соленоида»). Эта калибровка уже определенным образом соотносит между собой фазы частицы в двух пространственно удаленных точках и, тем самым, эффективно замыкает путь обхода. Таким образом, предлагаемая авторами методика и правда дает возможность измерить калибровочно инвариантную разность фаз, но обход вокруг соленоида здесь на самом деле замкнут. Так что измерение калибровочно инвариантной фазы Ааронова-Бома вдоль незамкнутого участка траектории все-таки оказывается невозможным.

#квантовая_механика #электродинамика #топологические_материалы

Хиггсовская мода в сверхпроводнике – это колебание модуля параметра порядка, то есть амплитуды сверхпроводящей щели. В отличие от колебаний фазы параметра порядка, которые сопровождаются колебаниями плотности и срастаются с плазмоном, хиггсовскую моду тяжело наблюдать, поскольку в приближении линейного отклика она почти не взаимодействует с электромагнитным полем.

Однако взаимодействие подавлено лишь в пределе q → 0, а при ненулевых волновых векторах q взаимодействие существует. В этой теоретической работе предлагается связывать хиггсовскую моду с плазмонами, возникающими в графене, расположенном над поверхностью сверхпроводника на небольшом расстоянии. Из-за комбинации графена и металлического сверхпроводника плазмоны получаются с довольно низкой акустической дисперсией, что дает доступ к большим q при небольших частотах.

На диаграмме снизу показан пример антипересечения дисперсий за счет гибридизации акустического плазмона и хиггсовской моды, имеющей небольшую энергию 2Δ.

#сверхпроводимость #плазмоны

Допированный калием фулеренный кристалл K₃C₆₀ – интересный материал, демонстрирующий сверхпроводимость при 20 К. Но знаменит он тем, что при облучении инфракрасным светом его сверхпроводимость усиливается.

В этом эксперименте продемонстрировано, что сверхпроводимость в K₃C₆₀ после лазерного импульса держится несколько наносекунд – огромное время по меркам твердотельных процессов – и существует при комнатной температуре. На графиках справа видно, как, спустя 50 пс после лазерной накачки, ведут себя коэффициент отражения, и вещественная σ₁ и мнимая σ₂ части оптической проводимости. По сравнению с тем, что было до накачки (красной кривой), видны признаки сверхпроводимости: повышения коэффициента отражения до 1, подавление поглощения σ₁ и расходящийся диамагнитный отклик σ₂ ~ 1/ω при частотах внутри щели.

Как показано снизу, наибольший эффект достигается при накачке на энергии 41 мэВ. Предполагается, что это происходит из-за попадания в резонанс то ли с фононной, то ли с экситонной модой.

#сверхпроводимость

Поскольку сегодня в этом телеграм-канале день сверхпроводимости, приведу еще полезный факт из статьи из предыдущего поста.

Оптическая проводимость σ(ω) сверхпроводника (а следовательно, и его диэлектрическая функция, коэффициент отражения и т.д.) при низких частотах хорошо описывается двухжидкостной моделью. Как показано формулой на рисунке, первая ее часть – это друдевская проводимость сверхпроводящей компоненты с нулевым затуханием, дающая вклад ~δ(ω) в вещественную часть и идеальный диамагнитный вклад ~1/ω в мнимую часть. Она пропорциональна плотности сверхтекучей компоненты Λₛ. Вторая часть – это друдевская проводимость нормальной компоненты, пропорциональная ее плотности Λₙ и обладающая затуханием. Еще авторы добавили два лоренциана при более высоких частотах (последнее слагаемое в формуле).

Графики показывают результаты фитирования двухжидкостной моделью проводимости в нормальном состоянии при условии Λₛ=0 (черный пунктир) и в сверхпроводящем состоянии с Λₛ>0 (голубая кривая).

#сверхпроводимость

Сейчас все обсуждают соединение LK-99, вроде как, демонстрирующее сверхпроводимость и магнитную левитацию при комнатной температуре. В этой работе оперативно провели DFT-расчеты его электронных свойств. Предварительные результаты оказались любопытными: LK-99 является металлом, причем с почти вырожденными по энергии ферро- и антиферромагнитной фазами. А еще у него обнаруживаются почти плоские энергетические зоны и какое-то невероятно сильное электрон-фононное взаимодействие.

Состав LK-99 выражается приблизительной формулой Pb₉Cu(PO₄)₆O. Расчет зонной структуры в ферромагнитном основном состоянии, представленный сверху, показывает, что пересекающая уровень Ферми энергетическая зона почти плоская и составлена d-орбиталями атомов меди.

А диаграмма снизу показывает, как меняется зонная структура при небольшом смещении атомов за счет фононного колебания: материал внезапно превращается в изолятор. Авторы пишут, что они в первый раз видят, чтобы фононы так сильно влияли на зонную структуру.

#сверхпроводимость

А вот еще вчерашний препринт от китайских исследователей, которым также удалось синтезировать высокотемпературный сверхпроводник LK-99. Непонятно, получилось ли у них такое же соединение, как у авторов оригинального открытия, где сверхпроводимость была при комнатной температуре, или что-то близкое по составу.

По крайней мере, здесь наблюдается сверхпроводимость при температуре 100 К. Таким образом, даже безотносительно комнатнотемпературной сверхпроводимости, LK-99 очень интересен как представитель нового семейства высокотемпературных сверхпроводников.

#сверхпроводимость

Познавательная и отлично написанная статья о возможности локализации «волновой функции» фотона в пространстве.

Квантуя электромагнитное поле, автор рассматривает однофотонные состояния и ищет ответ на вопрос о том, насколько сильно могут быть сосредоточены в пространстве характерные для них функции: плотности энергии электромагнитного поля и вероятности обнаружения фотона. Оказывается, что с увеличением расстояния от центра r обе этих функции могут убывать в пространстве как чуть-чуть растянутая экспонента exp{–(r/a)ᵞ}, где γ меньше единицы, но, в принципе, может быть сколь угодно к ней близка.

Таким образом, все наблюдаемые величины в однофотонном состоянии могут спадать в пространстве почти экспоненциально. Конечно, это может происходить лишь в определенный момент времени, потому что при дальнейшей эволюции все расплывется. Кстати говоря, в многофотонных состояниях – например, когерентным – все эти функции могут не просто экспоненциально убывать, а быть строго ограничены конечной областью пространства.

#фотоника

Оказывается, производная решения уравнений Максвелла тоже является решением уравнений Максвелла 😱.

А еще окончание цитаты крутое.

#электродинамика #цитаты

В спиновом льде возможно образование возбуждений, при которых электронные спины (большинство, 3 из 4) расходятся «ежиком» во все стороны (S) или наоборот, сходятся к центру (N). Примеры таких возбуждений показаны на рисунке слева, и по свойствам они во многом похожи на магнитные монополи.

В этом эксперименте был косвенно зарегистрирован ток магнитных монополей под действием внешнего магнитного поля. По аналогии с электричеством – движением электрических зарядов в электрическом поле – авторы называют его «магнетричеством».

Достаточно сильное магнитное поле должно приводить к диссоциации связанных пар монополей и усилению «магнитной проводимости». Это аналог второго эффекта Вина – увеличения проводимости электролита в сильном электрическом поле. Здесь вместо проводимости регистрируется пропорциональная ей величина – скорость релаксации мюонного спина λ, возрастающая в магнитном поле. По скорости ее роста авторы определили величину магнитного заряда Q как функцию температуры.

#стекла #твердое_тело

А вот еще один препринт по комнатнотемпературной сверхпроводимости, вышедший в пятницу. Исследователи из Уханя тоже синтезировали LK-99, и он у них левитирует над магнитом даже лучше, чем у первооткрывателей.

Точнее, не совсем левитирует, а просто встает стоймя при поднесении магнита снизу, но под большим углом – почти вертикально. А у первооткрывателей он лишь немного приподнимался. Вот здесь можно посмотреть на соответствующее видео.