Для определения степени запутанности двух квантовых систем нужно, по-хорошему, полностью измерить их совместную матрицу плотности, а потом еще и провести расчеты, экспоненциально усложняющиеся с ростом размера системы. Поэтому задачу упрощают, используя индикаторы запутанности (entanglement witnesses) – величины, которые относительно легко измеряются и при этом дают для степени запутанности оценку снизу.

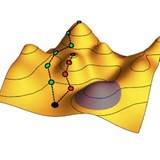
В этом эксперименте был использован новый индикатор запутанности, основанный на совместной статистике нескольких переменных X_a, X_b, K_a, K_b. Это могут быть, как в данном случае, распределение координат и волновых векторов по осям (x, y) двух запутанных фотонов. Адаптивный алгоритм сам определяет, в каком месте с каким разрешением их измерять.

В результате удалось довольно быстро измерить запутанность в пространстве размерности 512⁴ (более 68 миллиардов) – это в 10¹⁸ быстрее, чем напрямую, при помощи томографии матрицы плотности.

#квантовая_механика #квантовые_вычисления

Кстати говоря, степень квантовой запутанности двух фотонов, измеренная в работе из предыдущего поста, составляет 7.11 бита, как показано оранжевой кривой. Точнее, она измеряется в ебитах (ebits, entanglement bits).

Не знаю как сейчас, но на момент публикации в 2019 году это была самая большая по величине запутанность, когда-либо измеренная между любыми двумя квантовыми системами.

#квантовая_механика #квантовые_вычисления

Очередная работа из серии «мы реализовали в эксперименте простейшую квантовую систему с 2-3 энергетическими уровнями и убедились, что квантовая механика таки работает».

В этот раз при помощи атомов в оптических ловушках реализовали хаббардовский димер – две отталкивающиеся частицы со спином 1/2 в двух соседних потенциальных ямах. Это элементарный строительный блок модели Хаббарда, используемой для описания сильно-коррелированных систем и, в частности, высокотемпературных сверхпроводников.

На графике сверху показано как должны себя вести 4 энергетических уровня димера при изменении взаимодействия атомов на узле U. При U→+∞ состояния |LL> и |RR> с двойными заполнениями левой либо правой ямы выталкиваются вверх. Как видно на графиках снизу, в основном состоянии при этом обе частицы предпочитают распределяться по разным ямам, а в высоко возбужденном – находятся в одной яме. Измеренные вероятности (точки) согласуются с предсказаниями квантовой механики (линиями).

#квантовая_механика #сильные_корреляции

Встречайте Imagen – новую нейросеть, генерирующую фотореалистичные изображения по словесным описаниям. В статье можно найти красивые примеры ее работы.

На рисунке описана ее архитектура. Текстовое описание поступает в языковую модель – нейросеть архитектуры T5-XXL (это трансформер, как и знаменитый ChatGPT), которая обучается на корпусе текстов и умеет выделять сжатые представления фраз (embeddings). Они подаются на три последовательных каскада диффузионных моделей: используя метод обратной диффузии, эти модели превращают случайный шум в осмысленное изображение.

Принцип работы такого метода я описывал в отдельной статье. При этом диффузия определенным образом «направляется» как сжатым представлением текстовой фразы, так и более грубыми изображениями с предыдущего каскада.

Авторы используют ряд тестов (в том числе с использованием оценок людей), демонстрирующих, что Imagen по всем параметрам превосходит нейросети-конкуренты: DALL-E 2, GLIDE, VQ-GAN+CLIP и Latent Diffusion.

#нейронные_сети #популярное

Вот несколько примеров работы нейросети Imagen: изображения вместе с текстовыми описаниями, по которым они сгенерированы. 👇

А вот еще любопытный пример из статьи, демонстрирующий, что нейронная сеть, как правило, может выдавать лишь вариации того, на чем ее обучали.

Сверху нейросети Imagen и DALL-E 2 просят нарисовать лошадь, едущую на астронавте. Но они, будучи обучены на картинках, где люди ездят на лошадях, а не наоборот, выдают вместо этого изображения с астронавтом, едущим на лошади.

Однако снизу нейросети Imagen иногда удается нарисовать панду, создающую латте-арт (как и требуется), вместо более «привычного» латте-арта в виде панды, в которое генерация скатывается в большинстве случаев.

#нейронные_сети #популярное

По двухпроводной линии можно запустить электромагнитную волну с заданными профилями напряжения V(t) и тока I(t). Авторы этой статьи задались вопросом: каким фотонным состоянием описывается такая волна и как распределена по пространству «волновая функция» этого фотона?

Для этого авторы выразили оператор рождения фотона b⁺ через операторы плотностей заряда Q(x) и магнитного потока Φ(x), входящими в оператор с амплитудами θ_q(x) и θ_φ(x). Эти амплитуды, являющиеся ближайшими аналогами волновой функции, но для фотона, выражаются через V(t) и I(t) при помощи преобразований Гильберта H_x – таких же интегральных преобразований, которые встречаются, к примеру, в соотношениях Крамерса-Кронига.

Следует помнить, что преобразования Гильберта нелокальны, из-за чего и фотон всегда делокализован. На графиках показан пример: слева профиль импульса V(x), а справа – его преобразование Гильберта, входящее в формулы для амплитуд.

#фотоника #электродинамика

А вот еще интересные следствия формул, полученных авторами в статье из предыдущего поста.

Из-за преобразований Гильберта «волновая функция» фотона всегда выходит за пределы самого импульса – его профилей напряжения V(t) и тока I(t). Если импульс является биполярным, то есть ∫I(t)dt = 0, то среднее число фотонов в импульсе конечно. Аккуратным ослаблением импульса можно довести число фотонов до единиц, используя такие импульсы в квантовой криптографии.

Если же импульс униполярный, ∫I(t)dt ≠ 0, то среднее число фотонов в нем расходится! Такой импульс всегда будет уязвим для атак: его можно детектировать, поглощая часть фотонов, и потом усиливать для компенсации, так что перехват импульса будет незаметен.

Любопытна ситуация двух противоположных униполярных импульсов: число фотонов здесь расходится при увеличении расстояния между ними. С точки зрения числа фотонов (квантовой), такой сигнал может быть очень «ярким», будучи при этом «тусклым» по меркам классической амплитуды тока.

#фотоника #электродинамика

Вот пример расчетов зонной структуры кремния на квантовом компьютере, состоящим всего из двух (!) кубитов. Их результаты показаны синими точками.

Казалось бы, как можно настолько точно посчитать зонную структуру всего двумя кубитами, если на классическом компьютере для этого нужны куча данных о кристалле и структуре атомов кремния, сложные квантовомеханические приближения (типа метода функционала плотности или связанных кластеров), возня с базисами и так далее?

Секрет в том, чтобы для этих двух кубитов правильно подобрать подогнать гамильтониан, диагонализация которого сразу даст правильный ответ. Прямо как в анекдоте про Капицу, который заработал 999 долларов за то, что «знал, куда ударить».

#квантовые_вычисления #твердое_тело

Что будет, если поместить двумерную систему в чисто мнимое магнитное поле? Если вещественный векторный потенциал, согласно подстановке Пайерлса, модулирует фазу интегралов перескока между узлами решетки, то чисто мнимый векторный потенциал модулирует их амплитуды, так что система становится неэрмитовой.

Тонкий момент здесь – зависимость получающихся волновых функций и уровней энергии от калибровки мнимого векторного потенциала. При смене калибровке волновая функция вместо обычных калибровочных преобразований ψ→exp(iθ)ψ подвергается преобразованиям подобия ψ→exp(θ)ψ. Спектр энергий гамильтониана при этом сохраняется, так что для мнимых магнитных полей существует свой аналог калибровочной инвариантности.

Однако спектр энергий может сильно зависеть от граничных условий, что характерно для неэрмитовых систем. На диаграммах показаны примеры спектров комплексных энергий в различных мнимых магнитных полях и при различных граничных условиях.

#уровни_Ландау #неэрмитовы_системы

А вот еще любопытный пример из статьи из предыдущего поста: мнимый эффект Ааронова-Бома, возникающий в мнимом магнитном поле.

Если при обычном эффекте Ааронова-Бома волновая функция частицы, обходящей замкнутый контур, приобретает фазу, пропорциональную магнитному потоку внутри контура, то здесь она увеличивает или уменьшает – в зависимости от направления обхода – свою амплитуду.

На панели (а) показан прямоугольный контур, вдоль которого волновой пакет ведется изменяемой во времени внешней силой, панели (b) и (c) показывают, что происходит с амплитудой волновой функции при обходе этого контура против и по часовой стрелке. Хотя динамика затухания или, наоборот, роста амплитуды зависят от калибровки мнимого векторного потенциала (синяя и красная кривые), финальный результат от нее не зависит.

#уровни_Ландау #неэрмитовы_системы

А вот недавний эксперимент, демонстрирующий неэрмитовы аналоги фазы Берри и эффекта Ааронова-Бома. Электронная обратная связь, подающая нужные силы на два механических осциллятора, позволяет моделировать неэрмитову систему. В частности, сила упругого воздействия первого осциллятора на второй J–δJ может отличаться от силы обратного воздействия J+ δJ, что в обычной механической системе невозможно.

В пространстве параметров J, δJ и Δ (расстройки частот двух осцилляторов) имеется конусообразная область δJ² > J² + Δ², в которой PT-симметрия гамильтониана системы спонтанно нарушена. Любопытно, что ее можно считать «соленоидом», через который проходит мнимое магнитное поле.

Как следствие, при обходе параметров вокруг конуса система подвергается мнимому эффекту Ааронова-Бома: амплитуда колебаний осцилляторов снижается либо – при другом направлении обхода – повышается. Это продемонстрировано на графиках снизу для трех круговых траекторий, обходимых по и против часовой стрелки.

#неэрмитовы_системы #механика

Как известно, предел Карно η_С для КПД η достижим только в случае бесконечно медленной работы тепловой машины. Но в этой работе показано, что работа в окрестности фазового перехода позволяет асимптотически приближать η к η_С, увеличивая объем рабочего тела и при этом сохраняя мощность работы постоянной в расчете на единицу объема. Пример этого показан на графике для случая титаната диспрозия в окрестности образования фазы спинового льда, где N – число степеней свободы рабочего тела, пропорциональное его объему.

Причина такого странного эффекта в том, что в окрестности перехода – в критическом режиме – теплоемкость рабочего тела неэкстенсивна. С ростом N она ведет себя как С ~ N^(1+α/dν), где α, ν и d – критические индексы и размерность системы. Таким образом, при α/dν > 0 она растет быстрее объема. Это объясняется тем, что из-за критических флуктуаций, охватывающих большие пространственные масштабы, рабочее тело нужно рассматривать как единую систему, а не как совокупность независимых частей.

#термодинамика

Эффект Хонга-У-Мандела – это двухфотонная интерференция, демонстрирующая бозонную статистику фотонов. Он состоит в том, что два фотона в совместном фоковском состоянии |1,1> (например, рожденные в нелинейно-оптическом кристалле), проходя через симметричный светоделитель, дают состояние (|2,0> + |0,2>)/√2. Получается, что в конце оба фотона попадают либо в верхний, либо в нижний детектор, то есть подвергаются группировке. Вероятность же одновременного срабатывания обоих детекторов должна быть, в идеале, равна нулю.

В этом эксперименте эффект Хонга-У-Мандела продемонстрирован для поверхностных плазмонов – то есть доказано, что они тоже являются бозонами. Два фотона падают на углы крестообразного металлического образца, возбуждая там поверхностные плазмоны, которые интерферируют в центре и высвечиваются с двух других углов. Как видно на графике, по мере приближения времени задержки Δt между двумя падающими фотонами к нулю вероятность одновременного срабатывания детекторов резко снижается.

#фотоника #плазмоны

В этой формуле из Википедии для гамильтониана взаимодействия двух магнитных диполей можно заметить загадочный контактный член, пропорциональный дельта-функции δ(r).

Откуда он берется? Как объясняется в этой статье Джексона, стандартная формула для диполь-дипольного взаимодействия (первое слагаемое) отталкивается от выражения для магнитного поля B(r) = [3ȓ(m•ȓ) – m]/r³, создаваемого диполем m, которое справедливо только на достаточно больших расстояниях r. Если представить магнитный диполь в виде петли или другого пространственного распределения тока в ограниченном объеме, то внутри этого объема такая формула уже неприменима.

Добавочное магнитное поле, имеющееся внутри диполя, интегрально по объему равно (8π/3)m, так что при малом размере диполя его можно эффективно сжать в точку в виде (8π/3)mδ(r). Таким образом, суммарное поле равно B(r) = [3ȓ(m•ȓ) – m]/r³ + (8π/3)mδ(r), а энергия второго диполя m´ в этом поле H ~ –(B•m´) дает финальное выражение с дельта-функционным членом.

#объяснения #электродинамика

Важная и широко цитируемая работа, в которой была рассмотрена топологическая классификация состояний кристаллов во внешнем периодическом поле (состояний Флоке-Блоха).

Эволюция волновой функции такой системы за один период ψ(t+T)=Uψ(t) описывается унитарным оператором Флоке U. Можно, в принципе, ввести эффективный гамильтониан U=exp(–iĤT/ℏ) и строить обычную топологическую классификацию, рассматривая спектр квазиэнергий гамильтониана Ĥ. Но здесь авторы показали, что во флоке-системах возможны принципиально новые фазы, обусловленные периодическим замыканием спектра квазиэнергий.

Даже если собственные состояния Ĥ образуют топологически тривиальные зоны, возможны состояния системы с киральными краевыми модами. На рисунке снизу показан пример того, как это возможно: поочередное усиление интегралов перескока в разных направлениях «протаскивает» за собой частицы по кругу. Эффект получается похожим на действие эффективного магнитного поля в топологическом изоляторе Черна.

#топологические_материалы #состояния_Флоке

Как я недавно писал, квантовая когерентность – то есть наличие недиагональных по энергиям элементов матрицы плотности – является ценным ресурсом, который можно использовать для реализации квантовых операций или извлечения работы из тепла. Она необходима даже для элементарного отсчета времени, потому что в отсутствие когерентностей любая квантовая система стационарна.

В этой работе доказывается, что невозможна полная очистка когерентности (coherence distillation). Это процесс, при котором на основе какого-то числа частично когерентных систем («зашумленных маятников» на рисунке сверху) создается полностью когерентное – то есть квантовомеханически чистое – состояние одной или нескольких систем («чистые маятники» снизу). При этом разрешено использовать внешние ресурсы, например, вспомогательные системы или работу, не обладающие собственной когерентностью.

Автор показывает, что, хотя полная очистка когерентности невозможна, частичную ее очистку производить можно.

#квантовые_вычисления #квантовая_термодинамика