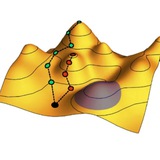
Красивые концепции устройств, основанных на тепловых метаматериалах. Чередование слоев латексной резины и силиконового эластомера делает тепловую проводимость метаматериала зависящей от координат и направления, что дает возможность управлять потоками тепла.

Тепловой щит (a) защищает свою внутреннюю область от внешнего теплового потока: как показано моделированием снизу, внутри устанавливается практически постоянная температура. Тепловой концентратор (b), наоборот, усиливает внутри себя тепловой поток на 44%. А тепловой инвертор (c) делает градиент температуры обратным по сравнению с внешним, направляя потоки тепла по спирали.

#популярное

Эта большая статья дает обзор основ теории классической и квантовой информации, а в конце выводится обобщение второго начала термодинамики для квантовых систем с обратной связью – «демонов Максвелла».

Первое неравенство, показанное на рисунке, показывает, что максимальная работа Wˢ_ext, которую можно извлечь из системы, за счет обратной связи повышается на величину, пропорциональную I_QC. Это квантово-классическая взаимная информация между системой и «демоном», показывающая, сколько бит информации о квантовом состоянии системы мы получаем в среднем в результате измерения, проводимого над ней классическим измерительным прибором.

Второе неравенство говорит о том, что этот выигрыш в извлеченной работе должен компенсироваться дополнительными затратами работы на процесс измерения (Wᴹ_meas) и последующего стирания памяти, хранящей его результат (Wᴹ_eras). Если сложить оба неравенства, окажется, что для совокупности системы и демона выполняется обычное второе начало термодинамики.

#квантовая_термодинамика

В этом эксперименте наблюдалась гибридизация в режиме сильной связи между электромагнитной модой микроволновой полости, магнонами в шарике железо-иттриевого граната и механическими колебаниями этого же шарика.

Ее можно понять так: сначала магноны связываются с электромагнитной модой в поляритоны, при этом внешняя микроволновая накачка позволяет скомпенсировать поляритонное затухание. Этот механизм, чем-то схожий с антилазированием (coherent perfect absorption), позволяет ввести систему в режим сильной связи света с веществом, который иначе подавлялся бы из-за потерь.

Далее верхний поляритон вводится в резонанс с модой деформационных колебаний шарика (она связана с магнонами благодаря магнитострикции материала). На диаграмме снизу можно видеть антипересечение при их гибридизации. Управляется оно нелинейным сдвигом энергии магнонов, который возникает из-за эффекта Керра и зависит от интенсивности накачки, отложенной по горизонтальной оси.

#поляритоны

Структура пятен, образующихся при высыхании жидкости – это вопрос, важный для изучения процессов окрашивания вообще и струйной печати в частности. Даже некоторые болезни у человека можно определять по пятнам, остающимся после высыхания капель его крови.

В этой работе исследована фрактальная структура пятен, получающихся после высыхания кофейных капель. Как показано сверху, пятна получаются кольцеобразными. Авторы сфотографировали их с увеличением, перевели в однотонный вид и составили карту линий постоянной яркости, пример которых показан на цветной диаграмме.

Фрактальная размерность γ связывает длину l петель, образуемых линями постоянной яркости, с их средним радиусом r: l ~ r^γ. Как видно из графика, γ принимает значения около 1 и 1.5, соответственно, при малых и больших r. Интерпретация этой закономерности такова: малые петли не фрактальны и ведут себя как обычные замкнутые кривые, а на больших масштабах уже проявляется статистика, характерная для случайного гауссового поля.

#популярное #фракталы

А вот интересный вопрос, затронутый в статье из предыдущего поста: почему изначально круглые капли при испарении становятся кольцевыми и оставляют после себя кольцеобразные пятна?

Этот вопрос изучался во многих работах, и ответ на него такой. Испарение капли более интенсивно идет на краях, поскольку кривизна поверхности жидкости там выше – это облегчает рассеивание пара в воздухе. Поэтому в процессе испарения образуется поток жидкости от центра к краям (это частный случай потока Марангони). Из-за этого растворенные в жидкости вещества, которые не могут испаряться, скапливаются вблизи края и образуют там твердые отложения.

Отложения формируют неоднородность поверхности, которая привязывает край капли к месту и не дает силам поверхностного натяжения сдвинуть его внутрь. Как результат, капля при последующем испарении, вместо того, чтобы просто уменьшаться в размере начиная с краев, истончается в центре и становится кольцевой.

#популярное #гидродинамика

Для моделирования распространения тепла в твердых телах используются разные методы: полностью квантовые подходы (например, уравнения Линдблада или неравновесные функции Грина) на малых масштабах, полуклассические уравнения Больцмана и методы Монте-Карло на средних масштабах и, наконец, классические уравнения теплопроводности на крупных масштабах. Здесь описывается объединяющий метод, который, как утверждают авторы, применим на всех масштабах.

Название у него устрашающее: «квантово-термодинамический метод наискорейшего подъема энтропии». Но, по существу, метод не так уж сложен. Состояние системы параметризуется набором одночастичных – электронных и фононных – факторов заполнения. Для них, из соображений максимизации производства энтропии (отсюда и название метода), выводится кинетическое уравнение. Далее из кинетического уравнения выводятся уравнения баланса числа частиц и энергии, распространяющихся от одного блока образца к другому, в которых предполагается локальное тепловое равновесие.

#твердое_тело

Огненные муравьи при затоплениях спасаются, сцепляясь в большие «ковры», плавающие по воде и сохраняющие упругость. Такой ковер представлен слоем муравьев, сцепившихся лапками, по которому сверху бегают оставшиеся муравьи, ищущие, куда бы еще прицепиться.

В этом эксперименте плавающий ковер из муравьев всесторонне исследовали на механические свойства – жесткость, вязкоупругость, способность залечивать повреждения и т.д. На рисунке показан его отклик в виде механического напряжения T на деформации растяжения ε. Как видно, при небольших деформациях ковер демонстрирует упругий отклик T ~ ε, но затем начинает разрываться. Кривые, отвечающие разным скоростям растяжения έ, показывают, что при большей скорости упругость повышается, а разрыв происходит раньше.

Авторы делают вывод, что ковер из муравьев не демонстрирует вязкоупругости, характерной для многих мягких материалов, потому что при типичных скоростях растяжения муравьи не успевают перестроиться, соединившись по-новому.

#популярное #механика

А на этом рисунке из статьи из предыдущего поста запечатлен драматический момент. Плавающий ковер сцепившихся между собой огненных муравьев растягивают, и в нем уже образовалась пара больших разрывов... Но два муравья все еще героически держатся друг за друга двумя парами лапок, образуя мостик, не дающий разрывам соединиться!

Увы, силы муравьев ограничены, так что в конце концов их лапки расцепляются... Два разрыва объединяются в один большой, и это дает резкий толчок дальнейшему растяжению всего ковра.

#популярное #цитаты

Проблема знака при моделировании квантовых систем методами Монте-Карло возникает из-за того, что различные траектории, по которым производится суммирование для расчета наблюдаемых, могут давать противоположные вклады в результат. В итоге это приводит к большим ошибкам округления и накоплению ошибок, экспоненциально растущих с уменьшением температуры и ростом числа частиц.

В этой работе на примере нескольких моделей продемонстрировано, что обострение проблемы знака может служить признаком близости квантового фазового перехода. На рисунке показаны два примера с моделями Хаббарда на решетке «пчелиные соты». В первом случае (сверху) электроны отталкиваются на узле, а во втором случае (снизу) электроны бесспиновые и отталкиваются на соседних узлах. В обоих случаях видно, что средний знак <S> вкладов траекторий снижается (что свидетельствует о большом числе слагаемых противоположных знаков) вблизи точек квантовых фазовых переходов, отмеченных звездочками.

#квантовая_механика #Монте_Карло

А вот тоже интересная модель из статьи из предыдущего поста. Электроны перескакивают по квадратной решетке, отталкиваются на узле с силой U и, вдобавок, подвержены действию внешнего потенциала, имеющего противоположные значения ±Δ на двух подрешетках (это имитирует ионный кристалл).

У этой модели любопытная фазовая диаграмма. При Δ >> U и половинном заполнении образуется изолятор с волной зарядовой плотности (это нижняя часть диаграмм на рисунке), потому что электроны парами заполняют более выгодную по энергии подрешетку с потенциалом –Δ. Повышение U делает такое состояние невыгодным из-за двойных заполнений и при Δ << U (левые части диаграмм) образуется однородный изолятор Мотта-Хаббарда.

В промежутке между двумя изоляторами образуется фаза скоррелированного металла, которая обнаруживается по снижению среднего знака <S>. А два различных по природе изолятора можно отличить по противоположной чувствительности двойных заполнений к возрастанию U (нижняя диаграмма).

#квантовая_механика #сильные_корреляции

Кстати, на этом рисунке из предыдущего поста можно заметить, что производная двойных заполнений по U, посчитанная методом Монте-Карло (нижняя диаграмма), в фазе скоррелированного металла ведет себя странно.

Она сильно флуктуирует, от пикселя к пикселю, между положительными и отрицательными значениями. Это и есть проявление проблемы знака: при низких температурах и большом числе частиц накапливаются экспоненциально растущие ошибки, не дающие нормально моделировать систему. Вне фазы скоррелированного металла все считается нормально.

#Монте_Карло

И вот, пожалуй, самая интересная модель из статьи, посвященной проблеме знака. Это электроны на квадратной решетке, отталкивающиеся на узле – простейшая модель, описывающая высокотемпературные сверхпроводники на основе оксида меди.

На рисунке показаны фазовые диаграммы на осях уровня электронного допирования ρ и температуры T. Как видно, средний знак <S> резко снижается внутри – предположительно! – сверхпроводящего купола. Однако подтвердить, что это действительно сверхпроводящая фаза, мешает та же проблема знака.

Восприимчивость к d-волновому параметру порядка, расходимость которой должна указывать на сверхпроводимость, сильно флуктуирует внутри купола из-за погрешностей расчета (диаграмма справа сверху). Тем не менее, даже снаружи купола, вместе с однородной спиновой восприимчивостью χ, они приближенно очерчивают область псевдощели, имеющуюся вблизи половинного заполнения ρ = 1.

#сверхпроводимость #сильные_корреляции

Сейчас бурно развивается физика активной материи, состоящей из частиц, которые могут самостоятельно двигаться, используя либо собственные источники энергии (как бактерии или стайные животные), либо внешний ресурс (например, несимметричные частицы, движущиеся благодаря градиенту температур под внешним освещением). Неудивительно, что важнейший вопрос здесь – баланс и диссипация энергии, используемой частицами для движения.

Один из видов такой материи – это активные кристаллы, образовавшиеся в результате конденсации активных частиц в плотную решетку. В этой работе изучалось производство энтропии в активном кристалле, сопровождающей превращение энергии, идущей на движение частиц, в тепло окружающей среды. Оказалось, что в спектре производства энтропии σ(ω,q), показанном на графиках, появляется новая коллективная мода, ответственная за диссипацию – энтропон. Она четко выделяется в сильно неравновесном режиме, а при стремлении к равновесию сливается с обычными фононами кристалла.

#стохастическая_термодинамика

SWAP-двигатель – это одна из простейших квантовых тепловых машин, состоящая всего из двух кубитов и работающая по циклу Отто.

Первый кубит A изначально находится в равновесии с нагревателем, второй кубит B находится в равновесии с холодильником. Энергии возбуждений кубитов при этом ε_A и ε_B, а обратные температуры нагревателя и холодильника – β_A < β_B. Над кубитами проводится двухкубитная операция SWAP, переставляющая их состояния (но не энергии возбуждений). Если ε_A > ε_B, то при совершении этой операции из системы извлекается работа, поскольку кубит A после нагревателя возбужден сильнее. Дальше следует подождать, пока кубиты снова термализуются, и можно все повторять.

На диаграмме справа показана средняя работа <W> затрачиваемая на операцию SWAP, как функция параметров системы. В синей области <W> < 0, то есть мы извлекаем работу из системы. На графиках снизу дается разбивка баланса энергии на количества тепла Q_A и Q_B, получаемые от нагревателя и холодильника, и работу W.

#квантовая_термодинамика

В этой работе продемонстрирована термодинамическая роль квантовых корреляций, которые могут использоваться для повышения КПД тепловых машин и даже превышения классического предела Карно.

Здесь рассматривается SWAP-двигатель, принцип действия которого я описал в предыдущем посте. Только в него вносится модификация: после термализации кубитов между ними создается корреляция, то есть кубиты квантово запутываются.

На цветных диаграммах показано, что при наличии корреляций (справа) расширяется область параметров, при которых система работает как тепловой двигатель (затрачиваемая работа <W> отрицательна), при этом извлекаемая работа –<W> демонстрирует неслабый рост. А на графиках снизу видно, что при наличии корреляций КПД η может превышать предел Карно. Хотя не стоит забывать, что создание корреляций тоже имеет свою цену, так что обобщенное второе начало термодинамики здесь выполняется.

Авторы не просто провели расчеты, но и реализовали все это на квантовом компьютере ibmq_manila.

#квантовая_термодинамика

Кстати говоря, режим работы тепловой машины, при котором рабочее тело получает положительное количество тепла <Q_A> от нагревателя, отрицательное количество тепла <Q_B> от холодильника (то есть отдает ему теплоту), и на это затрачивается положительная работа <W>, называют тепловым ускорителем (thermal accelerator).

Хотя, по существу, это кулер: вместо того, чтобы извлекать работу из перетекания тепла от нагревателя к холодильнику (как происходит в тепловом двигателе, thermal engine), мы, наоборот, затрачиваем работу на то, чтобы оно происходило еще быстрее.

В этом эксперименте реализован аналог преломления светового импульса, происходящий не в пространстве, а во времени.

Как показано на схеме слева, при резком изменении показателя преломления n в пространстве волна меняет свой волновой вектор (преломляется), сохраняя частоту. Если же показатель преломления резко и однородно меняется как функция времени (схема справа), у распространяющейся волны меняется частота, но сохраняется волновой вектор.

Такое резкое изменение реализовано накачкой оксида индия-олова: Re[ε] у него проходит через ноль вблизи 1200 нм, и вблизи этой длины волны можно достичь значительного относительного изменения n(t). На диаграмме справа показано, как, при различных временах задержки τ между импульсом накачки и запущенным в среду зондирующим импульсом, меняется спектр последнего. При τ < 0 n(t) увеличивается уже во время его распространения, так что «преломление во времени» дает красное смещение, а при τ > 0 n(t) уменьшается, так что мы видим синее смещение.

#фотоника

Для определения степени запутанности двух квантовых систем нужно, по-хорошему, полностью измерить их совместную матрицу плотности, а потом еще и провести расчеты, экспоненциально усложняющиеся с ростом размера системы. Поэтому задачу упрощают, используя индикаторы запутанности (entanglement witnesses) – величины, которые относительно легко измеряются и при этом дают для степени запутанности оценку снизу.

В этом эксперименте был использован новый индикатор запутанности, основанный на совместной статистике нескольких переменных X_a, X_b, K_a, K_b. Это могут быть, как в данном случае, распределение координат и волновых векторов по осям (x, y) двух запутанных фотонов. Адаптивный алгоритм сам определяет, в каком месте с каким разрешением их измерять.

В результате удалось довольно быстро измерить запутанность в пространстве размерности 512⁴ (более 68 миллиардов) – это в 10¹⁸ быстрее, чем напрямую, при помощи томографии матрицы плотности.

#квантовая_механика #квантовые_вычисления

Кстати говоря, степень квантовой запутанности двух фотонов, измеренная в работе из предыдущего поста, составляет 7.11 бита, как показано оранжевой кривой. Точнее, она измеряется в ебитах (ebits, entanglement bits).

Не знаю как сейчас, но на момент публикации в 2019 году это была самая большая по величине запутанность, когда-либо измеренная между любыми двумя квантовыми системами.

#квантовая_механика #квантовые_вычисления

Очередная работа из серии «мы реализовали в эксперименте простейшую квантовую систему с 2-3 энергетическими уровнями и убедились, что квантовая механика таки работает».

В этот раз при помощи атомов в оптических ловушках реализовали хаббардовский димер – две отталкивающиеся частицы со спином 1/2 в двух соседних потенциальных ямах. Это элементарный строительный блок модели Хаббарда, используемой для описания сильно-коррелированных систем и, в частности, высокотемпературных сверхпроводников.

На графике сверху показано как должны себя вести 4 энергетических уровня димера при изменении взаимодействия атомов на узле U. При U→+∞ состояния |LL> и |RR> с двойными заполнениями левой либо правой ямы выталкиваются вверх. Как видно на графиках снизу, в основном состоянии при этом обе частицы предпочитают распределяться по разным ямам, а в высоко возбужденном – находятся в одной яме. Измеренные вероятности (точки) согласуются с предсказаниями квантовой механики (линиями).

#квантовая_механика #сильные_корреляции

Встречайте Imagen – новую нейросеть, генерирующую фотореалистичные изображения по словесным описаниям. В статье можно найти красивые примеры ее работы.

На рисунке описана ее архитектура. Текстовое описание поступает в языковую модель – нейросеть архитектуры T5-XXL (это трансформер, как и знаменитый ChatGPT), которая обучается на корпусе текстов и умеет выделять сжатые представления фраз (embeddings). Они подаются на три последовательных каскада диффузионных моделей: используя метод обратной диффузии, эти модели превращают случайный шум в осмысленное изображение.

Принцип работы такого метода я описывал в отдельной статье. При этом диффузия определенным образом «направляется» как сжатым представлением текстовой фразы, так и более грубыми изображениями с предыдущего каскада.

Авторы используют ряд тестов (в том числе с использованием оценок людей), демонстрирующих, что Imagen по всем параметрам превосходит нейросети-конкуренты: DALL-E 2, GLIDE, VQ-GAN+CLIP и Latent Diffusion.

#нейронные_сети #популярное