Любопытные формулы для сверхтекучей плотности, которую авторы этой статьи называют «друдевским весом» D_w.
Как показано сверху, она выражается через среднюю кинетическую энергию и сумму, содержащую матричные элементы оператора тока J между основным |Ψ_0> и точными многочастичными возбужденными состояниями |Ψ_m>. Эта сумма похожа – с точностью до другой степени знаменателя – на выражение для многочастичной квантовой метрики g(0) на оси проходящего через систему магнитного потока. Если все энергии возбуждений E_m – E_0 не меньше щели ε, мы получаем неравенство, показанное снизу.
Первое слагаемое обычно отрицательно, так что g уменьшает сверхтекучую плотность по сравнению с ее максимально возможным значением. Интерпретация этого факта такова: чем выше многочастичная квантовая метрика g, тем сильнее многочастичная волновая функция системы искажается при внесении возмущения, создающего сверхтекучий ток. Это не дает системе просто ускоряться как целое, уменьшая сверхтекучий отклик.
#сверхтекучесть
Как показано сверху, она выражается через среднюю кинетическую энергию и сумму, содержащую матричные элементы оператора тока J между основным |Ψ_0> и точными многочастичными возбужденными состояниями |Ψ_m>. Эта сумма похожа – с точностью до другой степени знаменателя – на выражение для многочастичной квантовой метрики g(0) на оси проходящего через систему магнитного потока. Если все энергии возбуждений E_m – E_0 не меньше щели ε, мы получаем неравенство, показанное снизу.
Первое слагаемое обычно отрицательно, так что g уменьшает сверхтекучую плотность по сравнению с ее максимально возможным значением. Интерпретация этого факта такова: чем выше многочастичная квантовая метрика g, тем сильнее многочастичная волновая функция системы искажается при внесении возмущения, создающего сверхтекучий ток. Это не дает системе просто ускоряться как целое, уменьшая сверхтекучий отклик.
#сверхтекучесть
Недавно я писал о том, как добавление солей нарушает скоррелированность дипольных моментов молекул воды и, тем самым, понижает ее диэлектрическую проницаемость ε. А в этой работе показано, почему у чистой воды высокая ε: действительно, она обусловлена тем, что из-за направленности водородных связей дипольные моменты соседних молекул воды направлены почти в одну сторону.
Простейшая теория линейного отклика дает формулу ε = 1 + (4π/3)<M²>/VT, где M – суммарный электрический дипольный момент всех молекул в объеме V. При этом <M²> = Nμ²G, где μ –дипольный момент каждой молекулы, G – мера их скоррелированности по направлениям, которую можно посчитать как интеграл от парной корреляционной функции c_m(r) ~ <μ(0)•μ(r)>. На графике видно, что c_m(r) имеет пик на расстоянии между ближайшими соседями – там же, где похожий пик демонстрирует корреляционная функция для атомов кислорода g_OO.
Из-за значительной сонаправленности соседних диполей G достигает 2.2 – это и есть вклад корреляций в увеличение ε.
#химия
Простейшая теория линейного отклика дает формулу ε = 1 + (4π/3)<M²>/VT, где M – суммарный электрический дипольный момент всех молекул в объеме V. При этом <M²> = Nμ²G, где μ –дипольный момент каждой молекулы, G – мера их скоррелированности по направлениям, которую можно посчитать как интеграл от парной корреляционной функции c_m(r) ~ <μ(0)•μ(r)>. На графике видно, что c_m(r) имеет пик на расстоянии между ближайшими соседями – там же, где похожий пик демонстрирует корреляционная функция для атомов кислорода g_OO.
Из-за значительной сонаправленности соседних диполей G достигает 2.2 – это и есть вклад корреляций в увеличение ε.
#химия
Квантовый выход фотолюминесценции – это число фотонов, испускаемых в расчете на одну электрон-дырочную пару, образующуюся при накачке. У двумерного полупроводника MoS₂ он обычно составляет 1%. А здесь, после обработки образцов суперкислотой, его удалось повысить практически до 100%!
Сверху видно, как отличается люминесценция в только что изготовленном (синяя кривая) и в обработанном (красная кривая) образцах – по интенсивности она увеличивается в 190 раз, хотя форма спектральной линии сохраняется. Внизу показано, как квантовый выход и время жизни носителей (измеренное по сверхбыстрой люминесценции) зависят от интенсивности накачки. После обработки обе величины увеличиваются на два порядка. Но при сильной накачке они постепенно снижаются из-за образования и рекомбинации биэкситонов при высокой концентрации электрон-дырочных пар.
Авторы предполагают, что обработка суперкислотой подавляет процессы нерадиативной рекомбинации, удаляя с образца примеси и пассивируя дефекты.
#дихалькогениды_переходных_металлов
Сверху видно, как отличается люминесценция в только что изготовленном (синяя кривая) и в обработанном (красная кривая) образцах – по интенсивности она увеличивается в 190 раз, хотя форма спектральной линии сохраняется. Внизу показано, как квантовый выход и время жизни носителей (измеренное по сверхбыстрой люминесценции) зависят от интенсивности накачки. После обработки обе величины увеличиваются на два порядка. Но при сильной накачке они постепенно снижаются из-за образования и рекомбинации биэкситонов при высокой концентрации электрон-дырочных пар.
Авторы предполагают, что обработка суперкислотой подавляет процессы нерадиативной рекомбинации, удаляя с образца примеси и пассивируя дефекты.
#дихалькогениды_переходных_металлов
👍3
Сверхизлучение Дике состоит в том, что при взаимодействии массива N двухуровневых систем с одной электромагнитной модой скорость излучения ведет себя как N². Это кооперативный эффект, обусловленный конструктивной интерференцией процессов излучения каждого диполя. А в этом эксперименте наблюдался обратный процесс сверхпоглощения.
Молекулы органического полупроводника, помещенные в полимерную матрицу и в оптическую микрополость, поглощают импульс накачки, из-за чего их способность к дальнейшему поглощению подавляется. По скорости увеличения прозрачности после накачки, показанной на графике сверху, можно судить о скорости процесса поглощения.
Как показано снизу, мощность поглощаемого излучения в расчете на одну молекулу P_max растет с числом молекул N, что свидетельствует о кооперативности. Процессы сверхизлучения и сверхпоглощения открывают путь к созданию квантовых батарей, использующих когерентность для сверхэкстенсивного увеличения объема хранимой энергии или скорости своей зарядки и разрядки.
#фотоника
Молекулы органического полупроводника, помещенные в полимерную матрицу и в оптическую микрополость, поглощают импульс накачки, из-за чего их способность к дальнейшему поглощению подавляется. По скорости увеличения прозрачности после накачки, показанной на графике сверху, можно судить о скорости процесса поглощения.
Как показано снизу, мощность поглощаемого излучения в расчете на одну молекулу P_max растет с числом молекул N, что свидетельствует о кооперативности. Процессы сверхизлучения и сверхпоглощения открывают путь к созданию квантовых батарей, использующих когерентность для сверхэкстенсивного увеличения объема хранимой энергии или скорости своей зарядки и разрядки.
#фотоника
❤5
Недавно я писал о достижении термоядерного синтеза лазерным облучением кластеров дейтерия, а здесь он достигнут весьма оригинальным образом – при помощи нагрева пироэлектрического кристалла, создающего сильное электрическое поле.
Как показано на рисунке, кристалл пироэлектрика прикреплен к нагревателю, а с другой стороны на него наложен медный диск с вольфрамовой иглой. При нагреве кристалла на его краях образуется напряжение 80 кВ, а вблизи острия иглы электрическое поле усиливается до 25 В/нм. Это поле ионизует и разгоняет дейтерий, заполняющий герметичную камеру с кристаллом, и разогнанные до 115 кэВ ядра сталкиваются с другими ядрами дейтерия в мишени, содержащей ErD₂. В результате слияния ядер дейтерия образуются ядра ³He и нейтроны с энергией 2.45 МэВ.
На графиках справа показано, как, в течение одного запуска эксперимента, постепенно нарастает температура кристалла, регистрируются рентгеновские лучи от вторичных электронов, ионный ток через сетку и нейтроны от ядерного синтеза.
#ядерная_физика
Как показано на рисунке, кристалл пироэлектрика прикреплен к нагревателю, а с другой стороны на него наложен медный диск с вольфрамовой иглой. При нагреве кристалла на его краях образуется напряжение 80 кВ, а вблизи острия иглы электрическое поле усиливается до 25 В/нм. Это поле ионизует и разгоняет дейтерий, заполняющий герметичную камеру с кристаллом, и разогнанные до 115 кэВ ядра сталкиваются с другими ядрами дейтерия в мишени, содержащей ErD₂. В результате слияния ядер дейтерия образуются ядра ³He и нейтроны с энергией 2.45 МэВ.
На графиках справа показано, как, в течение одного запуска эксперимента, постепенно нарастает температура кристалла, регистрируются рентгеновские лучи от вторичных электронов, ионный ток через сетку и нейтроны от ядерного синтеза.
#ядерная_физика
👍1
Красивый расчет момента инерции сверхтекучего бозе-конденсата в гармонической ловушке. Если ловушка анизотропная, то есть имеет эллиптическую форму, ее можно вращать, частично увлекая и атомный газ. Расчет момента инерции Θ как функции отклика углового момента на вращение ловушки дает два вклада.
Первый вклад, пропорциональный числу атомов в конденсате N₀, обусловлен анизотропным вращением конденсатного облака вслед за ловушкой. Это вращение, как ни странно, безротационное – ротор поля скоростей для него равен нулю, как и должно быть для конденсата. Второй вклад – это момент инерции жесткого эллипсоида Θ_rig, умноженный на число тепловых возбуждений N – N₀. Они, в отличие от конденсата, увлекаются вращением ловушки полностью.
Из-за неполного увлечения конденсата получается снижение момента инерции по сравнению с твердотельным вращением: Θ < Θ_rig. На графике справа показано как, по мере роста температуры, снижается доля конденсата, а момент инерции Θ постепенно возрастает до Θ_rig.
#сверхтекучесть
Первый вклад, пропорциональный числу атомов в конденсате N₀, обусловлен анизотропным вращением конденсатного облака вслед за ловушкой. Это вращение, как ни странно, безротационное – ротор поля скоростей для него равен нулю, как и должно быть для конденсата. Второй вклад – это момент инерции жесткого эллипсоида Θ_rig, умноженный на число тепловых возбуждений N – N₀. Они, в отличие от конденсата, увлекаются вращением ловушки полностью.
Из-за неполного увлечения конденсата получается снижение момента инерции по сравнению с твердотельным вращением: Θ < Θ_rig. На графике справа показано как, по мере роста температуры, снижается доля конденсата, а момент инерции Θ постепенно возрастает до Θ_rig.
#сверхтекучесть
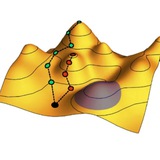
В этой работе показано, как наложением на кристалл осциллирующего электрического поля можно создать систему с отрицательной температурой.
Можно показать, что поле амплитудой K, осциллирующее с частотой Ω, приводит к эффективной перенормировке интеграла перескока: J → J₀(K/ Ω)×J, где J₀ – функция Бесселя нулевого порядка. Поскольку при некоторых значениях аргумента она отрицательна, интеграл перескока J можно сделать отрицательным, что приводит к перевороту дисперсии E(k) = –2J cos(ka).
Если осциллирующее поле включается достаточно резко, но аккуратно, то заполнения одночастичных состояний фермионов N(ω,t) переворачиваются вместе с дисперсией. Как показано на графике слева, это приводит к инверсии населенностей и отрицательной температуре. График справа показывает, как, после включения поля, суммарная энергия частиц (синяя кривая) осциллирует, но в среднем положительна (черная кривая). Хотя до включения поля, в основном состоянии системы, она была отрицательной.
#квантовая_термодинамика
Можно показать, что поле амплитудой K, осциллирующее с частотой Ω, приводит к эффективной перенормировке интеграла перескока: J → J₀(K/ Ω)×J, где J₀ – функция Бесселя нулевого порядка. Поскольку при некоторых значениях аргумента она отрицательна, интеграл перескока J можно сделать отрицательным, что приводит к перевороту дисперсии E(k) = –2J cos(ka).
Если осциллирующее поле включается достаточно резко, но аккуратно, то заполнения одночастичных состояний фермионов N(ω,t) переворачиваются вместе с дисперсией. Как показано на графике слева, это приводит к инверсии населенностей и отрицательной температуре. График справа показывает, как, после включения поля, суммарная энергия частиц (синяя кривая) осциллирует, но в среднем положительна (черная кривая). Хотя до включения поля, в основном состоянии системы, она была отрицательной.
#квантовая_термодинамика
Обзор по электромагнитно-индуцированной прозрачности (electromagnetically induced transparency, EIT) – когерентному оптическому явлению, при котором в веществе, энергетические уровни которого «одеваются» дополнительным электромагнитным полем, между двумя пиками поглощения возникает узкая полоса прозрачности.
Это видно на графике для мнимой части функции отклика Im[χ], при этом Re[χ] в области прозрачности демонстрирует сильнейшую нормальную дисперсию, а также резко усиливается нелинейный отклик | χ⁽³⁾|. Можно сказать, что процессы поглощения в двух пиках интерферируют деструктивно, а нелинейные процессы интерферируют конструктивно.
EIT произвела настоящую революцию в оптике и связана с такими явлениями, как безынверсионная лазерная генерация, стимулированный рамановский адиабатический переход (STIRAP) и множество сверхсильных нелинейных эффектов. В эту же копилку идут нашумевшие эксперименты, где свет в веществе распространялся со сверхмалой скоростью или вовсе останавливался на небольшое время.
#фотоника
Это видно на графике для мнимой части функции отклика Im[χ], при этом Re[χ] в области прозрачности демонстрирует сильнейшую нормальную дисперсию, а также резко усиливается нелинейный отклик | χ⁽³⁾|. Можно сказать, что процессы поглощения в двух пиках интерферируют деструктивно, а нелинейные процессы интерферируют конструктивно.
EIT произвела настоящую революцию в оптике и связана с такими явлениями, как безынверсионная лазерная генерация, стимулированный рамановский адиабатический переход (STIRAP) и множество сверхсильных нелинейных эффектов. В эту же копилку идут нашумевшие эксперименты, где свет в веществе распространялся со сверхмалой скоростью или вовсе останавливался на небольшое время.
#фотоника
❤3
Электромагнитно-индуцированная прозрачность, о которой я писал в предыдущем посте, в простейшем случае возникает в Λ-схеме с тремя энергетическими уровнями, связанными двумя электромагнитными переходами.
Поле накачки связывает между собой два возбужденных состояния |2> и |3>, из-за чего образуется дублет Аутлера-Таунса – два «одетых» излучением и расщепленных между собой квазиэнергетических уровня. Если в отсутствие накачки лишь состояние |3> связано дипольным переходом с основным состоянием |1> (является оптически светлым), то теперь оба состояния дублета – частично светлые в меру весовой доли |3> в их волновых функциях.
Если поле накачки достаточно сильное, то в спектре поглощения виден хорошо расщепленный дублет Аутлера-Таунса (см. график слева). При меньшей амплитуде накачки компоненты дублета сдвигаются, но между ними остается область нулевого поглощения, обусловленная их деструктивной интерференцией (график справа). Общая площадь под графиком при этом сохраняется.
#фотоника
Поле накачки связывает между собой два возбужденных состояния |2> и |3>, из-за чего образуется дублет Аутлера-Таунса – два «одетых» излучением и расщепленных между собой квазиэнергетических уровня. Если в отсутствие накачки лишь состояние |3> связано дипольным переходом с основным состоянием |1> (является оптически светлым), то теперь оба состояния дублета – частично светлые в меру весовой доли |3> в их волновых функциях.
Если поле накачки достаточно сильное, то в спектре поглощения виден хорошо расщепленный дублет Аутлера-Таунса (см. график слева). При меньшей амплитуде накачки компоненты дублета сдвигаются, но между ними остается область нулевого поглощения, обусловленная их деструктивной интерференцией (график справа). Общая площадь под графиком при этом сохраняется.
#фотоника
👍3
Красивые концепции устройств, основанных на тепловых метаматериалах. Чередование слоев латексной резины и силиконового эластомера делает тепловую проводимость метаматериала зависящей от координат и направления, что дает возможность управлять потоками тепла.
Тепловой щит (a) защищает свою внутреннюю область от внешнего теплового потока: как показано моделированием снизу, внутри устанавливается практически постоянная температура. Тепловой концентратор (b), наоборот, усиливает внутри себя тепловой поток на 44%. А тепловой инвертор (c) делает градиент температуры обратным по сравнению с внешним, направляя потоки тепла по спирали.
#популярное
Тепловой щит (a) защищает свою внутреннюю область от внешнего теплового потока: как показано моделированием снизу, внутри устанавливается практически постоянная температура. Тепловой концентратор (b), наоборот, усиливает внутри себя тепловой поток на 44%. А тепловой инвертор (c) делает градиент температуры обратным по сравнению с внешним, направляя потоки тепла по спирали.
#популярное
👍2
Эта большая статья дает обзор основ теории классической и квантовой информации, а в конце выводится обобщение второго начала термодинамики для квантовых систем с обратной связью – «демонов Максвелла».
Первое неравенство, показанное на рисунке, показывает, что максимальная работа Wˢ_ext, которую можно извлечь из системы, за счет обратной связи повышается на величину, пропорциональную I_QC. Это квантово-классическая взаимная информация между системой и «демоном», показывающая, сколько бит информации о квантовом состоянии системы мы получаем в среднем в результате измерения, проводимого над ней классическим измерительным прибором.
Второе неравенство говорит о том, что этот выигрыш в извлеченной работе должен компенсироваться дополнительными затратами работы на процесс измерения (Wᴹ_meas) и последующего стирания памяти, хранящей его результат (Wᴹ_eras). Если сложить оба неравенства, окажется, что для совокупности системы и демона выполняется обычное второе начало термодинамики.
#квантовая_термодинамика
Первое неравенство, показанное на рисунке, показывает, что максимальная работа Wˢ_ext, которую можно извлечь из системы, за счет обратной связи повышается на величину, пропорциональную I_QC. Это квантово-классическая взаимная информация между системой и «демоном», показывающая, сколько бит информации о квантовом состоянии системы мы получаем в среднем в результате измерения, проводимого над ней классическим измерительным прибором.
Второе неравенство говорит о том, что этот выигрыш в извлеченной работе должен компенсироваться дополнительными затратами работы на процесс измерения (Wᴹ_meas) и последующего стирания памяти, хранящей его результат (Wᴹ_eras). Если сложить оба неравенства, окажется, что для совокупности системы и демона выполняется обычное второе начало термодинамики.
#квантовая_термодинамика
В этом эксперименте наблюдалась гибридизация в режиме сильной связи между электромагнитной модой микроволновой полости, магнонами в шарике железо-иттриевого граната и механическими колебаниями этого же шарика.
Ее можно понять так: сначала магноны связываются с электромагнитной модой в поляритоны, при этом внешняя микроволновая накачка позволяет скомпенсировать поляритонное затухание. Этот механизм, чем-то схожий с антилазированием (coherent perfect absorption), позволяет ввести систему в режим сильной связи света с веществом, который иначе подавлялся бы из-за потерь.
Далее верхний поляритон вводится в резонанс с модой деформационных колебаний шарика (она связана с магнонами благодаря магнитострикции материала). На диаграмме снизу можно видеть антипересечение при их гибридизации. Управляется оно нелинейным сдвигом энергии магнонов, который возникает из-за эффекта Керра и зависит от интенсивности накачки, отложенной по горизонтальной оси.
#поляритоны
Ее можно понять так: сначала магноны связываются с электромагнитной модой в поляритоны, при этом внешняя микроволновая накачка позволяет скомпенсировать поляритонное затухание. Этот механизм, чем-то схожий с антилазированием (coherent perfect absorption), позволяет ввести систему в режим сильной связи света с веществом, который иначе подавлялся бы из-за потерь.
Далее верхний поляритон вводится в резонанс с модой деформационных колебаний шарика (она связана с магнонами благодаря магнитострикции материала). На диаграмме снизу можно видеть антипересечение при их гибридизации. Управляется оно нелинейным сдвигом энергии магнонов, который возникает из-за эффекта Керра и зависит от интенсивности накачки, отложенной по горизонтальной оси.
#поляритоны
Структура пятен, образующихся при высыхании жидкости – это вопрос, важный для изучения процессов окрашивания вообще и струйной печати в частности. Даже некоторые болезни у человека можно определять по пятнам, остающимся после высыхания капель его крови.
В этой работе исследована фрактальная структура пятен, получающихся после высыхания кофейных капель. Как показано сверху, пятна получаются кольцеобразными. Авторы сфотографировали их с увеличением, перевели в однотонный вид и составили карту линий постоянной яркости, пример которых показан на цветной диаграмме.
Фрактальная размерность γ связывает длину l петель, образуемых линями постоянной яркости, с их средним радиусом r: l ~ r^γ. Как видно из графика, γ принимает значения около 1 и 1.5, соответственно, при малых и больших r. Интерпретация этой закономерности такова: малые петли не фрактальны и ведут себя как обычные замкнутые кривые, а на больших масштабах уже проявляется статистика, характерная для случайного гауссового поля.
#популярное #фракталы
В этой работе исследована фрактальная структура пятен, получающихся после высыхания кофейных капель. Как показано сверху, пятна получаются кольцеобразными. Авторы сфотографировали их с увеличением, перевели в однотонный вид и составили карту линий постоянной яркости, пример которых показан на цветной диаграмме.
Фрактальная размерность γ связывает длину l петель, образуемых линями постоянной яркости, с их средним радиусом r: l ~ r^γ. Как видно из графика, γ принимает значения около 1 и 1.5, соответственно, при малых и больших r. Интерпретация этой закономерности такова: малые петли не фрактальны и ведут себя как обычные замкнутые кривые, а на больших масштабах уже проявляется статистика, характерная для случайного гауссового поля.
#популярное #фракталы
❤1
А вот интересный вопрос, затронутый в статье из предыдущего поста: почему изначально круглые капли при испарении становятся кольцевыми и оставляют после себя кольцеобразные пятна?
Этот вопрос изучался во многих работах, и ответ на него такой. Испарение капли более интенсивно идет на краях, поскольку кривизна поверхности жидкости там выше – это облегчает рассеивание пара в воздухе. Поэтому в процессе испарения образуется поток жидкости от центра к краям (это частный случай потока Марангони). Из-за этого растворенные в жидкости вещества, которые не могут испаряться, скапливаются вблизи края и образуют там твердые отложения.
Отложения формируют неоднородность поверхности, которая привязывает край капли к месту и не дает силам поверхностного натяжения сдвинуть его внутрь. Как результат, капля при последующем испарении, вместо того, чтобы просто уменьшаться в размере начиная с краев, истончается в центре и становится кольцевой.
#популярное #гидродинамика
Этот вопрос изучался во многих работах, и ответ на него такой. Испарение капли более интенсивно идет на краях, поскольку кривизна поверхности жидкости там выше – это облегчает рассеивание пара в воздухе. Поэтому в процессе испарения образуется поток жидкости от центра к краям (это частный случай потока Марангони). Из-за этого растворенные в жидкости вещества, которые не могут испаряться, скапливаются вблизи края и образуют там твердые отложения.
Отложения формируют неоднородность поверхности, которая привязывает край капли к месту и не дает силам поверхностного натяжения сдвинуть его внутрь. Как результат, капля при последующем испарении, вместо того, чтобы просто уменьшаться в размере начиная с краев, истончается в центре и становится кольцевой.
#популярное #гидродинамика
👍2
Для моделирования распространения тепла в твердых телах используются разные методы: полностью квантовые подходы (например, уравнения Линдблада или неравновесные функции Грина) на малых масштабах, полуклассические уравнения Больцмана и методы Монте-Карло на средних масштабах и, наконец, классические уравнения теплопроводности на крупных масштабах. Здесь описывается объединяющий метод, который, как утверждают авторы, применим на всех масштабах.
Название у него устрашающее: «квантово-термодинамический метод наискорейшего подъема энтропии». Но, по существу, метод не так уж сложен. Состояние системы параметризуется набором одночастичных – электронных и фононных – факторов заполнения. Для них, из соображений максимизации производства энтропии (отсюда и название метода), выводится кинетическое уравнение. Далее из кинетического уравнения выводятся уравнения баланса числа частиц и энергии, распространяющихся от одного блока образца к другому, в которых предполагается локальное тепловое равновесие.
#твердое_тело
Название у него устрашающее: «квантово-термодинамический метод наискорейшего подъема энтропии». Но, по существу, метод не так уж сложен. Состояние системы параметризуется набором одночастичных – электронных и фононных – факторов заполнения. Для них, из соображений максимизации производства энтропии (отсюда и название метода), выводится кинетическое уравнение. Далее из кинетического уравнения выводятся уравнения баланса числа частиц и энергии, распространяющихся от одного блока образца к другому, в которых предполагается локальное тепловое равновесие.
#твердое_тело
Огненные муравьи при затоплениях спасаются, сцепляясь в большие «ковры», плавающие по воде и сохраняющие упругость. Такой ковер представлен слоем муравьев, сцепившихся лапками, по которому сверху бегают оставшиеся муравьи, ищущие, куда бы еще прицепиться.
В этом эксперименте плавающий ковер из муравьев всесторонне исследовали на механические свойства – жесткость, вязкоупругость, способность залечивать повреждения и т.д. На рисунке показан его отклик в виде механического напряжения T на деформации растяжения ε. Как видно, при небольших деформациях ковер демонстрирует упругий отклик T ~ ε, но затем начинает разрываться. Кривые, отвечающие разным скоростям растяжения έ, показывают, что при большей скорости упругость повышается, а разрыв происходит раньше.
Авторы делают вывод, что ковер из муравьев не демонстрирует вязкоупругости, характерной для многих мягких материалов, потому что при типичных скоростях растяжения муравьи не успевают перестроиться, соединившись по-новому.
#популярное #механика
В этом эксперименте плавающий ковер из муравьев всесторонне исследовали на механические свойства – жесткость, вязкоупругость, способность залечивать повреждения и т.д. На рисунке показан его отклик в виде механического напряжения T на деформации растяжения ε. Как видно, при небольших деформациях ковер демонстрирует упругий отклик T ~ ε, но затем начинает разрываться. Кривые, отвечающие разным скоростям растяжения έ, показывают, что при большей скорости упругость повышается, а разрыв происходит раньше.
Авторы делают вывод, что ковер из муравьев не демонстрирует вязкоупругости, характерной для многих мягких материалов, потому что при типичных скоростях растяжения муравьи не успевают перестроиться, соединившись по-новому.
#популярное #механика
😁3
А на этом рисунке из статьи из предыдущего поста запечатлен драматический момент. Плавающий ковер сцепившихся между собой огненных муравьев растягивают, и в нем уже образовалась пара больших разрывов... Но два муравья все еще героически держатся друг за друга двумя парами лапок, образуя мостик, не дающий разрывам соединиться!
Увы, силы муравьев ограничены, так что в конце концов их лапки расцепляются... Два разрыва объединяются в один большой, и это дает резкий толчок дальнейшему растяжению всего ковра.
#популярное #цитаты
Увы, силы муравьев ограничены, так что в конце концов их лапки расцепляются... Два разрыва объединяются в один большой, и это дает резкий толчок дальнейшему растяжению всего ковра.
#популярное #цитаты
😢2😁1😱1
Проблема знака при моделировании квантовых систем методами Монте-Карло возникает из-за того, что различные траектории, по которым производится суммирование для расчета наблюдаемых, могут давать противоположные вклады в результат. В итоге это приводит к большим ошибкам округления и накоплению ошибок, экспоненциально растущих с уменьшением температуры и ростом числа частиц.
В этой работе на примере нескольких моделей продемонстрировано, что обострение проблемы знака может служить признаком близости квантового фазового перехода. На рисунке показаны два примера с моделями Хаббарда на решетке «пчелиные соты». В первом случае (сверху) электроны отталкиваются на узле, а во втором случае (снизу) электроны бесспиновые и отталкиваются на соседних узлах. В обоих случаях видно, что средний знак <S> вкладов траекторий снижается (что свидетельствует о большом числе слагаемых противоположных знаков) вблизи точек квантовых фазовых переходов, отмеченных звездочками.
#квантовая_механика #Монте_Карло
В этой работе на примере нескольких моделей продемонстрировано, что обострение проблемы знака может служить признаком близости квантового фазового перехода. На рисунке показаны два примера с моделями Хаббарда на решетке «пчелиные соты». В первом случае (сверху) электроны отталкиваются на узле, а во втором случае (снизу) электроны бесспиновые и отталкиваются на соседних узлах. В обоих случаях видно, что средний знак <S> вкладов траекторий снижается (что свидетельствует о большом числе слагаемых противоположных знаков) вблизи точек квантовых фазовых переходов, отмеченных звездочками.
#квантовая_механика #Монте_Карло
👍1
А вот тоже интересная модель из статьи из предыдущего поста. Электроны перескакивают по квадратной решетке, отталкиваются на узле с силой U и, вдобавок, подвержены действию внешнего потенциала, имеющего противоположные значения ±Δ на двух подрешетках (это имитирует ионный кристалл).
У этой модели любопытная фазовая диаграмма. При Δ >> U и половинном заполнении образуется изолятор с волной зарядовой плотности (это нижняя часть диаграмм на рисунке), потому что электроны парами заполняют более выгодную по энергии подрешетку с потенциалом –Δ. Повышение U делает такое состояние невыгодным из-за двойных заполнений и при Δ << U (левые части диаграмм) образуется однородный изолятор Мотта-Хаббарда.
В промежутке между двумя изоляторами образуется фаза скоррелированного металла, которая обнаруживается по снижению среднего знака <S>. А два различных по природе изолятора можно отличить по противоположной чувствительности двойных заполнений к возрастанию U (нижняя диаграмма).
#квантовая_механика #сильные_корреляции
У этой модели любопытная фазовая диаграмма. При Δ >> U и половинном заполнении образуется изолятор с волной зарядовой плотности (это нижняя часть диаграмм на рисунке), потому что электроны парами заполняют более выгодную по энергии подрешетку с потенциалом –Δ. Повышение U делает такое состояние невыгодным из-за двойных заполнений и при Δ << U (левые части диаграмм) образуется однородный изолятор Мотта-Хаббарда.
В промежутке между двумя изоляторами образуется фаза скоррелированного металла, которая обнаруживается по снижению среднего знака <S>. А два различных по природе изолятора можно отличить по противоположной чувствительности двойных заполнений к возрастанию U (нижняя диаграмма).
#квантовая_механика #сильные_корреляции
👍1
Кстати, на этом рисунке из предыдущего поста можно заметить, что производная двойных заполнений по U, посчитанная методом Монте-Карло (нижняя диаграмма), в фазе скоррелированного металла ведет себя странно.
Она сильно флуктуирует, от пикселя к пикселю, между положительными и отрицательными значениями. Это и есть проявление проблемы знака: при низких температурах и большом числе частиц накапливаются экспоненциально растущие ошибки, не дающие нормально моделировать систему. Вне фазы скоррелированного металла все считается нормально.
#Монте_Карло
Она сильно флуктуирует, от пикселя к пикселю, между положительными и отрицательными значениями. Это и есть проявление проблемы знака: при низких температурах и большом числе частиц накапливаются экспоненциально растущие ошибки, не дающие нормально моделировать систему. Вне фазы скоррелированного металла все считается нормально.
#Монте_Карло
👍1