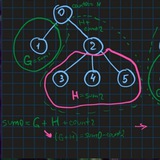
Problem: Find the mode(s) (most frequently occurred element) in a binary search tree with duplicates.

- Input: The root of a binary search tree (BST)
- Output: Array containing the mode(s) of the BST

Assumptions:
- BST has duplicates
- If there are multiple modes, return them in any order

Constraints:
- Number of nodes in the tree: [1, 10^4]
- Node values: -10^5 <= Node.val <= 10^5

Follow-up question: Can you solve this without using any extra space? (Recursion stack does not count)

Problem: The task is to count the number of nodes in a binary tree where the node's value is equal to the average of the values in its subtree.

Example 1:

Input: root = [4,8,5,0,1,null,6]

Output: 5

Explanation:
- For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
- For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
- For the node with value 0: The average of its subtree is 0 / 1 = 0.
- For the node with value 1: The average of its subtree is 1 / 1 = 1.
- For the node with value 6: The average of its subtree is 6 / 1 = 6.

Example 2:

Input: root = [1]

Output: 1

Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.

Constraints:

- The number of nodes in the tree is in the range [1, 1000].
- 0 <= Node.val <= 1000

Problem url: [Build an Array with Stack Operations](https://leetcode.com/problems/build-an-array-with-stack-operations/?envType=daily-question&amp;envId=2023-11-03)

You are given an integer array target and an integer n.
You have an empty stack with the two following operations:
- "Push": pushes an integer to the top of the stack.
- "Pop": removes the integer on the top of the stack.
You also have a stream of the integers in the range [1, n].
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to target. You should follow the following rules:
- If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
- If the stack is not empty, pop the integer at the top of the stack.
- If, at any moment, the elements in the stack (from the bottom to the top) are equal to target, do not read new integers from the stream and do not do more operations on the stack.
Return the stack operations needed to build target following the mentioned rules. If there are multiple valid answers, return any of them.

Example 1:
Input: target = [1,3], n = 3
Output: ["Push","Push","Pop","Push"]
Explanation: Initially the stack s is empty. The last element is the top of the stack.
- Read 1 from the stream and push it to the stack. s = [1].
- Read 2 from the stream and push it to the stack. s = [1,2].
- Pop the integer on the top of the stack. s = [1].
- Read 3 from the stream and push it to the stack. s = [1,3].

Example 2:
Input: target = [1,2,3], n = 3
Output: ["Push","Push","Push"]
Explanation: Initially the stack s is empty. The last element is the top of the stack.
- Read 1 from the stream and push it to the stack. s = [1].
- Read 2 from the stream and push it to the stack. s = [1,2].
- Read 3 from the stream and push it to the stack. s = [1,2,3].

Example 3:
Input: target = [1,2], n = 4
Output: ["Push","Push"]
Explanation: Initially the stack s is empty. The last element is the top of the stack.
- Read 1 from the stream and push it to the stack. s = [1].
- Read 2 from the stream and push it to the stack. s = [1,2].
- Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.

Constraints:
- 1 <= target.length <= 100
- 1 <= n <= 100
- 1 <= target[i] <= n
- target is strictly increasing.

Problem Statement

We have a wooden plank of length *n* units. Ants are walking on the plank, each moving at a speed of 1 unit per second. Some ants move to the left, while others move to the right. When two ants moving in opposite directions meet, they change directions and continue moving. Changing directions does not take any additional time. When an ant reaches one end of the plank, it falls off immediately.

Given the integer *n* and two integer arrays *left* and *right*, which represent the positions of ants moving to the left and right respectively, we need to determine the moment when the last ant(s) fall off the plank.

Example 1:

Input:
- *n* = 4
- *left* = [4,3]
- *right* = [0,1]

Output: 4

Explanation:
- Ant A at index 0 is moving to the right.
- Ant B at index 1 is moving to the right.
- Ant C at index 3 is moving to the left.
- Ant D at index 4 is moving to the left.

The last moment when an ant was on the plank is at time t = 4 seconds. After that, it falls off immediately.

Example 2:

Input:
- *n* = 7
- *left* = []
- *right* = [0,1,2,3,4,5,6,7]

Output: 7

Explanation:
All ants are moving to the right. The ant at index 0 needs 7 seconds to fall off.

Example 3:

Input:
- *n* = 7
- *left* = [0,1,2,3,4,5,6,7]
- *right* = []

Output: 7

Explanation:
All ants are moving to the left. The ant at index 7 needs 7 seconds to fall off.

Constraints:
- 1 <= *n* <= 10^4
- 0 <= *left.length* <= *n* + 1
- 0 <= *left[i]* <= *n*
- 0 <= *right.length* <= *n* + 1
- 0 <= *right[i]* <= *n*
- 1 <= *left.length* + *right.length* <= *n* + 1
- All values of *left* and *right* are unique, and each value can appear only in one of the two arrays.

Yesterday's problem, I accidentally solved another

Problem

[Problem URL](https://leetcode.com/problems/find-the-winner-of-an-array-game/?envType=daily-question&amp;envId=2023-11-05)

Given an integer array arr of distinct integers and an integer k. A game will be played between the first two elements of the array (arr[0] and arr[1]). In each round of the game, we compare arr[0] with arr[1], the larger integer wins and remains at position 0, and the smaller integer moves to the end of the array. The game ends when an integer wins k consecutive rounds. Return the integer which will win the game. It is guaranteed that there will be a winner of the game.

Example 1

Input: arr = [2,1,3,5,4,6,7], k = 2

Output: 5

Explanation: Let's see the rounds of the game:
- Round 1: [2,1,3,5,4,6,7], winner: 2, win count: 1
- Round 2: [2,3,5,4,6,7,1], winner: 3, win count: 1
- Round 3: [3,5,4,6,7,1,2], winner: 5, win count: 1
- Round 4: [5,4,6,7,1,2,3], winner: 5, win count: 2

So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.

Example 2

Input: arr = [3,2,1], k = 10

Output: 3

Explanation: 3 will win the first 10 rounds consecutively.

Constraints

- 2 <= arr.length <= 10^5
- 1 <= arr[i] <= 10^6
- arr contains distinct integers.
- `1 <= k <= 10^9

Problem URL: [https://leetcode.com/problems/seat-reservation-manager/?envType=daily-question&amp;envId=2023-11-06](https://leetcode.com/problems/seat-reservation-manager/?envType=daily-question&amp;envId=2023-11-06)

Text:
Design a system that manages the reservation state of n seats that are numbered from 1 to n.

Implement the SeatManager class:
- SeatManager(int n) Initializes a SeatManager object that will manage n seats numbered from 1 to n. All seats are initially available.
- int reserve() Fetches the smallest-numbered unreserved seat, reserves it, and returns its number.
- void unreserve(int seatNumber) Unreserves the seat with the given seatNumber.

Example:

Input:

["SeatManager", "reserve", "reserve", "unreserve", "reserve", "reserve", "reserve", "reserve", "unreserve"]
[[5], [], [], [2], [], [], [], [], [5]]

Output:

[null, 1, 2, null, 2, 3, 4, 5, null]

Explanation:

SeatManager seatManager = new SeatManager(5); // Initializes a SeatManager with 5 seats.
seatManager.reserve();    // All seats are available, so return the lowest numbered seat, which is 1.
seatManager.reserve();    // The available seats are [2,3,4,5], so return the lowest of them, which is 2.
seatManager.unreserve(2); // Unreserve seat 2, so now the available seats are [2,3,4,5].
seatManager.reserve();    // The available seats are [2,3,4,5], so return the lowest of them, which is 2.
seatManager.reserve();    // The available seats are [3,4,5], so return the lowest of them, which is 3.
seatManager.reserve();    // The available seats are [4,5], so return the lowest of them, which is 4.
seatManager.reserve();    // The only available seat is seat 5, so return 5.
seatManager.unreserve(5); // Unreserve seat 5, so now the available seats are [5].

Constraints:
- 1 <= n <= 10^5
- 1 <= seatNumber <= n
- For each call to reserve, it is guaranteed that there will be at least one unreserved seat.
- For each call to unreserve, it is guaranteed that seatNumber will be reserved.
- At most 10^5 calls in total will be made to reserve and unreserve.

## Problem

You are playing a video game where you are defending your city from a group of n monsters. You are given a 0-indexed integer array dist of size n, where dist[i] is the initial distance in kilometers of the ith monster from the city.

The monsters walk toward the city at a constant speed. The speed of each monster is given to you in an integer array speed of size n, where speed[i] is the speed of the ith monster in kilometers per minute.

You have a weapon that, once fully charged, can eliminate a single monster. However, the weapon takes one minute to charge. The weapon is fully charged at the very start.

You lose when any monster reaches your city. If a monster reaches the city at the exact moment the weapon is fully charged, it counts as a loss, and the game ends before you can use your weapon.

Return the maximum number of monsters that you can eliminate before you lose, or n if you can eliminate all the monsters before they reach the city.

## Example 1

Input: dist = [1,3,4], speed = [1,1,1]
Output: 3
Explanation:
In the beginning, the distances of the monsters are [1,3,4]. You eliminate the first monster.
After a minute, the distances of the monsters are [X,2,3]. You eliminate the second monster.
After a minute, the distances of the monsters are [X,X,2]. You eliminate the thrid monster.
All 3 monsters can be eliminated.

## Example 2

Input: dist = [1,1,2,3], speed = [1,1,1,1]
Output: 1
Explanation:
In the beginning, the distances of the monsters are [1,1,2,3]. You eliminate the first monster.
After a minute, the distances of the monsters are [X,0,1,2], so you lose.
You can only eliminate 1 monster.

## Example 3

Input: dist = [3,2,4], speed = [5,3,2]
Output: 1
Explanation:
In the beginning, the distances of the monsters are [3,2,4]. You eliminate the first monster.
After a minute, the distances of the monsters are [X,0,2], so you lose.
You can only eliminate 1 monster.

## Constraints
- n == dist.length == speed.length
- 1 <= n <= 10^5
- 1 <= dist[i], speed[i] <= 10^5

Problem: Determine if a cell is reachable at a given time

URL: [https://leetcode.com/problems/determine-if-a-cell-is-reachable-at-a-given-time/?envType=daily-question&amp;envId=2023-11-08](https://leetcode.com/problems/determine-if-a-cell-is-reachable-at-a-given-time/?envType=daily-question&amp;envId=2023-11-08)

Text:
You are given four integers sx, sy, fx, fy, and a non-negative integer t.
In an infinite 2D grid, you start at the cell (sx, sy). Each second, you must move to any of its adjacent cells.
Return true if you can reach cell (fx, fy) after exactly t seconds, or false otherwise.
A cell's adjacent cells are the 8 cells around it that share at least one corner with it. You can visit the same cell several times.

Example 1:
Input: sx = 2, sy = 4, fx = 7, fy = 7, t = 6
Output: true
Explanation: Starting at cell (2, 4), we can reach cell (7, 7) in exactly 6 seconds by going through the cells depicted in the picture above.

Example 2:
Input: sx = 3, sy = 1, fx = 7, fy = 3, t = 3
Output: false
Explanation: Starting at cell (3, 1), it takes at least 4 seconds to reach cell (7, 3) by going through the cells depicted in the picture above. Hence, we cannot reach cell (7, 3) at the third second.

Constraints:
- 1 <= sx, sy, fx, fy <= 10^9
- `0 <= t <= 10^9

Problem URL: [https://leetcode.com/problems/count-number-of-homogenous-substrings/?envType=daily-question&amp;envId=2023-11-09](https://leetcode.com/problems/count-number-of-homogenous-substrings/?envType=daily-question&amp;envId=2023-11-09)

Given a string s, return the number of homogenous substrings of s. Modulo 109 + 7 is used for returning the answer, as it may be too large.

A string is homogenous if all its characters are the same. A substring is a contiguous sequence of characters within a string.

Example 1:
Input: s = "abbcccaa"
Output: 13
Explanation: The homogenous substrings are as follows:
- "a" appears 3 times.
- "aa" appears 1 time.
- "b" appears 2 times.
- "bb" appears 1 time.
- "c" appears 3 times.
- "cc" appears 2 times.
- "ccc" appears 1 time.
Total count: 3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.

Example 2:
Input: s = "xy"
Output: 2
Explanation: The homogenous substrings are "x" and "y".

Example 3:
Input: s = "zzzzz"
Output: 15

Constraints:
- 1 <= s.length <= 105
- s consists of lowercase letters.

Problem URL: [https://leetcode.com/problems/restore-the-array-from-adjacent-pairs/?envType=daily-question&amp;envId=2023-11-10](https://leetcode.com/problems/restore-the-array-from-adjacent-pairs/?envType=daily-question&amp;envId=2023-11-10)

Text: There is an integer array nums that consists of n unique elements, but you have forgotten it. However, you do remember every pair of adjacent elements in nums.

You are given a 2D integer array adjacentPairs of size n - 1 where each adjacentPairs[i] = [ui, vi] indicates that the elements ui and vi are adjacent in nums.

It is guaranteed that every adjacent pair of elements nums[i] and nums[i+1] will exist in adjacentPairs, either as [nums[i], nums[i+1]] or [nums[i+1], nums[i]]. The pairs can appear in any order.

Return the original array nums. If there are multiple solutions, return any of them.

Example 1:

Input: adjacentPairs = [[2,1],[3,4],[3,2]]
Output: [1,2,3,4]
Explanation: This array has all its adjacent pairs in adjacentPairs.
Notice that adjacentPairs[i] may not be in left-to-right order.

Example 2:

Input: adjacentPairs = [[4,-2],[1,4],[-3,1]]
Output: [-2,4,1,-3]
Explanation: There can be negative numbers.
Another solution is [-3,1,4,-2], which would also be accepted.

Example 3:

Input: adjacentPairs = [[100000,-100000]]
Output: [100000,-100000]

Constraints:
- nums.length == n
- adjacentPairs.length == n - 1
- adjacentPairs[i].length == 2
- 2 <= n <= 10^5
- -10^5 <= nums[i], ui, vi <= 10^5
- There exists some nums that has adjacentPairs as its pairs.

Problem URL: [Design Graph With Shortest Path Calculator - LeetCode](https://leetcode.com/problems/design-graph-with-shortest-path-calculator/?envType=daily-question&amp;envId=2023-11-11)

Text:
There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [fromi, toi, edgeCosti] meaning that there is an edge from fromi to toi with the cost edgeCosti.

Implement the Graph class:
Graph(int n, int[][] edges) - initializes the object with n nodes and the given edges.
addEdge(int[] edge) - adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.
int shortestPath(int node1, int node2) - returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

Example:

Input
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
Output
[null, 6, -1, null, 6]

Explanation
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6.
g.shortestPath(0, 3); // return -1. There is no path from 0 to 3.
g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above.
g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.

Constraints:
- 1 <= n <= 100
- 0 <= edges.length <= n * (n - 1)
- edges[i].length == edge.length == 3
- 0 <= fromi, toi, from, to, node1, node2 <= n - 1
- 1 <= edgeCosti, edgeCost <= 10^6
- There are no repeated edges and no self-loops in the graph at any point.
- At most 100 calls will be made for addEdge.
- At most 100 calls will be made for shortestPath.

Problem URL: [Bus Routes LeetCode](https://leetcode.com/problems/bus-routes/?envType=daily-question&amp;envId=2023-11-12)

Problem Description: You are given an array routes representing bus routes where routes[i] is a bus route that the i`th bus repeats forever. For example, if `routes[0] = [1, 5, 7], this means that the 0th bus travels in the sequence 1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ... forever.

You will start at the bus stop source (You are not on any bus initially), and you want to go to the bus stop target. You can travel between bus stops by buses only.

Return the least number of buses you must take to travel from source to target. Return -1 if it is not possible.

Examples:

Example 1:

Input: routes = [[1,2,7],[3,6,7]], source = 1, target = 6
Output: 2
Explanation: The best strategy is to take the first bus to the bus stop 7, then take the second bus to the bus stop 6.

Example 2:

Input: routes = [[7,12],[4,5,15],[6],[15,19],[9,12,13]], source = 15, target = 12
Output: -1

Constraints:
- 1 <= routes.length <= 500
- 1 <= routes[i].length <= 105
- All the values of routes[i] are unique.
- sum(routes[i].length) <= 105
- 0 <= routes[i][j] < 106
- 0 <= source, target < 106

Problem Statement:

Given a 0-indexed string s, permute s to get a new string t such that:
1. All consonants remain in their original places. More formally, if there is an index i with 0 <= i < s.length such that s[i] is a consonant, then t[i] = s[i].
2. The vowels must be sorted in the non-decreasing order of their ASCII values. More formally, for pairs of indices i and j with 0 <= i < j < s.length such that s[i] and s[j] are vowels, then t[i] must not have a higher ASCII value than t[j].
Return the resulting string.

The vowels are 'a', 'e', 'i', 'o', and 'u', and they can appear in lowercase or uppercase. Consonants comprise all letters that are not vowels.

Example 1:

Input: s = "lEetcOde"

Output: "lEOtcede"

Explanation: 'E', 'O', and 'e' are the vowels in s; 'l', 't', 'c', and 'd' are all consonants. The vowels are sorted according to their ASCII values, and the consonants remain in the same places.

Example 2:

Input: s = "lYmpH"

Output: "lYmpH"

Explanation: There are no vowels in s (all characters in s are consonants), so we return "lYmpH".

Constraints:

1 <= s.length <= 105

s consists only of letters of the English alphabet in uppercase and lowercase.

[LeetCode Link](https://leetcode.com/problems/sort-vowels-in-a-string/?envType=daily-question&amp;envId=2023-11-13)

Problem url: [https://leetcode.com/problems/unique-length-3-palindromic-subsequences/?envType=daily-question&amp;envId=2023-11-14](https://leetcode.com/problems/unique-length-3-palindromic-subsequences/?envType=daily-question&amp;envId=2023-11-14)

Text: Given a string s, return the number of unique palindromes of length three that are a subsequence of s.

Note that even if there are multiple ways to obtain the same subsequence, it is still only counted once.

A palindrome is a string that reads the same forwards and backwards.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".

Example 1:

Input: s = "aabca"

Output: 3

Explanation: The 3 palindromic subsequences of length 3 are:
- "aba" (subsequence of "aabca")
- "aaa" (subsequence of "aabca")
- "aca" (subsequence of "aabca")

Example 2:

Input: s = "adc"

Output: 0

Explanation: There are no palindromic subsequences of length 3 in "adc".

Example 3:

Input: s = "bbcbaba"

Output: 4

Explanation: The 4 palindromic subsequences of length 3 are:
- "bbb" (subsequence of "bbcbaba")
- "bcb" (subsequence of "bbcbaba")
- "bab" (subsequence of "bbcbaba")
- "aba" (subsequence of "bbcbaba")

Constraints:

- 3 <= s.length <= 105
- s consists of only lowercase English letters.

Today was my 800 problem day anniversary

Problem Statement

You are given an array of positive integers arr. Perform some operations (possibly none) on arr so that it satisfies these conditions:

1. The value of the first element in arr must be 1.
2. The absolute difference between any two adjacent elements must be less than or equal to 1. In other words, abs(arr[i] - arr[i - 1]) <= 1 for each i where 1 <= i < arr.length (0-indexed). abs(x) is the absolute value of x.

There are 2 types of operations that you can perform any number of times:

1. Decrease the value of any element of arr to a smaller positive integer.
2. Rearrange the elements of arr to be in any order.

Return the maximum possible value of an element in arr after performing the operations to satisfy the conditions.

Example 1

Input: arr = [2,2,1,2,1]

Output: 2

Explanation: We can satisfy the conditions by rearranging arr so it becomes [1,2,2,2,1]. The largest element in arr is 2.

Example 2

Input: arr = [100,1,1000]

Output: 3

Explanation: One possible way to satisfy the conditions is by doing the following:

1. Rearrange arr so it becomes [1,100,1000].
2. Decrease the value of the second element to 2.
3. Decrease the value of the third element to 3.

Now arr = [1,2,3], which satisfies the conditions. The largest element in arr is 3.

Example 3

Input: arr = [1,2,3,4,5]

Output: 5

Explanation: The array already satisfies the conditions, and the largest element is 5.

Constraints

1 <= arr.length <= 10^5

1 <= arr[i] <= 10^9

[Problem url](https://leetcode.com/problems/find-unique-binary-string/?envType=daily-question&amp;envId=2023-11-16)

Given an array of strings nums containing n unique binary strings each of length n, return a binary string of length n that does not appear in nums. If there are multiple answers, you may return any of them.

Example 1:

Input: nums = ["01","10"]
Output: "11"

Example 2:

Input: nums = ["00","01"]
Output: "11"

Example 3:

Input: nums = ["111","011","001"]
Output: "101"

Constraints:
- n == nums.length
- 1 <= n <= 16
- nums[i].length == n
- nums[i] is either '0' or '1'.
- All the strings of nums are unique.

Problem Description

Given an array nums of even length n, pair up the elements of nums into n / 2 pairs such that:
- Each element of nums is in exactly one pair, and
- The maximum pair sum is minimized.

Return the minimized maximum pair sum after optimally pairing up the elements.

Example 1:

Input: nums = [3,5,2,3]
Output: 7
Explanation: The elements can be paired up into pairs (3,3) and (5,2).
The maximum pair sum is max(3+3, 5+2) = max(6, 7) = 7.

Example 2:

Input: nums = [3,5,4,2,4,6]
Output: 8
Explanation: The elements can be paired up into pairs (3,5), (4,4), and (6,2).
The maximum pair sum is max(3+5, 4+4, 6+2) = max(8, 8, 8) = 8.

Constraints:

- n == nums.length
- 2 <= n <= 10^5
- n is even.
- 1 <= nums[i] <= 10^5

*Source: [LeetCode](https://leetcode.com/problems/minimize-maximum-pair-sum-in-array/?envType=daily-question&amp;envId=2023-11-17)*

Problem url: [Frequency of the Most Frequent Element - LeetCode](https://leetcode.com/problems/frequency-of-the-most-frequent-element/?envType=daily-question&amp;envId=2023-11-18)

Problem statement:
- Given an integer array nums and an integer k.
- The frequency of an element is the number of times it occurs in the array.
- In one operation, you can choose an index of nums and increment the element at that index by 1.
- Return the maximum possible frequency of an element after performing at most k operations.

Example 1:
- Input: nums = [1,2,4], k = 5
- Output: 3
- Explanation: Increment the first element three times and the second element two times to make nums = [4,4,4]. The element 4 has a frequency of 3.

Example 2:
- Input: nums = [1,4,8,13], k = 5
- Output: 2
- Explanation: There are multiple optimal solutions:
- Increment the first element three times to make nums = [4,4,8,13]. The element 4 has a frequency of 2.
- Increment the second element four times to make nums = [1,8,8,13]. The element 8 has a frequency of 2.
- Increment the third element five times to make nums = [1,4,13,13]. The element 13 has a frequency of 2.

Example 3:
- Input: nums = [3,9,6], k = 2
- Output: 1

Constraints:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
- 1 <= k <= 10^5