Problem url: [https://leetcode.com/problems/majority-element-ii/](https://leetcode.com/problems/majority-element-ii/?envType=daily-question&envId=2023-10-05)
Given an integer array
Example 1:
- 1 <= nums.length <= 5 * 10^4
- -10^9 <= nums[i] <= 10^9
Follow up: Could you solve the problem in linear time and in O(1) space?
Given an integer array
nums of size n, find all elements that appear more than ⌊ n/3 ⌋ times.Example 1:
Input: nums = [3,2,3]Example 2:
Output: [3]
Input: nums = [1]Example 3:
Output: [1]
Input: nums = [1,2]Constraints:
Output: [1,2]
- 1 <= nums.length <= 5 * 10^4
- -10^9 <= nums[i] <= 10^9
Follow up: Could you solve the problem in linear time and in O(1) space?
👍1
Problem: Integer Break
URL: [https://leetcode.com/problems/integer-break/?envType=daily-question&envId=2023-10-06](https://leetcode.com/problems/integer-break/?envType=daily-question&envId=2023-10-06)
Description: Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers. Return the maximum product you can get.
Example 1:
Example 2:
Constraints:
- 2 <= n <= 58
URL: [https://leetcode.com/problems/integer-break/?envType=daily-question&envId=2023-10-06](https://leetcode.com/problems/integer-break/?envType=daily-question&envId=2023-10-06)
Description: Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers. Return the maximum product you can get.
Example 1:
Input: n = 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.
Example 2:
Input: n = 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.
Constraints:
- 2 <= n <= 58
👍1
Problem:
Given three integers
-
- Each element in
- After applying a certain algorithm to
Your goal is to return the number of ways to build
Example:
- Input:
Output:
Explanation: The possible arrays meeting the given conditions are: [1, 1], [2, 1], [2, 2], [3, 1], [3, 2], [3, 3].
- Input:
Output:
Explanation: There are no possible arrays that satisfy the given conditions.
- Input:
Output:
Explanation: The only possible array satisfying the conditions is [1, 1, 1, 1, 1, 1, 1, 1, 1].
Constraints:
- 1 <= n <= 50
- 1 <= m <= 100
- 0 <= k <= n
Given three integers
n, m, and k, you are tasked with building an array arr with the following properties:-
arr consists of exactly n integers.- Each element in
arr is a positive integer between 1 and m.- After applying a certain algorithm to
arr, the resulting search_cost is equal to k.Your goal is to return the number of ways to build
arr satisfying the given conditions. Since the answer may be large, it should be computed modulo 10^9 + 7.Example:
- Input:
n = 2, m = 3, k = 1Output:
6Explanation: The possible arrays meeting the given conditions are: [1, 1], [2, 1], [2, 2], [3, 1], [3, 2], [3, 3].
- Input:
n = 5, m = 2, k = 3Output:
0Explanation: There are no possible arrays that satisfy the given conditions.
- Input:
n = 9, m = 1, k = 1Output:
1Explanation: The only possible array satisfying the conditions is [1, 1, 1, 1, 1, 1, 1, 1, 1].
Constraints:
- 1 <= n <= 50
- 1 <= m <= 100
- 0 <= k <= n
👍1
## Problem
Given two arrays
A subsequence of an array is a new array formed from the original array by deleting some (can be none) of the elements without disturbing the relative positions of the remaining elements.
### Example 1:
Input:
Output:
Explanation: Take subsequence
Their dot product is
### Example 2:
Input:
Output:
Explanation: Take subsequence
Their dot product is
### Example 3:
Input:
Output:
Explanation: Take subsequence
Their dot product is
### Constraints:
-
-
Given two arrays
nums1 and nums2, return the maximum dot product between non-empty subsequences of nums1 and nums2 with the same length.A subsequence of an array is a new array formed from the original array by deleting some (can be none) of the elements without disturbing the relative positions of the remaining elements.
### Example 1:
Input:
nums1 = [2,1,-2,5], nums2 = [3,0,-6] Output:
18 Explanation: Take subsequence
[2,-2] from nums1 and subsequence [3,-6] from nums2. Their dot product is
(2*3 + (-2)*(-6)) = 18.### Example 2:
Input:
nums1 = [3,-2], nums2 = [2,-6,7] Output:
21 Explanation: Take subsequence
[3] from nums1 and subsequence [7] from nums2. Their dot product is
(3*7) = 21.### Example 3:
Input:
nums1 = [-1,-1], nums2 = [1,1] Output:
-1 Explanation: Take subsequence
[-1] from nums1 and subsequence [1] from nums2. Their dot product is
-1.### Constraints:
-
1 <= nums1.length, nums2.length <= 500-
-1000 <= nums1[i], nums2[i] <= 1000👍1
Problem URL: [https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/?envType=daily-question&envId=2023-10-09](https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/?envType=daily-question&envId=2023-10-09)
Text:
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
Example 3:
Input: nums = [], target = 0
Output: [-1,-1]
Constraints:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums is a non-decreasing array.
-109 <= target <= 109
Text:
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
Example 3:
Input: nums = [], target = 0
Output: [-1,-1]
Constraints:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums is a non-decreasing array.
-109 <= target <= 109
👍1
Problem Statement
Given an integer array
- All elements in
- The difference between the maximum element and the minimum element in
For example,
Example 1:
Input:
Output:
Explanation:
Example 2:
Input:
Output:
Explanation: One possible solution is to change the last element to
Example 3:
Input:
Output:
Explanation: One possible solution is to:
- Change the second element to
- Change the third element to
- Change the fourth element to
The resulting array is
Given an integer array
nums, find the minimum number of operations required to make nums continuous. A array is considered continuous if the following conditions are fulfilled:- All elements in
nums are unique.- The difference between the maximum element and the minimum element in
nums equals nums.length - 1.For example,
[4, 2, 5, 3] is continuous, but [1, 2, 3, 5, 6] is not continuous.Example 1:
Input:
nums = [4, 2, 5, 3]Output:
0Explanation:
nums is already continuous.Example 2:
Input:
nums = [1, 2, 3, 5, 6]Output:
1Explanation: One possible solution is to change the last element to
4. The resulting array is [1, 2, 3, 5, 4], which is continuous.Example 3:
Input:
nums = [1, 10, 100, 1000]Output:
3Explanation: One possible solution is to:
- Change the second element to
2.- Change the third element to
3.- Change the fourth element to
4. The resulting array is
[1, 2, 3, 4], which is continuous.👍1
Problem URL: [Number of Flowers in Full Bloom - LeetCode](https://leetcode.com/problems/number-of-flowers-in-full-bloom/?envType=daily-question&envId=2023-10-11)
Problem Description:
You are given a 0-indexed 2D integer array
Return an integer array
Example 1:
Example 2:
Constraints:
- 1 <= flowers.length <= 5 * 10^4
- flowers[i].length == 2
- 1 <= starti <= endi <= 10^9
- 1 <= people.length <= 5 * 10^4
- 1 <= people[i] <= 10^9
Problem Description:
You are given a 0-indexed 2D integer array
flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.Return an integer array
answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.Example 1:
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Example 2:
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Constraints:
- 1 <= flowers.length <= 5 * 10^4
- flowers[i].length == 2
- 1 <= starti <= endi <= 10^9
- 1 <= people.length <= 5 * 10^4
- 1 <= people[i] <= 10^9
❤1👍1
Problem URL: [https://leetcode.com/problems/find-in-mountain-array/?envType=daily-question&envId=2023-10-12](https://leetcode.com/problems/find-in-mountain-array/?envType=daily-question&envId=2023-10-12)
Problem Description:
- An array
-
-
- You cannot access the mountain array directly. You may only access the array using a MountainArray interface:
-
-
- Submissions making more than 100 calls to
Examples:
- Example 1:
-
- Example 2:
-
Constraints:
- 3 <=
- 0 <=
- 0 <=
Problem Description:
- An array
arr is a mountain array if and only if:-
arr.length >= 3
- There exists some i with 0 < i < arr.length - 1 such that:-
arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
- arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
- Given a mountain array mountainArr, return the minimum index such that mountainArr.get(index) == target. If such an index does not exist, return -1.- You cannot access the mountain array directly. You may only access the array using a MountainArray interface:
-
MountainArray.get(k) returns the element of the array at index k (0-indexed).-
MountainArray.length() returns the length of the array.- Submissions making more than 100 calls to
MountainArray.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.Examples:
- Example 1:
-
Input: array = [1,2,3,4,5,3,1], target = 3
- Output: 2
- Explanation: 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.- Example 2:
-
Input: array = [0,1,2,4,2,1], target = 3
- Output: -1
- Explanation: 3 does not exist in the array, so we return -1.Constraints:
- 3 <=
mountain_arr.length() <= 10^4- 0 <=
target <= 10^9- 0 <=
mountain_arr.get(index) <= 10^9👍1
Problem URL: [Min Cost Climbing Stairs](https://leetcode.com/problems/min-cost-climbing-stairs/?envType=daily-question&envId=2023-10-13)
Problem Description:
- Given an integer array
- Once you pay the cost, you can either climb one or two steps.
- You can either start from the step with index 0 or the step with index 1.
- Return the minimum cost to reach the top of the floor.
Example 1:
Example 2:
Constraints:
- 2 <= cost.length <= 1000
- 0 <= cost[i] <= 999
Problem Description:
- Given an integer array
cost where cost[i] is the cost of the ith step on a staircase.- Once you pay the cost, you can either climb one or two steps.
- You can either start from the step with index 0 or the step with index 1.
- Return the minimum cost to reach the top of the floor.
Example 1:
Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.
Example 2:
Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.
Constraints:
- 2 <= cost.length <= 1000
- 0 <= cost[i] <= 999
👍1
Problem description
Given two 0-indexed integer arrays,
1. A paid painter that paints the
2. A free painter that paints any wall in 1 unit of time at a cost of 0. But the free painter can only be used if the paid painter is already occupied.
Return the minimum amount of money required to paint the
Example 1:
Example 2:
Constraints:
- 1 <=
-
- 1 <=
- 1 <=
Given two 0-indexed integer arrays,
cost and time, of size n representing the costs and the time taken to paint n different walls respectively. There are two painters available:1. A paid painter that paints the
ith wall in time[i] units of time and takes cost[i] units of money.2. A free painter that paints any wall in 1 unit of time at a cost of 0. But the free painter can only be used if the paid painter is already occupied.
Return the minimum amount of money required to paint the
n walls.Example 1:
Input: cost = [1,2,3,2], time = [1,2,3,2]
Output: 3
Explanation: The walls at index 0 and 1 will be painted by the paid painter, and it will take 3 units of time; meanwhile, the free painter will paint the walls at index 2 and 3, free of cost in 2 units of time. Thus, the total cost is 1 + 2 = 3.
Example 2:
Input: cost = [2,3,4,2], time = [1,1,1,1]
Output: 4
Explanation: The walls at index 0 and 3 will be painted by the paid painter, and it will take 2 units of time; meanwhile, the free painter will paint the walls at index 1 and 2, free of cost in 2 units of time. Thus, the total cost is 2 + 2 = 4.
Constraints:
- 1 <=
cost.length <= 500-
cost.length == time.length- 1 <=
cost[i] <= 10^6- 1 <=
time[i] <= 500👍1
Problem URL: [Number of Ways to Stay in the Same Place After Some Steps](https://leetcode.com/problems/number-of-ways-to-stay-in-the-same-place-after-some-steps/?envType=daily-question&envId=2023-10-15)
Problem Description:
You have a pointer at index 0 in an array of size
Given two integers
Examples:
- Example 1:
- Input:
- Output:
- Explanation: There are 4 different ways to stay at index 0 after 3 steps.
- Right, Left, Stay
- Stay, Right, Left
- Right, Stay, Left
- Stay, Stay, Stay
- Example 2:
- Input:
- Output:
- Explanation: There are 2 different ways to stay at index 0 after 2 steps.
- Right, Left
- Stay, Stay
- Example 3:
- Input:
- Output:
Constraints:
- 1 <=
- 1 <=
Problem Description:
You have a pointer at index 0 in an array of size
arrLen. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).Given two integers
steps and arrLen, return the number of ways such that your pointer is still at index 0 after exactly steps steps. Since the answer may be too large, return it modulo 10^9 + 7.Examples:
- Example 1:
- Input:
steps = 3, arrLen = 2- Output:
4- Explanation: There are 4 different ways to stay at index 0 after 3 steps.
- Right, Left, Stay
- Stay, Right, Left
- Right, Stay, Left
- Stay, Stay, Stay
- Example 2:
- Input:
steps = 2, arrLen = 4- Output:
2- Explanation: There are 2 different ways to stay at index 0 after 2 steps.
- Right, Left
- Stay, Stay
- Example 3:
- Input:
steps = 4, arrLen = 2- Output:
8Constraints:
- 1 <=
steps <= 500- 1 <=
arrLen <= 10^6👍1
Problem url: [https://leetcode.com/problems/pascals-triangle-ii/?envType=daily-question&envId=2023-10-16](https://leetcode.com/problems/pascals-triangle-ii/?envType=daily-question&envId=2023-10-16)
Text:
Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
Example 1:
Input: rowIndex = 3
Output: [1,3,3,1]
Example 2:
Input: rowIndex = 0
Output: [1]
Example 3:
Input: rowIndex = 1
Output: [1,1]
Constraints:
0 <= rowIndex <= 33
Follow up:
Could you optimize your algorithm to use only O(rowIndex) extra space?
Text:
Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
Example 1:
Input: rowIndex = 3
Output: [1,3,3,1]
Example 2:
Input: rowIndex = 0
Output: [1]
Example 3:
Input: rowIndex = 1
Output: [1,1]
Constraints:
0 <= rowIndex <= 33
Follow up:
Could you optimize your algorithm to use only O(rowIndex) extra space?
👍1
Problem url: [https://leetcode.com/problems/validate-binary-tree-nodes/?envType=daily-question&envId=2023-10-17](https://leetcode.com/problems/validate-binary-tree-nodes/?envType=daily-question&envId=2023-10-17)
You have n binary tree nodes numbered from 0 to n - 1. Each node i has two children leftChild[i] and rightChild[i].
Return true if and only if all the given nodes form exactly one valid binary tree.
If node i has no left child, then leftChild[i] will equal -1. Similarly, if node i has no right child, then rightChild[i] will equal -1.
Note that the nodes have no values and we only use the node numbers in this problem.
Example 1:
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true
Example 2:
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false
Example 3:
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false
Constraints:
- n == leftChild.length == rightChild.length
- 1 <= n <= 10^4
- -1 <= leftChild[i], rightChild[i] <= n - 1
You have n binary tree nodes numbered from 0 to n - 1. Each node i has two children leftChild[i] and rightChild[i].
Return true if and only if all the given nodes form exactly one valid binary tree.
If node i has no left child, then leftChild[i] will equal -1. Similarly, if node i has no right child, then rightChild[i] will equal -1.
Note that the nodes have no values and we only use the node numbers in this problem.
Example 1:
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true
Example 2:
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false
Example 3:
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false
Constraints:
- n == leftChild.length == rightChild.length
- 1 <= n <= 10^4
- -1 <= leftChild[i], rightChild[i] <= n - 1
👍1
Problem Description
You are given an integer
You must find the minimum number of months needed to complete all the courses following these rules:
- You may start taking a course at any time if the prerequisites are met.
- Any number of courses can be taken at the same time.
Return the minimum number of months needed to complete all the courses.
Example 1
Input:
Output:
Explanation:
The given graph and the time required to complete each course:
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
Example 2
Input:
Output:
Explanation:
The given graph and the time required to complete each course:
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
Constraints
- 1 <= n <= 5 * 10^4
- 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)
- relations[j].length == 2
- 1 <= prevCoursej, nextCoursej <= n
- prevCoursej != nextCoursej
- All the pairs [prevCoursej, nextCoursej] are unique.
- time.length == n
- 1 <= time[i] <= 10^4
- The given graph is a directed acyclic graph.
Problem URL: [https://leetcode.com/problems/parallel-courses-iii/?envType=daily-question&envId=2023-10-18](https://leetcode.com/problems/parallel-courses-iii/?envType=daily-question&envId=2023-10-18)
You are given an integer
n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the `(i+1)`th course.You must find the minimum number of months needed to complete all the courses following these rules:
- You may start taking a course at any time if the prerequisites are met.
- Any number of courses can be taken at the same time.
Return the minimum number of months needed to complete all the courses.
Example 1
Input:
python
n = 3,
relations = [[1,3],[2,3]],
time = [3,2,5]
Output:
python
8
Explanation:
The given graph and the time required to complete each course:
1 2 3
______ ______ ______
| | | |
v v v v
3m 2m 5m
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
Example 2
Input:
python
n = 5,
relations = [[1,5],[2,5],[3,5],[3,4],[4,5]],
time = [1,2,3,4,5]
Output:
python
12
Explanation:
The given graph and the time required to complete each course:
/ 1 2 3 4
/______________________________
| | | | |
v v v v v
1m 2m 3m 4m 5m
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
Constraints
- 1 <= n <= 5 * 10^4
- 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)
- relations[j].length == 2
- 1 <= prevCoursej, nextCoursej <= n
- prevCoursej != nextCoursej
- All the pairs [prevCoursej, nextCoursej] are unique.
- time.length == n
- 1 <= time[i] <= 10^4
- The given graph is a directed acyclic graph.
Problem URL: [https://leetcode.com/problems/parallel-courses-iii/?envType=daily-question&envId=2023-10-18](https://leetcode.com/problems/parallel-courses-iii/?envType=daily-question&envId=2023-10-18)
👍2
Problem URL:
[https://leetcode.com/problems/backspace-string-compare/?envType=daily-question&envId=2023-10-19](https://leetcode.com/problems/backspace-string-compare/?envType=daily-question&envId=2023-10-19)
Problem Description:
Given two strings
Note that after backspacing an empty text, the text will continue empty.
Example 1:
Input: s = "ab#c", t = "ad#c"
Output: true
Explanation: Both s and t become "ac".
Example 2:
Input: s = "ab##", t = "c#d#"
Output: true
Explanation: Both s and t become "".
Example 3:
Input: s = "a#c", t = "b"
Output: false
Explanation: s becomes "c" while t becomes "b".
Constraints:
- 1 <= s.length, t.length <= 200
- s and t only contain lowercase letters and '#' characters.
Follow up:
Can you solve it in O(n) time and O(1) space?
[https://leetcode.com/problems/backspace-string-compare/?envType=daily-question&envId=2023-10-19](https://leetcode.com/problems/backspace-string-compare/?envType=daily-question&envId=2023-10-19)
Problem Description:
Given two strings
s and t, return true if they are equal when both are typed into empty text editors. # means a backspace character.Note that after backspacing an empty text, the text will continue empty.
Example 1:
Input: s = "ab#c", t = "ad#c"
Output: true
Explanation: Both s and t become "ac".
Example 2:
Input: s = "ab##", t = "c#d#"
Output: true
Explanation: Both s and t become "".
Example 3:
Input: s = "a#c", t = "b"
Output: false
Explanation: s becomes "c" while t becomes "b".
Constraints:
- 1 <= s.length, t.length <= 200
- s and t only contain lowercase letters and '#' characters.
Follow up:
Can you solve it in O(n) time and O(1) space?
👍1
Problem Description
You are given a nested list of integers
Implement the
-
-
-
Your code will be tested with the following pseudocode:
If
Example 1:
Input:
Output:
Explanation: By calling
Example 2:
Input:
Output:
Explanation: By calling
Constraints:
- 1 <= nestedList.length <= 500
- The values of the integers in the nested list are in the range [-10^6, 10^6].
Problem URL: [Flatten Nested List Iterator](https://leetcode.com/problems/flatten-nested-list-iterator/?envType=daily-question&envId=2023-10-20)
You are given a nested list of integers
nestedList. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.Implement the
NestedIterator class:-
NestedIterator(List<NestedInteger> nestedList): Initializes the iterator with the nested list nestedList.-
int next(): Returns the next integer in the nested list.-
boolean hasNext(): Returns true if there are still some integers in the nested list and false otherwise.Your code will be tested with the following pseudocode:
initialize iterator with nestedList
res = []
while iterator.hasNext()
append iterator.next() to the end of res
return res
If
res matches the expected flattened list, then your code will be judged as correct.Example 1:
Input:
nestedList = [[1,1],2,[1,1]]Output:
[1,1,2,1,1]Explanation: By calling
next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,1,2,1,1].Example 2:
Input:
nestedList = [1,[4,[6]]]Output:
[1,4,6]Explanation: By calling
next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,4,6].Constraints:
- 1 <= nestedList.length <= 500
- The values of the integers in the nested list are in the range [-10^6, 10^6].
Problem URL: [Flatten Nested List Iterator](https://leetcode.com/problems/flatten-nested-list-iterator/?envType=daily-question&envId=2023-10-20)
👍1
Problem URL: [Problem Link](https://leetcode.com/problems/constrained-subsequence-sum/?envType=daily-question&envId=2023-10-21)
Problem Statement:
Given an integer array
A subsequence of an array is obtained by deleting some number of elements (can be zero) from the array, leaving the remaining elements in their original order.
Example 1:
Example 2:
Example 3:
Constraints:
- 1 <= k <= nums.length <= 10^5
- -104 <= nums[i] <= 10^4
Problem Statement:
Given an integer array
nums and an integer k, return the maximum sum of a non-empty subsequence of that array such that for every two consecutive integers in the subsequence, nums[i] and nums[j], where i < j, the condition j - i <= k is satisfied.A subsequence of an array is obtained by deleting some number of elements (can be zero) from the array, leaving the remaining elements in their original order.
Example 1:
Input: nums = [10,2,-10,5,20], k = 2
Output: 37
Explanation: The subsequence is [10, 2, 5, 20].
Example 2:
Input: nums = [-1,-2,-3], k = 1
Output: -1
Explanation: The subsequence must be non-empty, so we choose the largest number.
Example 3:
Input: nums = [10,-2,-10,-5,20], k = 2
Output: 23
Explanation: The subsequence is [10, -2, -5, 20].
Constraints:
- 1 <= k <= nums.length <= 10^5
- -104 <= nums[i] <= 10^4
👍1
[Problem url](https://leetcode.com/problems/maximum-score-of-a-good-subarray/?envType=daily-question&envId=2023-10-22)
You are given an array of integers
The score of a subarray
A good subarray is a subarray where
Return the maximum possible score of a good subarray.
Example 1:
Example 2:
Constraints:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 2 * 10^4
- 0 <= k < nums.length
You are given an array of integers
nums (0-indexed) and an integer k.The score of a subarray
(i, j) is defined as min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1). A good subarray is a subarray where
i <= k <= j.Return the maximum possible score of a good subarray.
Example 1:
Input: nums = [1,4,3,7,4,5], k = 3
Output: 15
Explanation: The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15.
Example 2:
Input: nums = [5,5,4,5,4,1,1,1], k = 0
Output: 20
Explanation: The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) * (4-0+1) = 4 * 5 = 20.
Constraints:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 2 * 10^4
- 0 <= k < nums.length
👍1
[Problem link](https://leetcode.com/problems/power-of-four/?envType=daily-question&envId=2023-10-23)
Given an integer n, return true if it is a power of four. Otherwise, return false.
An integer n is a power of four, if there exists an integer x such that n == 4x.
Example 1:
Input: n = 16
Output: true
Example 2:
Input: n = 5
Output: false
Example 3:
Input: n = 1
Output: true
Constraints:
-231 <= n <= 231 - 1
Follow up: Could you solve it without loops/recursion?
Given an integer n, return true if it is a power of four. Otherwise, return false.
An integer n is a power of four, if there exists an integer x such that n == 4x.
Example 1:
Input: n = 16
Output: true
Example 2:
Input: n = 5
Output: false
Example 3:
Input: n = 1
Output: true
Constraints:
-231 <= n <= 231 - 1
Follow up: Could you solve it without loops/recursion?
👍1
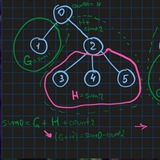
[Problem Statement](https://leetcode.com/problems/find-largest-value-in-each-tree-row/?envType=daily-question&envId=2023-10-24)
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
- Input: root = [1,3,2,5,3,null,9]
- Output: [1,3,9]
Example 2:
- Input: root = [1,2,3]
- Output: [1,3]
Constraints:
- The number of nodes in the tree will be in the range [0, 104].
- -2^31 <= Node.val <= 2^31 - 1
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
- Input: root = [1,3,2,5,3,null,9]
- Output: [1,3,9]
Example 2:
- Input: root = [1,2,3]
- Output: [1,3]
Constraints:
- The number of nodes in the tree will be in the range [0, 104].
- -2^31 <= Node.val <= 2^31 - 1
👍1