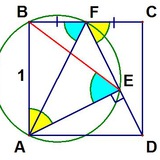
Forwarded from Олимпиадная геометрия
Несколько замечательных свойств одной замечательной точки, у которой пока нет замечательного названия...
несложная задача со вчерашнего выступления Ю.А.Блинкова на семинаре учителей
Forwarded from Олимпиадная геометрия
Всем привет! Самое время для анонса! Почти ровно через две недели 14-го мая в 17:00 по московскому времени мы повторим эксперимент: на нашем канале состоится лекция Павла Витальевича Бибикова, на которой мы обсудим много интересного и нетривиального!
О неожиданных конструкциях в евклидовой геометрии: как коники, инволюции и геометрия Лобачевского помогают понимать задачи классической геометрии.
На лекции будет рассказано о неожиданной связи классической школьной геометрии и конструкциях, которые традиционно считаются весьма далекими от тех, которые знакомы и известны школьникам. Мы начнем с воспоминаний о прошедшем финале ВсОШ и обсудим решения задач 9.4 и 10.4 с помощью прямоугольных гипербол, поговорим о теореме Дезарга об инволюции и ее применении в задаче 11.4, а затем обсудим задачу, предлагавшуюся несколько лет назад участникам сборной России на Международную математическую олимпиаду, для понимания природы которой оказывается полезной геометрия Лобачевского. В ходе лекции будут также поставлены открытые вопросы и проблемы, над которыми можно думать самостоятельно.
Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения). Также будет полезно знание определений конических сечений (эллипс, гипербола, парабола).
О неожиданных конструкциях в евклидовой геометрии: как коники, инволюции и геометрия Лобачевского помогают понимать задачи классической геометрии.
На лекции будет рассказано о неожиданной связи классической школьной геометрии и конструкциях, которые традиционно считаются весьма далекими от тех, которые знакомы и известны школьникам. Мы начнем с воспоминаний о прошедшем финале ВсОШ и обсудим решения задач 9.4 и 10.4 с помощью прямоугольных гипербол, поговорим о теореме Дезарга об инволюции и ее применении в задаче 11.4, а затем обсудим задачу, предлагавшуюся несколько лет назад участникам сборной России на Международную математическую олимпиаду, для понимания природы которой оказывается полезной геометрия Лобачевского. В ходе лекции будут также поставлены открытые вопросы и проблемы, над которыми можно думать самостоятельно.
Для понимания материала будет достаточно знания классических фактов евклидовой геометрии (гомотетия, инверсия) и представление о базовых вещах из геометрии проективной (проективные преобразования, двойные отношения). Также будет полезно знание определений конических сечений (эллипс, гипербола, парабола).
Forwarded from Квантландия | Интересные задачи и не только
Когда я был школьником, то попал на семинар к известному геометру И.Ф. Шарыгину, который заметил, что было бы здОрово привнести в геометрию ещё и цвет. Именно это мы и пытаемся делать! А сегодня такая задачка:
В прямоугольном треугольнике проведена высота. В исходный и в два образовавшихся треугольника вписали круги. Известно, что площади двух луночек на рисунке равны 2 и 3 соответственно. Чему равна площадь зелёной криволинейной фигуры?
Подписаться на телеграм-канал
В прямоугольном треугольнике проведена высота. В исходный и в два образовавшихся треугольника вписали круги. Известно, что площади двух луночек на рисунке равны 2 и 3 соответственно. Чему равна площадь зелёной криволинейной фигуры?
Подписаться на телеграм-канал
Forwarded from Олимпиадная геометрия
Несколько фактов про точку касания полувписанной окружности
Старая моя задача. На самом деле решаемая. Точки P выбираются внутри треугольника ABC так, что сумма зелёных = сумме красных. Точка Q - изогонально сопряжена точке P относительно ABC. Докажите, что PQ проходит через фиксированную точку.