​​Максим Волчкевич опубликовал задачу в подарок Рафаилу Калмановичу Гордину. Вот она:

Дан выпуклый пятиугольник. Из некоторой точки внутри него на все его стороны опустили перпендикуляры. Оказалось, что основания перпендикуляров лежат на одной окружности. Постройте центр этой окружности, если дан только исходный пятиугольник (точка внутри него не известна).

#задача

Семинар в МЦНМО

В этот четверг 22 ноября в 19:00 в МЦНМО.

А.В.Шкловер, Д.Э.Шноль «На пути к дельтоиду» и «Семь новых признаков параллелограмма».
Доклад о двух уроках геометрии восьмого класса.

В первом уроке мы обсудим, как построить урок исследования примеров и контрпримеров, отталкиваясь от ошибок, совершаемых учениками.

Идея второго урока — смешать половинки разных признаков параллелограмма. Признаки параллелограмма состоят из двух частей. Например, две пары противоположных сторон равны. Или: есть две пары равных противоположных углов. Или: обе диагонали делятся точкой пересечения пополам. Но что будет, если смешать половинки разных признаков? Останутся ли они верными?

https://www.mccme.ru/nir/seminar/

Надо было уехать из России, чтобы продолжить писать задачи и их решения. Надо было вернуться, чтобы обнаружить, что Телеграф у трети читателей не открывается, в том числе у меня.

Решение задачи 308 в ВК.

#решение

309. Стороны синего и зеленого правильных треугольников соответственно параллельны. Периметр синего треугольника равен 4, а периметр зеленого треугольника равен 5. Найдите периметр шестиугольника, полученного в пересечении этих треугольников.

#задача

Учителям, которые недавно присоединились

В этом канале есть тесты по разным темам с автоматической проверкой. Ищите по слову «тест».

Это условия заочного этапа олимпиады имени И.Ф.Шарыгина.

Там внутри файла есть все подробности. Кратко: до 1 марта присылайте решения.

От себя добавлю, это очень крутая геометрическая олимпиада.

на http://olympiads.mccme.ru/mmo/okrug/okr18.htm появились условия и решения окружных олимпиад по математике, проходивших только что

вот такая задача, например (9-3):
Придумайте, как разрезать контур квадрата со стороной 1 на четыре части и сложить из этих частей контур треугольника. (Толщины контур не имеет.)

здесь была уже картинка с разрезанием правильного треугольника на 5 равных частей. а вот задача Алексея Заславского с близкими мотивами (Турнир мат. боев им. А.П.Савина, 2016 год):

От квадрата 4×4 отрезали угловую клетку. Разрежьте полученную фигуру на 6 равных частей.
(Части могут состоять из нескольких кусков. Но части должны быть равны: если каждая напечатана на своем прозрачном листе, то любые два листа можно совместить так, чтобы части совпали.)

На Матпразднике-2018 была задача, в которой предлагали придумать фигуру, которую можно составить использую тетрамино любого одного вида.

А после Матпраздника предлагалось подумать, обязательно ли в такой фигуре есть дырка. Теперь это обсуждается на Mathoverflow: https://mathoverflow.net/questions/317172/

разрезание на 6 равных несвязных частей (это нетривиальное решение — но есть и до обидного тривиальное: разрезать каждую клетку на 6 одинаковых вертикальных прямоугольников)

вот еще В.В.Прасолов пишет, что готовится новое издание (исправленное и дополненное) его книги

«Книга называется просто “Задачи по планиметрии”, но задачи там сложные. А на днях, ещё до нового года, должна выйти моя книга “Решение задач повышенной сложности по геометрии”. Там будут задачи попроще.»

​​Алексей Сгибнев продолжает творить чудеса в Геогебре.

Смотрите, у него есть группа с постами и апплетами
Если на входе спросят код, введите TEJ9P

Вот недавний пример:
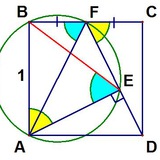
«Коллеги из питерской ФТШ рассказали такую задачу:
Три квадрата фиксированы (см. чертеж), четвёртый подвижен (можно двигать за точку I). Докажите, что площадь жёлтого треугольника не меняется.
Аккуратный компьютерный чертёж отлично помогает догадаться до решения.»
И апплет, где всё это можно пошевелить

Видеозаписи семинара

А.В.Шкловер: https://youtu.be/tRcFYI_krGI
Д.Э.Шноль: https://youtu.be/1vS6o82oyGI

Семинар в МЦНМО

В четверг 27 декабря на новогоднем заседании семинара учителей математики Николай Андреев, Николай Петрович Долбилин и Никита Панюнин будут рассказывать про математическую составляющую изображения мира на плоскости — и про карты, и про картины.

С 19:00, в столовой МЦНМО на 1 этаже.

https://mccme.ru/nir/seminar

​​Калейдоскоп

Два зеркала, поставленные как распахнутая книжка, показывают, как работают калейдоскопы. Отражение зеркала в зеркале снова работает как зеркало.

На сайте математических этюдов новое видео: эти два зеркала крутят и видно, как отражается отрезок.

Этот постер был тут уже год назад, но вдруг у кого-то его нет.