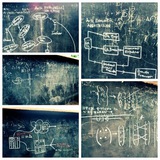
Blackboard Computing Adventures 💡
Photo
Okay.. wait. Seems like we have discovered a new branch of mathematics. But.. fingers crossed. The next paper after introducing Anagram Distance Theory is loading...
#research #foundations #stastistics #informationtheory #informationtransformations #tealanguage #entropy #measures #jwl #phd #nuchwezi @bclectures
#research #foundations #stastistics #informationtheory #informationtransformations #tealanguage #entropy #measures #jwl #phd #nuchwezi @bclectures
Blackboard Computing Adventures 💡
Photo
CHEERS TO ALL MY TEACHERS
Today, I wish to celebrate and commemorate some of my unforgettable teachers and mentors at my higher levels in the not so far past. Some doctors and Professors during those formative years while at #MakerereUniversity. I promise not to disappoint any one of you as I carry forward the work you started in me... 🤞😁📜✍️📚✨✨
#progress #jwl #phd #postgrad #research
Today, I wish to celebrate and commemorate some of my unforgettable teachers and mentors at my higher levels in the not so far past. Some doctors and Professors during those formative years while at #MakerereUniversity. I promise not to disappoint any one of you as I carry forward the work you started in me... 🤞😁📜✍️📚✨✨
#progress #jwl #phd #postgrad #research
Blackboard Computing Adventures 💡
Photo
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio
---[ACM Author]: Joseph Willrich Lutalo, PHd. MSc. BSc. CS,(Phy,Mat) | jwl@nuchwezi.com, joewillrich@gmail.com
---[Preprint Date]: 8 July, 2025
---[Abstract]:
In a recent paper, a new mathematical statistics theory concerning how to quantify changes in entropy across transformations of ordered information expression sequences was introduced, defined and its potential applications across several mathematical science fields illustrated. That measure, the Anagram Distance measure or statistic (ADM), $\tilde{A}(\cdot)$, has since been studied further, and in the process, its inventor has developed three other measures also applicable to the quantification, study and analysis of sequence transformations; the modal sequence statistic (MSS), the transformation compression ratio (TCR) and the piecemeal compression ratio (PCR). These four measures, all of them statistical in nature, have been found to be relevant in the analysis of three families of sequence transformers: anagrammatizers, which only change a sequence's order of members; protractors, which can either increase the cardinality of the post-trasform sequence symbol set or the frequency of some of the members in that set and then compressors, which either eliminate some elements from the post-transform sequence symbol set or reduce their frequency in the resultant sequence --- basically, reversing or the opposite of protraction transforms, and these last two, possibly also involving aspects of the first transform family --- meaning, the order of members in the resultant sequence might likewise be different from that of the input/source sequence. This paper offers the essential introductions to those three transformer families, and the associated entropy and transformation analysis measures and methods proposed for their analysis, with less focus on ADM since it was already well treated in the earlier paper, but otherwise, all this work mostly being developed from scratch --- meaning, there is less reference to any related work or theory there might be concerning this field of inquiry other than the author's, and this paper instead attempts to present original thought and mathematics by the author concerning the matter. These ideas, the mathematics and associated theory, like the earlier work on ADM, would possibly find use in not just mathematical statistics, but also applied statistics such as in bioinformatics, statistical mechanics, artificial intelligence and more. This work is a first attempt at unifying much of the author's work and interests in a kind of basic artificial intelligence founded on the analysis, generation and processing of basic information expressions or rather symbol sequences.
---[ACM Keywords]: Foundations, Ordered Sequences, Entropy Measures, Information Transform Analysis, Statistical Measures, Intelligent Systems, String Processing, Cardinality Measure, Anagram Distance Measure
---[DRAFT-Version]: 1.0.1
---[DRAFT-URI]: https://doi.org/10.6084/m9.figshare.29505824.v1
---[CITE]:
#preprints #acm #acmcs #acmstat #sigstat #sigtrans #mathematicalstastics #transformatics #rngs #phds #universityofoxford
---[ACM Author]: Joseph Willrich Lutalo, PHd. MSc. BSc. CS,(Phy,Mat) | jwl@nuchwezi.com, joewillrich@gmail.com
---[Preprint Date]: 8 July, 2025
---[Abstract]:
In a recent paper, a new mathematical statistics theory concerning how to quantify changes in entropy across transformations of ordered information expression sequences was introduced, defined and its potential applications across several mathematical science fields illustrated. That measure, the Anagram Distance measure or statistic (ADM), $\tilde{A}(\cdot)$, has since been studied further, and in the process, its inventor has developed three other measures also applicable to the quantification, study and analysis of sequence transformations; the modal sequence statistic (MSS), the transformation compression ratio (TCR) and the piecemeal compression ratio (PCR). These four measures, all of them statistical in nature, have been found to be relevant in the analysis of three families of sequence transformers: anagrammatizers, which only change a sequence's order of members; protractors, which can either increase the cardinality of the post-trasform sequence symbol set or the frequency of some of the members in that set and then compressors, which either eliminate some elements from the post-transform sequence symbol set or reduce their frequency in the resultant sequence --- basically, reversing or the opposite of protraction transforms, and these last two, possibly also involving aspects of the first transform family --- meaning, the order of members in the resultant sequence might likewise be different from that of the input/source sequence. This paper offers the essential introductions to those three transformer families, and the associated entropy and transformation analysis measures and methods proposed for their analysis, with less focus on ADM since it was already well treated in the earlier paper, but otherwise, all this work mostly being developed from scratch --- meaning, there is less reference to any related work or theory there might be concerning this field of inquiry other than the author's, and this paper instead attempts to present original thought and mathematics by the author concerning the matter. These ideas, the mathematics and associated theory, like the earlier work on ADM, would possibly find use in not just mathematical statistics, but also applied statistics such as in bioinformatics, statistical mechanics, artificial intelligence and more. This work is a first attempt at unifying much of the author's work and interests in a kind of basic artificial intelligence founded on the analysis, generation and processing of basic information expressions or rather symbol sequences.
---[ACM Keywords]: Foundations, Ordered Sequences, Entropy Measures, Information Transform Analysis, Statistical Measures, Intelligent Systems, String Processing, Cardinality Measure, Anagram Distance Measure
---[DRAFT-Version]: 1.0.1
---[DRAFT-URI]: https://doi.org/10.6084/m9.figshare.29505824.v1
---[CITE]:
Lutalo, Joseph Willrich (2025). The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio. figshare. Online resource. https://doi.org/10.6084/m9.figshare.29505824.v1
#preprints #acm #acmcs #acmstat #sigstat #sigtrans #mathematicalstastics #transformatics #rngs #phds #universityofoxford
figshare
The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors…
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal…
Blackboard Computing Adventures 💡
Photo
POINT of CORRECTION: it is "TRANSFORMERS"
an "R" was missing, but no one noticed 🤷🏻🤦
an "R" was missing, but no one noticed 🤷🏻🤦
Blackboard Computing Adventures 💡
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence…
TRANSFORMATICS_Theory_Of_Sequence_Transformers_10JUL2025_JWL_NuchweziResearch.pdf
4.8 MB
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio
---[ACM Author]: Joseph Willrich Lutalo, PHd. MSc. BSc. CS,(Phy,Mat) | jwl@nuchwezi.com, joewillrich@gmail.com
---[Preprint Date]: 10 July, 2025
---[ACM Author]: Joseph Willrich Lutalo, PHd. MSc. BSc. CS,(Phy,Mat) | jwl@nuchwezi.com, joewillrich@gmail.com
---[Preprint Date]: 10 July, 2025
Blackboard Computing Adventures 💡
TRANSFORMATICS_Theory_Of_Sequence_Transformers_10JUL2025_JWL_NuchweziResearch.pdf
---[ABSTRACT]:
In a recent paper, a new mathematical statistics theory concerning how to quantify changes in entropy across transformations of ordered information expression sequences was introduced, defined and its potential applications across several mathematical science fields illustrated. That measure, the Anagram Distance measure or statistic (ADM), Ã(•), has since been studied further, and in the process, its inventor has developed three other measures also applicable to the quantification, study and analysis of sequence transformations; the modal sequence statistic (MSS), the transformation compression ratio (TCR) and the piecemeal compression ratio (PCR). These four measures, all of them statistical in nature, have been found to be relevant in the analysis of three families of sequence transformers: anagrammatizers, which only change a sequence's order of members; protractors, which can either increase the cardinality of the post-trasform sequence symbol set or the frequency of some of the members in that set and then compressors, which either eliminate some elements from the post-transform sequence symbol set or reduce their frequency in the resultant sequence --- basically, reversing or the opposite of protraction transforms, and these last two, possibly also involving aspects of the first transform family --- meaning, the order of members in the resultant sequence might likewise be different from that of the input/source sequence. This paper offers the essential introductions to those three transformer families, and the associated entropy and transformation analysis measures and methods proposed for their appreciation, with lesser focus on ADM though, since it was already well treated in the earlier paper, but otherwise, all this work mostly being developed from scratch --- meaning, there is less reference to any related work or theory there might be concerning this field of inquiry other than the author's, and this paper instead attempts to present original thought and mathematics by the author concerning the matter. These ideas, the mathematics and associated theory, like the earlier work on ADM, would possibly find use in not just pure mathematical statistics, but also applied statistics such as in bioinformatics, statistical mechanics, statistical artificial intelligence and more. This work is the second (also predominantly mathematical) attempt at unifying much of the author's work and interests in a kind of basic general artificial intelligence platform founded on the generation, processing and analysis of basic information expressions or rather symbol sequences natural or not.
---[Keywords]: Foundations, Transformatics, Artificial Statistical Intelligence, Information Processing, Ordered Sequences, Strings, Symbol Sets, Cardinality, Statistics, Entropy Measures, Sequence Transformer Analysis
---[DRAFT-Version]: 1.1.1
---[DRAFT-URI]: https://doi.org/10.6084/m9.figshare.29505824.v3
---[CITE]:
In a recent paper, a new mathematical statistics theory concerning how to quantify changes in entropy across transformations of ordered information expression sequences was introduced, defined and its potential applications across several mathematical science fields illustrated. That measure, the Anagram Distance measure or statistic (ADM), Ã(•), has since been studied further, and in the process, its inventor has developed three other measures also applicable to the quantification, study and analysis of sequence transformations; the modal sequence statistic (MSS), the transformation compression ratio (TCR) and the piecemeal compression ratio (PCR). These four measures, all of them statistical in nature, have been found to be relevant in the analysis of three families of sequence transformers: anagrammatizers, which only change a sequence's order of members; protractors, which can either increase the cardinality of the post-trasform sequence symbol set or the frequency of some of the members in that set and then compressors, which either eliminate some elements from the post-transform sequence symbol set or reduce their frequency in the resultant sequence --- basically, reversing or the opposite of protraction transforms, and these last two, possibly also involving aspects of the first transform family --- meaning, the order of members in the resultant sequence might likewise be different from that of the input/source sequence. This paper offers the essential introductions to those three transformer families, and the associated entropy and transformation analysis measures and methods proposed for their appreciation, with lesser focus on ADM though, since it was already well treated in the earlier paper, but otherwise, all this work mostly being developed from scratch --- meaning, there is less reference to any related work or theory there might be concerning this field of inquiry other than the author's, and this paper instead attempts to present original thought and mathematics by the author concerning the matter. These ideas, the mathematics and associated theory, like the earlier work on ADM, would possibly find use in not just pure mathematical statistics, but also applied statistics such as in bioinformatics, statistical mechanics, statistical artificial intelligence and more. This work is the second (also predominantly mathematical) attempt at unifying much of the author's work and interests in a kind of basic general artificial intelligence platform founded on the generation, processing and analysis of basic information expressions or rather symbol sequences natural or not.
---[Keywords]: Foundations, Transformatics, Artificial Statistical Intelligence, Information Processing, Ordered Sequences, Strings, Symbol Sets, Cardinality, Statistics, Entropy Measures, Sequence Transformer Analysis
---[DRAFT-Version]: 1.1.1
---[DRAFT-URI]: https://doi.org/10.6084/m9.figshare.29505824.v3
---[CITE]:
Lutalo, Joseph Willrich (2025). The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio. figshare. Online resource. https://doi.org/10.6084/m9.figshare.29505824.v3
figshare
The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors…
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal…
Blackboard Computing Adventures 💡
TRANSFORMATICS_Theory_Of_Sequence_Transformers_10JUL2025_JWL_NuchweziResearch.pdf
#transformatics and being at home in #oxford.. 10JULY2025 ✨🍻 feels like we penned the modern #deadseascrolls
🤞😆
🤞😆
Blackboard Computing Adventures 💡
TRANSFORMATICS_Theory_Of_Sequence_Transformers_10JUL2025_JWL_NuchweziResearch.pdf
Go Read/CITE The Paper:
■■■■■ᓬ□□●□□■■■■■
Lutalo, Joseph Willrich (2025). The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio. figshare. Online Resource. https://doi.org/10.6084/m9.figshare.29505824.v3
■■■■■ᓬ□□●□□■■■■■
---[In Brief]:
A new theory (3 Definitions, 2 Theorems, 11 Transformers and a total of 4 Statistical Measures) applicable to and relating to the matter of analyzing, manipulating and interpreting information sequences and transformations on them using some simple mathematics and algorithms. We have covered a total of 20 sequence transformation scenarios in this single work alone, and have touched on 3 major transformer families — anagrammatizers; that alter a sequence only in the order of its members, protractors; that multiply or grow the source sequence or some of its members, and then compressors: that reduce/summarize a sequence via elimination of some of its members in addition to other possible alterations. This paper proposes and lays the foundations of a new field of scientific & mathematical inquiry we might call TRANSFORMATICS*
---[Keywords]:
Foundations, Transformatics, Artificial Statistical Intelligence, Information Processing, Ordered Sequences, Strings, Symbol Sets, Cardinality, Statistics, Entropy Measures, Sequence Transformer Analysis
*Early reviewers, comments and feedback most welcome ✓
#transformatics #informationtransformers #preprints #acm #acmcs #acmstat #sigstat #sigtrans #mathematicalstatistics #transformers #generators #informationtheory #entropymeasures #rngs #phds #universityofoxford #nuchwezi #profjwl
■■■■■ᓬ□□●□□■■■■■
Lutalo, Joseph Willrich (2025). The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal Sequence Statistic, Transformation Compression Ratio and Piecemeal Compression Ratio. figshare. Online Resource. https://doi.org/10.6084/m9.figshare.29505824.v3
■■■■■ᓬ□□●□□■■■■■
---[In Brief]:
A new theory (3 Definitions, 2 Theorems, 11 Transformers and a total of 4 Statistical Measures) applicable to and relating to the matter of analyzing, manipulating and interpreting information sequences and transformations on them using some simple mathematics and algorithms. We have covered a total of 20 sequence transformation scenarios in this single work alone, and have touched on 3 major transformer families — anagrammatizers; that alter a sequence only in the order of its members, protractors; that multiply or grow the source sequence or some of its members, and then compressors: that reduce/summarize a sequence via elimination of some of its members in addition to other possible alterations. This paper proposes and lays the foundations of a new field of scientific & mathematical inquiry we might call TRANSFORMATICS*
---[Keywords]:
Foundations, Transformatics, Artificial Statistical Intelligence, Information Processing, Ordered Sequences, Strings, Symbol Sets, Cardinality, Statistics, Entropy Measures, Sequence Transformer Analysis
*Early reviewers, comments and feedback most welcome ✓
#transformatics #informationtransformers #preprints #acm #acmcs #acmstat #sigstat #sigtrans #mathematicalstatistics #transformers #generators #informationtheory #entropymeasures #rngs #phds #universityofoxford #nuchwezi #profjwl
figshare
The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors…
---[ACM Preprint]: The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical Measures Applicable to Them: Anagram Distance, Modal…
Blackboard Computing Adventures 💡
Go Read/CITE The Paper: ■■■■■ᓬ□□●□□■■■■■ Lutalo, Joseph Willrich (2025). The Theory of Sequence Transformers & their Statistics: The 3 Information Sequence Transformer Families (Anagrammatizers, Protractors, Compressors) and 4 New and Relevant Statistical…
Further Consequences of Base Symbol-Set Mathematics: what if A-Z was its own base?
QUESTION: So, it looks like, with the idea of arithmetic quantities of numbers based on position within their alphabet, that not only is 1+1 = 2, but a+h=i?
Answer from Inventor of Symbol Set Logic: *That'd be base-26!* Yes, its mathematics somewhat unintuitive given *a* is usually *10* in both base-36 and the more common base-16. But also, "h" as a quantity wouldn't exist in bases lesser than base-18. In which and beyond which, a + h would be "r" not "i". However, a new base with strictly only the letters of the Latin Alphabet would need to account for the quantity zero (0 not letter "O"), and so, perhaps that'd mean setting the first letter in the Alphabet to 0, or rather, that a = 0, b = 1,... , z = 25. In which case, that'd be base-26 or to avoid wars, just base-az proper indeed, and a + h = h or rather generally that:
#symbolsets #positionindices #basearithematics #alphabeticalmath #profjwl #newnumbertheories
QUESTION: So, it looks like, with the idea of arithmetic quantities of numbers based on position within their alphabet, that not only is 1+1 = 2, but a+h=i?
Answer from Inventor of Symbol Set Logic: *That'd be base-26!* Yes, its mathematics somewhat unintuitive given *a* is usually *10* in both base-36 and the more common base-16. But also, "h" as a quantity wouldn't exist in bases lesser than base-18. In which and beyond which, a + h would be "r" not "i". However, a new base with strictly only the letters of the Latin Alphabet would need to account for the quantity zero (0 not letter "O"), and so, perhaps that'd mean setting the first letter in the Alphabet to 0, or rather, that a = 0, b = 1,... , z = 25. In which case, that'd be base-26 or to avoid wars, just base-az proper indeed, and a + h = h or rather generally that:
a + • = • for any • from base-az={a,...,z}#symbolsets #positionindices #basearithematics #alphabeticalmath #profjwl #newnumbertheories
Blackboard Computing Adventures 💡
Further Consequences of Base Symbol-Set Mathematics: what if A-Z was its own base? QUESTION: So, it looks like, with the idea of arithmetic quantities of numbers based on position within their alphabet, that not only is 1+1 = 2, but a+h=i? Answer from Inventor…
Some of the supporting basic calculations... #baseaz #symbolsetlogic #symbolsetarithematic #basearithematic