Forwarded from Алексей
Зародыши мозга в лаборатории проявили спонтанную согласованную активность
У мини-мозга (органоида) зарегистрирована ритмическая электрическая активность.
———
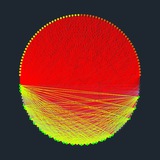
Этой весной из нейронов со стохастическими бинарными синапсами я собрал свой искусственный мини-брэйн, и он так же, спустя некоторое время, затраченное на формирование связей, продемонстрировал ритмическую активность как и его биологический прототип. Причём путём тюнинга можно добиться практически меандра с крутыми фронтами.
Модель представляет собой полносвязную однослойную сеть. Коннектом самостоятельно формируется благодаря спонтанной активности нейронов.
Судя по карте весов, в сети самоорганизуется небольшая группа нейронов, берущих на себя функцию хабов, с которыми имеют слабые связи остальные нейроны.
У мини-мозга (органоида) зарегистрирована ритмическая электрическая активность.
———
Этой весной из нейронов со стохастическими бинарными синапсами я собрал свой искусственный мини-брэйн, и он так же, спустя некоторое время, затраченное на формирование связей, продемонстрировал ритмическую активность как и его биологический прототип. Причём путём тюнинга можно добиться практически меандра с крутыми фронтами.
Модель представляет собой полносвязную однослойную сеть. Коннектом самостоятельно формируется благодаря спонтанной активности нейронов.
Судя по карте весов, в сети самоорганизуется небольшая группа нейронов, берущих на себя функцию хабов, с которыми имеют слабые связи остальные нейроны.
Forwarded from Алексей
Встретился мне в каком-то научпоп фильме эксперимент про иерархию. Стайным животным важно понимать своё и чужое место в иерархии. Эксперимент был, если не ошибаюсь, с гусями, которым демонстрировали разноцветные карточки. Левая половина карточки была закрашена в один цвет, правая в другой. Цвета соответствовали цифрам от 1 до 9 (или больше). Цветовое кодирование выбрано видимо для того, чтобы не обучать их ещё распознаванию чисел.
Обучали гусей поощрением едой при демонстрации и, соответственно, выборе гусем карточки, на которой правое число больше левого. А тестировали их на полном наборе. Через какое-то время гуси начинали выбирать верные карточки чаще случайного выбора. То есть, демонстрировали понимание, что 5 больше 1 и т.п.
Я смоделировал такой механизм. Причём он получился элементарным.
Понятно, что у нас есть две сущности с неким взаимоотношением. Можем представить каждую карточку уникальной парой чисел: 1-2. Соберём из тестового набора направленный граф, где вершинам соответствует числа, а ребро указывает на правое число в паре.
Поиск ответа для пары чисел [A, B], упорядоченной по возрастанию - это поиск пути в графе из вершины A в вершину B. Если путь найден, то порядок верный. That's all, folks!
Результаты
Набор из 10 элементов/чисел. Полное число комбинаций = 100; число комбинаций (a < b) = 45.
1) Доля обучающей выборки 25%. Среднее число попаданий 72%
2) Доля обучающей выборки 50%. Среднее число попаданий 88%
Подобный результат гуси и демонстрировали.
Далее я поиграл с количеством объектов и размером обучающей выборки. Перейду к самому интересному.
Набор из 1000 элементов/чисел. Полное число комбинаций = 1000000; число комбинаций (a < b) = 499500.
Доля обучающей выборки 10%. Среднее число попаданий 97%
Чем больше элементов в иерархии, тем точнее результат и тем меньше требуется обучающая выборка (в процентном отношении).
На один элемент из этого примера выходит примерно по 50 связей. То есть, связность вершин друг с другом довольно низкая, 50 / 1000 = 0.05. Но этого достаточно, чтобы связями сшить куски чего-то заранее неизвестной природы в некий континуум, пространство и затем находить в нём путь.
Для оптимизации поиска пути я применил ранее описанный алгоритм волны. "Глубина" распространения волны поиска оказалась менее 10 переходов. То есть, волна возбуждения прокатывается по цепочке длиной менее 10 вершин/нейронов, чтобы успеть найти путь, или затухнуть, если путь не найден. Такая короткая цепочка нейронов для поиска ответа среди 1000 элементов хорошо соответствует факту о небольшой длине нейронной цепи от сенсорных нейронов до моторных.
Так как элементы/вершины - это абстракция, можно получить такой же обучающий набор (и результаты) для других применений. Если привязать к текущим координатам направления взгляда бинаризованные векторы его смены (влево/вправо и вверх/вниз) в следующую позицию, то просто подвигав глазами десятки тысяч раз, получим две обучающие выборки, аналогичные из примера выше. Один граф станет выдавать пространственное отношение любых двух участков поля зрения по оси X, другой - по оси Y.
Обучали гусей поощрением едой при демонстрации и, соответственно, выборе гусем карточки, на которой правое число больше левого. А тестировали их на полном наборе. Через какое-то время гуси начинали выбирать верные карточки чаще случайного выбора. То есть, демонстрировали понимание, что 5 больше 1 и т.п.
Я смоделировал такой механизм. Причём он получился элементарным.
Понятно, что у нас есть две сущности с неким взаимоотношением. Можем представить каждую карточку уникальной парой чисел: 1-2. Соберём из тестового набора направленный граф, где вершинам соответствует числа, а ребро указывает на правое число в паре.
Поиск ответа для пары чисел [A, B], упорядоченной по возрастанию - это поиск пути в графе из вершины A в вершину B. Если путь найден, то порядок верный. That's all, folks!
Результаты
Набор из 10 элементов/чисел. Полное число комбинаций = 100; число комбинаций (a < b) = 45.
1) Доля обучающей выборки 25%. Среднее число попаданий 72%
2) Доля обучающей выборки 50%. Среднее число попаданий 88%
Подобный результат гуси и демонстрировали.
Далее я поиграл с количеством объектов и размером обучающей выборки. Перейду к самому интересному.
Набор из 1000 элементов/чисел. Полное число комбинаций = 1000000; число комбинаций (a < b) = 499500.
Доля обучающей выборки 10%. Среднее число попаданий 97%
Чем больше элементов в иерархии, тем точнее результат и тем меньше требуется обучающая выборка (в процентном отношении).
На один элемент из этого примера выходит примерно по 50 связей. То есть, связность вершин друг с другом довольно низкая, 50 / 1000 = 0.05. Но этого достаточно, чтобы связями сшить куски чего-то заранее неизвестной природы в некий континуум, пространство и затем находить в нём путь.
Для оптимизации поиска пути я применил ранее описанный алгоритм волны. "Глубина" распространения волны поиска оказалась менее 10 переходов. То есть, волна возбуждения прокатывается по цепочке длиной менее 10 вершин/нейронов, чтобы успеть найти путь, или затухнуть, если путь не найден. Такая короткая цепочка нейронов для поиска ответа среди 1000 элементов хорошо соответствует факту о небольшой длине нейронной цепи от сенсорных нейронов до моторных.
Так как элементы/вершины - это абстракция, можно получить такой же обучающий набор (и результаты) для других применений. Если привязать к текущим координатам направления взгляда бинаризованные векторы его смены (влево/вправо и вверх/вниз) в следующую позицию, то просто подвигав глазами десятки тысяч раз, получим две обучающие выборки, аналогичные из примера выше. Один граф станет выдавать пространственное отношение любых двух участков поля зрения по оси X, другой - по оси Y.
Forwarded from Алексей
Автоматическое разбиение потока слов на слоги частично биоподобным образом
Первичные сенсорные области кодируют пары сигналов: текущий и предыдущий.
* см. ортогональное кодирование сенсорных сигналов
Аналогичным образом разделяем входной поток символов на пересекающиеся пары, и формируем из них поток биграмм.
'пыхтелка'
Входной поток символов:
Собираем статистику по встречаемости каждой биграммы в корпусе текста.
Биграммы можно дополнять триграммами, но из-за более низкой частотности их влияние незначительно.
Первичные сенсорные области кодируют пары сигналов: текущий и предыдущий.
* см. ортогональное кодирование сенсорных сигналов
Аналогичным образом разделяем входной поток символов на пересекающиеся пары, и формируем из них поток биграмм.
'пыхтелка'
Входной поток символов:
[п, ы, х, т, е, л, к, а]Выходной поток биграмм:
[пы, ых, хт, те, ел, лк, ка]Слоги же представляют из себя непересекающиеся последовательности различной длины 2-4.
Собираем статистику по встречаемости каждой биграммы в корпусе текста.
пы 14Каждый символ присутствует в двух соседних биграммах потока. Относим символ к биграмме с большей встречаемостью.
ых 31
хт 3
те 219
ел 236
лк 29
ка 584
п*В результате некоторые биграммы оказываются 'пустыми', на их месте делаем вставку разделителя. После этого сливаем оставшиеся биграммы в выходной поток слогов.
ых
**
т*
ел
**
ка
пых'пых-тел-ка'
тел
ка
Биграммы можно дополнять триграммами, но из-за более низкой частотности их влияние незначительно.
пы 14#syllables
ых 31
хт 3
те 219
ел 236
лк 29
ка 584
пых 1
ыхт 2
хте 1
тел 48
елк 9
лка 8
Forwarded from Алексей
Telegraph
Модель переноса воспоминаний из рабочей памяти в долговременную
Две сети Сеть рабочей памяти и сеть долговременной памяти. Сети связаны друг с другом в одну комплексную сеть. Долговременная память может представлять из себя большую глубокую сеть, обучаемую обратным распространением ошибки. Рабочая память – однослойная…